上海市华东师大松江实验高级中学2024-2025学年高二上学期12月月考数学试卷(PDF版,含答案)
文档属性
| 名称 | 上海市华东师大松江实验高级中学2024-2025学年高二上学期12月月考数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 525.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 07:22:24 | ||
图片预览


文档简介
上海市华东师大松江实验高级中学 2024-2025 学年高二上学期 12 月月
考数学试卷
一、单选题:本题共 4 小题,共 18 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.( + )2 的二项展开式中系数最大的项是( )
A. 第 项 B. 第 + 1项
C. 第 + 1项和第 1项 D. 无法确定
2.4本不同的书分给3人,每人至少1本,共有( )种不同的分法.
A. 36 B. 24 C. 18 D. 72
3.某人将一枚硬币连掷10次,正面朝上的情况出现了8次,若用 表示“正面朝上”这一事件,则 的( )
4 4
A. 概率为 B. 频率为 C. 频率为8 D. 概率接近于8
5 5
4.如果 、 是独立事件, 、 分别是 、 的对立事件,那么以下等式不一定成立的是( )
A. ( ∩ ) = ( ) ( ) B. ( ∩ ) = ( ) ( )
C. ( ∪ ) = ( ) + ( ) D. ( ∩ ) = [1 ( )][1 ( )]
二、填空题:本题共 12 小题,共 54 分。
5.“直线 垂直于平面 内无数条直线”是“ ⊥ ”的______条件.
6.已知圆柱的轴截面是一个边长为4 的正方形,则此圆柱的侧面积为______ 2.
7.已知 = (3, 1,2), 的起点坐标是(2,0, 5),则 的终点坐标为______.
8.由1、2、3、4可以组成______个2在百位的没有重复数字的四位数.
9.二项式(1 2 )11的展开式中所有项的系数之和为______.
1 1
10.在某道路 , 两处设有红灯绿、灯交通信号,汽车在 , 两处通过(即通过绿灯)的概率分别是 和 ,某
3 2
辆汽车在这条道路上匀速行驶,则两处都不停车的概率为______.
11.已知长为3的线段 的两个端点到平面 的距离分别为1和2,则直线 与平面 的所成角大小为______.
12.已知向量 = (0,1, 1), = (1,1,0),若( + ) ⊥ ,则实数 等于______.
13.一个袋子中有2个白球,3个黑球,采用不放回方式从中依次随机地取出2个球,则两次都取到白球的概
率为______.
14.设集合 中的元素皆为无重复数字的二位正整数,且元素中任意两者之积皆为偶数,求集合中元素个数
的最大值______.
第 1 页,共 8 页
15.甲、乙、丙、丁4个人进行乒乓球比赛,首先甲、乙一组,丙、丁一组进行比赛,两组的胜者进入决赛,
决赛的胜者为冠军、败者为亚军. 4个人相互比赛的胜率如表所示,表中的数字表示所在行选手击败其所在
列选手的概率.
甲 乙 丙 丁
甲 — 0.3 0.3 0.8
乙 0.7 — 0.6 0.4
丙 0.7 0.4 — 0.5
丁 0.2 0.6 0.5 —
那么甲得冠军且丙得亚军的概率是______.
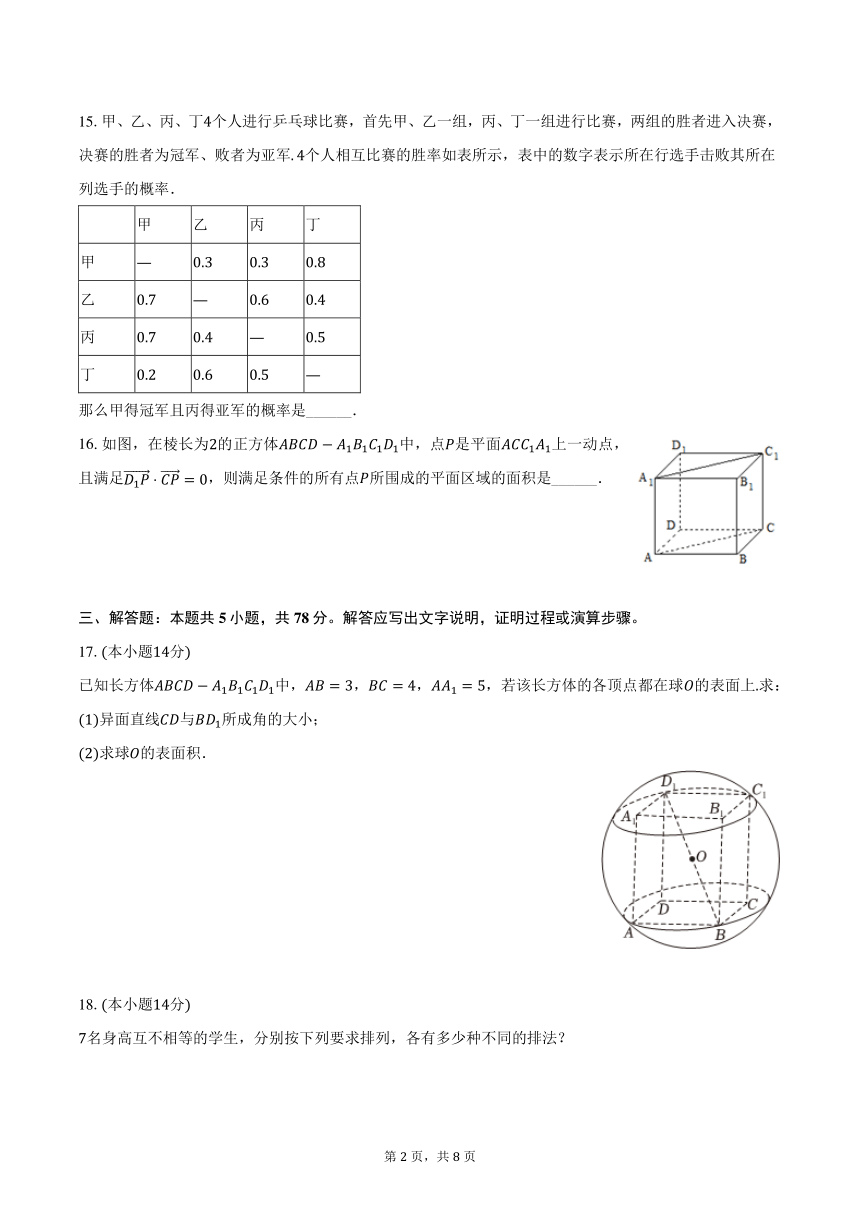
16.如图,在棱长为2的正方体 1 1 1 1中,点 是平面 1 1上一动点,
且满足 1 = 0,则满足条件的所有点 所围成的平面区域的面积是______.
三、解答题:本题共 5 小题,共 78 分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题14分)
已知长方体 1 1 1 1中, = 3, = 4, 1 = 5,若该长方体的各顶点都在球 的表面上.求:
(1)异面直线 与 1所成角的大小;
(2)求球 的表面积.
18.(本小题14分)
7名身高互不相等的学生,分别按下列要求排列,各有多少种不同的排法?
第 2 页,共 8 页
(1)7人站成一排,要求较高的3个学生站在一起;
(2)7人站成一排,要求最高的站在中间,并向左、右两边看,身高逐个递减.
19.(本小题14分)
小明同学参加综合实践活动,设计了一个封闭的包装盒.包装盒如图所示:底面 是边长为8(单位: )
的正方形,△ ,△ ,△ ,△ 均为正三角形,且它们所在的平面都与平面 垂直.
(1)证明: //平面 ;
(2)求该包装盒的容积(不计包装盒材料的厚度).
20.(本小题18分)
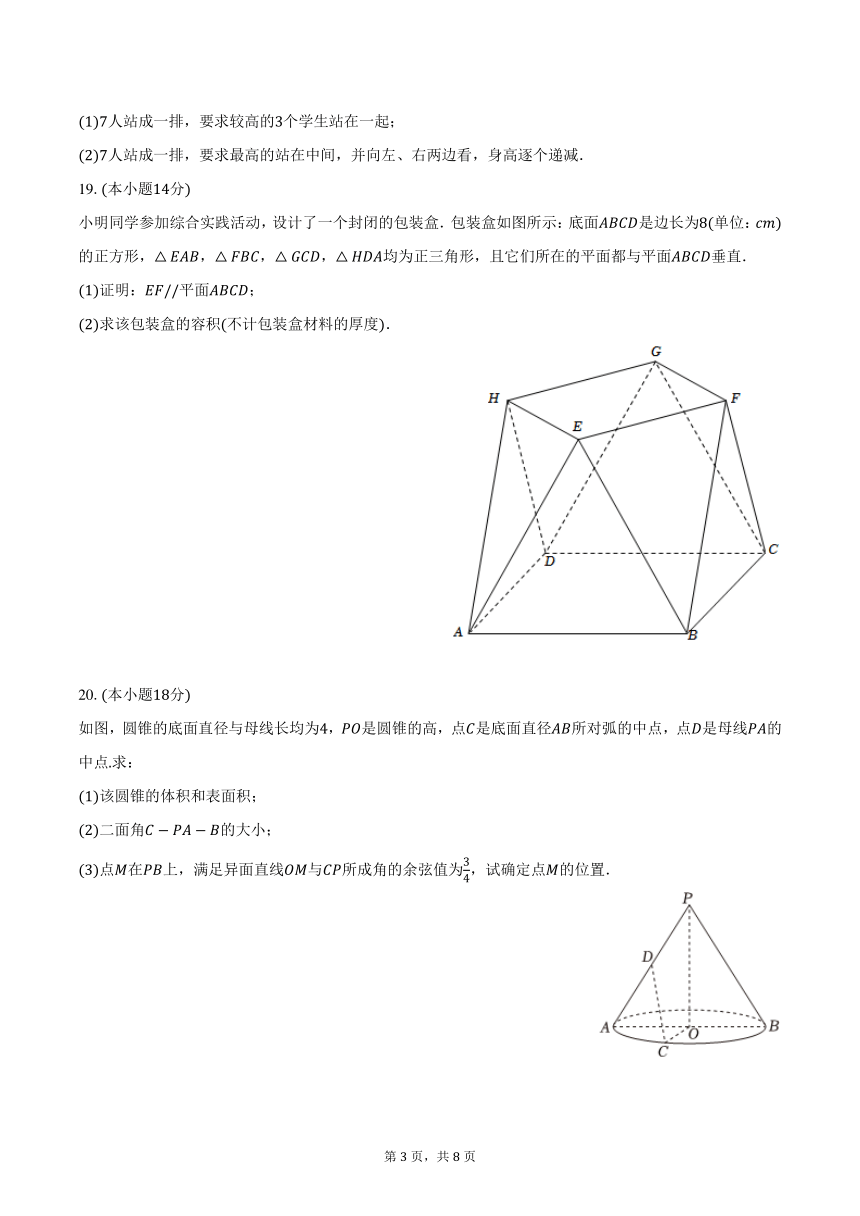
如图,圆锥的底面直径与母线长均为4, 是圆锥的高,点 是底面直径 所对弧的中点,点 是母线 的
中点.求:
(1)该圆锥的体积和表面积;
(2)二面角 的大小;
3
(3)点 在 上,满足异面直线 与 所成角的余弦值为 ,试确定点 的位置.
4
第 3 页,共 8 页
21.(本小题18分)
在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50 以上(含9.50 )的同学将获得
优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单
位: ):
甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;
乙:9.78,9.56,9.51,9.36,9.32,9.23;
丙:9.85,9.65,9.20,9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.
(1)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(2)设 是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,求所有 的可能值及其发生的概率.
(3)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
第 4 页,共 8 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】必要不充分
6.【答案】16
7.【答案】(5, 1, 3)
8.【答案】6
9.【答案】 1
1
10.【答案】
6
1
11.【答案】 或arcsin
2 3
1
12.【答案】
2
1
13.【答案】
10
14.【答案】42
15.【答案】0.045
3
16.【答案】
2
17.【答案】解:(1)根据题意易知 // , ⊥ , = 3, = √ 42 + 521 1 = √ 41,
∴异面直线 与 1所成角∠ 1 ,
√ 41
又tan∠ 1 =
1 = ,
3
√ 41
∴异面直线 与 1所成角的大小为 ; 3
(2)根据题意可得球 的直径2 即为长方体的体对角线长,
∴ (2 )2 = 32 + 42 + 52 = 50,
∴球 的表面积为4 2 = 50 .
18.【答案】解:(1)将较高的3个学生捆成一个元素,与另4个学生构成5个学生自由排列有 55种方法,捆成
一个元素的三学生内部可自由排列,有 33种方法,
所以共有 5 35 3 = 720种;
第 5 页,共 8 页
(2)因为最高的站在中间,
所以从剩余的6名学生中选3名在左边,剩余的3人在右边,
共有 36
3
3 = 20种.
19.【答案】(1)证明:如图所示,将几何体补形为长方体,
做 ′ ⊥ 于点 ′,做 ′ ⊥ 于点 ′,
由于底面为正方形,△ ,△ 均为等边三角形,
故等边三角形的高相等,即 ′ = ′,
由面面垂直的性质可知 ′, ′均与底面垂直,
则 ′// ′,四边形 ′ ′ 为平行四边形,则 // ′ ′,
由于 不在平面 内, ′ ′在平面 内,
由线面平行的判断定理可得 //平面 .
(2)解:易知包装盒的容积为长方体的体积减去四个三棱锥的体积,
其中长方体的高 1 = ′ = 4√ 3,
长方体的体积 1 = 8 × 8 × 4√ 3 = 256√ 3
3,
一个三棱锥的体积 1 1 32√ 3 2 = × ( × 4 × 4) × 4√ 3 =
3,
3 2 3
则包装盒的容积为 32√ 3 640 = 1 4
3
2 = 256√ 3 4 × = √ 3 . 3 3
20.【答案】解:(1)因为圆锥的底面直径与母线长均为4, 是圆锥的高,
所以 = √ 42 22 = 2√ 3,
第 6 页,共 8 页
所以圆锥的体积 1 8√ 3 = × × 22 × 2√ 3 = ,
3 3
1
表面积 = 22 + × 2 × 2 × 4 = 12 ;
2
(2)因为 是圆锥的高,所以 ⊥平面 ,
因为 , 平面 ,所以 ⊥ , ⊥ ,
因为点 是底面直径 所对弧的中点,所以 ⊥ ,
则 , , 两两互相垂直,
则以 为坐标原点, , , 所在直线分别为 , , 轴,建立空间直角坐标系,
则 (0, 2,0), (0,2,0), (2,0,0), (0,0,2√ 3),
所以 = (0,2,2√ 3), = (2,2,0),
设平面 的法向量为 = ( , , ),
= 2 + 2√ 3 = 0
则{ ,令 = √ 3,得 = √ 3, = 1,所以 = ( √ 3, √ 3, 1),
= 2 + 2 = 0
由题知,平面 的一个法向量为 = (1,0,0),
设二面角 的大小为 ,由题知 ∈ (0, ),
2
| | √ 3 √ 21
则 = |cos < , > | = = = ,
| || | √ 7 7
所以二面角 的大小为 √ 21arccos ;
7
(3)因为点 在 上,所以设 = = (0, 2,2√ 3) = (0, 2 , 2√ 3 ),(0 ≤ ≤ 1),
则 = + = (0,2,0) + (0, 2 , 2√ 3 ) = (0,2 2 , 2√ 3 ), = ( 2,0,2√ 3),
3
因为异面直线 与 所成角的余弦值为 ,
4
|cos <
|12 | 3
所以 ,
> | = =
2 2 4,
4×√ (2 2 ) +12
1
解得 = ,所以 为 的中点.
2
第 7 页,共 8 页
21.【答案】解:(1)已知甲以往的9次成绩中有4次获得优秀奖,
若用频率估计概率,
4
则甲在校运动会铅球比赛中获得优秀奖的概率为 ;
9
(2)若用频率估计概率,
3 1
则乙在校运动会铅球比赛中获得优秀奖的概率为 = ,
6 2
2 1
丙在校运动会铅球比赛中获得优秀奖的概率为 = ,
4 2
易知 的所有可能取值为0,1,2,3,
5 1 1 5 5 1 1 4 1 1 7
则 ( = 0) = × × = , ( = 1) = 2 × × × + × × = ,
9 2 2 36 9 2 2 9 2 2 18
5 1 1 4 1 1 13 4 1 1 1
( = 2) = × × + 2 × × × = , ( = 3) = × × = .
9 2 2 9 2 2 36 9 2 2 9
1
(3)由题知乙与丙获得优秀奖的概率较大,均为 ,
2
又丙投出过三人成绩中的最大值9.85 ,在三人中有一定优势,
故如果发挥较好的话丙获得的概率估计值最大.
第 8 页,共 8 页
考数学试卷
一、单选题:本题共 4 小题,共 18 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.( + )2 的二项展开式中系数最大的项是( )
A. 第 项 B. 第 + 1项
C. 第 + 1项和第 1项 D. 无法确定
2.4本不同的书分给3人,每人至少1本,共有( )种不同的分法.
A. 36 B. 24 C. 18 D. 72
3.某人将一枚硬币连掷10次,正面朝上的情况出现了8次,若用 表示“正面朝上”这一事件,则 的( )
4 4
A. 概率为 B. 频率为 C. 频率为8 D. 概率接近于8
5 5
4.如果 、 是独立事件, 、 分别是 、 的对立事件,那么以下等式不一定成立的是( )
A. ( ∩ ) = ( ) ( ) B. ( ∩ ) = ( ) ( )
C. ( ∪ ) = ( ) + ( ) D. ( ∩ ) = [1 ( )][1 ( )]
二、填空题:本题共 12 小题,共 54 分。
5.“直线 垂直于平面 内无数条直线”是“ ⊥ ”的______条件.
6.已知圆柱的轴截面是一个边长为4 的正方形,则此圆柱的侧面积为______ 2.
7.已知 = (3, 1,2), 的起点坐标是(2,0, 5),则 的终点坐标为______.
8.由1、2、3、4可以组成______个2在百位的没有重复数字的四位数.
9.二项式(1 2 )11的展开式中所有项的系数之和为______.
1 1
10.在某道路 , 两处设有红灯绿、灯交通信号,汽车在 , 两处通过(即通过绿灯)的概率分别是 和 ,某
3 2
辆汽车在这条道路上匀速行驶,则两处都不停车的概率为______.
11.已知长为3的线段 的两个端点到平面 的距离分别为1和2,则直线 与平面 的所成角大小为______.
12.已知向量 = (0,1, 1), = (1,1,0),若( + ) ⊥ ,则实数 等于______.
13.一个袋子中有2个白球,3个黑球,采用不放回方式从中依次随机地取出2个球,则两次都取到白球的概
率为______.
14.设集合 中的元素皆为无重复数字的二位正整数,且元素中任意两者之积皆为偶数,求集合中元素个数
的最大值______.
第 1 页,共 8 页
15.甲、乙、丙、丁4个人进行乒乓球比赛,首先甲、乙一组,丙、丁一组进行比赛,两组的胜者进入决赛,
决赛的胜者为冠军、败者为亚军. 4个人相互比赛的胜率如表所示,表中的数字表示所在行选手击败其所在
列选手的概率.
甲 乙 丙 丁
甲 — 0.3 0.3 0.8
乙 0.7 — 0.6 0.4
丙 0.7 0.4 — 0.5
丁 0.2 0.6 0.5 —
那么甲得冠军且丙得亚军的概率是______.
16.如图,在棱长为2的正方体 1 1 1 1中,点 是平面 1 1上一动点,
且满足 1 = 0,则满足条件的所有点 所围成的平面区域的面积是______.
三、解答题:本题共 5 小题,共 78 分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题14分)
已知长方体 1 1 1 1中, = 3, = 4, 1 = 5,若该长方体的各顶点都在球 的表面上.求:
(1)异面直线 与 1所成角的大小;
(2)求球 的表面积.
18.(本小题14分)
7名身高互不相等的学生,分别按下列要求排列,各有多少种不同的排法?
第 2 页,共 8 页
(1)7人站成一排,要求较高的3个学生站在一起;
(2)7人站成一排,要求最高的站在中间,并向左、右两边看,身高逐个递减.
19.(本小题14分)
小明同学参加综合实践活动,设计了一个封闭的包装盒.包装盒如图所示:底面 是边长为8(单位: )
的正方形,△ ,△ ,△ ,△ 均为正三角形,且它们所在的平面都与平面 垂直.
(1)证明: //平面 ;
(2)求该包装盒的容积(不计包装盒材料的厚度).
20.(本小题18分)
如图,圆锥的底面直径与母线长均为4, 是圆锥的高,点 是底面直径 所对弧的中点,点 是母线 的
中点.求:
(1)该圆锥的体积和表面积;
(2)二面角 的大小;
3
(3)点 在 上,满足异面直线 与 所成角的余弦值为 ,试确定点 的位置.
4
第 3 页,共 8 页
21.(本小题18分)
在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50 以上(含9.50 )的同学将获得
优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单
位: ):
甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;
乙:9.78,9.56,9.51,9.36,9.32,9.23;
丙:9.85,9.65,9.20,9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.
(1)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(2)设 是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,求所有 的可能值及其发生的概率.
(3)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
第 4 页,共 8 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】必要不充分
6.【答案】16
7.【答案】(5, 1, 3)
8.【答案】6
9.【答案】 1
1
10.【答案】
6
1
11.【答案】 或arcsin
2 3
1
12.【答案】
2
1
13.【答案】
10
14.【答案】42
15.【答案】0.045
3
16.【答案】
2
17.【答案】解:(1)根据题意易知 // , ⊥ , = 3, = √ 42 + 521 1 = √ 41,
∴异面直线 与 1所成角∠ 1 ,
√ 41
又tan∠ 1 =
1 = ,
3
√ 41
∴异面直线 与 1所成角的大小为 ; 3
(2)根据题意可得球 的直径2 即为长方体的体对角线长,
∴ (2 )2 = 32 + 42 + 52 = 50,
∴球 的表面积为4 2 = 50 .
18.【答案】解:(1)将较高的3个学生捆成一个元素,与另4个学生构成5个学生自由排列有 55种方法,捆成
一个元素的三学生内部可自由排列,有 33种方法,
所以共有 5 35 3 = 720种;
第 5 页,共 8 页
(2)因为最高的站在中间,
所以从剩余的6名学生中选3名在左边,剩余的3人在右边,
共有 36
3
3 = 20种.
19.【答案】(1)证明:如图所示,将几何体补形为长方体,
做 ′ ⊥ 于点 ′,做 ′ ⊥ 于点 ′,
由于底面为正方形,△ ,△ 均为等边三角形,
故等边三角形的高相等,即 ′ = ′,
由面面垂直的性质可知 ′, ′均与底面垂直,
则 ′// ′,四边形 ′ ′ 为平行四边形,则 // ′ ′,
由于 不在平面 内, ′ ′在平面 内,
由线面平行的判断定理可得 //平面 .
(2)解:易知包装盒的容积为长方体的体积减去四个三棱锥的体积,
其中长方体的高 1 = ′ = 4√ 3,
长方体的体积 1 = 8 × 8 × 4√ 3 = 256√ 3
3,
一个三棱锥的体积 1 1 32√ 3 2 = × ( × 4 × 4) × 4√ 3 =
3,
3 2 3
则包装盒的容积为 32√ 3 640 = 1 4
3
2 = 256√ 3 4 × = √ 3 . 3 3
20.【答案】解:(1)因为圆锥的底面直径与母线长均为4, 是圆锥的高,
所以 = √ 42 22 = 2√ 3,
第 6 页,共 8 页
所以圆锥的体积 1 8√ 3 = × × 22 × 2√ 3 = ,
3 3
1
表面积 = 22 + × 2 × 2 × 4 = 12 ;
2
(2)因为 是圆锥的高,所以 ⊥平面 ,
因为 , 平面 ,所以 ⊥ , ⊥ ,
因为点 是底面直径 所对弧的中点,所以 ⊥ ,
则 , , 两两互相垂直,
则以 为坐标原点, , , 所在直线分别为 , , 轴,建立空间直角坐标系,
则 (0, 2,0), (0,2,0), (2,0,0), (0,0,2√ 3),
所以 = (0,2,2√ 3), = (2,2,0),
设平面 的法向量为 = ( , , ),
= 2 + 2√ 3 = 0
则{ ,令 = √ 3,得 = √ 3, = 1,所以 = ( √ 3, √ 3, 1),
= 2 + 2 = 0
由题知,平面 的一个法向量为 = (1,0,0),
设二面角 的大小为 ,由题知 ∈ (0, ),
2
| | √ 3 √ 21
则 = |cos < , > | = = = ,
| || | √ 7 7
所以二面角 的大小为 √ 21arccos ;
7
(3)因为点 在 上,所以设 = = (0, 2,2√ 3) = (0, 2 , 2√ 3 ),(0 ≤ ≤ 1),
则 = + = (0,2,0) + (0, 2 , 2√ 3 ) = (0,2 2 , 2√ 3 ), = ( 2,0,2√ 3),
3
因为异面直线 与 所成角的余弦值为 ,
4
|cos <
|12 | 3
所以 ,
> | = =
2 2 4,
4×√ (2 2 ) +12
1
解得 = ,所以 为 的中点.
2
第 7 页,共 8 页
21.【答案】解:(1)已知甲以往的9次成绩中有4次获得优秀奖,
若用频率估计概率,
4
则甲在校运动会铅球比赛中获得优秀奖的概率为 ;
9
(2)若用频率估计概率,
3 1
则乙在校运动会铅球比赛中获得优秀奖的概率为 = ,
6 2
2 1
丙在校运动会铅球比赛中获得优秀奖的概率为 = ,
4 2
易知 的所有可能取值为0,1,2,3,
5 1 1 5 5 1 1 4 1 1 7
则 ( = 0) = × × = , ( = 1) = 2 × × × + × × = ,
9 2 2 36 9 2 2 9 2 2 18
5 1 1 4 1 1 13 4 1 1 1
( = 2) = × × + 2 × × × = , ( = 3) = × × = .
9 2 2 9 2 2 36 9 2 2 9
1
(3)由题知乙与丙获得优秀奖的概率较大,均为 ,
2
又丙投出过三人成绩中的最大值9.85 ,在三人中有一定优势,
故如果发挥较好的话丙获得的概率估计值最大.
第 8 页,共 8 页
同课章节目录
