第5章 阶段性测验 5.1~5.3.2限时训练(含解析)-2024-2025学年高二下学期数学苏教版(2019) 选择性必修第一册
文档属性
| 名称 | 第5章 阶段性测验 5.1~5.3.2限时训练(含解析)-2024-2025学年高二下学期数学苏教版(2019) 选择性必修第一册 |
|
|
| 格式 | docx | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览



文档简介
阶段性测验 5.1~5.3.2
[分值:100分]
一、单项选择题(每小题5分,共30分)
1.某物体的运动方程为s=5-2t2,则该物体在时间[1,2]上的平均速度为( )
A.-6 B.2 C.-2 D.6
2.已知函数f(x)的导函数为f′(x),且f′(1)=-1,则等于( )
A.-1 B.-3 C.-2 D.-
3.已知函数f(x)=x3-4x,则f(x)的极大值点为( )
A.x=-4 B.x=4 C.x=-2 D.x=2
4.若函数f(x)在R上可导,且f(x)=x2+2f′(2)x+m(m∈R),则( )
A.f(0)C.f(0)>f(5) D.以上答案都不对
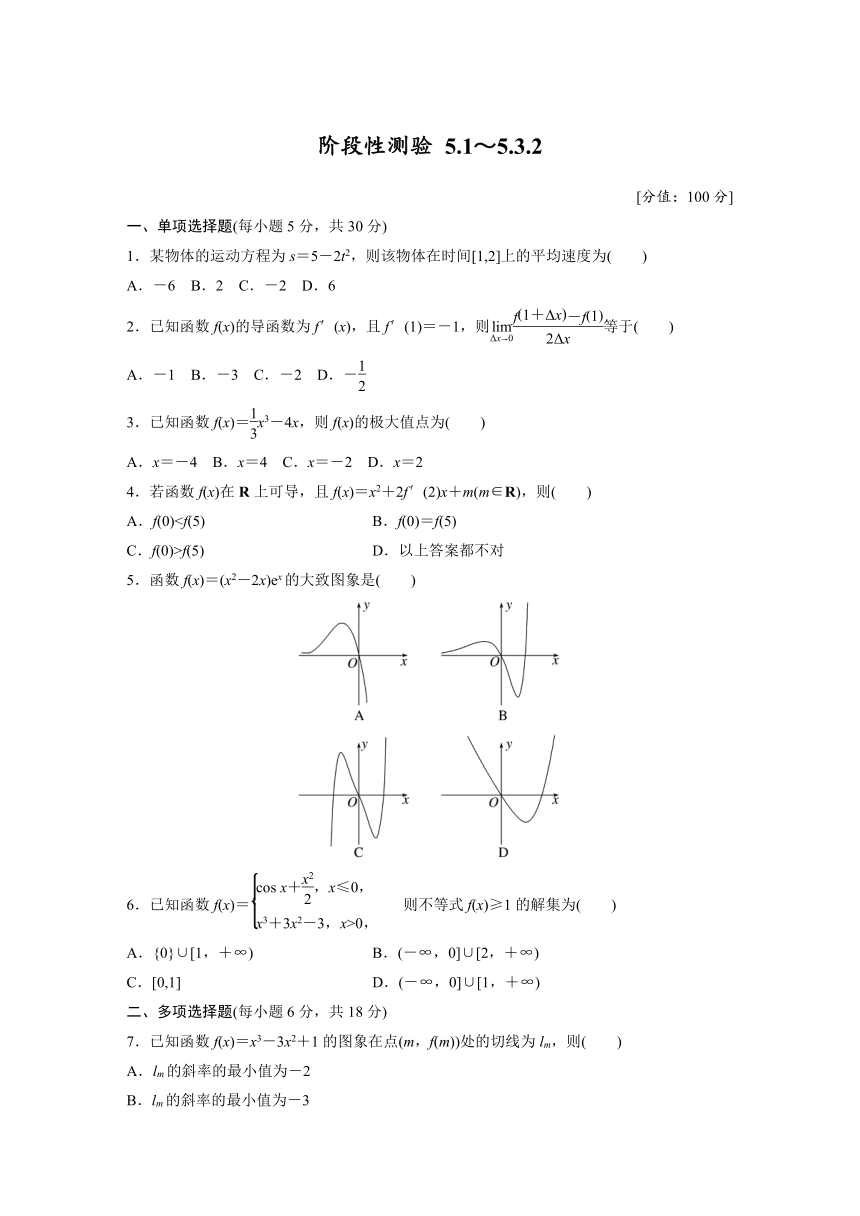
5.函数f(x)=(x2-2x)ex的大致图象是( )
6.已知函数f(x)=则不等式f(x)≥1的解集为( )
A.{0}∪[1,+∞) B.(-∞,0]∪[2,+∞)
C.[0,1] D.(-∞,0]∪[1,+∞)
二、多项选择题(每小题6分,共18分)
7.已知函数f(x)=x3-3x2+1的图象在点(m,f(m))处的切线为lm,则( )
A.lm的斜率的最小值为-2
B.lm的斜率的最小值为-3
C.l0的方程为y=1
D.l-1的方程为y=9x+6
8.函数f(x)=ax3-bx2+cx的图象如图所示,且f(x)在x=-1与x=x0处取得极值,则下列结论正确的有( )
A.a<0
B.c<0
C.f(-1)+f(1)>0
D.函数f′(x)在区间(-∞,0)上单调递减
9.如果对定义在R上的函数y=f(x),对任意两个不相等的实数x1,x2,都有x1f+x2f>x1f+x2f,则称函数y=f(x)为“H函数”,则下列函数是H函数的是( )
A.f(x)=3x-sin x
B.f(x)=
C.f(x)=x3+3x
D.f(x)=ex+x
三、填空题(每小题5分,共15分)
10.已知函数f(x)=2x,若f(x)在x=x0处的导数f′=ln 4,则x0=______.
11.函数f(x)的定义域为开区间,导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有______个极小值点.
12.若函数f(x)=(-x2+ax)ex在区间(-1,1)上存在减区间,则实数a的取值范围是______.
四、解答题(共37分)
13.(12分)已知曲线f(x)=x3-x,求
(1)曲线在点(-1,0)处的切线方程;(3分)
(2)曲线过点(-1,0)的切线方程;(5分)
(3)曲线平行于直线11x-y+1=0的切线方程.(4分)
14.(12分)试求函数f(x)=kx-ln x的单调区间.
15.(13分)已知函数f(x)=-,g(x)=xln x-x2-x.
(1)求f(x)的极值;(4分)
(2)若x∈(1,+∞)时,f(x)与g(x)的单调性相同,求a的取值范围.(9分)
1.A [平均速度为==-6.]
2.D [由导数定义和f′=-1,
得==-.]
3.C [由f(x)=x3-4x,
得f′(x)=x2-4.
令f′(x)=x2-4>0,得x<-2或x>2.
令f′(x)=x2-4<0,得-2所以函数f(x)的增区间为,.函数f(x)的减区间为.
所以x=-2是函数的极大值点,x=2是函数的极小值点.]
4.C [∵f(x)=x2+2f′x+m,
∴f′(x)=2x+2f′,
∴f′=2×2+2f′,
∴f′=-4,
∴f(x)=x2-8x+m,
图象为开口向上的抛物线,其对称轴方程为x=4,
∴f>f.]
5.B [f′(x)=ex+ex=ex,
令f′(x)>0,解得x>或x<-,
令f′(x)<0,解得-所以f(x)=ex在区间上单调递增,在区间上单调递减,在区间上单调递增,所以f(x)的两个极值点为±,故排除选项A和选项D;
当x<0时,x2-2x>0,ex>0,所以f(x)=ex恒为正,排除选项C;
即只有选项B符合要求.]
6.D [当x≤0时,f(x)=cos x+,
求导得f′(x)=-sin x+x,
令h(x)=x-sin x,x≤0,
求导得h′(x)=1-cos x≥0,
则函数h(x),即f′(x)在(-∞,0]上单调递增,
f′(x)≤f′(0)=0,
函数f(x)在(-∞,0]上单调递减,
而f(0)=1,当x≤0时,不等式f(x)≥1 f(x)≥f(0),因此x≤0;
当x>0时,f(x)=x3+3x2-3=(x-1)(x+2)2+1,
由f(x)≥1,得(x-1)(x+2)2≥0,因此x≥1,
所以不等式f(x)≥1的解集为(-∞,0]∪[1,+∞).]
7.BCD [因为f′(x)=3x2-6x=3(x-1)2-3≥-3,所以lm的斜率的最小值为-3,A错误,B正确;
因为f′(0)=0,f(0)=1,所以l0的方程为y=1,C正确;
因为f′(-1)=9,f(-1)=-3,所以l-1的方程为y+3=9(x+1),即y=9x+6,D正确.]
8.BC [因为f(x)=ax3-bx2+cx,
所以f′(x)=3ax2-2bx+c,
由题图知f(x)的增区间是(-∞,-1),,减区间是(-1,x0),所以f′(x)>0的解集为(-∞,-1)∪,
f′(x)<0的解集为(-1,x0),所以a>0,A错误;
因为f(x)在x=-1与x=x0处取得极值,则-1,x0是方程3ax2-2bx+c=0的根,
由根与系数的关系可知=-x0<0 c<0,B正确;
由图可知x0<1 x0-1<0,
由根与系数的关系可知x0-1=<0,故b<0,
故f(-1)+f(1)=-2b>0,C正确;
因为f′(x)=3ax2-2bx+c的图象是开口向上的抛物线,对称轴方程为x==<0,
所以f′(x)在区间上单调递减,在区间上单调递增,D错误.]
9.ACD [对任意两个不相等的实数x1,x2,都有x1f+x2f>x1f+x2f恒成立,
所以不等式等价于(x1-x2)[f(x1)-f(x2)]>0恒成立,
即函数f(x)是增函数,
对于A,函数f(x)=3x-sin x,可得f′(x)=3-cos x>0,
函数f(x)是增函数,符合题意;
对于B,函数f(x)=当x>0时,函数y=ln x单调递增,
当x<0时,函数y=ln(-x)单调递减,不符合题意;
对于C,由函数f(x)=x3+3x,可得f′(x)=3x2+3>0,可得f(x)是增函数,符合题意;
对于D,函数f(x)=ex+x,
可得f′(x)=ex+1>0,
可得f(x)是增函数,符合题意.]
10.1
解析 因为f(x)=2x,所以f′(x)=2xln 2,
又f′=ln 4,所以=ln 4=2ln 2,解得x0=1.
11.1
解析 从导函数的图象上可得导数的零点有4个,
其中满足零点左侧附近导数小于零且右侧附近导数大于零的零点有1个.
12.
解析 f(x)=(-x2+ax)ex,
则f′(x)=ex,
函数f(x)=(-x2+ax)ex在区间(-1,1)上存在减区间,只需-x2+ax-2x+a<0在区间上有解.
记g(x)=-x2+x+a,其对称轴为直线x=,开口向下,g=-1-+a=1>0,只需g<0,
所以-1+a-2+a<0,解得a<.
13.解 (1)由f(x)=x3-x得f′(x)=3x2-1,
则f′(-1)=3-1=2,
所以曲线在点(-1,0)处的切线方程为y=2(x+1),即y=2x+2.
(2)设切点为(x0,x-x0),
则f′(x0)=3x-1,
则切线方程为y=(3x-1)(x-x0)+x-x0,
因为切线过点(-1,0),代入切线方程得,
0=(3x-1)(-1-x0)+x-x0,化简得2x+3x-1=0,
则(x0+1)2(2x0-1)=0 x0=-1或x0=,
所以曲线过点(-1,0)的切线方程为
y=2x+2或y=-x-.
(3)直线11x-y+1=0的斜率为11,
设切点为(x1,x-x1),则f′(x1)=3x-1,
则切线方程为y=(3x-1)(x-x1)+x-x1,
则由切线与直线11x-y+1=0平行得3x-1=11 x=4,
即x1=2或x1=-2,
所以切线方程为y=11x-16或y=11x+16.
14.解 函数f(x)=kx-ln x的定义域为(0,+∞),
f′(x)=k-=.
当k≤0时,kx-1<0,∴f′(x)<0,
则f(x)是减函数.
当k>0时,由f′(x)<0,即<0,
解得0由f′(x)>0,即>0,解得x>.
∴当k>0时,f(x)在区间上单调递减,
在区间上单调递增.
综上所述,当k≤0时,f(x)的减区间为(0,+∞),无增区间;
当k>0时,f(x)的减区间为,增区间为.
15.解 (1)f(x)的定义域为R,f′(x)=,
当x∈(-∞,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,所以f(x)在区间(-∞,1)上单调递减,在区间(1,+∞)上单调递增.
所以f(x)有极小值f(1)=,无极大值.
(2)由(1)知,f(x)在区间(1,+∞)上单调递增.
则g(x)在区间(1,+∞)上单调递增,即g′(x)=1+ln x-ax-1=ln x-ax≥0在(1,+∞)上恒成立,即a≤在(1,+∞)上恒成立,
令p(x)=,x∈(1,+∞),则p′(x)=,
所以当x∈(1,e)时,p′(x)>0;当x∈(e,+∞)时,p′(x)<0,
所以p(x)在区间(1,e)上单调递增,在区间(e,+∞)上单调递减,又x∈(1,+∞)时,p(x)>0,所以p(x)∈,所以a≤0.
[分值:100分]
一、单项选择题(每小题5分,共30分)
1.某物体的运动方程为s=5-2t2,则该物体在时间[1,2]上的平均速度为( )
A.-6 B.2 C.-2 D.6
2.已知函数f(x)的导函数为f′(x),且f′(1)=-1,则等于( )
A.-1 B.-3 C.-2 D.-
3.已知函数f(x)=x3-4x,则f(x)的极大值点为( )
A.x=-4 B.x=4 C.x=-2 D.x=2
4.若函数f(x)在R上可导,且f(x)=x2+2f′(2)x+m(m∈R),则( )
A.f(0)
5.函数f(x)=(x2-2x)ex的大致图象是( )
6.已知函数f(x)=则不等式f(x)≥1的解集为( )
A.{0}∪[1,+∞) B.(-∞,0]∪[2,+∞)
C.[0,1] D.(-∞,0]∪[1,+∞)
二、多项选择题(每小题6分,共18分)
7.已知函数f(x)=x3-3x2+1的图象在点(m,f(m))处的切线为lm,则( )
A.lm的斜率的最小值为-2
B.lm的斜率的最小值为-3
C.l0的方程为y=1
D.l-1的方程为y=9x+6
8.函数f(x)=ax3-bx2+cx的图象如图所示,且f(x)在x=-1与x=x0处取得极值,则下列结论正确的有( )
A.a<0
B.c<0
C.f(-1)+f(1)>0
D.函数f′(x)在区间(-∞,0)上单调递减
9.如果对定义在R上的函数y=f(x),对任意两个不相等的实数x1,x2,都有x1f+x2f>x1f+x2f,则称函数y=f(x)为“H函数”,则下列函数是H函数的是( )
A.f(x)=3x-sin x
B.f(x)=
C.f(x)=x3+3x
D.f(x)=ex+x
三、填空题(每小题5分,共15分)
10.已知函数f(x)=2x,若f(x)在x=x0处的导数f′=ln 4,则x0=______.
11.函数f(x)的定义域为开区间,导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有______个极小值点.
12.若函数f(x)=(-x2+ax)ex在区间(-1,1)上存在减区间,则实数a的取值范围是______.
四、解答题(共37分)
13.(12分)已知曲线f(x)=x3-x,求
(1)曲线在点(-1,0)处的切线方程;(3分)
(2)曲线过点(-1,0)的切线方程;(5分)
(3)曲线平行于直线11x-y+1=0的切线方程.(4分)
14.(12分)试求函数f(x)=kx-ln x的单调区间.
15.(13分)已知函数f(x)=-,g(x)=xln x-x2-x.
(1)求f(x)的极值;(4分)
(2)若x∈(1,+∞)时,f(x)与g(x)的单调性相同,求a的取值范围.(9分)
1.A [平均速度为==-6.]
2.D [由导数定义和f′=-1,
得==-.]
3.C [由f(x)=x3-4x,
得f′(x)=x2-4.
令f′(x)=x2-4>0,得x<-2或x>2.
令f′(x)=x2-4<0,得-2
所以x=-2是函数的极大值点,x=2是函数的极小值点.]
4.C [∵f(x)=x2+2f′x+m,
∴f′(x)=2x+2f′,
∴f′=2×2+2f′,
∴f′=-4,
∴f(x)=x2-8x+m,
图象为开口向上的抛物线,其对称轴方程为x=4,
∴f>f.]
5.B [f′(x)=ex+ex=ex,
令f′(x)>0,解得x>或x<-,
令f′(x)<0,解得-
当x<0时,x2-2x>0,ex>0,所以f(x)=ex恒为正,排除选项C;
即只有选项B符合要求.]
6.D [当x≤0时,f(x)=cos x+,
求导得f′(x)=-sin x+x,
令h(x)=x-sin x,x≤0,
求导得h′(x)=1-cos x≥0,
则函数h(x),即f′(x)在(-∞,0]上单调递增,
f′(x)≤f′(0)=0,
函数f(x)在(-∞,0]上单调递减,
而f(0)=1,当x≤0时,不等式f(x)≥1 f(x)≥f(0),因此x≤0;
当x>0时,f(x)=x3+3x2-3=(x-1)(x+2)2+1,
由f(x)≥1,得(x-1)(x+2)2≥0,因此x≥1,
所以不等式f(x)≥1的解集为(-∞,0]∪[1,+∞).]
7.BCD [因为f′(x)=3x2-6x=3(x-1)2-3≥-3,所以lm的斜率的最小值为-3,A错误,B正确;
因为f′(0)=0,f(0)=1,所以l0的方程为y=1,C正确;
因为f′(-1)=9,f(-1)=-3,所以l-1的方程为y+3=9(x+1),即y=9x+6,D正确.]
8.BC [因为f(x)=ax3-bx2+cx,
所以f′(x)=3ax2-2bx+c,
由题图知f(x)的增区间是(-∞,-1),,减区间是(-1,x0),所以f′(x)>0的解集为(-∞,-1)∪,
f′(x)<0的解集为(-1,x0),所以a>0,A错误;
因为f(x)在x=-1与x=x0处取得极值,则-1,x0是方程3ax2-2bx+c=0的根,
由根与系数的关系可知=-x0<0 c<0,B正确;
由图可知x0<1 x0-1<0,
由根与系数的关系可知x0-1=<0,故b<0,
故f(-1)+f(1)=-2b>0,C正确;
因为f′(x)=3ax2-2bx+c的图象是开口向上的抛物线,对称轴方程为x==<0,
所以f′(x)在区间上单调递减,在区间上单调递增,D错误.]
9.ACD [对任意两个不相等的实数x1,x2,都有x1f+x2f>x1f+x2f恒成立,
所以不等式等价于(x1-x2)[f(x1)-f(x2)]>0恒成立,
即函数f(x)是增函数,
对于A,函数f(x)=3x-sin x,可得f′(x)=3-cos x>0,
函数f(x)是增函数,符合题意;
对于B,函数f(x)=当x>0时,函数y=ln x单调递增,
当x<0时,函数y=ln(-x)单调递减,不符合题意;
对于C,由函数f(x)=x3+3x,可得f′(x)=3x2+3>0,可得f(x)是增函数,符合题意;
对于D,函数f(x)=ex+x,
可得f′(x)=ex+1>0,
可得f(x)是增函数,符合题意.]
10.1
解析 因为f(x)=2x,所以f′(x)=2xln 2,
又f′=ln 4,所以=ln 4=2ln 2,解得x0=1.
11.1
解析 从导函数的图象上可得导数的零点有4个,
其中满足零点左侧附近导数小于零且右侧附近导数大于零的零点有1个.
12.
解析 f(x)=(-x2+ax)ex,
则f′(x)=ex,
函数f(x)=(-x2+ax)ex在区间(-1,1)上存在减区间,只需-x2+ax-2x+a<0在区间上有解.
记g(x)=-x2+x+a,其对称轴为直线x=,开口向下,g=-1-+a=1>0,只需g<0,
所以-1+a-2+a<0,解得a<.
13.解 (1)由f(x)=x3-x得f′(x)=3x2-1,
则f′(-1)=3-1=2,
所以曲线在点(-1,0)处的切线方程为y=2(x+1),即y=2x+2.
(2)设切点为(x0,x-x0),
则f′(x0)=3x-1,
则切线方程为y=(3x-1)(x-x0)+x-x0,
因为切线过点(-1,0),代入切线方程得,
0=(3x-1)(-1-x0)+x-x0,化简得2x+3x-1=0,
则(x0+1)2(2x0-1)=0 x0=-1或x0=,
所以曲线过点(-1,0)的切线方程为
y=2x+2或y=-x-.
(3)直线11x-y+1=0的斜率为11,
设切点为(x1,x-x1),则f′(x1)=3x-1,
则切线方程为y=(3x-1)(x-x1)+x-x1,
则由切线与直线11x-y+1=0平行得3x-1=11 x=4,
即x1=2或x1=-2,
所以切线方程为y=11x-16或y=11x+16.
14.解 函数f(x)=kx-ln x的定义域为(0,+∞),
f′(x)=k-=.
当k≤0时,kx-1<0,∴f′(x)<0,
则f(x)是减函数.
当k>0时,由f′(x)<0,即<0,
解得0
∴当k>0时,f(x)在区间上单调递减,
在区间上单调递增.
综上所述,当k≤0时,f(x)的减区间为(0,+∞),无增区间;
当k>0时,f(x)的减区间为,增区间为.
15.解 (1)f(x)的定义域为R,f′(x)=,
当x∈(-∞,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,所以f(x)在区间(-∞,1)上单调递减,在区间(1,+∞)上单调递增.
所以f(x)有极小值f(1)=,无极大值.
(2)由(1)知,f(x)在区间(1,+∞)上单调递增.
则g(x)在区间(1,+∞)上单调递增,即g′(x)=1+ln x-ax-1=ln x-ax≥0在(1,+∞)上恒成立,即a≤在(1,+∞)上恒成立,
令p(x)=,x∈(1,+∞),则p′(x)=,
所以当x∈(1,e)时,p′(x)>0;当x∈(e,+∞)时,p′(x)<0,
所以p(x)在区间(1,e)上单调递增,在区间(e,+∞)上单调递减,又x∈(1,+∞)时,p(x)>0,所以p(x)∈,所以a≤0.
