福建省泉州市2023-2024学年高一下学期期末数学试卷(PDF版,含答案)
文档属性
| 名称 | 福建省泉州市2023-2024学年高一下学期期末数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 841.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 17:41:15 | ||
图片预览



文档简介
福建省泉州市 2023-2024 学年高一下学期期末数学试卷
一、单选题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数 满足 = 2 , 是虚数单位,则| | =( )
A. √ 2 B. √ 3 C. 2 D. √ 5
2.从甲、乙、丙三所学校中随机抽取210名学生,接受省级高中体育与健康教育质量监测.已知甲、乙、丙三
所学校的学生人数分别为400,700,1000,若按各校人数分层抽样,则从甲学校中应抽取的学生人数为( )
A. 40 B. 50 C. 60 D. 70
3.单位向量 , 满足| + | = √ 3| |,则 和 的夹角为( )
A. 30° B. 60° C. 120° D. 150°
4.在△ 中, = 3 ,则 =( )
2 1 1 2 3 1 1 3
A. + B. + C. + D. +
3 3 3 3 4 4 4 4
5.如图是一个鲜花包装盒,形状近似于高为12 的正四棱台,其两个底面边长分别为8 和10 .
若忽略材料厚度,则该包装盒的容积为( )
A. 960 3
B. 976 3
C. 2880 3
D. 2928 3
6.已知数据 1, 2, 3, , 的均值为3,方差为1,则数据2 1 + 3,2 2 + 3,2 3 + 3, ,2 + 3的
均值和方差分别为( )
A. 9,5 B. 6,5 C. 9,4 D. 6,4
7.已知直线 , ,平面 , ,则 // 的充分条件可以是( )
A. , // B. // , ,
C. // , // , ∩ = D. ⊥ , ⊥ , //
8.《周易 系辞》曰:易有太极,是生两仪,两仪生四象,四象生八卦.如
图1是八卦模型图,图2是根据八卦图抽象而得的正八边形 与
12
其内部的圆 ,其中 = 2,圆 的直径 为 , 为正八边形的中心,
5
为正八边形边上的动点,则 的最小值为( )
第 1 页,共 9 页
26 39 41 64
A. + 2√ 2 B. + 2√ 2 C. + 2√ 2 D. + 2√ 2
25 25 25 25
二、多选题:本题共 3 小题,共 18 分。在每小题给出的选项中,有多项符合题目要求。
9.已知 1, 2为复数,则下列命题正础的是( )
A. 若 1 = 2,则 1 2 ∈ B. | 1 + 2| ≥ | 1| + | 2|
C. 若 21 +
2
2 = 0,则 1 = 2 = 0 D. | 1 2| = | 1|| 2|
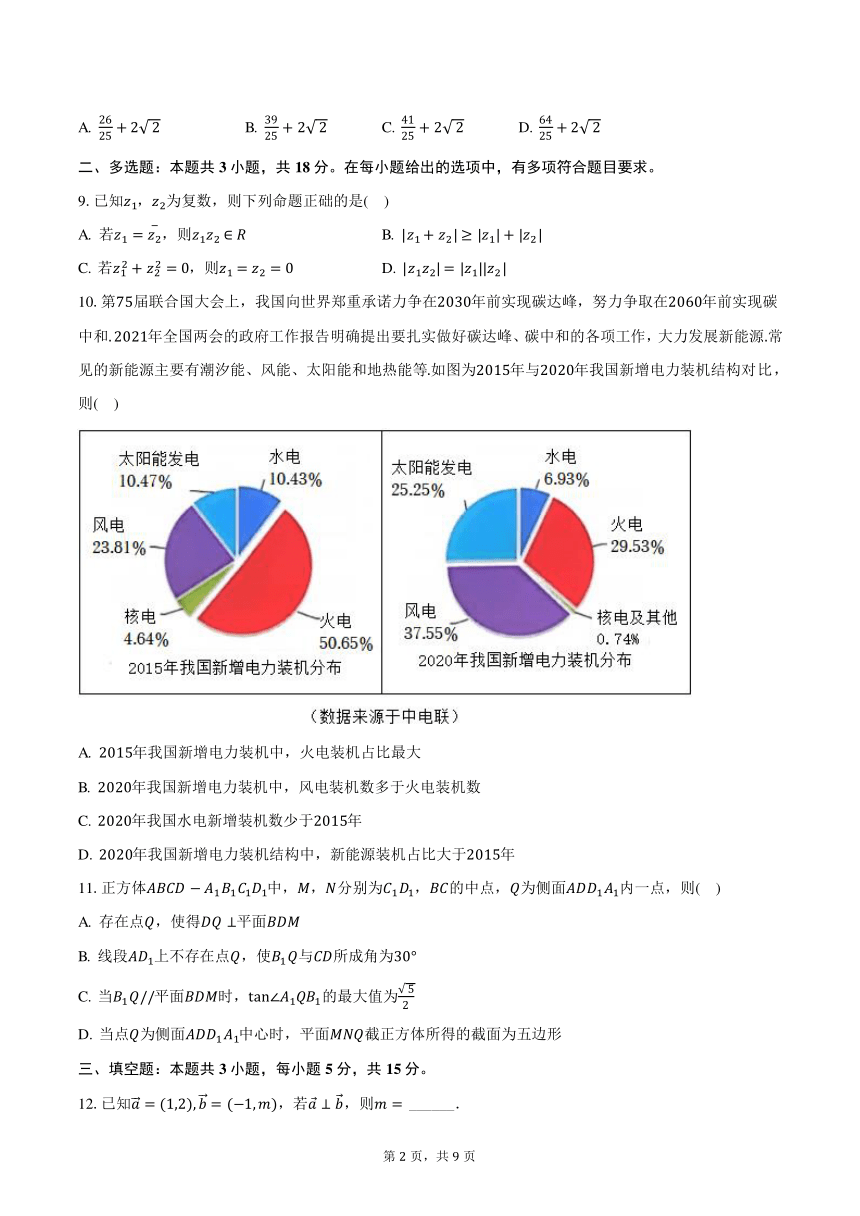
10.第75届联合国大会上,我国向世界郑重承诺力争在2030年前实现碳达峰,努力争取在2060年前实现碳
中和. 2021年全国两会的政府工作报告明确提出要扎实做好碳达峰、碳中和的各项工作,大力发展新能源.常
见的新能源主要有潮汐能、风能、太阳能和地热能等.如图为2015年与2020年我国新增电力装机结构对比,
则( )
A. 2015年我国新增电力装机中,火电装机占比最大
B. 2020年我国新增电力装机中,风电装机数多于火电装机数
C. 2020年我国水电新增装机数少于2015年
D. 2020年我国新增电力装机结构中,新能源装机占比大于2015年
11.正方体 1 1 1 1中, , 分别为 1 1, 的中点, 为侧面 1 1内一点,则( )
A. 存在点 ,使得 ⊥平面
B. 线段 1上不存在点 ,使 1 与 所成角为30°
√ 5
C. 当 1 //平面 时,tan∠ 1 1的最大值为 2
D. 当点 为侧面 1 1中心时,平面 截正方体所得的截面为五边形
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
12.已知 = (1,2), = ( 1, ),若 ⊥ ,则 = ______.
第 2 页,共 9 页
13.已知△ 中, = 2√ 2, = 1,向量 在向量 上的投影向量为 2 ,则∠ = ______.
14.已知圆锥的顶点 和底面圆周都在球 的球面上,且母线长为2, , 为其底面圆周上的两点,若△
面积的最大值为√ 3,则球 的表面积为______.
四、解答题:本题共 5 小题,共 77 分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
如图,△ 的内角 , , 所对的边分别为 , , , 为△ 外一点, = 1, = √ 3, ∠ = 60°.
(1)求 ;
(2)若 = 45°, = ,求△ 的面积.
16.(本小题15分)
盒子中有4个大小质地完全相同的小球,分别标有数字1,2,3,4,从盒子中有放回地随机两次摸出小球,
每次摸出一个小球.
(1)求两次摸到的小球数字之和为偶数的概率;
(2)设事件 =“两次摸到的小球数字之和是质数”,事件 1 =“第1次摸到的小球数字为奇数”,事件
2 =“第2次摸到的小球数字为奇数”,求 ( 1 2 ∪ 1 2 ∪ 1 2).
17.(本小题15分)
如图,在三棱柱 1 1 1中,平面 ⊥平面 1 1, = = 1 = √ 3, 1 = √ 6,∠ = 120°.
(1)求三棱柱 1 1 1的体积;
(2)求证: 1 1 ⊥ 1B.
第 3 页,共 9 页
18.(本小题17分)
“泉州:宋元中国的世界海洋商贸中心”于2021年7月25日成功列入《世界遗产名录》,成为中国第56处
世界遗产,泉州在持续做好世界遗产保护的同时,积极推动文化和旅游的深度融合,在2024年“五一”假
期期间,为了解全国各地游客对泉州某景点的满意度,景区在该景点向游客做随机问卷调查,收集了1000份
问卷,并统计每份问卷的得分(百分制),绘制了如下频率分布直方图:
(1)求 ;
(2)估计该满意度得分的第一四分位数和总体平均数;
(3)已知填写问卷的游客中,儿童、中青年人、老年人的比例为1:7:2,其中儿童游客满意度得分的平均
数为86,方差为45.15;老年人游客满意度得分的平均数为96,方差为10.55.请结合频率分布直方图,估计
中青年游客对该景点满意度得分的平均数和方差.
19.(本小题17分)
一般地,任何一个复数 = + ( , ∈ )都可以表示成 ( + )( > 0)的形式, ( + )叫
做复数 = + 的三角表示式,简称三角形式.
√ 3 1
(1)写出复数 = + 的三角形式;
2 2
(2)阅读材料:
数学家布鲁克 泰勒提出利用多项式函数曲线来逼近任意一个原函数曲线的泰勒公式,在近似计算、函数拟
合和计算机科学上有着举足轻重的作用.如下列常见函数的 阶泰勒展开式为:
2 3
= 1 + + + + + + ,
2! 3! !
3 5 2 +1
= + + ( 1) + ,
3! 5! (2 +1)!
2 4 2
= 1 + + ( 1) + ,其中 ! = 1 × 2 × 3 × × ,读作 的阶乘.
2! 4! (2 )!
第 4 页,共 9 页
数学家莱昂哈德 欧拉在泰勒公式的灵感下,把自然对数的底数 ,虚数单位 ,三角函数联系在一起创造了
欧拉公式: = + ,该公式将指数函数的定义域扩大到复数集,在复变函数论里面占有非常重
要的地位,被誉为数学中的天桥.
数学家棣莫弗发现 = 11 1 = 1( 1 + 1), 2 = 2
2 = 2( 2 + 2),则 1 2 =
1 2[cos( 1 + 2) + ( 1 + 2)].特别地,如果 1 = 2 = = = ( + ),那么[ ( +
)] = ( + ),这个结论叫做棣莫弗定理,该定理为概率论的发展做出重要的贡献.
(ⅰ)利用泰勒展开式求sin( 1)的近似值(精确到0.001);
2
√ 3+
(ⅱ)设 = { ∈ | = [( )13 1] , ∈ , 1 ≤ ≤ 2024},求集合 的元素个数.
2
第 5 页,共 9 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
1
12.【答案】
2
3
13.【答案】
4
16
14.【答案】
3
15.【答案】解:(1)在△ 中,由余弦定理得:
2 = 2 + 2 2 cos∠ ,
1
将 = 1, = √ 3, ∠ = 60°代入得3 = 1 + 2 2 × ,
2
即 2 2 = 0,
解得 = 2或 = 1(舍去),
所以 = 2.
(2)在△ 中,由正弦定理得:
= 可化为 = ,
所以 = = sin( + ) = + ,
整理得 = 0,又因为 > 0,
所以 = 0,
所以 = 90°,△ 为等腰直角三角形,
1
则△ 的面积为 × 2 × 2 = 2.
2
第 6 页,共 9 页
16.【答案】解:(1)从盒中有放回依次随机摸出两个小球的样本空间是:
= {(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),
(4,3),(4,4),
所以 ( ) = 16,共有16个样本点.
记事件 =“两次摸到的小球数字之和为偶数”,
则 = {(1,1),(1,3),(2,2),(2,4),(3,1),(3,3),(4,2),(4,4)},
所以 ( ) = 8,共有8个样本点.
因为样本空间的每个样本点具有等可能性,
( ) 8 1
所以 ( ) = = = ,
( ) 16 2
1
即两次摸出的小球数字之和为偶数的概率为 .
2
9
(2)因为 = {(1,1),(1,2),(1,4),(2,1),(2,3),(3,2),(3,4),(4,1),(4,3)},则 ( ) = ,
16
1 = {(1,1),(1,2),(1,3),(1,4),(3,1),(3,2),(3,3),(3,4)},
2 = {(1,1),(1,3),(2,1),(2,3),(3,1),(3,3),(4,1),(4,3)},
1
所以 1 2 = {(1,1)},则 ( 1 2) = , 16
因为事件 1 2、 1 2、 1 2,
不会同时发生,所以两两互斥,所以 ( 1 2 ∪ 1 2 ∪ 1 2) = ( 1 2) + ( 1 2) + ( 1 2),
又因为 ( 1 2) + ( 1 2) + ( 1 2) + ( 1 2) = ( ),
9 1 1
所以 ( 1 2) + ( 1 2) + ( 1 2) = ( ) ( 1 2) = = . 16 16 2
1
即可得 ( 1 2 ∪ 1 2 ∪ 1 2) = . 2
17.【答案】解:(1)过点 1作 1 ⊥ ,垂足为 , 1
平面 1 1,
因为平面 ⊥平面 1 1,平面 ∩平面 1 1 =
,
所以 1 ⊥平面 ,
1
在△ 中, 2 = 2 + 2 2 cos∠ = 3 + 3 2 × 3 × ( ) = 9,
2
所以 = 3, 21 + 1
2 = 2,△ 1 为直角三角形,
第 7 页,共 9 页
1 1
在 △ 1 中,由 △ = 1 1 = 1 , 1 2 2
解得 1 =
1 1 = √ 2,
1 3√ 6
所以 三棱柱 = △ 1 = × √ 3 × √ 3 × 120° × √ 2 = ; 1 1 1 2 4
(2)证明:在△ 1 中,
2 = 1
2 21 = 4,即 = 2,
√ 3
在△ 中, 2 = 2 + 2 2 cos∠ = 4 + 3 2 × 2 × √ 3 × = 1,
2
因为 1 ⊥平面 , 平面 ,所以 1 ⊥ ,
在 △ 1 中,
2
1 =
2 2
1 + = 3,
则 1
2 + 2 = 1
2,
所以 ⊥ 1 ,
因为 // 1 1,
所以 1 1 ⊥ 1B.
18【. 答案】解:(1)由频率分布直方图得:0.002 × 5 + 0.01 × 5 + 0.02 × 5 + 0.02 × 5 + × 5 + 0.058 × 5 = 1,
解得 = 0.09;
(2)0.01 + 0.05 + 0.1 < 0.25 < 0.01 + 0.05 + 0.1 + 0.1,
由频率分布直方图,第一四分位数落在区间[85,90)之间,
0.25 0.16
由85 + 5 × = 89.5,
0.1
可以估计该满意度得分的第一四分位数为89.5,
1000份问卷的平均分可估计为:
= 72.5 × 0.01 + 77.5 × 0.05 + 82.5 × 0.1 + 87.5 × 0.1 + 92.5 × 0.45 + 97.5 × 0.29 = 91.5,
用样本估计总体,可以估计游客对该景点满意度的总体平均数为91.5;
(3)由频率分布直方图,1000份问卷的方差可估计为:
2 = (72.5 91.5)2 × 0.01 + (77.5 91.5)2 × 0.05 + (82.5 91.5)2 × 0.1 + (87.5 91.5)2 × 0.1 + (92.5
91.5)2 × 0.45 + (97.5 91.5)2 × 0.29 = 34,
用样本估计总体,则所有游客满意度平均分为 = 91.5,方差为 2 = 34,
儿童游客满意度平均分为 1 = 86,方差为
2
1 = 45.15,
老年人游客满意度平均分为 3 = 96,方差为
2
3 = 10.55,
估计中青年游客对该景点满意度的平均分为 2,方差
2
2,
则 = 1 × 0.1 + 2 × 0.7 + 3 × 0.2 = 86 × 0.1 + 2 × 0.7 + 96 × 0.2 = 91.5,
第 8 页,共 9 页
解得 2 = 91,
2 = 0.1 × [45.15 + (86 91.5)2] + 0.7 × [ 22 + (91 91.5)
2] + 0.2 + [10.55 + (96 91.5)2] = 34,
解得 22 = 28.75,
所以估计中青年游客对该景点满意度的平均分为91,方差28.75.
√ 3 1 5 5
19.【答案】解:(1) + = cos + sin .
2 2 6 6
(2)(ⅰ)sin( 1)的近似值为sin( 1) = 1
2 2
12 14 16 18 110 1 1 1 1 1
= 1 + + + = 1 + + +
2! 4! 6! 8! 10! 2 24 720 40320 3628800
29
≈ 1 0.5 + = 0.5 + 0.0402 ≈ 0.540;
720
√ 3+ 5 5
(ⅰ)[( )13 1] = [(cos + )13 1]
2 6 6
65 65
= [cos + 1]
6 6
5 5
= [cos 1 + ]
6 6
5 5 5
= [1 2 2 1 + 2 cos ]
12 12 12
5 5 5
= [ 2 2 + 2 cos ]
12 12 12
5 5 5
= (2 ) [ sin + ]
12 12 12
5 11 11
= (2 ) [cos + ]
12 12 12
5 11 11
= (2 ) [cos + ]
12 12 12
11
依题可知 = 0,
12
11
所以 = , ∈ , ∈ ,
12
即 = 12 , ∈ ,又因为1 ≤ ≤ 2024,
所以1 ≤ 12 ≤ 2024, ∈ ,即1 ≤ ≤ 168, ∈ ,
√ 3+
10故[( )13 1] 的值中有168个实数,
2
即集合 的元素个数为168.
第 9 页,共 9 页
一、单选题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数 满足 = 2 , 是虚数单位,则| | =( )
A. √ 2 B. √ 3 C. 2 D. √ 5
2.从甲、乙、丙三所学校中随机抽取210名学生,接受省级高中体育与健康教育质量监测.已知甲、乙、丙三
所学校的学生人数分别为400,700,1000,若按各校人数分层抽样,则从甲学校中应抽取的学生人数为( )
A. 40 B. 50 C. 60 D. 70
3.单位向量 , 满足| + | = √ 3| |,则 和 的夹角为( )
A. 30° B. 60° C. 120° D. 150°
4.在△ 中, = 3 ,则 =( )
2 1 1 2 3 1 1 3
A. + B. + C. + D. +
3 3 3 3 4 4 4 4
5.如图是一个鲜花包装盒,形状近似于高为12 的正四棱台,其两个底面边长分别为8 和10 .
若忽略材料厚度,则该包装盒的容积为( )
A. 960 3
B. 976 3
C. 2880 3
D. 2928 3
6.已知数据 1, 2, 3, , 的均值为3,方差为1,则数据2 1 + 3,2 2 + 3,2 3 + 3, ,2 + 3的
均值和方差分别为( )
A. 9,5 B. 6,5 C. 9,4 D. 6,4
7.已知直线 , ,平面 , ,则 // 的充分条件可以是( )
A. , // B. // , ,
C. // , // , ∩ = D. ⊥ , ⊥ , //
8.《周易 系辞》曰:易有太极,是生两仪,两仪生四象,四象生八卦.如
图1是八卦模型图,图2是根据八卦图抽象而得的正八边形 与
12
其内部的圆 ,其中 = 2,圆 的直径 为 , 为正八边形的中心,
5
为正八边形边上的动点,则 的最小值为( )
第 1 页,共 9 页
26 39 41 64
A. + 2√ 2 B. + 2√ 2 C. + 2√ 2 D. + 2√ 2
25 25 25 25
二、多选题:本题共 3 小题,共 18 分。在每小题给出的选项中,有多项符合题目要求。
9.已知 1, 2为复数,则下列命题正础的是( )
A. 若 1 = 2,则 1 2 ∈ B. | 1 + 2| ≥ | 1| + | 2|
C. 若 21 +
2
2 = 0,则 1 = 2 = 0 D. | 1 2| = | 1|| 2|
10.第75届联合国大会上,我国向世界郑重承诺力争在2030年前实现碳达峰,努力争取在2060年前实现碳
中和. 2021年全国两会的政府工作报告明确提出要扎实做好碳达峰、碳中和的各项工作,大力发展新能源.常
见的新能源主要有潮汐能、风能、太阳能和地热能等.如图为2015年与2020年我国新增电力装机结构对比,
则( )
A. 2015年我国新增电力装机中,火电装机占比最大
B. 2020年我国新增电力装机中,风电装机数多于火电装机数
C. 2020年我国水电新增装机数少于2015年
D. 2020年我国新增电力装机结构中,新能源装机占比大于2015年
11.正方体 1 1 1 1中, , 分别为 1 1, 的中点, 为侧面 1 1内一点,则( )
A. 存在点 ,使得 ⊥平面
B. 线段 1上不存在点 ,使 1 与 所成角为30°
√ 5
C. 当 1 //平面 时,tan∠ 1 1的最大值为 2
D. 当点 为侧面 1 1中心时,平面 截正方体所得的截面为五边形
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
12.已知 = (1,2), = ( 1, ),若 ⊥ ,则 = ______.
第 2 页,共 9 页
13.已知△ 中, = 2√ 2, = 1,向量 在向量 上的投影向量为 2 ,则∠ = ______.
14.已知圆锥的顶点 和底面圆周都在球 的球面上,且母线长为2, , 为其底面圆周上的两点,若△
面积的最大值为√ 3,则球 的表面积为______.
四、解答题:本题共 5 小题,共 77 分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
如图,△ 的内角 , , 所对的边分别为 , , , 为△ 外一点, = 1, = √ 3, ∠ = 60°.
(1)求 ;
(2)若 = 45°, = ,求△ 的面积.
16.(本小题15分)
盒子中有4个大小质地完全相同的小球,分别标有数字1,2,3,4,从盒子中有放回地随机两次摸出小球,
每次摸出一个小球.
(1)求两次摸到的小球数字之和为偶数的概率;
(2)设事件 =“两次摸到的小球数字之和是质数”,事件 1 =“第1次摸到的小球数字为奇数”,事件
2 =“第2次摸到的小球数字为奇数”,求 ( 1 2 ∪ 1 2 ∪ 1 2).
17.(本小题15分)
如图,在三棱柱 1 1 1中,平面 ⊥平面 1 1, = = 1 = √ 3, 1 = √ 6,∠ = 120°.
(1)求三棱柱 1 1 1的体积;
(2)求证: 1 1 ⊥ 1B.
第 3 页,共 9 页
18.(本小题17分)
“泉州:宋元中国的世界海洋商贸中心”于2021年7月25日成功列入《世界遗产名录》,成为中国第56处
世界遗产,泉州在持续做好世界遗产保护的同时,积极推动文化和旅游的深度融合,在2024年“五一”假
期期间,为了解全国各地游客对泉州某景点的满意度,景区在该景点向游客做随机问卷调查,收集了1000份
问卷,并统计每份问卷的得分(百分制),绘制了如下频率分布直方图:
(1)求 ;
(2)估计该满意度得分的第一四分位数和总体平均数;
(3)已知填写问卷的游客中,儿童、中青年人、老年人的比例为1:7:2,其中儿童游客满意度得分的平均
数为86,方差为45.15;老年人游客满意度得分的平均数为96,方差为10.55.请结合频率分布直方图,估计
中青年游客对该景点满意度得分的平均数和方差.
19.(本小题17分)
一般地,任何一个复数 = + ( , ∈ )都可以表示成 ( + )( > 0)的形式, ( + )叫
做复数 = + 的三角表示式,简称三角形式.
√ 3 1
(1)写出复数 = + 的三角形式;
2 2
(2)阅读材料:
数学家布鲁克 泰勒提出利用多项式函数曲线来逼近任意一个原函数曲线的泰勒公式,在近似计算、函数拟
合和计算机科学上有着举足轻重的作用.如下列常见函数的 阶泰勒展开式为:
2 3
= 1 + + + + + + ,
2! 3! !
3 5 2 +1
= + + ( 1) + ,
3! 5! (2 +1)!
2 4 2
= 1 + + ( 1) + ,其中 ! = 1 × 2 × 3 × × ,读作 的阶乘.
2! 4! (2 )!
第 4 页,共 9 页
数学家莱昂哈德 欧拉在泰勒公式的灵感下,把自然对数的底数 ,虚数单位 ,三角函数联系在一起创造了
欧拉公式: = + ,该公式将指数函数的定义域扩大到复数集,在复变函数论里面占有非常重
要的地位,被誉为数学中的天桥.
数学家棣莫弗发现 = 11 1 = 1( 1 + 1), 2 = 2
2 = 2( 2 + 2),则 1 2 =
1 2[cos( 1 + 2) + ( 1 + 2)].特别地,如果 1 = 2 = = = ( + ),那么[ ( +
)] = ( + ),这个结论叫做棣莫弗定理,该定理为概率论的发展做出重要的贡献.
(ⅰ)利用泰勒展开式求sin( 1)的近似值(精确到0.001);
2
√ 3+
(ⅱ)设 = { ∈ | = [( )13 1] , ∈ , 1 ≤ ≤ 2024},求集合 的元素个数.
2
第 5 页,共 9 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
1
12.【答案】
2
3
13.【答案】
4
16
14.【答案】
3
15.【答案】解:(1)在△ 中,由余弦定理得:
2 = 2 + 2 2 cos∠ ,
1
将 = 1, = √ 3, ∠ = 60°代入得3 = 1 + 2 2 × ,
2
即 2 2 = 0,
解得 = 2或 = 1(舍去),
所以 = 2.
(2)在△ 中,由正弦定理得:
= 可化为 = ,
所以 = = sin( + ) = + ,
整理得 = 0,又因为 > 0,
所以 = 0,
所以 = 90°,△ 为等腰直角三角形,
1
则△ 的面积为 × 2 × 2 = 2.
2
第 6 页,共 9 页
16.【答案】解:(1)从盒中有放回依次随机摸出两个小球的样本空间是:
= {(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),
(4,3),(4,4),
所以 ( ) = 16,共有16个样本点.
记事件 =“两次摸到的小球数字之和为偶数”,
则 = {(1,1),(1,3),(2,2),(2,4),(3,1),(3,3),(4,2),(4,4)},
所以 ( ) = 8,共有8个样本点.
因为样本空间的每个样本点具有等可能性,
( ) 8 1
所以 ( ) = = = ,
( ) 16 2
1
即两次摸出的小球数字之和为偶数的概率为 .
2
9
(2)因为 = {(1,1),(1,2),(1,4),(2,1),(2,3),(3,2),(3,4),(4,1),(4,3)},则 ( ) = ,
16
1 = {(1,1),(1,2),(1,3),(1,4),(3,1),(3,2),(3,3),(3,4)},
2 = {(1,1),(1,3),(2,1),(2,3),(3,1),(3,3),(4,1),(4,3)},
1
所以 1 2 = {(1,1)},则 ( 1 2) = , 16
因为事件 1 2、 1 2、 1 2,
不会同时发生,所以两两互斥,所以 ( 1 2 ∪ 1 2 ∪ 1 2) = ( 1 2) + ( 1 2) + ( 1 2),
又因为 ( 1 2) + ( 1 2) + ( 1 2) + ( 1 2) = ( ),
9 1 1
所以 ( 1 2) + ( 1 2) + ( 1 2) = ( ) ( 1 2) = = . 16 16 2
1
即可得 ( 1 2 ∪ 1 2 ∪ 1 2) = . 2
17.【答案】解:(1)过点 1作 1 ⊥ ,垂足为 , 1
平面 1 1,
因为平面 ⊥平面 1 1,平面 ∩平面 1 1 =
,
所以 1 ⊥平面 ,
1
在△ 中, 2 = 2 + 2 2 cos∠ = 3 + 3 2 × 3 × ( ) = 9,
2
所以 = 3, 21 + 1
2 = 2,△ 1 为直角三角形,
第 7 页,共 9 页
1 1
在 △ 1 中,由 △ = 1 1 = 1 , 1 2 2
解得 1 =
1 1 = √ 2,
1 3√ 6
所以 三棱柱 = △ 1 = × √ 3 × √ 3 × 120° × √ 2 = ; 1 1 1 2 4
(2)证明:在△ 1 中,
2 = 1
2 21 = 4,即 = 2,
√ 3
在△ 中, 2 = 2 + 2 2 cos∠ = 4 + 3 2 × 2 × √ 3 × = 1,
2
因为 1 ⊥平面 , 平面 ,所以 1 ⊥ ,
在 △ 1 中,
2
1 =
2 2
1 + = 3,
则 1
2 + 2 = 1
2,
所以 ⊥ 1 ,
因为 // 1 1,
所以 1 1 ⊥ 1B.
18【. 答案】解:(1)由频率分布直方图得:0.002 × 5 + 0.01 × 5 + 0.02 × 5 + 0.02 × 5 + × 5 + 0.058 × 5 = 1,
解得 = 0.09;
(2)0.01 + 0.05 + 0.1 < 0.25 < 0.01 + 0.05 + 0.1 + 0.1,
由频率分布直方图,第一四分位数落在区间[85,90)之间,
0.25 0.16
由85 + 5 × = 89.5,
0.1
可以估计该满意度得分的第一四分位数为89.5,
1000份问卷的平均分可估计为:
= 72.5 × 0.01 + 77.5 × 0.05 + 82.5 × 0.1 + 87.5 × 0.1 + 92.5 × 0.45 + 97.5 × 0.29 = 91.5,
用样本估计总体,可以估计游客对该景点满意度的总体平均数为91.5;
(3)由频率分布直方图,1000份问卷的方差可估计为:
2 = (72.5 91.5)2 × 0.01 + (77.5 91.5)2 × 0.05 + (82.5 91.5)2 × 0.1 + (87.5 91.5)2 × 0.1 + (92.5
91.5)2 × 0.45 + (97.5 91.5)2 × 0.29 = 34,
用样本估计总体,则所有游客满意度平均分为 = 91.5,方差为 2 = 34,
儿童游客满意度平均分为 1 = 86,方差为
2
1 = 45.15,
老年人游客满意度平均分为 3 = 96,方差为
2
3 = 10.55,
估计中青年游客对该景点满意度的平均分为 2,方差
2
2,
则 = 1 × 0.1 + 2 × 0.7 + 3 × 0.2 = 86 × 0.1 + 2 × 0.7 + 96 × 0.2 = 91.5,
第 8 页,共 9 页
解得 2 = 91,
2 = 0.1 × [45.15 + (86 91.5)2] + 0.7 × [ 22 + (91 91.5)
2] + 0.2 + [10.55 + (96 91.5)2] = 34,
解得 22 = 28.75,
所以估计中青年游客对该景点满意度的平均分为91,方差28.75.
√ 3 1 5 5
19.【答案】解:(1) + = cos + sin .
2 2 6 6
(2)(ⅰ)sin( 1)的近似值为sin( 1) = 1
2 2
12 14 16 18 110 1 1 1 1 1
= 1 + + + = 1 + + +
2! 4! 6! 8! 10! 2 24 720 40320 3628800
29
≈ 1 0.5 + = 0.5 + 0.0402 ≈ 0.540;
720
√ 3+ 5 5
(ⅰ)[( )13 1] = [(cos + )13 1]
2 6 6
65 65
= [cos + 1]
6 6
5 5
= [cos 1 + ]
6 6
5 5 5
= [1 2 2 1 + 2 cos ]
12 12 12
5 5 5
= [ 2 2 + 2 cos ]
12 12 12
5 5 5
= (2 ) [ sin + ]
12 12 12
5 11 11
= (2 ) [cos + ]
12 12 12
5 11 11
= (2 ) [cos + ]
12 12 12
11
依题可知 = 0,
12
11
所以 = , ∈ , ∈ ,
12
即 = 12 , ∈ ,又因为1 ≤ ≤ 2024,
所以1 ≤ 12 ≤ 2024, ∈ ,即1 ≤ ≤ 168, ∈ ,
√ 3+
10故[( )13 1] 的值中有168个实数,
2
即集合 的元素个数为168.
第 9 页,共 9 页
同课章节目录
