期末模拟预测试卷人教版数学六年级上册(含答案)
文档属性
| 名称 | 期末模拟预测试卷人教版数学六年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 09:29:04 | ||
图片预览




文档简介
期末模拟预测试卷 人教版数学六年级上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个数的是36的,这个数是( )。
A.60 B.50 C.30
2.学校里的升旗台在荷花池的南偏西25°方向200米处,下面图( )符合这句话的描述。
A. B. C.
3.做一个零件,甲要4分钟完成,乙要5分钟完成,甲的工效是乙的( )。
A.80% B.120% C.125%
4.如下图,从甲地到乙地,A、B两条路线的长度相比,( )。
A.A长一些 B.B长一些 C.一样长
5.甲、乙、丙三个数的和是300,甲数是120,乙数与丙数的比是2∶3,丙数是( )。
A.72 B.108 C.180
6.甲乙两根同样长的铁丝,甲用去,乙用去米,剩下的长度比较,( )。
A.甲长 B.乙长 C.无法确定哪根长
二、填空题
7.。
8.计算综合算式:-÷1.2时,应该先算( )法,再算( )法,最后算( )法。
9.如图:丽丽要从学校沿( 偏 )( )°方向走( )米去足球场训练。
10.白兔只数的相当于黑兔的只数,这句话是把( )看作单位“1”;黑兔只数比白兔只数少。
11.给4∶5的前项加上20,要使比值不变,比的后项应加上( )。
12.钟面上分针从12走到3,分针扫过的部分是个( )形,它的圆心角是( )度。
13.每年的梅雨季节都是梁子湖的防汛期,为了观察这一期间的温度变化情况,应选用( )统计图;为了反映出这期间各类天气占总天数的百分比,应选用( )统计图。
14.修一条公路,王师傅单独工作需要20天完成,李师傅每天修整条公路的,如两人合作,( )天后完成这条公路的50%。
15.有一只羊被拴在一间底面边长为3m正方形小房子的墙角B点(如下图),拴羊的绳子长8m,这只羊从A点出发,将绳子拉紧顺时针跑,最多可跑( )m。
16.一个长方体的棱长和是48cm,长、宽、高的比是5∶3∶4,这个长方体的表面积为( ),体积为( )。
17.要组装一批手表,如果徒弟单独完成需要18天,而师父与徒弟合作需要6天可以完成,那么师父单独完成需要( )天。
18.根据下面的规律,算一算。
1+3+5+7+9+7+5+3+1=( )。
三、计算题
19.直接写得数。
×5= ×= ÷= ÷4= 0.3×80%=
4.2×= +=
20.看清题目,细心计算。(下面各题怎样算简便就怎样算。)
21.解方程。
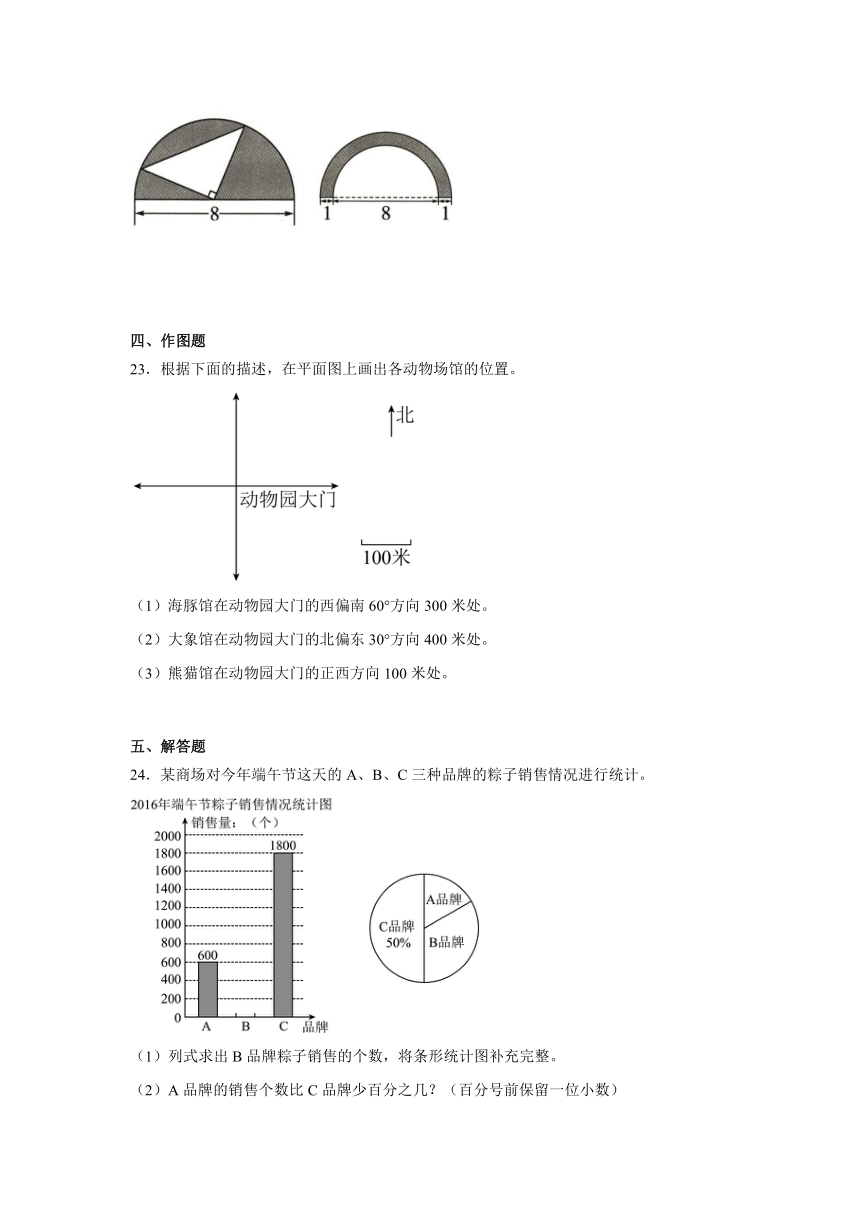
22.我会计算下面图形阴影部分的面积。(单位:cm)
四、作图题
23.根据下面的描述,在平面图上画出各动物场馆的位置。
(1)海豚馆在动物园大门的西偏南60°方向300米处。
(2)大象馆在动物园大门的北偏东30°方向400米处。
(3)熊猫馆在动物园大门的正西方向100米处。
五、解答题
24.某商场对今年端午节这天的A、B、C三种品牌的粽子销售情况进行统计。
(1)列式求出B品牌粽子销售的个数,将条形统计图补充完整。
(2)A品牌的销售个数比C品牌少百分之几?(百分号前保留一位小数)
25.一个垃圾处理厂平均每天收到60吨生活垃圾,其中可回收利用的垃圾占,这个垃圾处理厂一周收到的垃圾中有多少吨可回收利用?
26.在运动会的“8字跳绳”比赛中,六一班跳绳数量是六二班的,六三班与六二班的比是9∶8,六一班共跳280个,你知道六三班跳了多少个吗?
27.儿童广场里有一块面积为700平方米的圆形草坪,要在草坪上安装一个自动旋转喷灌装置进行喷灌。现在有射程是15米和10米的两种装置,你认为应该选哪种装置比较合适?你打算把它安装在什么位置?请写出推理过程。
28.服装厂接到一批订单,第一车间单独做需要10天完成,第二车间单独做3天完成了,如果两个车间同时做这批订单,多少天可以完成这批订单?
29.实验小学组织五、六年级的同学种一批树苗,把这批树苗按5∶8分配给五、六年级。植树结束后,李老师发现:六年级同学完成分配任务后,又帮助五年级同学种植了一些正好一共种植了2000棵,超额完成分配任务的25%,而五年级同学只完成了分配任务的60%。五年级同学实际种植了多少棵?
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据分数乘法的意义,求一个数的几分之几是多少,用乘法,用36乘求出结果为30。再根据分数除法的意义,已知一个数的几分之几是多少,求这个数,用除法,用30除以,即可求出这个数。
【解答】36×÷
=30÷
=30×
=50
即这个数是50。
故答案为:B
【点评】此题的解题关键是理解分数乘法和分数除法的意义,掌握求一个数的几分之几是多少和已知一个数的几分之几是多少,求这个数的计算方法,从而解决问题。
2.A
【分析】以荷花池为观测点,以图上的“上北下南,左西右东”为准,根据方向、角度和距离确定各选项中升旗台与荷花池的位置关系。
【解答】A.学校里的升旗台在荷花池的南偏西25°(或西偏南65°)方向200米处,符合题意;
B.学校里的升旗台在荷花池的北偏东25°(或东偏北65°)方向200米处,不符合题意;
C.学校里的升旗台在荷花池的南偏东25°(或东偏南65°)方向200米处,不符合题意。
故答案为:A
3.C
【分析】先表示出两人的工作效率,再用甲的工作效率除以乙的工作效率即可解答。
【解答】甲的工作效率:1÷4=
乙的工作效率:1÷5=
÷×100%
=×5×100%
=1.25×100%
=125%
甲的工效是乙的125%。
故答案为:C
【点评】本题也可根据完成相同的工作量,所用时间与效率成反比列式为:5÷4×100%=125%。
4.C
【分析】由图知道小圆的直径是大圆的半径,利用圆的周长公式C=2πr或πd分别求出半圆弧长,即可分别求得两个路径的长,然后进行比较即可。
【解答】设小圆的直径为d,则大圆的半径为d,
A路线的长度为:2πd÷2=πd,
B路线的长度为:πd÷2+πd÷2
=(πd+πd)÷2
=2πd÷2
=πd;
所以A、B两条路的长度一样长。
故答案为:C
【点评】本题主要是灵活利用圆的周长公式解决问题。
5.B
【分析】先用减法求出乙、丙两个数的和,丙数占乙、丙两个数和的,再用分数乘法求出丙数,据此解答。
【解答】(300-120)×
=180×
=108
所以,丙数是108。
故答案为:B
【点评】本题主要考查比的应用,求出乙、丙两个数的和与丙数占两数之和的分率是解答题目的关键。
6.C
【分析】根据题意,可以设两根铁丝的长度分别为1米、9米、0.9米进行讨论;
求第一根铁丝剩下的长度,把铁丝的全长看作单位“1”,甲用去全长的,则剩下的长度是全长的(1-),根据求一个数的几分之几是多少,用全长乘(1-),求出甲剩下的长度;
求乙剩下的长度,用全长减去米即可。
最后比较两根铁丝剩下的长度,得出结论。
【解答】(1)当两根铁丝都等于1米时;
甲剩下:
1×(1-)
=1×
=(米)
乙剩下:
1-=(米)
两根铁丝剩下的长度一样长。
(2)当两根铁丝的长度都大于1米时,假设是9米。
甲剩下:
9×(1-)
=9×
=6(米)
乙剩下:
9-=(米)
6<
乙铁丝剩下的长度长。
(3)当两根铁丝的长度都小于1米,大于米时,假设是0.9米。
甲剩下:
0.9×(1-)
=0.9×
=0.6(米)
乙剩下:
0.9-
=-
=-
=(米)
0.6==
>,所以0.6>;
甲铁丝剩下的长度长。
综上所述,这两根铁丝剩下的长度无法比较。
故答案为:C
【点评】区分“”和“米”的不同,从两根铁丝的长度分情况讨论,根据分数乘法的意义求出甲铁丝剩下的长度,根据减法的意义求出乙铁丝剩下的长度,再比较大小,得出不同的长度有不同的结果。
7.100;40;3.6;250
【分析】先计算出20÷8=2.5,根据小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分;则2.5=;根据分数的基本性质,将的分子和分母同时乘20,则=;将的分子和分母同时乘8,则=;根据分数和除法的关系,则=40÷16;已知比的前项是9,比值是2.5,根据比和除法的关系,可知比的后项为(9÷2.5);小数化为百分数,就是将小数点向右移动两位,再在小数的末尾加上百分号。
【解答】
【点评】本题考查了除法、分数、比和百分数的互化,关键是根据它们之间的性质和关系进行转化。
8. 乘 除 减
【分析】在混合运算中,先算乘除法,再算加减法;同级运算,应按照从左到右的运算顺序进行计算即可。观察算式-÷1.2,该算式的后半部分÷1.2属于同级运算,应先算乘法,再算除法,再加上前半部分,则最后算减法。
【解答】由分析可知:
计算综合算式:-÷1.2时,应该先算乘法,再算除法,最后算减法。
9. 东 北 30 400
【分析】隹观测点,以图上的“上北下南,左西右东”为准,图例表示图上1厘米相当于实际距离的100米,结合方向、角度和距离填空即可。
【解答】100×4=400(米)
丽丽要从学校沿东偏北30°(或北偏东60°)方向走400米去足球场训练。
10.白兔的只数;
【分析】白兔只数的相当于黑兔的只数,是把白兔的只数看作单位“1”,把它平均分成3份,黑兔的只数相当于1份;黑兔的只数比白兔的只数少。
【解答】
白兔只数的相当于黑兔的只数,这句话是把白兔的只数看作单位“1”;黑兔只数比白兔只数少。
11.25
【分析】比的前项和后项同时乘或除以相同的数(0除外),比值不变。给4∶5的前项加上20,相当于前项乘6,要使比值保持不变,后项要乘6。
【解答】4+20=24
24÷4=6
5×6-5
=30-5
=25
给4∶5的前项加上20,要使比值不变,比的后项应加上25。
【点评】本题主要考查了比的基本性质,熟练掌握比的基本性质是解题的关键。
12. 扇 90
【分析】由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形,分针相当于圆的半径;钟面一个大格是30度,据此分析。
【解答】30×3=90(度)
钟面上分针从12走到3,分针扫过的部分是个扇形,它的圆心角是90度。
【点评】关键是熟悉扇形的特征,扇形是圆的一部分。
13. 折线 扇形
【分析】条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况;扇形统计图特点:可以看出各个部分数量与总数之间的关系,据此结合题意选择合适的统计图。
【解答】每年的梅雨季节都是梁子湖的防汛期,为了观察这一期间的温度变化情况,应选用折线统计图;为了反映出这期间各类天气占总天数的百分比,应选用扇形统计图。
14.6
【分析】把这条公路的长度看作单位“1”,根据工作总量÷工作时间=工作效率,据此可知王师傅的工作效率为,最后根据工作总量÷工作效率之和=工作时间,据此解答即可。
【解答】1×50%÷(+)
=÷(+)
=÷
=×12
=6(天)
则两人合作,6天后完成这条公路的50%。
【点评】本题考查分数除法,明确工作总量、工作时间和工作效率之间的关系是解题的关键。
15.23.55
【分析】如图,羊能跑出的距离分别一个大扇形的弧长和两个小扇形的弧长,即三个不同半径圆的周长的,最后再相加即可。
【解答】2×3.14×8×+2×3.14×5×+2×3.14×2×
=50.24×+31.4×+12.56×
=(50.24+31.4+12.56)×
=94.2×
=23.55(m)
则最多可跑23.55m。
【点评】本题考查圆的周长,明确这只羊跑的路线是解题的关键。
16. 94cm2/94平方厘米 60cm3/60立方厘米
【分析】棱长和÷4=一组长宽高的和,长宽高的和÷总份数,求出一份数,一份数分别乘长、宽、高对应份数,求出长、宽、高,根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,列式计算即可。
【解答】48÷4÷(5+3+4)
=12÷12
=1(cm)
5×1=5(cm)
3×1=3(cm)
4×1=4(cm)
(5×3+5×4+3×4)×2
=(15+20+12)×2
=47×2
=94(cm2)
5×3×4=60(cm3)
这个长方体的表面积为94cm2,体积为60cm3。
【点评】关键是理解比的意义,掌握并灵活运用长方体表面积和体积公式。
17.9
【分析】将要组装的手表总数量看作工作总量,将工作总量看作单位“1”,时间分之一可以看作工作效率,两人效率和-徒弟工作效率=师父工作效率,工作总量÷师父工作效率=师父单独完成需要的天数,据此列式计算。
【解答】1÷(-)
=1÷
=1×9
=9(天)
师父单独完成需要9天。
18.41
【分析】根据规律,从1开始连续的几个奇数相加,就等于几的平方,即;据此解答。
【解答】根据分析:
将1+3+5+7+9+7+5+3+1分为1+3+5+7+9和;
25+16=41
所以1+3+5+7+9+7+5+3+1=41。
19.;;;;0.24
;3.5;;27;5
【解答】略
20.2;
;
【分析】第一小题是分数的乘除法混合运算,先计算括号里面的分数乘法,再计算括号外的分数除法,除以一个数等于乘这个数的倒数,可得出答案;
第二小题中先将分数除法化为乘法,可运用分数乘法的分配律提取公因数,进行简便运算得出答案;
第三小题中可根据分数乘法分配律去括号,进行简便运算;
第四小题先计算括号里面的减法,再计算分数除法,最后计算括号外面的分数乘法,据此可得出答案。
【解答】
21.;
【分析】(1)先计算左边的加法,再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以3.5,计算即可得解;
(2)先根据等式的基本性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时加上50%。再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以,计算即可得解。
【解答】
解:
解:
22.17.12平方厘米;14.13平方厘米
【分析】(1)根据第一个图形示,求阴影部分面积,阴影部分面积=半圆面积-三角形面积,三角形其中2个角顶点都在圆上,可以理解为圆半径,图中的三角形为直角三角形,那么图中2个在圆上的角顶点连接至圆形的线段,则可以看作三角形的底和高,根据三角形的面积公式:三角形面积=底×高÷2,半圆面积=πr2÷2。
(2)根据第二个图形示,求的是圆环的面积,根据圆环面积公式:圆环面积=π(R2-r2),因为是半圆环形面积,将得出圆环面积÷2即可,将数据代入计算出结果即可。
【解答】(1)8÷2=4(厘米)
3.14×42÷2=25.12(平方厘米)
4×4÷2=8(平方厘米)
25.12-8=17.12(平方厘米)
阴影部分面积为:17.12平方厘米
(2)3.14×(52-42)÷2
=3.14×(25-16)÷2
=28.26÷2
=14.13(平方厘米)
阴影部分的面积为:14.13平方厘米
23.见解答
【分析】弄清要标示的物体在哪个方位上,有多少度,按要求的方位和度数准确画图;注意各场所离中心点的距离,根据要求画出相应的长度。
【解答】
24.(1)1200个;图见解答
(2)66.7%
【分析】(1)从两幅图中可知,C品牌销售1800个占销售总个数的50%,把销售总个数看作单位“1”,单位“1”未知,用C品牌的销售个数除以50%,即可求出总个数;
再用总个数减去A、C品牌的销售个数,即是B品牌的销售个数,据此将条形统计图补充完整。
(2)从条形统计图中可知,A品牌销售600个,C品牌销售1800个,求A品牌的销售个数比C品牌少百分之几,先用减法求出少的个数,再除以C品牌的销售个数即可。
【解答】(1)总个数:
1800÷50%
=1800÷0.5
=3600(个)
B品牌:3600-600-1800=1200(个)
答:B品牌粽子销售1200个。
如图:
(2)(1800-600)÷1800×100%
=1200÷1800×100%
≈0.667×100%
=66.7%
答:A品牌的销售个数比C品牌少66.7%。
25.140吨
【分析】将每天收到的生活垃圾吨数看作单位“1”,每天收到的生活垃圾吨数×可回收利用的垃圾对应分率=每天可回收利用的垃圾吨数,一周是7天,每天可回收利用的垃圾吨数×7即可。
【解答】60××7
=20×7
=140(吨)
答:这个垃圾处理厂一周收到的垃圾中有140吨可回收利用。
【点评】关键是确定单位“1”,理解分数乘法的意义。
26.270个
【分析】将六二班的跳绳数量看作单位“1”,单位“1”未知,用六一班跳绳数量除以求出六二班的跳绳数量。根据比可知,六三班跳绳数量是六二班的,那么将六二班跳绳数量乘,即可求出六三班的跳绳数量。
【解答】280÷×
=280××
=240×
=270(个)
答:六三班跳了270个。
27.推理过程见解答
选射程为15米的装置合适,灌溉面积接近700平方米,安装在中心位置。
【分析】根据圆的面积=×半径的平方,分别求出半径是15米和半径是10米的圆的面积,与700平方米最接近的即为所求。
【解答】3.14×
=3.14×225
=706.5(平方米)
3.14×
=3.14×100
=314(平方米)
706.5平方米更接近700平方米。
答:射程是15米的自动旋转喷灌装置,灌溉面积接近700平方米,把它安装在安装在中心位置。
28.6天
【分析】把这批订单看作单位“1”,根据工作效率=工作总量÷工作时间,用1÷10,求出第一车间的工作效率;第二车间单独做3天完成了,用÷3,求出第二车间的工作效率,再根据工作时间=工作总量÷工作效率,用1除以第一车间与第二车间的工作效率和,即可解答。
【解答】1÷(+÷3)
=1÷(+×)
=1÷(+)
=1÷(+)
=1÷
=1×
=6(天)
答:6天可以完成这批订单。
29.600棵
【分析】根据题意,六年级一共种植了2000棵,超额完成分配任务的25%,把六年级分配任务的棵数看作单位“1”,则六年级实际种植的棵数是分配任务的(1+25%),单位“1”未知,用六年级实际种植的棵数除以(1+25%),求出六年级分配任务的棵数;
已知这批树苗按5∶8分配给五、六年级,即分配给五年级的棵数占5份,分配给六年级的棵数占8份;用六年级分配任务的棵数除以8,求出一份数,再用一份数乘5,即是五年级分配树苗的棵数;
已知五年级同学只完成了分配任务的60%,把五年级分配任务的棵数看作单位“1”,根据求一个数的百分之几是多少,用五年级分配任务的棵数乘60%,即可求出五年级实际种植的棵数。
【解答】六年级分配树苗的棵数:
2000÷(1+25%)
=2000÷1.25
=1600(棵)
五年级分配树苗的棵数:
1600÷8×5
=200×5
=1000(棵)
五年级同学实际种植:
1000×60%
=1000×0.6
=600(棵)
答:五年级同学实际种植了600棵。
【点评】本题考查百分数乘除法的实际应用以及比的应用,关键是分清两个不同的单位“1”,单位“1”已知,根据百分数乘法的意义解答;单位“1”未知,根据百分数除法的意义解答。
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个数的是36的,这个数是( )。
A.60 B.50 C.30
2.学校里的升旗台在荷花池的南偏西25°方向200米处,下面图( )符合这句话的描述。
A. B. C.
3.做一个零件,甲要4分钟完成,乙要5分钟完成,甲的工效是乙的( )。
A.80% B.120% C.125%
4.如下图,从甲地到乙地,A、B两条路线的长度相比,( )。
A.A长一些 B.B长一些 C.一样长
5.甲、乙、丙三个数的和是300,甲数是120,乙数与丙数的比是2∶3,丙数是( )。
A.72 B.108 C.180
6.甲乙两根同样长的铁丝,甲用去,乙用去米,剩下的长度比较,( )。
A.甲长 B.乙长 C.无法确定哪根长
二、填空题
7.。
8.计算综合算式:-÷1.2时,应该先算( )法,再算( )法,最后算( )法。
9.如图:丽丽要从学校沿( 偏 )( )°方向走( )米去足球场训练。
10.白兔只数的相当于黑兔的只数,这句话是把( )看作单位“1”;黑兔只数比白兔只数少。
11.给4∶5的前项加上20,要使比值不变,比的后项应加上( )。
12.钟面上分针从12走到3,分针扫过的部分是个( )形,它的圆心角是( )度。
13.每年的梅雨季节都是梁子湖的防汛期,为了观察这一期间的温度变化情况,应选用( )统计图;为了反映出这期间各类天气占总天数的百分比,应选用( )统计图。
14.修一条公路,王师傅单独工作需要20天完成,李师傅每天修整条公路的,如两人合作,( )天后完成这条公路的50%。
15.有一只羊被拴在一间底面边长为3m正方形小房子的墙角B点(如下图),拴羊的绳子长8m,这只羊从A点出发,将绳子拉紧顺时针跑,最多可跑( )m。
16.一个长方体的棱长和是48cm,长、宽、高的比是5∶3∶4,这个长方体的表面积为( ),体积为( )。
17.要组装一批手表,如果徒弟单独完成需要18天,而师父与徒弟合作需要6天可以完成,那么师父单独完成需要( )天。
18.根据下面的规律,算一算。
1+3+5+7+9+7+5+3+1=( )。
三、计算题
19.直接写得数。
×5= ×= ÷= ÷4= 0.3×80%=
4.2×= +=
20.看清题目,细心计算。(下面各题怎样算简便就怎样算。)
21.解方程。
22.我会计算下面图形阴影部分的面积。(单位:cm)
四、作图题
23.根据下面的描述,在平面图上画出各动物场馆的位置。
(1)海豚馆在动物园大门的西偏南60°方向300米处。
(2)大象馆在动物园大门的北偏东30°方向400米处。
(3)熊猫馆在动物园大门的正西方向100米处。
五、解答题
24.某商场对今年端午节这天的A、B、C三种品牌的粽子销售情况进行统计。
(1)列式求出B品牌粽子销售的个数,将条形统计图补充完整。
(2)A品牌的销售个数比C品牌少百分之几?(百分号前保留一位小数)
25.一个垃圾处理厂平均每天收到60吨生活垃圾,其中可回收利用的垃圾占,这个垃圾处理厂一周收到的垃圾中有多少吨可回收利用?
26.在运动会的“8字跳绳”比赛中,六一班跳绳数量是六二班的,六三班与六二班的比是9∶8,六一班共跳280个,你知道六三班跳了多少个吗?
27.儿童广场里有一块面积为700平方米的圆形草坪,要在草坪上安装一个自动旋转喷灌装置进行喷灌。现在有射程是15米和10米的两种装置,你认为应该选哪种装置比较合适?你打算把它安装在什么位置?请写出推理过程。
28.服装厂接到一批订单,第一车间单独做需要10天完成,第二车间单独做3天完成了,如果两个车间同时做这批订单,多少天可以完成这批订单?
29.实验小学组织五、六年级的同学种一批树苗,把这批树苗按5∶8分配给五、六年级。植树结束后,李老师发现:六年级同学完成分配任务后,又帮助五年级同学种植了一些正好一共种植了2000棵,超额完成分配任务的25%,而五年级同学只完成了分配任务的60%。五年级同学实际种植了多少棵?
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据分数乘法的意义,求一个数的几分之几是多少,用乘法,用36乘求出结果为30。再根据分数除法的意义,已知一个数的几分之几是多少,求这个数,用除法,用30除以,即可求出这个数。
【解答】36×÷
=30÷
=30×
=50
即这个数是50。
故答案为:B
【点评】此题的解题关键是理解分数乘法和分数除法的意义,掌握求一个数的几分之几是多少和已知一个数的几分之几是多少,求这个数的计算方法,从而解决问题。
2.A
【分析】以荷花池为观测点,以图上的“上北下南,左西右东”为准,根据方向、角度和距离确定各选项中升旗台与荷花池的位置关系。
【解答】A.学校里的升旗台在荷花池的南偏西25°(或西偏南65°)方向200米处,符合题意;
B.学校里的升旗台在荷花池的北偏东25°(或东偏北65°)方向200米处,不符合题意;
C.学校里的升旗台在荷花池的南偏东25°(或东偏南65°)方向200米处,不符合题意。
故答案为:A
3.C
【分析】先表示出两人的工作效率,再用甲的工作效率除以乙的工作效率即可解答。
【解答】甲的工作效率:1÷4=
乙的工作效率:1÷5=
÷×100%
=×5×100%
=1.25×100%
=125%
甲的工效是乙的125%。
故答案为:C
【点评】本题也可根据完成相同的工作量,所用时间与效率成反比列式为:5÷4×100%=125%。
4.C
【分析】由图知道小圆的直径是大圆的半径,利用圆的周长公式C=2πr或πd分别求出半圆弧长,即可分别求得两个路径的长,然后进行比较即可。
【解答】设小圆的直径为d,则大圆的半径为d,
A路线的长度为:2πd÷2=πd,
B路线的长度为:πd÷2+πd÷2
=(πd+πd)÷2
=2πd÷2
=πd;
所以A、B两条路的长度一样长。
故答案为:C
【点评】本题主要是灵活利用圆的周长公式解决问题。
5.B
【分析】先用减法求出乙、丙两个数的和,丙数占乙、丙两个数和的,再用分数乘法求出丙数,据此解答。
【解答】(300-120)×
=180×
=108
所以,丙数是108。
故答案为:B
【点评】本题主要考查比的应用,求出乙、丙两个数的和与丙数占两数之和的分率是解答题目的关键。
6.C
【分析】根据题意,可以设两根铁丝的长度分别为1米、9米、0.9米进行讨论;
求第一根铁丝剩下的长度,把铁丝的全长看作单位“1”,甲用去全长的,则剩下的长度是全长的(1-),根据求一个数的几分之几是多少,用全长乘(1-),求出甲剩下的长度;
求乙剩下的长度,用全长减去米即可。
最后比较两根铁丝剩下的长度,得出结论。
【解答】(1)当两根铁丝都等于1米时;
甲剩下:
1×(1-)
=1×
=(米)
乙剩下:
1-=(米)
两根铁丝剩下的长度一样长。
(2)当两根铁丝的长度都大于1米时,假设是9米。
甲剩下:
9×(1-)
=9×
=6(米)
乙剩下:
9-=(米)
6<
乙铁丝剩下的长度长。
(3)当两根铁丝的长度都小于1米,大于米时,假设是0.9米。
甲剩下:
0.9×(1-)
=0.9×
=0.6(米)
乙剩下:
0.9-
=-
=-
=(米)
0.6==
>,所以0.6>;
甲铁丝剩下的长度长。
综上所述,这两根铁丝剩下的长度无法比较。
故答案为:C
【点评】区分“”和“米”的不同,从两根铁丝的长度分情况讨论,根据分数乘法的意义求出甲铁丝剩下的长度,根据减法的意义求出乙铁丝剩下的长度,再比较大小,得出不同的长度有不同的结果。
7.100;40;3.6;250
【分析】先计算出20÷8=2.5,根据小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分;则2.5=;根据分数的基本性质,将的分子和分母同时乘20,则=;将的分子和分母同时乘8,则=;根据分数和除法的关系,则=40÷16;已知比的前项是9,比值是2.5,根据比和除法的关系,可知比的后项为(9÷2.5);小数化为百分数,就是将小数点向右移动两位,再在小数的末尾加上百分号。
【解答】
【点评】本题考查了除法、分数、比和百分数的互化,关键是根据它们之间的性质和关系进行转化。
8. 乘 除 减
【分析】在混合运算中,先算乘除法,再算加减法;同级运算,应按照从左到右的运算顺序进行计算即可。观察算式-÷1.2,该算式的后半部分÷1.2属于同级运算,应先算乘法,再算除法,再加上前半部分,则最后算减法。
【解答】由分析可知:
计算综合算式:-÷1.2时,应该先算乘法,再算除法,最后算减法。
9. 东 北 30 400
【分析】隹观测点,以图上的“上北下南,左西右东”为准,图例表示图上1厘米相当于实际距离的100米,结合方向、角度和距离填空即可。
【解答】100×4=400(米)
丽丽要从学校沿东偏北30°(或北偏东60°)方向走400米去足球场训练。
10.白兔的只数;
【分析】白兔只数的相当于黑兔的只数,是把白兔的只数看作单位“1”,把它平均分成3份,黑兔的只数相当于1份;黑兔的只数比白兔的只数少。
【解答】
白兔只数的相当于黑兔的只数,这句话是把白兔的只数看作单位“1”;黑兔只数比白兔只数少。
11.25
【分析】比的前项和后项同时乘或除以相同的数(0除外),比值不变。给4∶5的前项加上20,相当于前项乘6,要使比值保持不变,后项要乘6。
【解答】4+20=24
24÷4=6
5×6-5
=30-5
=25
给4∶5的前项加上20,要使比值不变,比的后项应加上25。
【点评】本题主要考查了比的基本性质,熟练掌握比的基本性质是解题的关键。
12. 扇 90
【分析】由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形,分针相当于圆的半径;钟面一个大格是30度,据此分析。
【解答】30×3=90(度)
钟面上分针从12走到3,分针扫过的部分是个扇形,它的圆心角是90度。
【点评】关键是熟悉扇形的特征,扇形是圆的一部分。
13. 折线 扇形
【分析】条形统计图特点:可以清楚地看出数量的多少;折线统计图特点:不但可以表示数量的多少,还可以清楚的看出数量的增减变化情况;扇形统计图特点:可以看出各个部分数量与总数之间的关系,据此结合题意选择合适的统计图。
【解答】每年的梅雨季节都是梁子湖的防汛期,为了观察这一期间的温度变化情况,应选用折线统计图;为了反映出这期间各类天气占总天数的百分比,应选用扇形统计图。
14.6
【分析】把这条公路的长度看作单位“1”,根据工作总量÷工作时间=工作效率,据此可知王师傅的工作效率为,最后根据工作总量÷工作效率之和=工作时间,据此解答即可。
【解答】1×50%÷(+)
=÷(+)
=÷
=×12
=6(天)
则两人合作,6天后完成这条公路的50%。
【点评】本题考查分数除法,明确工作总量、工作时间和工作效率之间的关系是解题的关键。
15.23.55
【分析】如图,羊能跑出的距离分别一个大扇形的弧长和两个小扇形的弧长,即三个不同半径圆的周长的,最后再相加即可。
【解答】2×3.14×8×+2×3.14×5×+2×3.14×2×
=50.24×+31.4×+12.56×
=(50.24+31.4+12.56)×
=94.2×
=23.55(m)
则最多可跑23.55m。
【点评】本题考查圆的周长,明确这只羊跑的路线是解题的关键。
16. 94cm2/94平方厘米 60cm3/60立方厘米
【分析】棱长和÷4=一组长宽高的和,长宽高的和÷总份数,求出一份数,一份数分别乘长、宽、高对应份数,求出长、宽、高,根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,列式计算即可。
【解答】48÷4÷(5+3+4)
=12÷12
=1(cm)
5×1=5(cm)
3×1=3(cm)
4×1=4(cm)
(5×3+5×4+3×4)×2
=(15+20+12)×2
=47×2
=94(cm2)
5×3×4=60(cm3)
这个长方体的表面积为94cm2,体积为60cm3。
【点评】关键是理解比的意义,掌握并灵活运用长方体表面积和体积公式。
17.9
【分析】将要组装的手表总数量看作工作总量,将工作总量看作单位“1”,时间分之一可以看作工作效率,两人效率和-徒弟工作效率=师父工作效率,工作总量÷师父工作效率=师父单独完成需要的天数,据此列式计算。
【解答】1÷(-)
=1÷
=1×9
=9(天)
师父单独完成需要9天。
18.41
【分析】根据规律,从1开始连续的几个奇数相加,就等于几的平方,即;据此解答。
【解答】根据分析:
将1+3+5+7+9+7+5+3+1分为1+3+5+7+9和;
25+16=41
所以1+3+5+7+9+7+5+3+1=41。
19.;;;;0.24
;3.5;;27;5
【解答】略
20.2;
;
【分析】第一小题是分数的乘除法混合运算,先计算括号里面的分数乘法,再计算括号外的分数除法,除以一个数等于乘这个数的倒数,可得出答案;
第二小题中先将分数除法化为乘法,可运用分数乘法的分配律提取公因数,进行简便运算得出答案;
第三小题中可根据分数乘法分配律去括号,进行简便运算;
第四小题先计算括号里面的减法,再计算分数除法,最后计算括号外面的分数乘法,据此可得出答案。
【解答】
21.;
【分析】(1)先计算左边的加法,再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以3.5,计算即可得解;
(2)先根据等式的基本性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时加上50%。再根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以,计算即可得解。
【解答】
解:
解:
22.17.12平方厘米;14.13平方厘米
【分析】(1)根据第一个图形示,求阴影部分面积,阴影部分面积=半圆面积-三角形面积,三角形其中2个角顶点都在圆上,可以理解为圆半径,图中的三角形为直角三角形,那么图中2个在圆上的角顶点连接至圆形的线段,则可以看作三角形的底和高,根据三角形的面积公式:三角形面积=底×高÷2,半圆面积=πr2÷2。
(2)根据第二个图形示,求的是圆环的面积,根据圆环面积公式:圆环面积=π(R2-r2),因为是半圆环形面积,将得出圆环面积÷2即可,将数据代入计算出结果即可。
【解答】(1)8÷2=4(厘米)
3.14×42÷2=25.12(平方厘米)
4×4÷2=8(平方厘米)
25.12-8=17.12(平方厘米)
阴影部分面积为:17.12平方厘米
(2)3.14×(52-42)÷2
=3.14×(25-16)÷2
=28.26÷2
=14.13(平方厘米)
阴影部分的面积为:14.13平方厘米
23.见解答
【分析】弄清要标示的物体在哪个方位上,有多少度,按要求的方位和度数准确画图;注意各场所离中心点的距离,根据要求画出相应的长度。
【解答】
24.(1)1200个;图见解答
(2)66.7%
【分析】(1)从两幅图中可知,C品牌销售1800个占销售总个数的50%,把销售总个数看作单位“1”,单位“1”未知,用C品牌的销售个数除以50%,即可求出总个数;
再用总个数减去A、C品牌的销售个数,即是B品牌的销售个数,据此将条形统计图补充完整。
(2)从条形统计图中可知,A品牌销售600个,C品牌销售1800个,求A品牌的销售个数比C品牌少百分之几,先用减法求出少的个数,再除以C品牌的销售个数即可。
【解答】(1)总个数:
1800÷50%
=1800÷0.5
=3600(个)
B品牌:3600-600-1800=1200(个)
答:B品牌粽子销售1200个。
如图:
(2)(1800-600)÷1800×100%
=1200÷1800×100%
≈0.667×100%
=66.7%
答:A品牌的销售个数比C品牌少66.7%。
25.140吨
【分析】将每天收到的生活垃圾吨数看作单位“1”,每天收到的生活垃圾吨数×可回收利用的垃圾对应分率=每天可回收利用的垃圾吨数,一周是7天,每天可回收利用的垃圾吨数×7即可。
【解答】60××7
=20×7
=140(吨)
答:这个垃圾处理厂一周收到的垃圾中有140吨可回收利用。
【点评】关键是确定单位“1”,理解分数乘法的意义。
26.270个
【分析】将六二班的跳绳数量看作单位“1”,单位“1”未知,用六一班跳绳数量除以求出六二班的跳绳数量。根据比可知,六三班跳绳数量是六二班的,那么将六二班跳绳数量乘,即可求出六三班的跳绳数量。
【解答】280÷×
=280××
=240×
=270(个)
答:六三班跳了270个。
27.推理过程见解答
选射程为15米的装置合适,灌溉面积接近700平方米,安装在中心位置。
【分析】根据圆的面积=×半径的平方,分别求出半径是15米和半径是10米的圆的面积,与700平方米最接近的即为所求。
【解答】3.14×
=3.14×225
=706.5(平方米)
3.14×
=3.14×100
=314(平方米)
706.5平方米更接近700平方米。
答:射程是15米的自动旋转喷灌装置,灌溉面积接近700平方米,把它安装在安装在中心位置。
28.6天
【分析】把这批订单看作单位“1”,根据工作效率=工作总量÷工作时间,用1÷10,求出第一车间的工作效率;第二车间单独做3天完成了,用÷3,求出第二车间的工作效率,再根据工作时间=工作总量÷工作效率,用1除以第一车间与第二车间的工作效率和,即可解答。
【解答】1÷(+÷3)
=1÷(+×)
=1÷(+)
=1÷(+)
=1÷
=1×
=6(天)
答:6天可以完成这批订单。
29.600棵
【分析】根据题意,六年级一共种植了2000棵,超额完成分配任务的25%,把六年级分配任务的棵数看作单位“1”,则六年级实际种植的棵数是分配任务的(1+25%),单位“1”未知,用六年级实际种植的棵数除以(1+25%),求出六年级分配任务的棵数;
已知这批树苗按5∶8分配给五、六年级,即分配给五年级的棵数占5份,分配给六年级的棵数占8份;用六年级分配任务的棵数除以8,求出一份数,再用一份数乘5,即是五年级分配树苗的棵数;
已知五年级同学只完成了分配任务的60%,把五年级分配任务的棵数看作单位“1”,根据求一个数的百分之几是多少,用五年级分配任务的棵数乘60%,即可求出五年级实际种植的棵数。
【解答】六年级分配树苗的棵数:
2000÷(1+25%)
=2000÷1.25
=1600(棵)
五年级分配树苗的棵数:
1600÷8×5
=200×5
=1000(棵)
五年级同学实际种植:
1000×60%
=1000×0.6
=600(棵)
答:五年级同学实际种植了600棵。
【点评】本题考查百分数乘除法的实际应用以及比的应用,关键是分清两个不同的单位“1”,单位“1”已知,根据百分数乘法的意义解答;单位“1”未知,根据百分数除法的意义解答。
同课章节目录
