人教版八年级数学上册能力提升复习题(含详解)
文档属性
| 名称 | 人教版八年级数学上册能力提升复习题(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 893.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 00:00:00 | ||
图片预览




文档简介
人教版八年级数学上册能力提升复习题
考试范围:人教版八年级数学上册;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
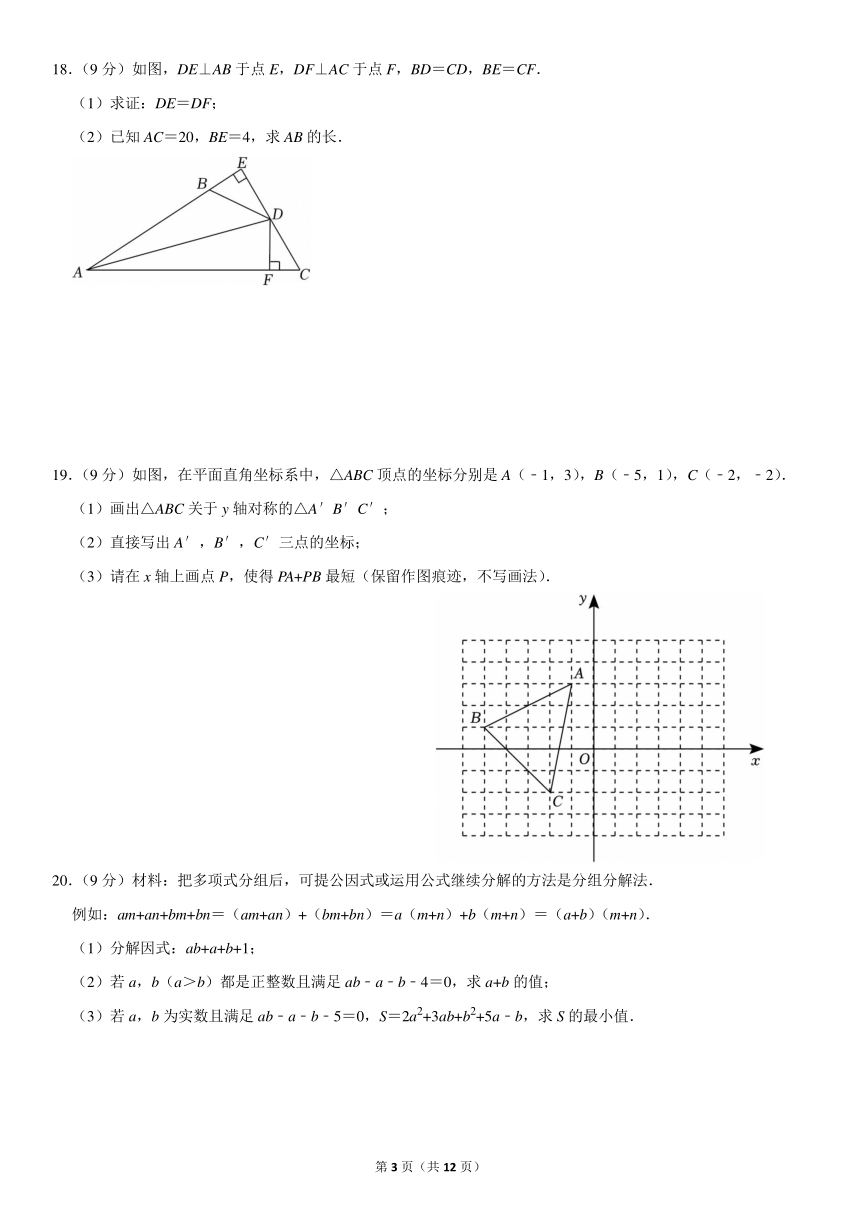
一.选择题(共10小题,满分30分,每小题3分)
1.下列分式中,是最简分式的是( )
A. B. C. D.
2.计算:(﹣2m4)3=( )
A.﹣6m7 B.﹣8m7 C.﹣2m12 D.﹣8m12
3.下列运算正确的是( )
A.(a+b)2=a2+b2 B.a2×a3=a6 C.(a﹣b)(b﹣a)=a2﹣b2 D.(a2)3=a6
4.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS B.AAS C.ASA D.SAS
5.若4x2+kx+9是一个完全平方式,则m的取值是( )
A.±12 B.12 C.±6 D.6
6.如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,若AC=14,且AD:DC=4:3,则点D到AB的距离DE是( )
A.3 B.4 C.5 D.6
7.如图,五边形ABCDE的内角都相等,且∠ADE=∠DAE,∠BDC=∠DBC,则∠ADB=( )
A.18° B.36° C.72° D.108°
8.等腰三角形两边长分别为2和4,则这个等腰三角形的周长为( )
A.6 B.8 C.10 D.8或10
9.如图,在△ABC中,AB=AC,∠A=30°,取大于的长为半径,分别以点A、B为圆心,作弧相交于两点,过此两点的直线交AC边于点D(作图痕迹如图所示),连接BD,则∠DBC的度数为( )
A.30° B.45° C.60° D.75°
10.一个正多边形的外角与其相邻的内角的度数之比为2:7,那么这个多边形的边数为( )
A.8 B.9 C.10 D.12
二.填空题(共5小题,满分15分,每小题3分)
11.计算:20200+()﹣1= .
12.若关于x的分式方程无解,则a的值为 .
13.已知a+b=﹣5,ab=6,则a2+b2= .
14.如图,CE平分∠ACD,交AB于点E,若∠A=40°,∠B=30°,∠BDC=110°,则∠BEC的度数为 .
15.如图,在△ABC中,∠ACB=60°,点D在AB上,CD=14,∠BDC=60°,延长CB至点E,使CE=AC,过点E作EF⊥CD于点F,交AB于点G,若2DG=AD,则DF= .
(14题图) (15题图)
三.解答题(共8小题,满分75分)
16.(10分)(1)计算:(4x+1)(x﹣2)﹣(2x﹣3)2; (2)解方程:.
17.(8分)先化简再求值:(1),再从0,﹣1,2中选一个数作为a的值代入求值.
18.(9分)如图,DE⊥AB于点E,DF⊥AC于点F,BD=CD,BE=CF.
(1)求证:DE=DF;
(2)已知AC=20,BE=4,求AB的长.
19.(9分)如图,在平面直角坐标系中,△ABC顶点的坐标分别是A(﹣1,3),B(﹣5,1),C(﹣2,﹣2).
(1)画出△ABC关于y轴对称的△A′B′C′;
(2)直接写出A′,B′,C′三点的坐标;
(3)请在x轴上画点P,使得PA+PB最短(保留作图痕迹,不写画法).
20.(9分)材料:把多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(a+b)(m+n).
(1)分解因式:ab+a+b+1;
(2)若a,b(a>b)都是正整数且满足ab﹣a﹣b﹣4=0,求a+b的值;
(3)若a,b为实数且满足ab﹣a﹣b﹣5=0,S=2a2+3ab+b2+5a﹣b,求S的最小值.
21.(9分)如图,AE⊥DB,CF⊥DB,垂足分别是点E,F,DE=BF,AB=CD.
求证:∠A=∠C.
22.(10分)受疫情影响,“84”消毒液需求量猛增,某商场用8000元购进一批“84”消毒液后,供不应求,商场用17600元购进第二批这种“84”消毒液,所购数量是第一批数量的2倍,但单价贵了1元.
(1)求该商场购进的第一批“84”消毒液的单价;
(2)商场销售这种“84”消毒液时,每瓶定价为13元,最后200瓶按9折销售,很快售完,在这两笔生意中商场共获利多少元?
23.(11分)如图,已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).
(1)如图1,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图3中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D A D B C B B
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、,不是最简分式,不符合题意;
B、,不是最简分式,不符合题意;
C、是最简分式,符合题意;
D、1,不是最简分式,不符合题意;
选:C.
2.解:(﹣2m4)3=(﹣2)3×(m4)3=﹣8m12,
选:D.
3.解:∵(a+b)2=a2+2ab+b2,选项A错误;
∵a2×a3=a5,选项B错误;
∵(a﹣b)(b﹣a)=﹣a2+2ab﹣b2,选项C错误;
∵(a2)3=a6,选项D正确;
选:D.
4.证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS).
选:D.
5.解:∵4x2+kx+9=(2x)2+kx+32,
∴kx=±2 2x 3,
解得:k=±12.
选:A.
6.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,BD平分∠ABC,
∴DE=CD,
∵AC=14,且AD:DC=4:3,
∴DC=146,
∴DE=CD=6,
即点D到AB的距离DE等于6,
选:D.
7.解:∵五边形ABCDE的内角都相等,
∴∠BAE=∠ABC=∠EDC=∠C=∠E=(5﹣2)×180°÷5=108°,
∴∠ADE=∠DAE=(180°﹣108°)÷2=36°,
∴∠DAB=∠BE﹣∠DAE=72°,
∠BDC=∠DBC=72°,
∴∠ADB=180°﹣∠DAB﹣∠DBA=36°.
选:B.
8.解:①2是腰长时,三角形的三边分别为2、2、4,
∵2+2=4,
∴不能组成三角形;
②2是底边时,三角形的三边分别为2、4、4,
能组成三角形,
周长=2+4+4=10,
综上所述,三角形的周长为10.
选:C.
9.解:由题意得,点D在线段AB的垂直平分线上,
∴AD=BD,
∴∠DBA=∠A=30°,
∵AB=AC,
∴,
∴∠DBC=∠ABC﹣∠DBA=45°,
选:B.
10.解:设正多边形的每个外角的度数为2x,与它相邻的内角的度数为7x,依题意有:
2x+7x=180°,
解得x=20°,
这个多边形的边数=360°÷40°=9.
选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:原式=1+3=4,
答案为:4.
12.解:,
3x+9+ax=4x﹣12,
(a﹣1)x=﹣21,
∵分式方程无解,
∴分两种情况:
当a﹣1=0时,a=1,
当(x+3)(x﹣3)=0时,x=±3,
把x=±3分别代入(a﹣1)x=﹣21中,
得a=8或﹣6,
综上所述:a的值为1或8或﹣6.
答案为:1或8或﹣6.
13.解:∵a+b=﹣5,
∴(a+b)2=25,
∴a2+2ab+b2=25.
∵ab=6,
∴a2+b2+12=25,
∴a2+b2=13.
答案为:13.
14.解:作射线AD,如图,
由三角形外角的性质得到:∠BDC=∠BDF+∠CDF=∠BAD+∠B+∠CAD+∠ACD=∠BAC+∠B+∠ACD,
又∵∠BAC=40°,∠B=30°,∠BDC=110°,
则∠ACD=∠BDC﹣∠BAC﹣∠B=110°﹣40°﹣30°=40°,
∵CE平分∠ACD,
∴,
∴∠BEC=∠BAC+∠ACE=40°+20°=60°,
即∠BEC=60°.
答案为:60°.
15.解:过点C作CH⊥AB于点H,如图所示:
设DF=x,
∵CD=14,
∴CF=CD﹣DF=14﹣x,
∵EF⊥CD,
在Rt△DFG中,∠BDC=60°,
∴∠DGF=30°,
∴DG=2DF=2x,
∵2DG=AD,
∴AD=2DG=4x,
∵CH⊥AB,
在Rt△CHD中,∠BDC=60°,
∴∠DCH=30°,
∴DHCD=7,
∴AH=AD+DH=4x+7,
∵∠BDC=∠A+∠ACD=60°,∠ACB=∠ACD+∠FCE=60°,
∴∠A=∠FCE,
又∵CH⊥AB,EF⊥CD,
∴∠AHC=∠CFE=90°,
在△ACH和△CFE中,
,
∴△ACH≌△CFE(AAS),
∴AH=CF,
∴4x+7=14﹣x,
解得:x.
答案为:.
三.解答题(共8小题,满分75分)
16.解:(1)原式=4x2﹣8x+x﹣2﹣(4x2﹣12x+9)
=4x2﹣8x+x﹣2﹣4x2+12x﹣9
=5x﹣11;
(2)去分母得:x(x+2)﹣x2+4=2,
解答:x=﹣1,
检验:把x=﹣1代入得:(x+2)(x﹣2)≠0,
∴分式方程的解为x=﹣1.
17.解:(1)
,
∵当a=﹣1或2时,原分式无意义,
∴a=0,
当a=0时,原式.
18.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中,BD=CD,BE=CF,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
(2)解:在Rt△BED和Rt△CFD中,AE=DF,AD=AD,
∴Rt△ADE≌Rt△ADF(HL),
∵△ADE≌△ADF,Rt△BED≌Rt△CFD,
∴AE=AF,CF=BE=4,
∵AC=20,
∴AE=AF=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.
19.(1)解:如图所示,△A′B′C′即为所求,
(2)解:由图知A′(1,3),B′(5,1),C′(2,﹣2);
(3)解:如图所示,点P即为所求.
20.解:(1)ab+a+b+1
=(ab+a)+(b+1)
=a(b+1)+(b+1)
=(a+1)(b+1);
(2)由题得ab﹣a﹣b+1=5,即(a﹣1)(b﹣1)=5,
∵a,b为正整数且a>b,
∴,即,
∴a+b=8;
(2)由题得ab=a+b+5,
S=2a2+3ab+b2+5a﹣b
=2a2+3a+3b+15+b2+5a﹣b
=2a2+8a+b2+2b+15
=2(a2+4a+4)+(b2+2b+1)+6
=2(a+2)2+(b+1)2+6,
∵(a+2)2≥0,(b+1)2≥0,
∴S≥6,(当且仅当a=﹣2,b=﹣1时取等号),
经验证:a=﹣2,b=﹣1满足ab﹣a﹣b﹣5=0,
综上,S的最小值为6.
21.证明:∵AE⊥DB,CF⊥DB,
∴∠AEB=∠CFD=90°,
∵DE=BF,
∴DF=BE,
在Rt△ABE和Rt△CDF中,
∴Rt△ABE≌Rt△CDF(HL),
∴∠A=∠C.
22.解:(1)设该商场购进的第一批“84”消毒液单价为x元/瓶,依题意得:2.
解得,x=10.
经检验,x=10是原方程的根.
所以该商场购进的第一批消毒液的单价为10元/瓶;
(2)共获利:(200)×13+200×13×0.9﹣(8000+17600)=5340(元).
在这两笔生意中商场共获得5340元.
23.解:(1)判断:EN与MF相等(或EN=MF),点F在直线NE上,
(2)成立.
延长EN交BC于点F,连接DF,
∵△ABC是等边三角形,
∴AB=AC=BC.
∵DMN为等边三角形,DM=DN,
又∵D,E,F是三边的中点,
∴EF=DF=BF,则BD=DF,
∵∠BDM+∠MDF=60°,∠FDN+∠MDF=60°,
∴∠BDM=∠FDN,
在△DBM和△DFN中,
,
∴△DBM≌△DFN(SAS),
∴BM=FN,∠DFN=∠FDB=60°,
∴NF∥BD,
∵E,F分别为边AC,BC的中点,
∴EF是△ABC的中位线,
∴EF∥BD,
∴F在直线NE上,
∵BF=EF,
∴MF=EN.
(3)如图③,MF与EN相等的结论仍然成立(或MF=NE成立).
连接DF、DE,
由(2)知DE=DF,∠NDE=∠FDM,DN=DM,
在△DNE和△DMF中,
∴△DNE≌△DMF(SAS),
∴MF=NE.
第12页(共12页)
考试范围:人教版八年级数学上册;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
一.选择题(共10小题,满分30分,每小题3分)
1.下列分式中,是最简分式的是( )
A. B. C. D.
2.计算:(﹣2m4)3=( )
A.﹣6m7 B.﹣8m7 C.﹣2m12 D.﹣8m12
3.下列运算正确的是( )
A.(a+b)2=a2+b2 B.a2×a3=a6 C.(a﹣b)(b﹣a)=a2﹣b2 D.(a2)3=a6
4.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS B.AAS C.ASA D.SAS
5.若4x2+kx+9是一个完全平方式,则m的取值是( )
A.±12 B.12 C.±6 D.6
6.如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,若AC=14,且AD:DC=4:3,则点D到AB的距离DE是( )
A.3 B.4 C.5 D.6
7.如图,五边形ABCDE的内角都相等,且∠ADE=∠DAE,∠BDC=∠DBC,则∠ADB=( )
A.18° B.36° C.72° D.108°
8.等腰三角形两边长分别为2和4,则这个等腰三角形的周长为( )
A.6 B.8 C.10 D.8或10
9.如图,在△ABC中,AB=AC,∠A=30°,取大于的长为半径,分别以点A、B为圆心,作弧相交于两点,过此两点的直线交AC边于点D(作图痕迹如图所示),连接BD,则∠DBC的度数为( )
A.30° B.45° C.60° D.75°
10.一个正多边形的外角与其相邻的内角的度数之比为2:7,那么这个多边形的边数为( )
A.8 B.9 C.10 D.12
二.填空题(共5小题,满分15分,每小题3分)
11.计算:20200+()﹣1= .
12.若关于x的分式方程无解,则a的值为 .
13.已知a+b=﹣5,ab=6,则a2+b2= .
14.如图,CE平分∠ACD,交AB于点E,若∠A=40°,∠B=30°,∠BDC=110°,则∠BEC的度数为 .
15.如图,在△ABC中,∠ACB=60°,点D在AB上,CD=14,∠BDC=60°,延长CB至点E,使CE=AC,过点E作EF⊥CD于点F,交AB于点G,若2DG=AD,则DF= .
(14题图) (15题图)
三.解答题(共8小题,满分75分)
16.(10分)(1)计算:(4x+1)(x﹣2)﹣(2x﹣3)2; (2)解方程:.
17.(8分)先化简再求值:(1),再从0,﹣1,2中选一个数作为a的值代入求值.
18.(9分)如图,DE⊥AB于点E,DF⊥AC于点F,BD=CD,BE=CF.
(1)求证:DE=DF;
(2)已知AC=20,BE=4,求AB的长.
19.(9分)如图,在平面直角坐标系中,△ABC顶点的坐标分别是A(﹣1,3),B(﹣5,1),C(﹣2,﹣2).
(1)画出△ABC关于y轴对称的△A′B′C′;
(2)直接写出A′,B′,C′三点的坐标;
(3)请在x轴上画点P,使得PA+PB最短(保留作图痕迹,不写画法).
20.(9分)材料:把多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.
例如:am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(a+b)(m+n).
(1)分解因式:ab+a+b+1;
(2)若a,b(a>b)都是正整数且满足ab﹣a﹣b﹣4=0,求a+b的值;
(3)若a,b为实数且满足ab﹣a﹣b﹣5=0,S=2a2+3ab+b2+5a﹣b,求S的最小值.
21.(9分)如图,AE⊥DB,CF⊥DB,垂足分别是点E,F,DE=BF,AB=CD.
求证:∠A=∠C.
22.(10分)受疫情影响,“84”消毒液需求量猛增,某商场用8000元购进一批“84”消毒液后,供不应求,商场用17600元购进第二批这种“84”消毒液,所购数量是第一批数量的2倍,但单价贵了1元.
(1)求该商场购进的第一批“84”消毒液的单价;
(2)商场销售这种“84”消毒液时,每瓶定价为13元,最后200瓶按9折销售,很快售完,在这两笔生意中商场共获利多少元?
23.(11分)如图,已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).
(1)如图1,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图3中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D A D B C B B
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、,不是最简分式,不符合题意;
B、,不是最简分式,不符合题意;
C、是最简分式,符合题意;
D、1,不是最简分式,不符合题意;
选:C.
2.解:(﹣2m4)3=(﹣2)3×(m4)3=﹣8m12,
选:D.
3.解:∵(a+b)2=a2+2ab+b2,选项A错误;
∵a2×a3=a5,选项B错误;
∵(a﹣b)(b﹣a)=﹣a2+2ab﹣b2,选项C错误;
∵(a2)3=a6,选项D正确;
选:D.
4.证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS).
选:D.
5.解:∵4x2+kx+9=(2x)2+kx+32,
∴kx=±2 2x 3,
解得:k=±12.
选:A.
6.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,BD平分∠ABC,
∴DE=CD,
∵AC=14,且AD:DC=4:3,
∴DC=146,
∴DE=CD=6,
即点D到AB的距离DE等于6,
选:D.
7.解:∵五边形ABCDE的内角都相等,
∴∠BAE=∠ABC=∠EDC=∠C=∠E=(5﹣2)×180°÷5=108°,
∴∠ADE=∠DAE=(180°﹣108°)÷2=36°,
∴∠DAB=∠BE﹣∠DAE=72°,
∠BDC=∠DBC=72°,
∴∠ADB=180°﹣∠DAB﹣∠DBA=36°.
选:B.
8.解:①2是腰长时,三角形的三边分别为2、2、4,
∵2+2=4,
∴不能组成三角形;
②2是底边时,三角形的三边分别为2、4、4,
能组成三角形,
周长=2+4+4=10,
综上所述,三角形的周长为10.
选:C.
9.解:由题意得,点D在线段AB的垂直平分线上,
∴AD=BD,
∴∠DBA=∠A=30°,
∵AB=AC,
∴,
∴∠DBC=∠ABC﹣∠DBA=45°,
选:B.
10.解:设正多边形的每个外角的度数为2x,与它相邻的内角的度数为7x,依题意有:
2x+7x=180°,
解得x=20°,
这个多边形的边数=360°÷40°=9.
选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:原式=1+3=4,
答案为:4.
12.解:,
3x+9+ax=4x﹣12,
(a﹣1)x=﹣21,
∵分式方程无解,
∴分两种情况:
当a﹣1=0时,a=1,
当(x+3)(x﹣3)=0时,x=±3,
把x=±3分别代入(a﹣1)x=﹣21中,
得a=8或﹣6,
综上所述:a的值为1或8或﹣6.
答案为:1或8或﹣6.
13.解:∵a+b=﹣5,
∴(a+b)2=25,
∴a2+2ab+b2=25.
∵ab=6,
∴a2+b2+12=25,
∴a2+b2=13.
答案为:13.
14.解:作射线AD,如图,
由三角形外角的性质得到:∠BDC=∠BDF+∠CDF=∠BAD+∠B+∠CAD+∠ACD=∠BAC+∠B+∠ACD,
又∵∠BAC=40°,∠B=30°,∠BDC=110°,
则∠ACD=∠BDC﹣∠BAC﹣∠B=110°﹣40°﹣30°=40°,
∵CE平分∠ACD,
∴,
∴∠BEC=∠BAC+∠ACE=40°+20°=60°,
即∠BEC=60°.
答案为:60°.
15.解:过点C作CH⊥AB于点H,如图所示:
设DF=x,
∵CD=14,
∴CF=CD﹣DF=14﹣x,
∵EF⊥CD,
在Rt△DFG中,∠BDC=60°,
∴∠DGF=30°,
∴DG=2DF=2x,
∵2DG=AD,
∴AD=2DG=4x,
∵CH⊥AB,
在Rt△CHD中,∠BDC=60°,
∴∠DCH=30°,
∴DHCD=7,
∴AH=AD+DH=4x+7,
∵∠BDC=∠A+∠ACD=60°,∠ACB=∠ACD+∠FCE=60°,
∴∠A=∠FCE,
又∵CH⊥AB,EF⊥CD,
∴∠AHC=∠CFE=90°,
在△ACH和△CFE中,
,
∴△ACH≌△CFE(AAS),
∴AH=CF,
∴4x+7=14﹣x,
解得:x.
答案为:.
三.解答题(共8小题,满分75分)
16.解:(1)原式=4x2﹣8x+x﹣2﹣(4x2﹣12x+9)
=4x2﹣8x+x﹣2﹣4x2+12x﹣9
=5x﹣11;
(2)去分母得:x(x+2)﹣x2+4=2,
解答:x=﹣1,
检验:把x=﹣1代入得:(x+2)(x﹣2)≠0,
∴分式方程的解为x=﹣1.
17.解:(1)
,
∵当a=﹣1或2时,原分式无意义,
∴a=0,
当a=0时,原式.
18.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中,BD=CD,BE=CF,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
(2)解:在Rt△BED和Rt△CFD中,AE=DF,AD=AD,
∴Rt△ADE≌Rt△ADF(HL),
∵△ADE≌△ADF,Rt△BED≌Rt△CFD,
∴AE=AF,CF=BE=4,
∵AC=20,
∴AE=AF=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.
19.(1)解:如图所示,△A′B′C′即为所求,
(2)解:由图知A′(1,3),B′(5,1),C′(2,﹣2);
(3)解:如图所示,点P即为所求.
20.解:(1)ab+a+b+1
=(ab+a)+(b+1)
=a(b+1)+(b+1)
=(a+1)(b+1);
(2)由题得ab﹣a﹣b+1=5,即(a﹣1)(b﹣1)=5,
∵a,b为正整数且a>b,
∴,即,
∴a+b=8;
(2)由题得ab=a+b+5,
S=2a2+3ab+b2+5a﹣b
=2a2+3a+3b+15+b2+5a﹣b
=2a2+8a+b2+2b+15
=2(a2+4a+4)+(b2+2b+1)+6
=2(a+2)2+(b+1)2+6,
∵(a+2)2≥0,(b+1)2≥0,
∴S≥6,(当且仅当a=﹣2,b=﹣1时取等号),
经验证:a=﹣2,b=﹣1满足ab﹣a﹣b﹣5=0,
综上,S的最小值为6.
21.证明:∵AE⊥DB,CF⊥DB,
∴∠AEB=∠CFD=90°,
∵DE=BF,
∴DF=BE,
在Rt△ABE和Rt△CDF中,
∴Rt△ABE≌Rt△CDF(HL),
∴∠A=∠C.
22.解:(1)设该商场购进的第一批“84”消毒液单价为x元/瓶,依题意得:2.
解得,x=10.
经检验,x=10是原方程的根.
所以该商场购进的第一批消毒液的单价为10元/瓶;
(2)共获利:(200)×13+200×13×0.9﹣(8000+17600)=5340(元).
在这两笔生意中商场共获得5340元.
23.解:(1)判断:EN与MF相等(或EN=MF),点F在直线NE上,
(2)成立.
延长EN交BC于点F,连接DF,
∵△ABC是等边三角形,
∴AB=AC=BC.
∵DMN为等边三角形,DM=DN,
又∵D,E,F是三边的中点,
∴EF=DF=BF,则BD=DF,
∵∠BDM+∠MDF=60°,∠FDN+∠MDF=60°,
∴∠BDM=∠FDN,
在△DBM和△DFN中,
,
∴△DBM≌△DFN(SAS),
∴BM=FN,∠DFN=∠FDB=60°,
∴NF∥BD,
∵E,F分别为边AC,BC的中点,
∴EF是△ABC的中位线,
∴EF∥BD,
∴F在直线NE上,
∵BF=EF,
∴MF=EN.
(3)如图③,MF与EN相等的结论仍然成立(或MF=NE成立).
连接DF、DE,
由(2)知DE=DF,∠NDE=∠FDM,DN=DM,
在△DNE和△DMF中,
∴△DNE≌△DMF(SAS),
∴MF=NE.
第12页(共12页)
