2025浙江高考物理一轮复习-“17~20解答”限时练13(含解析)
文档属性
| 名称 | 2025浙江高考物理一轮复习-“17~20解答”限时练13(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-02 12:42:27 | ||
图片预览


文档简介
2025浙江高考物理一轮复习-“17~20解答”限时练13
17.(8分)[2024·嘉兴模拟] 如图所示为一超重报警装置,其主体是水平地面上的导热性能良好的竖直薄壁密闭容器.容器高H=0.5 m、横截面积S=0.06 m2,底部是深h=0.1 m的预警区域,内有一厚度和质量均不计的活塞.活塞通过轻杆连接轻质平台,当活塞进入预警区域时,系统会发出超重预警.平台上未放重物时,内部封闭气柱长度L=0.4 m;平台上轻放质量为M的重物时,活塞最终恰好稳定在预警区域上边界.已知环境温度T0=27 ℃,大气压强p0=1.0×105 Pa,g取10 m/s2,不计摩擦阻力.
(1)求重物的质量M;
(2)求放上M至活塞最终稳定的过程中,密闭气体与外界交换的热量Q;
(3)若环境温度变为-3 ℃且外界大气压强不变,为保证放上M后活塞最终仍稳定在预警区域上边界,应充装与封闭气体同温同压的气体多少体积
18.(11分)[2024·台州一中模拟] 如图所示,某装置由水平直轨道AE、半径为R1的螺旋圆形轨道BCD、长 L1的水平传送带EF、长 L2的水平直轨道FG、半径为 R2的竖直圆轨道组成,两个圆形轨道与水平轨道分别相切于B(D)、G点.轨道A 处的水平弹射器能使质量为m1的小滑块获得8 J的初动能.G点上静止放置质量为m2的小滑块,两滑块若碰撞则粘在一起,且不计碰撞所需时间.已知 R1=0.2 m,L1=1 m,L2=1 m,R2=10 m,m1=1 kg,m2=9 kg,,滑块与传送带和FG段之间的动摩擦因数 μ=0.45,其余各段轨道均光滑且各处平滑连接,传送带以恒定速度顺时针转动,g取10 m/s2.求:
(1)滑块通过圆形轨道最高点C时轨道所受的压力;
(2)若要使两滑块碰撞损失的能量最大,传送带速度 v的最小值;
(3)要使两滑块能碰撞且最终停在直轨道FG上,则两滑块从碰撞到停止运动所需时间t与传送带速度v的关系.
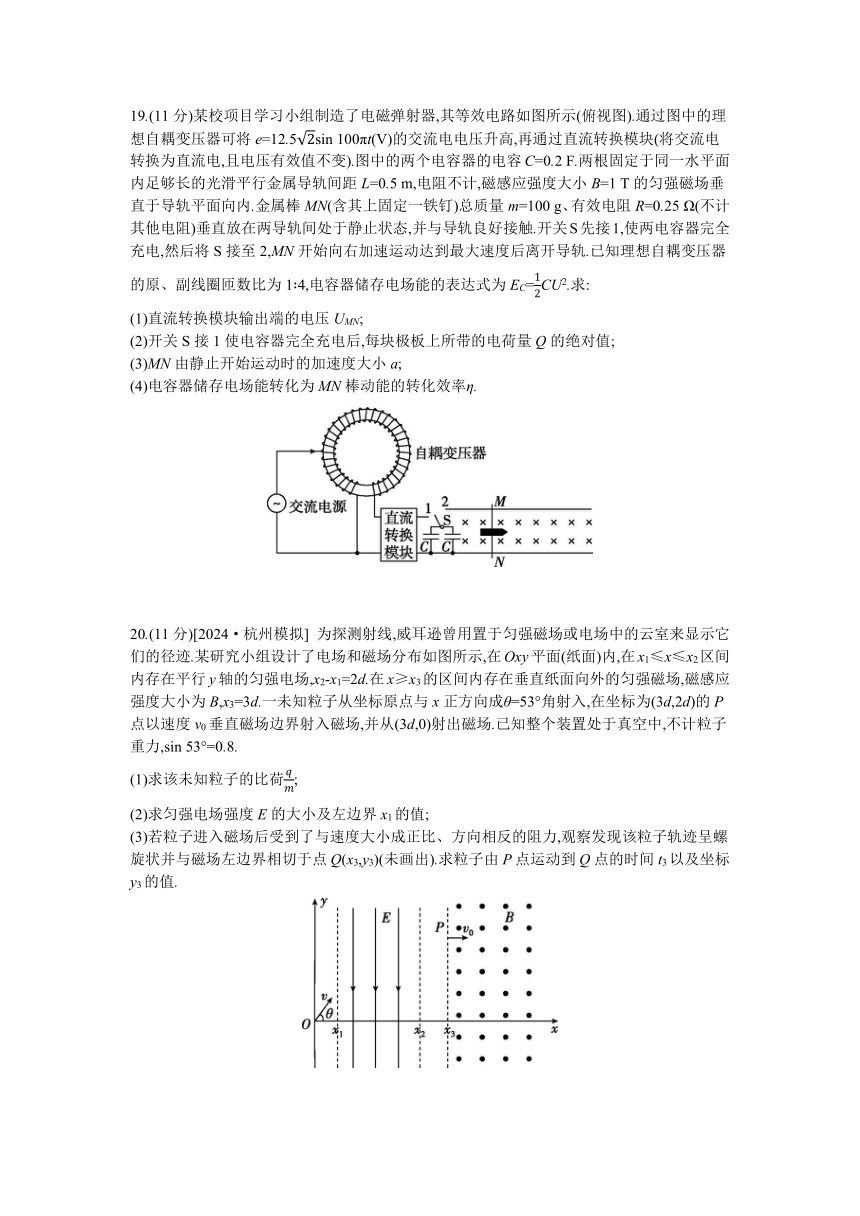
19.(11分)某校项目学习小组制造了电磁弹射器,其等效电路如图所示(俯视图).通过图中的理想自耦变压器可将e=12.5sin 100πt(V)的交流电电压升高,再通过直流转换模块(将交流电转换为直流电,且电压有效值不变).图中的两个电容器的电容C=0.2 F.两根固定于同一水平面内足够长的光滑平行金属导轨间距L=0.5 m,电阻不计,磁感应强度大小B=1 T的匀强磁场垂直于导轨平面向内.金属棒MN(含其上固定一铁钉)总质量m=100 g、有效电阻R=0.25 Ω(不计其他电阻)垂直放在两导轨间处于静止状态,并与导轨良好接触.开关S先接1,使两电容器完全充电,然后将S接至2,MN开始向右加速运动达到最大速度后离开导轨.已知理想自耦变压器的原、副线圈匝数比为1∶4,电容器储存电场能的表达式为EC=CU2.求:
(1)直流转换模块输出端的电压UMN;
(2)开关S接1使电容器完全充电后,每块极板上所带的电荷量Q的绝对值;
(3)MN由静止开始运动时的加速度大小a;
(4)电容器储存电场能转化为MN棒动能的转化效率η.
20.(11分)[2024·杭州模拟] 为探测射线,威耳逊曾用置于匀强磁场或电场中的云室来显示它们的径迹.某研究小组设计了电场和磁场分布如图所示,在Oxy平面(纸面)内,在x1≤x≤x2区间内存在平行y轴的匀强电场,x2-x1=2d.在x≥x3的区间内存在垂直纸面向外的匀强磁场,磁感应强度大小为B,x3=3d.一未知粒子从坐标原点与x正方向成θ=53°角射入,在坐标为(3d,2d)的P点以速度v0垂直磁场边界射入磁场,并从(3d,0)射出磁场.已知整个装置处于真空中,不计粒子重力,sin 53°=0.8.
(1)求该未知粒子的比荷;
(2)求匀强电场强度E的大小及左边界x1的值;
(3)若粒子进入磁场后受到了与速度大小成正比、方向相反的阻力,观察发现该粒子轨迹呈螺旋状并与磁场左边界相切于点Q(x3,y3)(未画出).求粒子由P点运动到Q点的时间t3以及坐标y3的值.
参考答案与详细解析
17.(1)1.8×103 kg (2)气体对外界放出的热量为7.2×103 J (3)2.4×10-3 m3
[解析] (1)最终稳定时,封闭气体温度不变,则
p0LS=p1hS
可得p1=4p0 (1分)
又因为p1=p0+ (1分)
代入相关已知数据求得M=1.8×103 kg(1分)
(2)设外界大气压力和重物对封闭气体做功为W,则
W=(Mg+p0S)(L-h) (1分)
代入数据求得W=7.2×103 J(1分)
在(1)问的情况下,封闭气体内能不变(ΔU=0),根据热力学第一定律ΔU=Q+W可得,气体对外界放出的热量为
Q=7.2×103 J(1分)
(3)外界大气压强不变,所以环境温度变化时,满足
=
即=
解得V1=0.9V0 (1分)
所以应充装同温同压的气体体积为
ΔV=V0-0.9V0=0.1LS=2.4×10-3 m3 (1分)
18.(1)30 N,方向竖直向上
(2)5 m/s (3)见解析
[解析] (1)滑块从B到C由动能定理有-m1g·2R1=m1-Ek0 (1分)
在C点,m1g+FN=m1 (1分)
解得FN=30 N
由牛顿第三定律知轨道所受压力大小为30 N,方向竖直向上 (1分)
(2)质量为m1的滑块在传送带上一直匀加速运动时, 出传送带时的速度最大,则两滑块碰撞后损失的能量最大
从弹出滑块到F处,由动能定理μm1gL1=m1v2-Ek0 (1分)
解得v=5 m/s
所以传送带速度的最小值为 5 m/s(1分)
(3)①当传送带速度v≥5 m/s 时,质量为m1的滑块出传送带时vF=5 m/s
质量为m1的滑块从F到G过程, 由动能定理-μm1gL2=m1-m1
解得vG=4 m/s(1分)
两滑块碰撞过程动量守恒m1vG=(m1+m2)v共
解得v共=0.4 m/s(1分)
两滑块碰后能上升的最大高度为 h, 由动能定理(m1+m2)=(m1+m2)gh
解得 h=0.008 m R2=10 m
故两滑块在半径为R2的圆内运动可看为单摆模型,周期 T=2π=2π s(1分)
时间 t1==π s
两滑块返回G 点后到停止运动有=2μgs
解得s= m对应时间 t2== s
t=t1+t2= s(1分)
②出F后恰好运动到G点时有=2μgL2,此时vF=3 m/s(1分)
当传送带速度满足3 m/s解得t= s(1分)
19.(1)50 V (2)10 C (3)1.0×103 m/s2 (4)33%
[解析] (1)交流电电压的有效值为
U1= V=12.5 V(1分)
根据变压器的电压匝数关系有
= (1分)
由题意可知直流转换模块输出端的电压
UMN=U2
解得UMN=50 V(1分)
(2)根据电容的定义式有
C=
解得Q=10 C(1分)
(3)MN由静止开始运动时的电流
I= (1分)
此时对金属棒进行分析,根据牛顿第二定律有
BIL=ma
解得a=1.0×103 m/s2 (1分)
(4)MN开始向右加速运动达到最大速度时,金属棒切割磁感线产生的感应电动势与此时电容器极板电压相等,则有
U=BLvmax (1分)
根据动量定理有
BLt=mvmax-0 (1分)
该过程通过金属棒的电荷量
q=t=2C (1分)
结合上述解得
vmax=50 m/s
考虑最后电容器还有电场能储存,则有
η= (1分)
结合上述解得
η=≈33%(1分)
20.(1) (2)
(3) d
[解析] (1)粒子在磁场中,由洛伦兹力提供向心力可得qv0B=m (1分)
又R=d
联立解得粒子的比荷为= (1分)
(2)粒子的轨迹如图所示
粒子在电场中可逆向看成做类平抛运动,则有
2d=v0t1
vy=v0tan 53°=at1
a=
联立解得匀强电场强度大小为E= (2分)
由几何关系可得x1tan 53°+a=2d
解得x1= (2分)
(3)若粒子进入磁场后受到了与速度大小成正比、方向相反的阻力,粒子在磁场的运动轨迹如图所示
由qvB=mωv可得ω= (1分)
即角速度为一定值,又可知粒子与磁场左边界相切时转过的弧度为π
则有t3== (1分)
取一小段时间Δt,在x方向上应用对粒子动量定理(如图),有
-kvsin α·Δt-qvBcos α·Δt=mΔvx (1分)
则有qBΔy=-mv0 (1分)
结合=
可得Δy=-=-d
故有y3=2d-d=d (1分)
17.(8分)[2024·嘉兴模拟] 如图所示为一超重报警装置,其主体是水平地面上的导热性能良好的竖直薄壁密闭容器.容器高H=0.5 m、横截面积S=0.06 m2,底部是深h=0.1 m的预警区域,内有一厚度和质量均不计的活塞.活塞通过轻杆连接轻质平台,当活塞进入预警区域时,系统会发出超重预警.平台上未放重物时,内部封闭气柱长度L=0.4 m;平台上轻放质量为M的重物时,活塞最终恰好稳定在预警区域上边界.已知环境温度T0=27 ℃,大气压强p0=1.0×105 Pa,g取10 m/s2,不计摩擦阻力.
(1)求重物的质量M;
(2)求放上M至活塞最终稳定的过程中,密闭气体与外界交换的热量Q;
(3)若环境温度变为-3 ℃且外界大气压强不变,为保证放上M后活塞最终仍稳定在预警区域上边界,应充装与封闭气体同温同压的气体多少体积
18.(11分)[2024·台州一中模拟] 如图所示,某装置由水平直轨道AE、半径为R1的螺旋圆形轨道BCD、长 L1的水平传送带EF、长 L2的水平直轨道FG、半径为 R2的竖直圆轨道组成,两个圆形轨道与水平轨道分别相切于B(D)、G点.轨道A 处的水平弹射器能使质量为m1的小滑块获得8 J的初动能.G点上静止放置质量为m2的小滑块,两滑块若碰撞则粘在一起,且不计碰撞所需时间.已知 R1=0.2 m,L1=1 m,L2=1 m,R2=10 m,m1=1 kg,m2=9 kg,,滑块与传送带和FG段之间的动摩擦因数 μ=0.45,其余各段轨道均光滑且各处平滑连接,传送带以恒定速度顺时针转动,g取10 m/s2.求:
(1)滑块通过圆形轨道最高点C时轨道所受的压力;
(2)若要使两滑块碰撞损失的能量最大,传送带速度 v的最小值;
(3)要使两滑块能碰撞且最终停在直轨道FG上,则两滑块从碰撞到停止运动所需时间t与传送带速度v的关系.
19.(11分)某校项目学习小组制造了电磁弹射器,其等效电路如图所示(俯视图).通过图中的理想自耦变压器可将e=12.5sin 100πt(V)的交流电电压升高,再通过直流转换模块(将交流电转换为直流电,且电压有效值不变).图中的两个电容器的电容C=0.2 F.两根固定于同一水平面内足够长的光滑平行金属导轨间距L=0.5 m,电阻不计,磁感应强度大小B=1 T的匀强磁场垂直于导轨平面向内.金属棒MN(含其上固定一铁钉)总质量m=100 g、有效电阻R=0.25 Ω(不计其他电阻)垂直放在两导轨间处于静止状态,并与导轨良好接触.开关S先接1,使两电容器完全充电,然后将S接至2,MN开始向右加速运动达到最大速度后离开导轨.已知理想自耦变压器的原、副线圈匝数比为1∶4,电容器储存电场能的表达式为EC=CU2.求:
(1)直流转换模块输出端的电压UMN;
(2)开关S接1使电容器完全充电后,每块极板上所带的电荷量Q的绝对值;
(3)MN由静止开始运动时的加速度大小a;
(4)电容器储存电场能转化为MN棒动能的转化效率η.
20.(11分)[2024·杭州模拟] 为探测射线,威耳逊曾用置于匀强磁场或电场中的云室来显示它们的径迹.某研究小组设计了电场和磁场分布如图所示,在Oxy平面(纸面)内,在x1≤x≤x2区间内存在平行y轴的匀强电场,x2-x1=2d.在x≥x3的区间内存在垂直纸面向外的匀强磁场,磁感应强度大小为B,x3=3d.一未知粒子从坐标原点与x正方向成θ=53°角射入,在坐标为(3d,2d)的P点以速度v0垂直磁场边界射入磁场,并从(3d,0)射出磁场.已知整个装置处于真空中,不计粒子重力,sin 53°=0.8.
(1)求该未知粒子的比荷;
(2)求匀强电场强度E的大小及左边界x1的值;
(3)若粒子进入磁场后受到了与速度大小成正比、方向相反的阻力,观察发现该粒子轨迹呈螺旋状并与磁场左边界相切于点Q(x3,y3)(未画出).求粒子由P点运动到Q点的时间t3以及坐标y3的值.
参考答案与详细解析
17.(1)1.8×103 kg (2)气体对外界放出的热量为7.2×103 J (3)2.4×10-3 m3
[解析] (1)最终稳定时,封闭气体温度不变,则
p0LS=p1hS
可得p1=4p0 (1分)
又因为p1=p0+ (1分)
代入相关已知数据求得M=1.8×103 kg(1分)
(2)设外界大气压力和重物对封闭气体做功为W,则
W=(Mg+p0S)(L-h) (1分)
代入数据求得W=7.2×103 J(1分)
在(1)问的情况下,封闭气体内能不变(ΔU=0),根据热力学第一定律ΔU=Q+W可得,气体对外界放出的热量为
Q=7.2×103 J(1分)
(3)外界大气压强不变,所以环境温度变化时,满足
=
即=
解得V1=0.9V0 (1分)
所以应充装同温同压的气体体积为
ΔV=V0-0.9V0=0.1LS=2.4×10-3 m3 (1分)
18.(1)30 N,方向竖直向上
(2)5 m/s (3)见解析
[解析] (1)滑块从B到C由动能定理有-m1g·2R1=m1-Ek0 (1分)
在C点,m1g+FN=m1 (1分)
解得FN=30 N
由牛顿第三定律知轨道所受压力大小为30 N,方向竖直向上 (1分)
(2)质量为m1的滑块在传送带上一直匀加速运动时, 出传送带时的速度最大,则两滑块碰撞后损失的能量最大
从弹出滑块到F处,由动能定理μm1gL1=m1v2-Ek0 (1分)
解得v=5 m/s
所以传送带速度的最小值为 5 m/s(1分)
(3)①当传送带速度v≥5 m/s 时,质量为m1的滑块出传送带时vF=5 m/s
质量为m1的滑块从F到G过程, 由动能定理-μm1gL2=m1-m1
解得vG=4 m/s(1分)
两滑块碰撞过程动量守恒m1vG=(m1+m2)v共
解得v共=0.4 m/s(1分)
两滑块碰后能上升的最大高度为 h, 由动能定理(m1+m2)=(m1+m2)gh
解得 h=0.008 m R2=10 m
故两滑块在半径为R2的圆内运动可看为单摆模型,周期 T=2π=2π s(1分)
时间 t1==π s
两滑块返回G 点后到停止运动有=2μgs
解得s= m
t=t1+t2= s(1分)
②出F后恰好运动到G点时有=2μgL2,此时vF=3 m/s(1分)
当传送带速度满足3 m/s
19.(1)50 V (2)10 C (3)1.0×103 m/s2 (4)33%
[解析] (1)交流电电压的有效值为
U1= V=12.5 V(1分)
根据变压器的电压匝数关系有
= (1分)
由题意可知直流转换模块输出端的电压
UMN=U2
解得UMN=50 V(1分)
(2)根据电容的定义式有
C=
解得Q=10 C(1分)
(3)MN由静止开始运动时的电流
I= (1分)
此时对金属棒进行分析,根据牛顿第二定律有
BIL=ma
解得a=1.0×103 m/s2 (1分)
(4)MN开始向右加速运动达到最大速度时,金属棒切割磁感线产生的感应电动势与此时电容器极板电压相等,则有
U=BLvmax (1分)
根据动量定理有
BLt=mvmax-0 (1分)
该过程通过金属棒的电荷量
q=t=2C (1分)
结合上述解得
vmax=50 m/s
考虑最后电容器还有电场能储存,则有
η= (1分)
结合上述解得
η=≈33%(1分)
20.(1) (2)
(3) d
[解析] (1)粒子在磁场中,由洛伦兹力提供向心力可得qv0B=m (1分)
又R=d
联立解得粒子的比荷为= (1分)
(2)粒子的轨迹如图所示
粒子在电场中可逆向看成做类平抛运动,则有
2d=v0t1
vy=v0tan 53°=at1
a=
联立解得匀强电场强度大小为E= (2分)
由几何关系可得x1tan 53°+a=2d
解得x1= (2分)
(3)若粒子进入磁场后受到了与速度大小成正比、方向相反的阻力,粒子在磁场的运动轨迹如图所示
由qvB=mωv可得ω= (1分)
即角速度为一定值,又可知粒子与磁场左边界相切时转过的弧度为π
则有t3== (1分)
取一小段时间Δt,在x方向上应用对粒子动量定理(如图),有
-kvsin α·Δt-qvBcos α·Δt=mΔvx (1分)
则有qBΔy=-mv0 (1分)
结合=
可得Δy=-=-d
故有y3=2d-d=d (1分)
同课章节目录
