17.1勾股定理 教学设计(表格式) 人教版数学八年级下册
文档属性
| 名称 | 17.1勾股定理 教学设计(表格式) 人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 367.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 00:00:00 | ||
图片预览

文档简介
《17.1勾股定理》教学设计
课题 17.1勾股定理 课型 新授课
教 学 目 标 1.掌握勾股定理的内容和证明方法。 2.会用勾股定理进行简单的计算。
3.经历探究勾股定理的过程,发展合情推理能力,体会数形结合思想,学会与人合作并能与他人交流思维的过程和探究结果,体会数学思维的严谨性,并尝试学生自己讲题,提高逻辑思维和语言表达能力。
4.通过我国古代对勾股定理研究方面缩取得的成就,感受数学的文化,激发学习激情和爱国热情,培养在实际生活中发现问题总结规律的意识和能力;养成数学说理的习惯。
教材 分析 教学方法 和手段 采用教师的启发引导和学生的自主探究、动手操作、小组交流讨论相结合的教学方法,利用信息技术,多媒体等手段教学。
重点 掌握勾股定理的证明,会用勾股定理进行简单的计算。
难点 勾股定理的证明。
教具学具 多媒体设备,不同的三角形卡纸若干。
授课步骤 教师活动 学生活动 设计意图
知 识 回 顾 一、课堂活动导入:关于数的平方和平方根的计算的PK小游戏。 两名学生PK 利用课堂活动的PK小游戏快速吸引学生注意力,使学生以轻松愉快的心情进入本节课的学习。
情 境 导 入 二、情境引入 1.北京举行的国际数学家大会的会徽。 2.展示古代对直角三角形的认识。 3.相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系. 图中的三个正方形的面积有什么关系?等腰直角三角形的三边有什么关系? 学生思考交流说出自己的发现并回答:以等腰直角三角形为边长的两个小正方形的面积之和等于以斜边为边长的大正方形的面积。 动画演示数量关系 追问:对于一般的直角三角形是不是也有上述性质呢? 观察,思考,回答教师所提出的各个问题 用情境导入,会徽设疑引出本节课题。为新知识作铺垫。明确本节课所要学习的主要内容
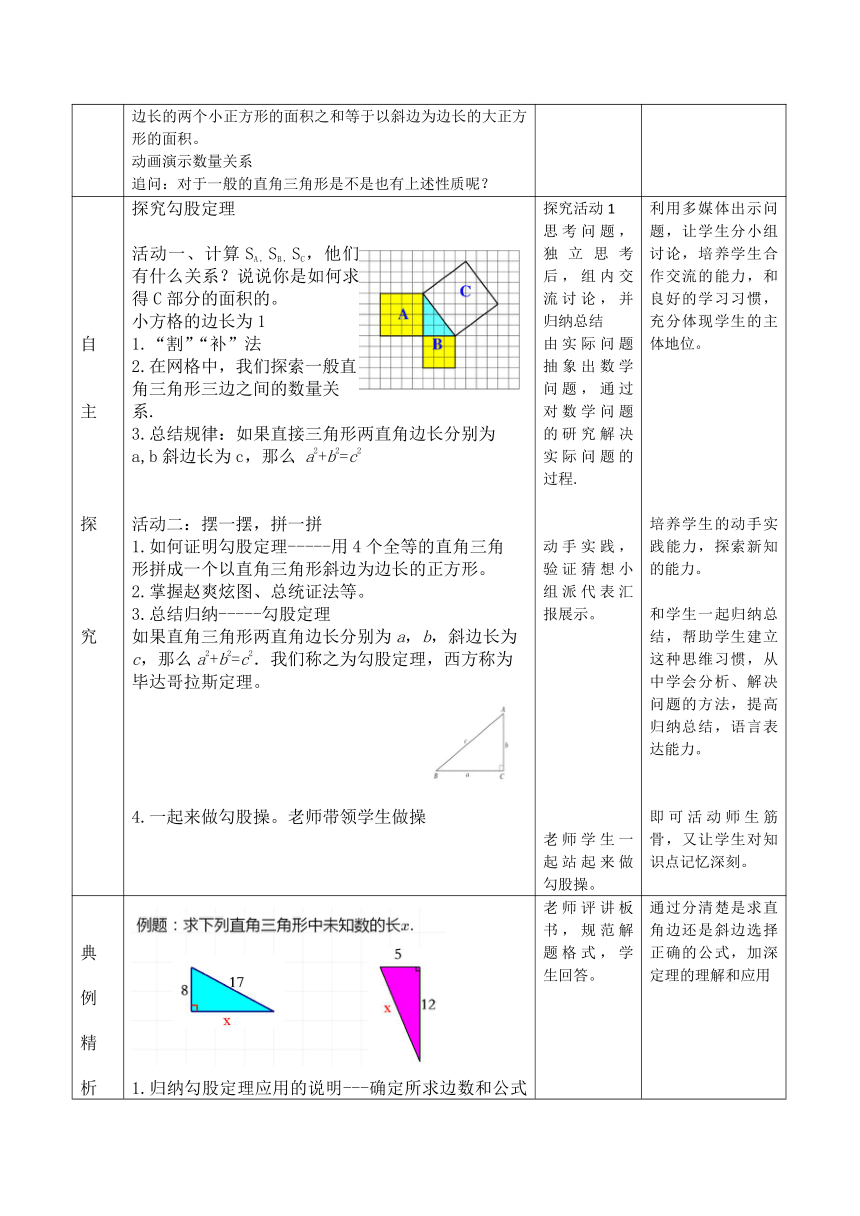
自 主 探 究 探究勾股定理 活动一、计算SA,SB,SC,他们有什么关系?说说你是如何求得C部分的面积的。 小方格的边长为1 1.“割”“补”法 2.在网格中,我们探索一般直角三角形三边之间的数量关系. 3.总结规律:如果直接三角形两直角边长分别为a,b斜边长为c,那么 a2+b2=c2 活动二:摆一摆,拼一拼 1.如何证明勾股定理-----用4个全等的直角三角形拼成一个以直角三角形斜边为边长的正方形。 2.掌握赵爽炫图、总统证法等。 3.总结归纳-----勾股定理 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.我们称之为勾股定理,西方称为毕达哥拉斯定理。 4.一起来做勾股操。老师带领学生做操 探究活动1 思考问题,独立思考后,组内交流讨论,并归纳总结 由实际问题抽象出数学问题,通过对数学问题的研究解决实际问题的过程. 动手实践,验证猜想小组派代表汇报展示。 老师学生一起站起来做勾股操。 利用多媒体出示问题,让学生分小组讨论,培养学生合作交流的能力,和良好的学习习惯,充分体现学生的主体地位。 培养学生的动手实践能力,探索新知的能力。 和学生一起归纳总结,帮助学生建立这种思维习惯,从中学会分析、解决问题的方法,提高 归纳总结,语言表达能力。 即可活动师生筋骨,又让学生对知识点记忆深刻。
典 例 精 析 1.归纳勾股定理应用的说明---确定所求边数和公式的灵活应用。 老师评讲板书,规范解题格式,学生回答。 通过分清楚是求直角边还是斜边选择正确的公式,加深定理的理解和应用
尝 试 应 用 课堂练习 练习3 课本本课时练习3 一起欣赏勾股树 独立完成 交流比对 学生展示讲解 认真观看 通过练习加深学生对本节课知识的理解,也能更好的让老师对学生的掌握情况有更好的了解,巩固所学知识。 提高学生的逻辑思维能力和语言表达能力。 感受数学的美和魅力。
课 堂 小 结 我爱分享 本节课你有哪些收获要跟大家分享? 你认为本节还有哪些需要注意的地方? 分享所得和提出疑问,完成本节课小结、反思,梳理知识,互相取长补短,掌握解题方法 再一次突出本节课的重点,让学生体会与人分享的快乐
知 识 拓 展 学无止境,课堂延伸 1.腊纪念邮票 2.与外星人的沟通标志(华罗庚) 3.高斯的故事 认真听讲, 并交流发言感想 进一步培养学生良好的思维习惯,增强学生的求知欲。
达 标 检 测 1.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( ) A.8 B.9 C.10 D.11 2. 图中的四边形均为正方形,三角形为直角三角形,最大的正方形的边长为7 cm,则图中A,B两个正方形的面积之和为( ) A.28 cm2 B.42 cm2 C.49 cm2 D.63 cm2 3.如图,在△ABC中,AB=5,BC=6,BC边上的中线AD=4,那么AC的长是( ) A.5 B.6 C D.2 4.在Rt△ABC中,∠C=90°, (1)若a=8,b=15,则c= ; (2)若a=15,c=25,则b= ; (3)若c=41,b=40,则a= ; (4)若a∶b=3∶4,c=10,则SRt△ABC= . 5.一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为 . 6.一个直角三角形的两边长分别为3 cm和4 cm,则第三边的长为 . 7.已知,如图,在△ABC中,AB=BC=CA=2 cm,AD是边BC上的高. 求(1)AD的长;(2)△ABC的面积. 作业布置: 独立思考 自主完成 交流比对 通过检测加深学生对本节课知识的理解,也能更好的让老师对学生的掌握情况有更好的了解。
板 书 设 计
课题 17.1勾股定理 课型 新授课
教 学 目 标 1.掌握勾股定理的内容和证明方法。 2.会用勾股定理进行简单的计算。
3.经历探究勾股定理的过程,发展合情推理能力,体会数形结合思想,学会与人合作并能与他人交流思维的过程和探究结果,体会数学思维的严谨性,并尝试学生自己讲题,提高逻辑思维和语言表达能力。
4.通过我国古代对勾股定理研究方面缩取得的成就,感受数学的文化,激发学习激情和爱国热情,培养在实际生活中发现问题总结规律的意识和能力;养成数学说理的习惯。
教材 分析 教学方法 和手段 采用教师的启发引导和学生的自主探究、动手操作、小组交流讨论相结合的教学方法,利用信息技术,多媒体等手段教学。
重点 掌握勾股定理的证明,会用勾股定理进行简单的计算。
难点 勾股定理的证明。
教具学具 多媒体设备,不同的三角形卡纸若干。
授课步骤 教师活动 学生活动 设计意图
知 识 回 顾 一、课堂活动导入:关于数的平方和平方根的计算的PK小游戏。 两名学生PK 利用课堂活动的PK小游戏快速吸引学生注意力,使学生以轻松愉快的心情进入本节课的学习。
情 境 导 入 二、情境引入 1.北京举行的国际数学家大会的会徽。 2.展示古代对直角三角形的认识。 3.相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系. 图中的三个正方形的面积有什么关系?等腰直角三角形的三边有什么关系? 学生思考交流说出自己的发现并回答:以等腰直角三角形为边长的两个小正方形的面积之和等于以斜边为边长的大正方形的面积。 动画演示数量关系 追问:对于一般的直角三角形是不是也有上述性质呢? 观察,思考,回答教师所提出的各个问题 用情境导入,会徽设疑引出本节课题。为新知识作铺垫。明确本节课所要学习的主要内容
自 主 探 究 探究勾股定理 活动一、计算SA,SB,SC,他们有什么关系?说说你是如何求得C部分的面积的。 小方格的边长为1 1.“割”“补”法 2.在网格中,我们探索一般直角三角形三边之间的数量关系. 3.总结规律:如果直接三角形两直角边长分别为a,b斜边长为c,那么 a2+b2=c2 活动二:摆一摆,拼一拼 1.如何证明勾股定理-----用4个全等的直角三角形拼成一个以直角三角形斜边为边长的正方形。 2.掌握赵爽炫图、总统证法等。 3.总结归纳-----勾股定理 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.我们称之为勾股定理,西方称为毕达哥拉斯定理。 4.一起来做勾股操。老师带领学生做操 探究活动1 思考问题,独立思考后,组内交流讨论,并归纳总结 由实际问题抽象出数学问题,通过对数学问题的研究解决实际问题的过程. 动手实践,验证猜想小组派代表汇报展示。 老师学生一起站起来做勾股操。 利用多媒体出示问题,让学生分小组讨论,培养学生合作交流的能力,和良好的学习习惯,充分体现学生的主体地位。 培养学生的动手实践能力,探索新知的能力。 和学生一起归纳总结,帮助学生建立这种思维习惯,从中学会分析、解决问题的方法,提高 归纳总结,语言表达能力。 即可活动师生筋骨,又让学生对知识点记忆深刻。
典 例 精 析 1.归纳勾股定理应用的说明---确定所求边数和公式的灵活应用。 老师评讲板书,规范解题格式,学生回答。 通过分清楚是求直角边还是斜边选择正确的公式,加深定理的理解和应用
尝 试 应 用 课堂练习 练习3 课本本课时练习3 一起欣赏勾股树 独立完成 交流比对 学生展示讲解 认真观看 通过练习加深学生对本节课知识的理解,也能更好的让老师对学生的掌握情况有更好的了解,巩固所学知识。 提高学生的逻辑思维能力和语言表达能力。 感受数学的美和魅力。
课 堂 小 结 我爱分享 本节课你有哪些收获要跟大家分享? 你认为本节还有哪些需要注意的地方? 分享所得和提出疑问,完成本节课小结、反思,梳理知识,互相取长补短,掌握解题方法 再一次突出本节课的重点,让学生体会与人分享的快乐
知 识 拓 展 学无止境,课堂延伸 1.腊纪念邮票 2.与外星人的沟通标志(华罗庚) 3.高斯的故事 认真听讲, 并交流发言感想 进一步培养学生良好的思维习惯,增强学生的求知欲。
达 标 检 测 1.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( ) A.8 B.9 C.10 D.11 2. 图中的四边形均为正方形,三角形为直角三角形,最大的正方形的边长为7 cm,则图中A,B两个正方形的面积之和为( ) A.28 cm2 B.42 cm2 C.49 cm2 D.63 cm2 3.如图,在△ABC中,AB=5,BC=6,BC边上的中线AD=4,那么AC的长是( ) A.5 B.6 C D.2 4.在Rt△ABC中,∠C=90°, (1)若a=8,b=15,则c= ; (2)若a=15,c=25,则b= ; (3)若c=41,b=40,则a= ; (4)若a∶b=3∶4,c=10,则SRt△ABC= . 5.一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为 . 6.一个直角三角形的两边长分别为3 cm和4 cm,则第三边的长为 . 7.已知,如图,在△ABC中,AB=BC=CA=2 cm,AD是边BC上的高. 求(1)AD的长;(2)△ABC的面积. 作业布置: 独立思考 自主完成 交流比对 通过检测加深学生对本节课知识的理解,也能更好的让老师对学生的掌握情况有更好的了解。
板 书 设 计
