7.1相交线综合检测题(基础)(含答案)
文档属性
| 名称 | 7.1相交线综合检测题(基础)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 477.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 18:47:18 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
7.1相交线综合检测题(基础)
一、单选题
1.如图,直线AB和射线OC相交于点O,∠AOC=100°,则∠BOC等于( )
A.100° B.80° C.50° D.110°
2.如图,在点A处,有一个牧童在放牛,牛吃饱后要到河边饮水,牧童把牛牵到河边,沿的路径走才能使所走的路程最少,其依据是( )
A.经过一点有无数条直线 B.垂线段最短
C.两点之间,线段最短 D.两点确定一条直线
3.如图所示, 和 是对顶角的是( )
A. B.
C. D.
4.点A为直线BC外一点,AC⊥BC于点C,AC=6.点Р是直线BC上的动点,则线段AP长可能是( )
A.1 B.3 C.5 D.7
5.如图,直线c、b被直线a所截,则∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
6.如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°
7.如图,直线AB、CD相交于点O,若∠1+∠2=100°,则∠BOC等于( )
A.130° B.140° C.150° D.160°
8.两直线被第三条直线所截,∠1与∠2是同旁内角,且∠1=30° ,则∠2的度数为( )
A.150° B.30°
C.30° 或150° D.无法确定
9.如图,下列说法中,错误的是( )
A.∠4与∠B是同位角 B.∠B与∠C是同旁内角
C.∠2与∠C是同位角 D.∠1与∠3是内错角
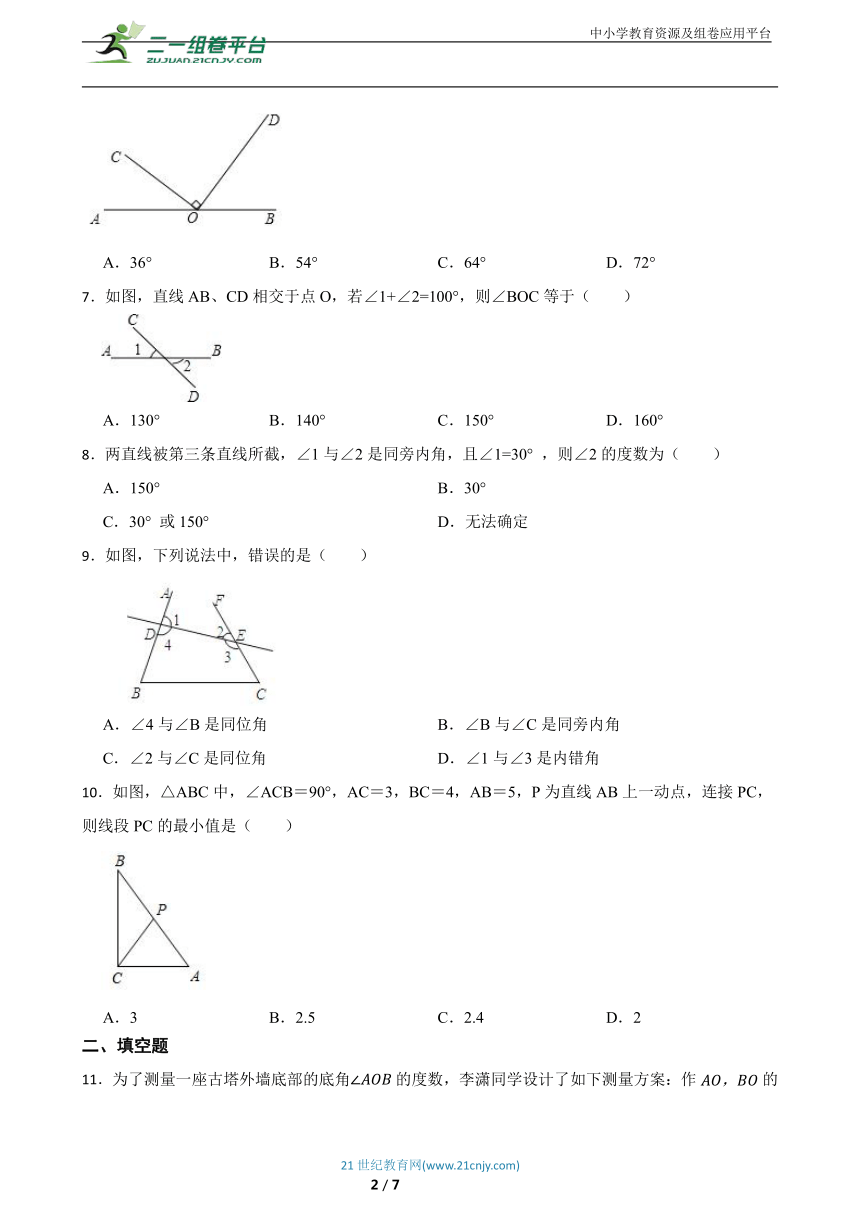
10.如图,△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,P为直线AB上一动点,连接PC,则线段PC的最小值是( )
A.3 B.2.5 C.2.4 D.2
二、填空题
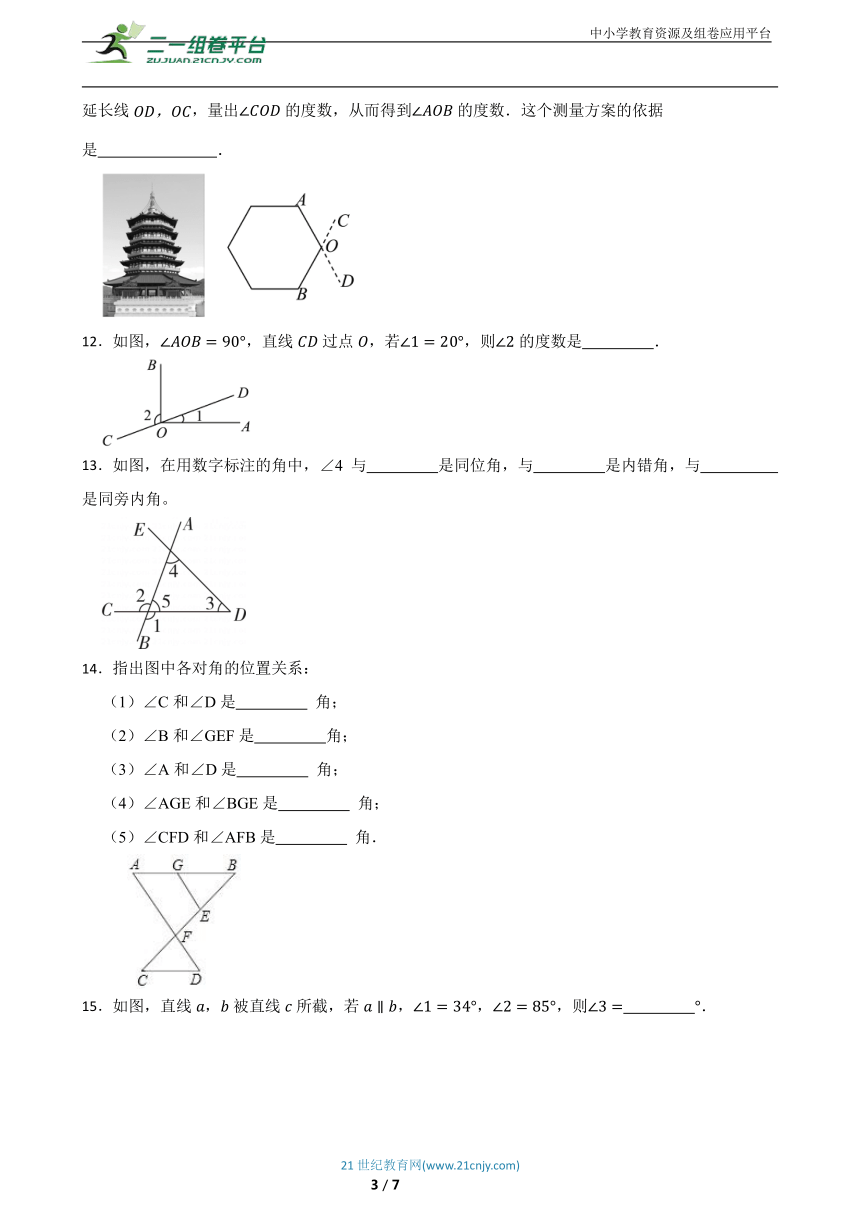
11.为了测量一座古塔外墙底部的底角的度数,李潇同学设计了如下测量方案:作的延长线,量出的度数,从而得到的度数.这个测量方案的依据是 .
12.如图,,直线过点,若,则的度数是 .
13.如图,在用数字标注的角中,∠4 与 是同位角,与 是内错角,与 是同旁内角。
14.指出图中各对角的位置关系:
(1)∠C和∠D是 角;
(2)∠B和∠GEF是 角;
(3)∠A和∠D是 角;
(4)∠AGE和∠BGE是 角;
(5)∠CFD和∠AFB是 角.
15.如图,直线,被直线所截,若,,,则 .
16.n条水平直线与倾斜直线a相交可得 条线段, 对同位角, 对内错角, 对同旁内角.
三、计算题
17.如图所示,已知,,计算的大小.
18.如图,O为直线AB上一点,OC⊥AB,并且∠AOD=130°.求∠COD的度数.
四、解答题
19.如图,直线AB,CD相交于点O,OM⊥AB,ON⊥CD.
(1)写出图中所有与∠AOC互余的角.
(2)当∠MON=120°时,求∠BOD 的度数.
20.找出图中所有的同位角、内错角和同旁内角。
21.如图,,OB是的平分线,C、O,D在同一条直线上.若,求的度数.
22.如图,直线AB,CD相交于点O,OC平分∠BOE,∠AOE=2∠FOD.
(1)若∠FOD=21°,求∠AOD的度数;
(2)猜想OE与OF的位置关系,并说明理由.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】D
9.【答案】A
10.【答案】C
11.【答案】对顶角相等
12.【答案】
13.【答案】∠1;∠2;∠3 和∠5
14.【答案】同旁内;同位;内错;邻补;对顶
15.【答案】
16.【答案】;2n(n﹣1);n(n﹣1);n(n﹣1)
17.【答案】
18.【答案】解:∵∠AOD=130°,
∴∠BOD=180°-∠AOD-80°-130°=50°.
∵OC⊥AB,
∴∠BOC=90°.
∴∠COD=∠BOD+∠BOC=50°+90°=140°.
19.【答案】(1)解:∠COM,∠AON
(2)解:60°
20.【答案】解:同位角:∠A与∠EDC,∠C 与∠ABF;
内错角:∠EDC与∠C,∠A与∠ABF;
同旁内角:∠A 与∠ABC,∠A 与∠ADC,∠C 与∠ABC,∠C与∠ADC
21.【答案】解:因为OB是的平分线,且,所以.
又因为,所以,
所以.
22.【答案】(1)解:∵∠FOD=21°,∠AOE=2∠FOD,∴∠AOE=42°,∴∠BOE=180°-∠AOE=180°-42°=138°.
∵OC平分∠BOE,∴∠BOC=-∠BOE=-×138°=69°,∴∠AOD=∠BOC=69°;
(2)解:猜想OE⊥OF,理由如下:
设∠DOF=x,则∠AOE=2x.
∴∠BOE=180°-2x.
∵OC平分∠BOE,
∴.
∴∠AOD=∠BOC=90°-x.
∴∠AOF=∠AOD-∠DOF=90°-2x.
∴∠EOF=∠AOE+∠AOF=2x+90°-2x=90°.
∴OE⊥OF.
21世纪教育网(www.21cnjy.com)
1 / 7
7.1相交线综合检测题(基础)
一、单选题
1.如图,直线AB和射线OC相交于点O,∠AOC=100°,则∠BOC等于( )
A.100° B.80° C.50° D.110°
2.如图,在点A处,有一个牧童在放牛,牛吃饱后要到河边饮水,牧童把牛牵到河边,沿的路径走才能使所走的路程最少,其依据是( )
A.经过一点有无数条直线 B.垂线段最短
C.两点之间,线段最短 D.两点确定一条直线
3.如图所示, 和 是对顶角的是( )
A. B.
C. D.
4.点A为直线BC外一点,AC⊥BC于点C,AC=6.点Р是直线BC上的动点,则线段AP长可能是( )
A.1 B.3 C.5 D.7
5.如图,直线c、b被直线a所截,则∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
6.如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.64° D.72°
7.如图,直线AB、CD相交于点O,若∠1+∠2=100°,则∠BOC等于( )
A.130° B.140° C.150° D.160°
8.两直线被第三条直线所截,∠1与∠2是同旁内角,且∠1=30° ,则∠2的度数为( )
A.150° B.30°
C.30° 或150° D.无法确定
9.如图,下列说法中,错误的是( )
A.∠4与∠B是同位角 B.∠B与∠C是同旁内角
C.∠2与∠C是同位角 D.∠1与∠3是内错角
10.如图,△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,P为直线AB上一动点,连接PC,则线段PC的最小值是( )
A.3 B.2.5 C.2.4 D.2
二、填空题
11.为了测量一座古塔外墙底部的底角的度数,李潇同学设计了如下测量方案:作的延长线,量出的度数,从而得到的度数.这个测量方案的依据是 .
12.如图,,直线过点,若,则的度数是 .
13.如图,在用数字标注的角中,∠4 与 是同位角,与 是内错角,与 是同旁内角。
14.指出图中各对角的位置关系:
(1)∠C和∠D是 角;
(2)∠B和∠GEF是 角;
(3)∠A和∠D是 角;
(4)∠AGE和∠BGE是 角;
(5)∠CFD和∠AFB是 角.
15.如图,直线,被直线所截,若,,,则 .
16.n条水平直线与倾斜直线a相交可得 条线段, 对同位角, 对内错角, 对同旁内角.
三、计算题
17.如图所示,已知,,计算的大小.
18.如图,O为直线AB上一点,OC⊥AB,并且∠AOD=130°.求∠COD的度数.
四、解答题
19.如图,直线AB,CD相交于点O,OM⊥AB,ON⊥CD.
(1)写出图中所有与∠AOC互余的角.
(2)当∠MON=120°时,求∠BOD 的度数.
20.找出图中所有的同位角、内错角和同旁内角。
21.如图,,OB是的平分线,C、O,D在同一条直线上.若,求的度数.
22.如图,直线AB,CD相交于点O,OC平分∠BOE,∠AOE=2∠FOD.
(1)若∠FOD=21°,求∠AOD的度数;
(2)猜想OE与OF的位置关系,并说明理由.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】D
9.【答案】A
10.【答案】C
11.【答案】对顶角相等
12.【答案】
13.【答案】∠1;∠2;∠3 和∠5
14.【答案】同旁内;同位;内错;邻补;对顶
15.【答案】
16.【答案】;2n(n﹣1);n(n﹣1);n(n﹣1)
17.【答案】
18.【答案】解:∵∠AOD=130°,
∴∠BOD=180°-∠AOD-80°-130°=50°.
∵OC⊥AB,
∴∠BOC=90°.
∴∠COD=∠BOD+∠BOC=50°+90°=140°.
19.【答案】(1)解:∠COM,∠AON
(2)解:60°
20.【答案】解:同位角:∠A与∠EDC,∠C 与∠ABF;
内错角:∠EDC与∠C,∠A与∠ABF;
同旁内角:∠A 与∠ABC,∠A 与∠ADC,∠C 与∠ABC,∠C与∠ADC
21.【答案】解:因为OB是的平分线,且,所以.
又因为,所以,
所以.
22.【答案】(1)解:∵∠FOD=21°,∠AOE=2∠FOD,∴∠AOE=42°,∴∠BOE=180°-∠AOE=180°-42°=138°.
∵OC平分∠BOE,∴∠BOC=-∠BOE=-×138°=69°,∴∠AOD=∠BOC=69°;
(2)解:猜想OE⊥OF,理由如下:
设∠DOF=x,则∠AOE=2x.
∴∠BOE=180°-2x.
∵OC平分∠BOE,
∴.
∴∠AOD=∠BOC=90°-x.
∴∠AOF=∠AOD-∠DOF=90°-2x.
∴∠EOF=∠AOE+∠AOF=2x+90°-2x=90°.
∴OE⊥OF.
21世纪教育网(www.21cnjy.com)
1 / 7
同课章节目录
