7.1相交线(培优)综合检测题 同步练习(含答案)
文档属性
| 名称 | 7.1相交线(培优)综合检测题 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 351.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
7.1相交线(培优)综合检测题
一、单选题
1.将一副直角三角板按如图所示摆放,,,,则下列结论不正确的是( )
A. B. C. D.
2.如图,在锐角三角形中,,的面积为8,平分.若、分别是、上的动点,则的最小值是( )
A.3 B.4 C.5 D.6
3.下列说法正确的是( )
A.相等的两个角是对顶角
B.过一点有且只有一条直线与已知直线平行
C.直线外一点与直线上各点连接的所有线段中,垂线段最短
D.过一点有且只有一条直线与已知直线垂直
4.如图,河道的一侧有甲、乙两个村庄,现要铺设一条管道将水引向甲、乙两村,下列四种方案中最节省材料的是( )
A. B.
C. D.
5.如图,下列说法中不正确的是( )
A.和是同旁内角 B.和是内错角
C.和是同位角 D.和是对顶角
6.如图,,垂足分别为A,D,图中互余的角共有( )
A.2对 B.3对 C.4对 D.5对
7.如图, 直线 相交于点 , 下列命题中, 是真命题的是( )
A.若 , 则
B.若 , 则 与 互为对顶角
C.若 , 则
D.若 , 则 与 互为邻补角
8.下列说法中正确的是( )
A.有且只有一条直线与已知直线垂直;
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线距离;
C.互相垂直的两条线段一定相交;
D.直线外一点与直线上各点连接而成的所有线段中,最短线段的长度是,则点到直线的距离是.
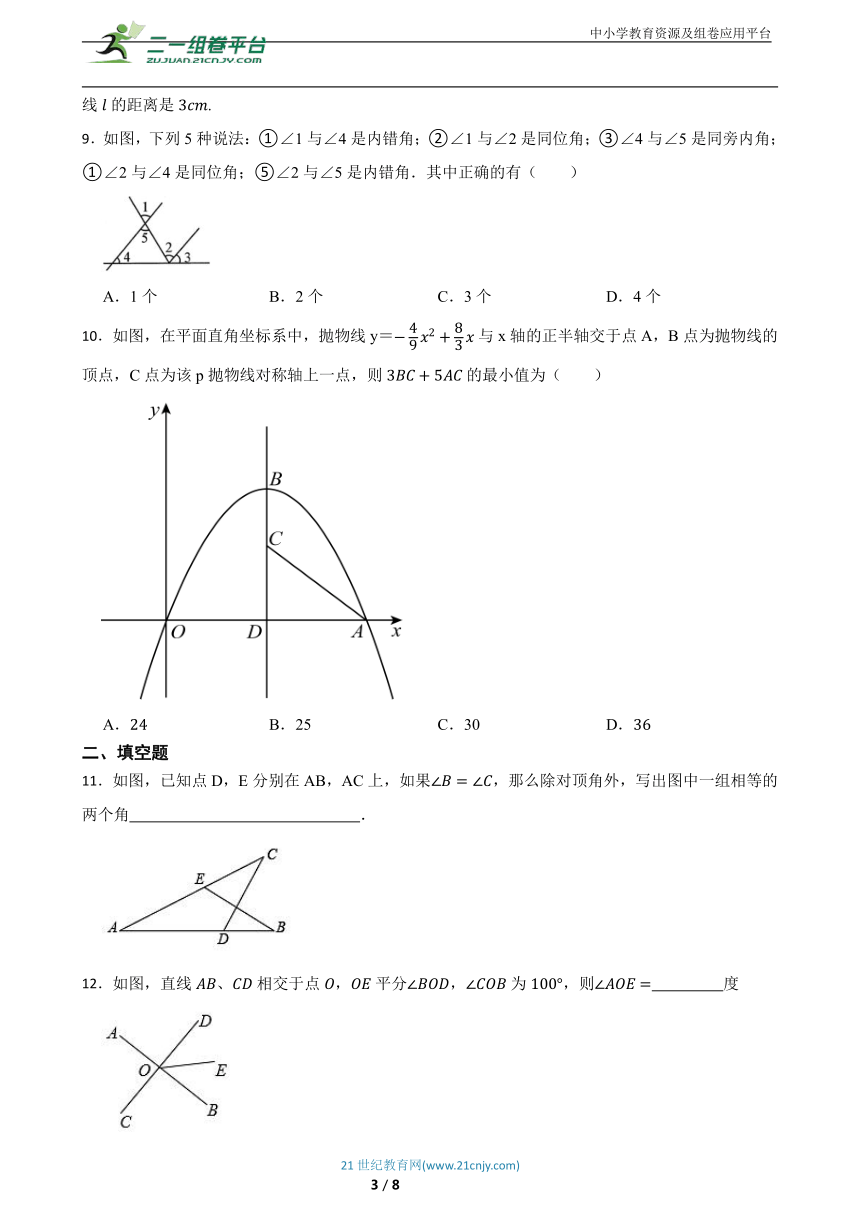
9.如图,下列5种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠4与∠5是同旁内角;①∠2与∠4是同位角;⑤∠2与∠5是内错角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在平面直角坐标系中,抛物线y=与x轴的正半轴交于点A,B点为抛物线的顶点,C点为该p抛物线对称轴上一点,则的最小值为( )
A. B.25 C.30 D.
二、填空题
11.如图,已知点D,E分别在AB,AC上,如果,那么除对顶角外,写出图中一组相等的两个角 .
12.如图,直线、相交于点,平分,为,则 度
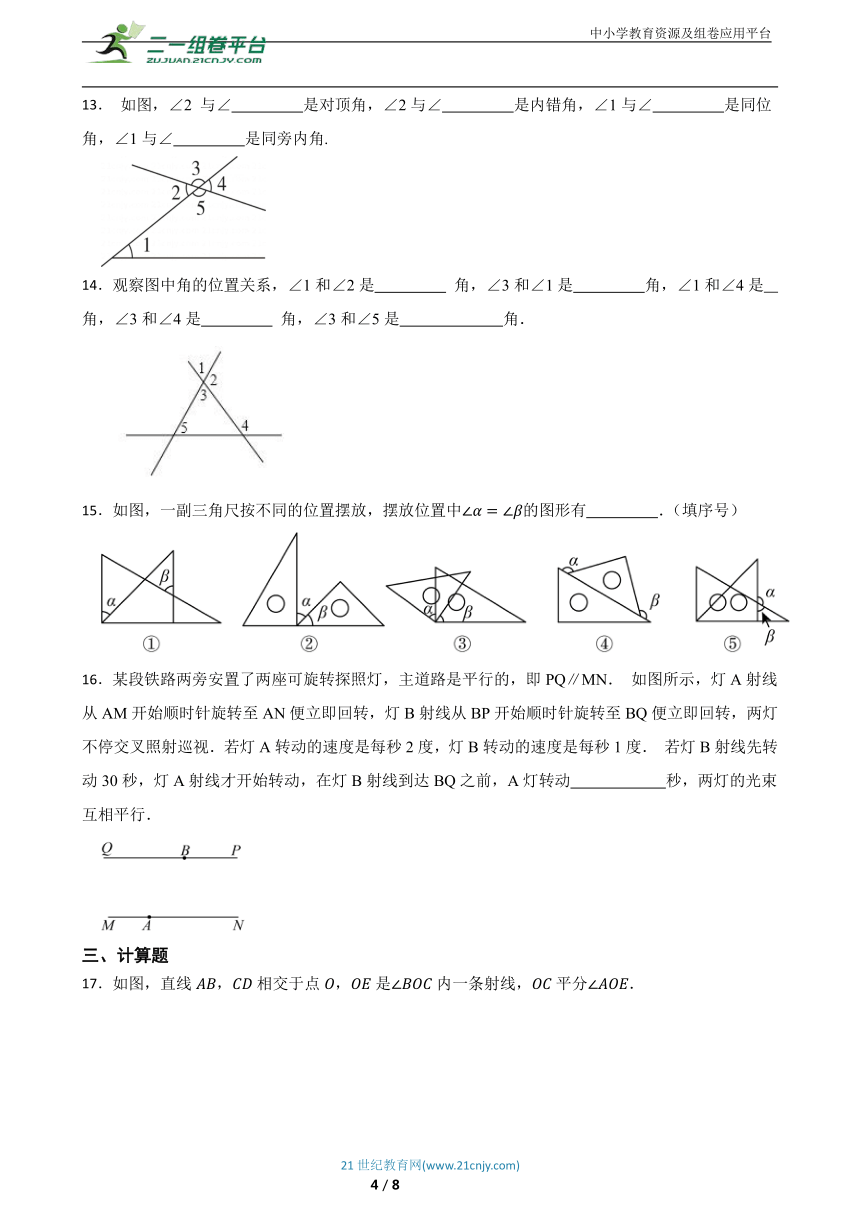
13. 如图,∠2 与∠ 是对顶角,∠2与∠ 是内错角,∠1与∠ 是同位角,∠1与∠ 是同旁内角.
14.观察图中角的位置关系,∠1和∠2是 角,∠3和∠1是 角,∠1和∠4是 角,∠3和∠4是 角,∠3和∠5是 角.
15.如图,一副三角尺按不同的位置摆放,摆放位置中的图形有 .(填序号)
16.某段铁路两旁安置了两座可旋转探照灯,主道路是平行的,即PQ∥MN. 如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度. 若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动 秒,两灯的光束互相平行.
三、计算题
17.如图,直线,相交于点,是内一条射线,平分.
(1)若,求的度数.
(2)若比大,求的度数.
18.如图,直线,相交于点,于点,■°.
(1)若“■”表示120,求的度数.
(2)若求得,则“■”中的数字是多少?
四、解答题
19.如图,直线、相交于点,,.
(1)写出图中的余角______;
(2)如果,求的度数.
20.如图,,,,求的度数.
21.如图,直线、相交于点O,,平分.
(1)若,求的度数;
(2)若比大24°,求的度数.
22.如图,已知点C在线段上,射线交直线于点O,平分.
(1)若,求的度数.
(2)若,且,求证:.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】C
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】∠BDO=∠CEO或∠ADC=∠AEB
12.【答案】
13.【答案】4;1;4;5
14.【答案】邻补;对顶;同位;内错;同旁内角
15.【答案】②③④
16.【答案】30或110
17.【答案】(1)
(2)
18.【答案】(1)150°
(2)140
19.【答案】(1),,
(2)
20.【答案】
21.【答案】(1)解:,,
平分,,
,,
的度数为56°;
(2)解:设,比大24°,
平分,,
,,
,解得:
,,
的度数为142°.
22.【答案】(1)解:∵平分,,
∴,
∴;
(2)证明:∵,,且,
∴,
∵,
∴,
∴,即,
∴.
21世纪教育网(www.21cnjy.com)
2 / 8
7.1相交线(培优)综合检测题
一、单选题
1.将一副直角三角板按如图所示摆放,,,,则下列结论不正确的是( )
A. B. C. D.
2.如图,在锐角三角形中,,的面积为8,平分.若、分别是、上的动点,则的最小值是( )
A.3 B.4 C.5 D.6
3.下列说法正确的是( )
A.相等的两个角是对顶角
B.过一点有且只有一条直线与已知直线平行
C.直线外一点与直线上各点连接的所有线段中,垂线段最短
D.过一点有且只有一条直线与已知直线垂直
4.如图,河道的一侧有甲、乙两个村庄,现要铺设一条管道将水引向甲、乙两村,下列四种方案中最节省材料的是( )
A. B.
C. D.
5.如图,下列说法中不正确的是( )
A.和是同旁内角 B.和是内错角
C.和是同位角 D.和是对顶角
6.如图,,垂足分别为A,D,图中互余的角共有( )
A.2对 B.3对 C.4对 D.5对
7.如图, 直线 相交于点 , 下列命题中, 是真命题的是( )
A.若 , 则
B.若 , 则 与 互为对顶角
C.若 , 则
D.若 , 则 与 互为邻补角
8.下列说法中正确的是( )
A.有且只有一条直线与已知直线垂直;
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线距离;
C.互相垂直的两条线段一定相交;
D.直线外一点与直线上各点连接而成的所有线段中,最短线段的长度是,则点到直线的距离是.
9.如图,下列5种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠4与∠5是同旁内角;①∠2与∠4是同位角;⑤∠2与∠5是内错角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在平面直角坐标系中,抛物线y=与x轴的正半轴交于点A,B点为抛物线的顶点,C点为该p抛物线对称轴上一点,则的最小值为( )
A. B.25 C.30 D.
二、填空题
11.如图,已知点D,E分别在AB,AC上,如果,那么除对顶角外,写出图中一组相等的两个角 .
12.如图,直线、相交于点,平分,为,则 度
13. 如图,∠2 与∠ 是对顶角,∠2与∠ 是内错角,∠1与∠ 是同位角,∠1与∠ 是同旁内角.
14.观察图中角的位置关系,∠1和∠2是 角,∠3和∠1是 角,∠1和∠4是 角,∠3和∠4是 角,∠3和∠5是 角.
15.如图,一副三角尺按不同的位置摆放,摆放位置中的图形有 .(填序号)
16.某段铁路两旁安置了两座可旋转探照灯,主道路是平行的,即PQ∥MN. 如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度. 若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动 秒,两灯的光束互相平行.
三、计算题
17.如图,直线,相交于点,是内一条射线,平分.
(1)若,求的度数.
(2)若比大,求的度数.
18.如图,直线,相交于点,于点,■°.
(1)若“■”表示120,求的度数.
(2)若求得,则“■”中的数字是多少?
四、解答题
19.如图,直线、相交于点,,.
(1)写出图中的余角______;
(2)如果,求的度数.
20.如图,,,,求的度数.
21.如图,直线、相交于点O,,平分.
(1)若,求的度数;
(2)若比大24°,求的度数.
22.如图,已知点C在线段上,射线交直线于点O,平分.
(1)若,求的度数.
(2)若,且,求证:.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】C
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】∠BDO=∠CEO或∠ADC=∠AEB
12.【答案】
13.【答案】4;1;4;5
14.【答案】邻补;对顶;同位;内错;同旁内角
15.【答案】②③④
16.【答案】30或110
17.【答案】(1)
(2)
18.【答案】(1)150°
(2)140
19.【答案】(1),,
(2)
20.【答案】
21.【答案】(1)解:,,
平分,,
,,
的度数为56°;
(2)解:设,比大24°,
平分,,
,,
,解得:
,,
的度数为142°.
22.【答案】(1)解:∵平分,,
∴,
∴;
(2)证明:∵,,且,
∴,
∵,
∴,
∴,即,
∴.
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
