3.6 直线与圆的位置关系(第1课时)(共14张PPT)2024-2025学年北师大版九年级下册
文档属性
| 名称 | 3.6 直线与圆的位置关系(第1课时)(共14张PPT)2024-2025学年北师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 288.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 22:30:00 | ||
图片预览

文档简介
(共14张PPT)
第三章
圆
直线和圆的位置关系
(第1课时)
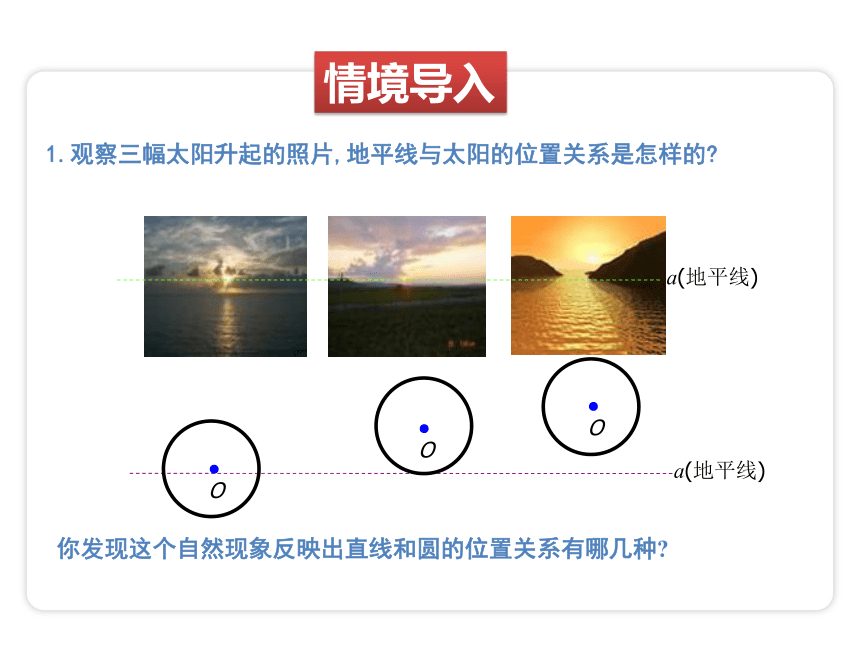
1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
你发现这个自然现象反映出直线和圆的位置关系有哪几种
a(地平线)
a(地平线)
●O
●O
●O
情境导入
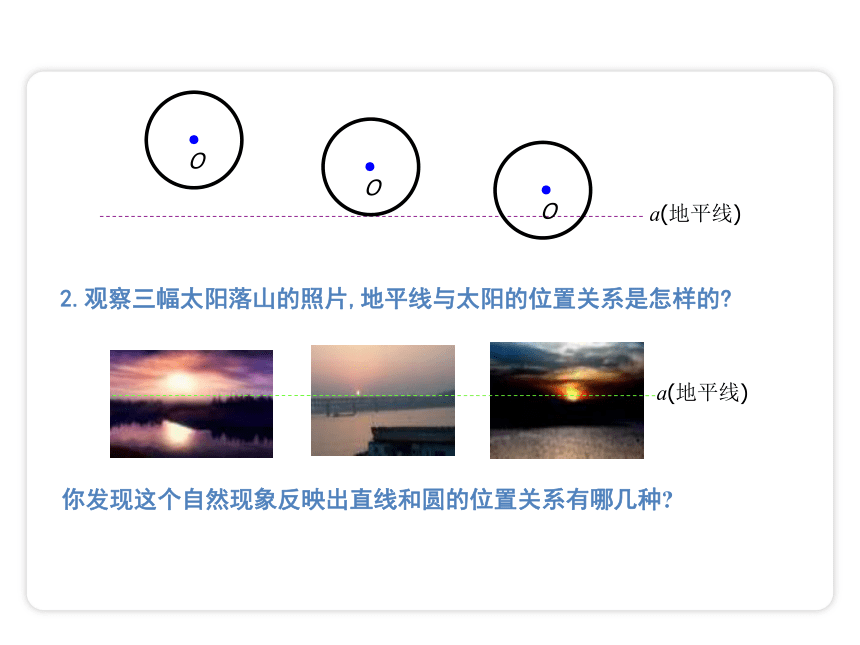
2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
你发现这个自然现象反映出直线和圆的位置关系有哪几种
a(地平线)
a(地平线)
●O
●O
●O
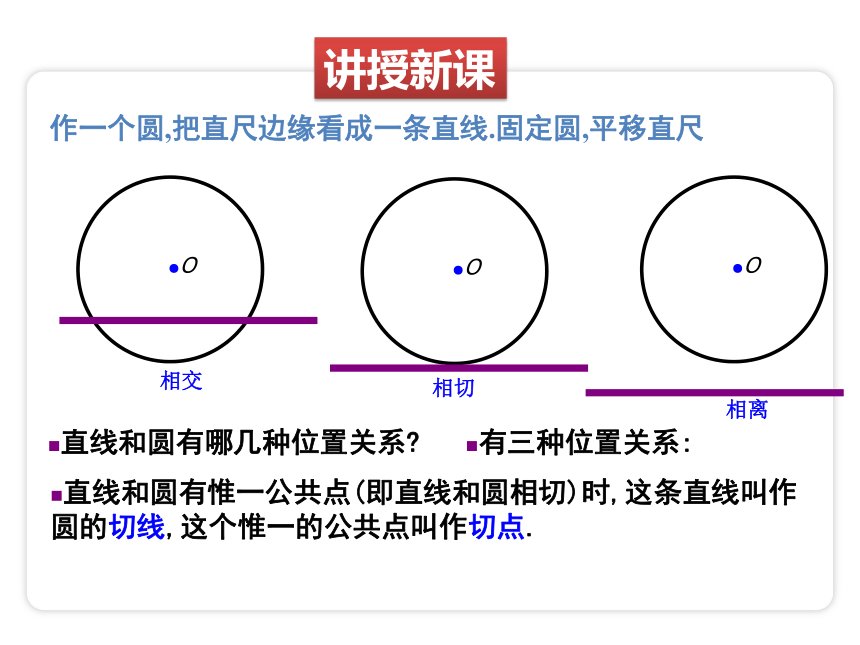
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺
直线和圆有哪几种位置关系
●O
●O
有三种位置关系:
相交
直线和圆有惟一公共点(即直线和圆相切)时,这条直线叫作圆的切线,这个惟一的公共点叫作切点.
●O
相切
相离
讲授新课
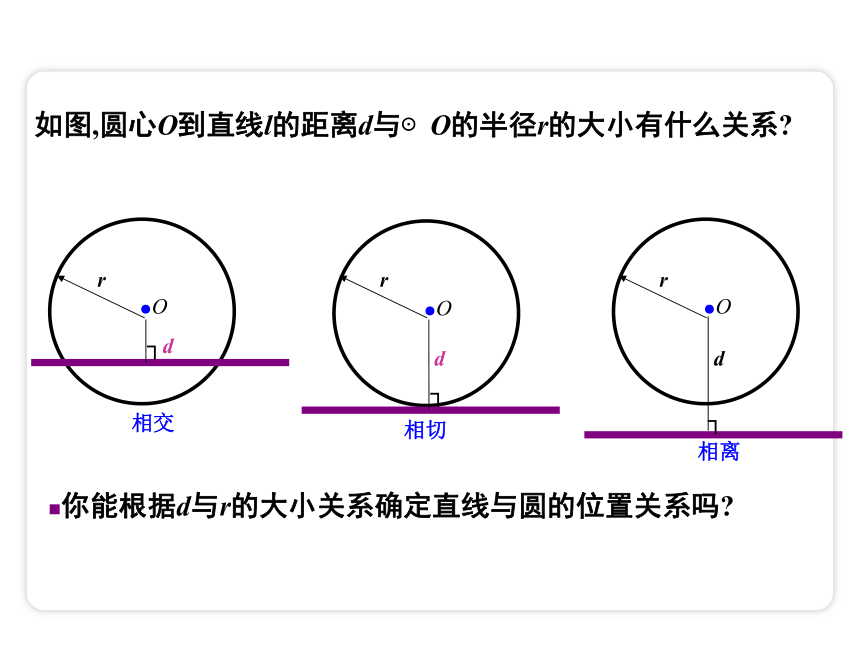
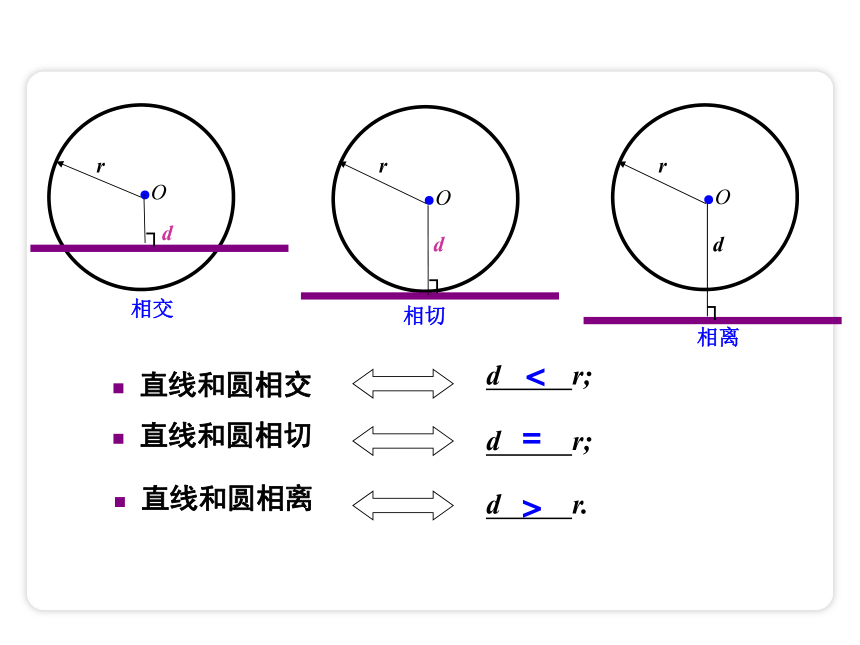
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系
你能根据d与r的大小关系确定直线与圆的位置关系吗
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
d r;
d r;
直线和圆相切
直线和圆相离
d r.
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
直线和圆相交
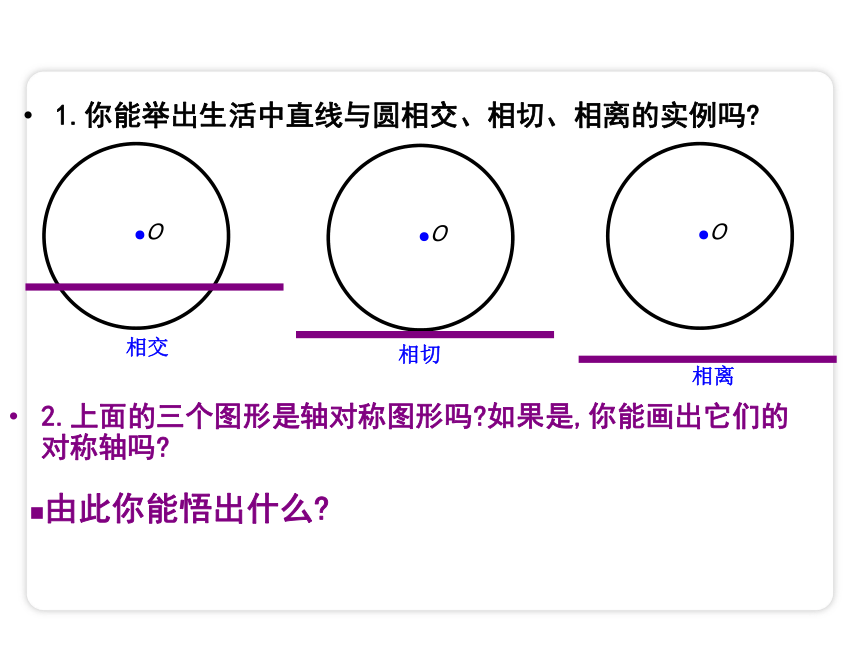
1.你能举出生活中直线与圆相交、相切、相离的实例吗
2.上面的三个图形是轴对称图形吗 如果是,你能画出它们的对称轴吗
由此你能悟出什么
●O
●O
相交
●O
相切
相离
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
直径AB垂直于直线CD.
老师期望:
圆的对称性已经在你心中落地生根.
小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此∠BAC=∠BAD=90°.
C
D
B
●O
A
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
则OMC
D
B
●O
A
所以AB与CD垂直.
M
参考小颖和小亮的说理过程,请你写出这个命题
定理 圆的切线垂直于过切点的半径.
老师提示:
切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.
如图,∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.
C
D
B
● O
A
例1 已知Rt△ABC的斜边AB=8 cm,直角边AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切
老师提示:
模型“双垂直三角形”你可曾认识.
A
C
B
┐
解:(1)过点C作CD⊥AB于D.
D
┛
AB=8 cm,AC=4 cm.
∴∠A=60°.
因此,当半径长为 cm时,AB与⊙C相切.
例题讲解
例1 已知Rt△ABC的斜边AB=8 cm,直角边AC=4 cm.
(2)以点C为圆心,分别以2 cm,4 cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系
当r=4 cm时,dA
C
B
┐
D
┛
当r=2 cm时,d>r,AB与⊙C相离;
解:(2)由(1)可知,圆心到AB的距离d= cm,所以
1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围.
2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少
老师提示:硬币滚动一圈,圆心经过的路径是与直线平行的一条线段,其长度等于圆的周长.
r
B
C
●O
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
随堂练习
谢谢观看
第三章
圆
直线和圆的位置关系
(第1课时)
1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
你发现这个自然现象反映出直线和圆的位置关系有哪几种
a(地平线)
a(地平线)
●O
●O
●O
情境导入
2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
你发现这个自然现象反映出直线和圆的位置关系有哪几种
a(地平线)
a(地平线)
●O
●O
●O
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺
直线和圆有哪几种位置关系
●O
●O
有三种位置关系:
相交
直线和圆有惟一公共点(即直线和圆相切)时,这条直线叫作圆的切线,这个惟一的公共点叫作切点.
●O
相切
相离
讲授新课
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系
你能根据d与r的大小关系确定直线与圆的位置关系吗
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
d r;
d r;
直线和圆相切
直线和圆相离
d r.
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
直线和圆相交
1.你能举出生活中直线与圆相交、相切、相离的实例吗
2.上面的三个图形是轴对称图形吗 如果是,你能画出它们的对称轴吗
由此你能悟出什么
●O
●O
相交
●O
相切
相离
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
直径AB垂直于直线CD.
老师期望:
圆的对称性已经在你心中落地生根.
小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此∠BAC=∠BAD=90°.
C
D
B
●O
A
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
则OM
D
B
●O
A
所以AB与CD垂直.
M
参考小颖和小亮的说理过程,请你写出这个命题
定理 圆的切线垂直于过切点的半径.
老师提示:
切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.
如图,∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.
C
D
B
● O
A
例1 已知Rt△ABC的斜边AB=8 cm,直角边AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切
老师提示:
模型“双垂直三角形”你可曾认识.
A
C
B
┐
解:(1)过点C作CD⊥AB于D.
D
┛
AB=8 cm,AC=4 cm.
∴∠A=60°.
因此,当半径长为 cm时,AB与⊙C相切.
例题讲解
例1 已知Rt△ABC的斜边AB=8 cm,直角边AC=4 cm.
(2)以点C为圆心,分别以2 cm,4 cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系
当r=4 cm时,d
C
B
┐
D
┛
当r=2 cm时,d>r,AB与⊙C相离;
解:(2)由(1)可知,圆心到AB的距离d= cm,所以
1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围.
2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少
老师提示:硬币滚动一圈,圆心经过的路径是与直线平行的一条线段,其长度等于圆的周长.
r
B
C
●O
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
随堂练习
谢谢观看
