人教版 五年级上册数学 两端都不栽的植树问题(课件)(共21张PPT)
文档属性
| 名称 | 人教版 五年级上册数学 两端都不栽的植树问题(课件)(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 14:35:28 | ||
图片预览






文档简介
(共21张PPT)
数学广角——植树问题
两端都不栽的植树问题
1.理解间隔数与棵数之间的关系并应用到生活中去。(重点)
2.通过画图发现在一条线段上两端都不栽的植树问题的规律。
学习目标
动物园里的大象馆和猴山相距 60 m。绿化队要在两馆间的小路两旁栽树(两端都不栽),相邻两棵树之间的距离是 3 m。一共要栽多少棵树?
从题目中你了解哪些信息?
知条件:
小路的全长是_______。
小树之间的间隔是______。
要求的是________的总数。
60m
3m
植树
60m
3m
两端不栽的算法和两端都栽的算法一样吗?我们也先画一个简单的图来看看。
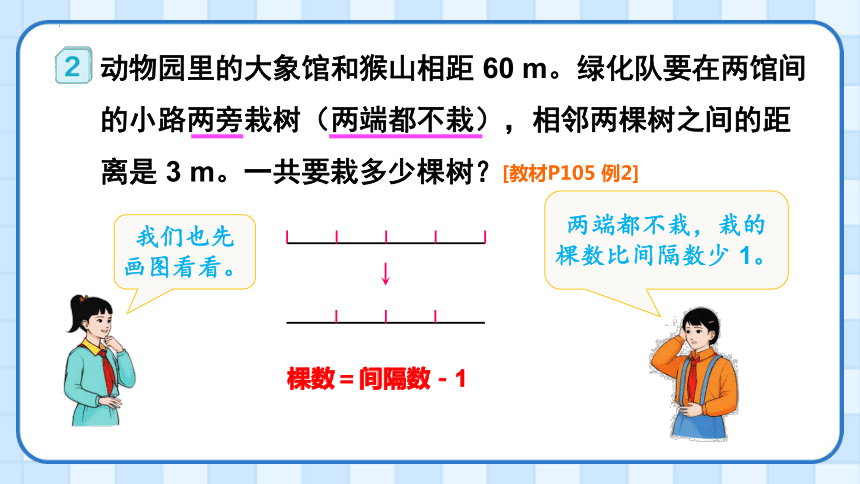
我们也先画图看看。
棵数=间隔数-1
两端都不栽,栽的棵数比间隔数少 1。
动物园里的大象馆和猴山相距 60 m。绿化队要在两馆间的小路两旁栽树(两端都不栽),相邻两棵树之间的距离是 3 m。一共要栽多少棵树?
[教材P105 例2]
想一想,少的“1”去哪里了
两端都不栽的比两端都栽的少两端的两棵。
两端都不栽的植树棵数=间隔数+1-2=间隔数-1。
答:一共要栽 棵树。
60÷3 = 20
( )× 2 =( )
20 ( )=( )
19 38
- 1 19
38
小路两旁都要栽树,所以还要乘2。
规范答:
解:
间隔数:60÷3=20(个)
一边的植树数:20 1=19(棵)
答:一共要栽38棵树。
一共植树数:19×2=38(棵)
植树问题通常是指沿着一定的路线植树,这条路线被树平分成若干段(间隔),由于路线或植树要求的不同,路线的总长度与路线被分成的段数(间隔数)和植树的棵树之间的关系就不同。
小明家门前有一条 35 m 长的小路,绿化队要在小路一旁栽一排树。每隔 5 m 栽一棵树(一端栽,一端不栽)。一共要栽多少棵?
间隔数和植树棵数恰好一一对应。
总路长÷植株间距=间隔数=植树棵数
35 ÷ 5 = 7(棵)
答:一共要栽 7 棵树。
35 m
5 m
5 m
5 m
5 m
5 m
5 m
5 m
做完后,可以画线段图验证一下。
想一想,植树问题有哪几种情况?每种情况中棵数与间隔数之间是什么关系?
两端都栽
棵数=间隔数+1
想一想,植树问题有哪几种情况?每种情况中棵数与间隔数之间是什么关系?
两端都不栽
一端栽,一端不栽
棵数=间隔数-1
棵数=间隔数
1.在一条全长2km的街道两旁安装路灯(两端都要安装),每隔50m安一盏。一共要安装多少盏路灯?
2 km = 2000 m
间隔数:2000÷50 = 40(个)
盏数:(40+1)×2 = 82(盏)
答:一共要安装82盏路灯。
盏数=间隔数+1
2.一根木头长10 m,要把它平均锯成5段。每锯下一段需要8分钟,锯完一共要花多少分钟
5 - 1 = 4(次)
8×4 = 32(分)
答:一共要花32分钟。
锯1次
锯成2段
锯2次
锯成3段
锯3次
锯成4段
……
……
锯的次数=锯的段数-1
两端都不栽的植树问题
小明和小军同住一幢楼,小明住在四楼,小军住在七楼。小明回家要走60级台阶,小军回家要走多少级台阶?(每相邻两层之间的台阶数相同)
3.
答:小军回家要走120级。
每层台阶数:60÷ (4 1)=20(级)
解:
小军要走的台阶数:20×(7 1)=120(级)
4.学校门前有一条笔直的小路,在小路的一旁从一头
到另一头每隔 3 m栽一棵树,两端都不栽,一共栽
了 18 棵,这条小路长多少米?
两端都不植树:间隔数=棵数+1
3×(18+1)= 57(m)
答:这条小路长 57 m。
5、两座楼房之间相距 112 m,每 8 m 栽一棵松树(两端都不栽),一共能栽多少棵松树?
112÷8-1 = 13(棵)
答:一共能栽13棵松树。
间隔数:100÷5 = 20(辆)
标志数:20-1 = 19(个)
答:最多可停放20辆车, 需要画19个“⊥”标志。
如果把“⊥”标志看作树的话,这就是一道两端都不栽的植树问题。
6.某小区物业人员在小区路的一边每隔5米安置一个车位,并用“⊥”标志隔开。在一段100米的路边最多可停多少辆车?需要画几个“⊥”标志?
⊥
⊥
⊥
⊥
⊥
⊥
⊥
⊥
这节课你有什么收获?
在一条路线上植树(两端都不栽和只栽一端)
(两端都不栽)
间隔数=总路长÷植株间距,
植树棵数=间隔数-1 ,
(只栽一端)
植树棵数=间隔数=总路长÷植株间距。
数学广角——植树问题
两端都不栽的植树问题
1.理解间隔数与棵数之间的关系并应用到生活中去。(重点)
2.通过画图发现在一条线段上两端都不栽的植树问题的规律。
学习目标
动物园里的大象馆和猴山相距 60 m。绿化队要在两馆间的小路两旁栽树(两端都不栽),相邻两棵树之间的距离是 3 m。一共要栽多少棵树?
从题目中你了解哪些信息?
知条件:
小路的全长是_______。
小树之间的间隔是______。
要求的是________的总数。
60m
3m
植树
60m
3m
两端不栽的算法和两端都栽的算法一样吗?我们也先画一个简单的图来看看。
我们也先画图看看。
棵数=间隔数-1
两端都不栽,栽的棵数比间隔数少 1。
动物园里的大象馆和猴山相距 60 m。绿化队要在两馆间的小路两旁栽树(两端都不栽),相邻两棵树之间的距离是 3 m。一共要栽多少棵树?
[教材P105 例2]
想一想,少的“1”去哪里了
两端都不栽的比两端都栽的少两端的两棵。
两端都不栽的植树棵数=间隔数+1-2=间隔数-1。
答:一共要栽 棵树。
60÷3 = 20
( )× 2 =( )
20 ( )=( )
19 38
- 1 19
38
小路两旁都要栽树,所以还要乘2。
规范答:
解:
间隔数:60÷3=20(个)
一边的植树数:20 1=19(棵)
答:一共要栽38棵树。
一共植树数:19×2=38(棵)
植树问题通常是指沿着一定的路线植树,这条路线被树平分成若干段(间隔),由于路线或植树要求的不同,路线的总长度与路线被分成的段数(间隔数)和植树的棵树之间的关系就不同。
小明家门前有一条 35 m 长的小路,绿化队要在小路一旁栽一排树。每隔 5 m 栽一棵树(一端栽,一端不栽)。一共要栽多少棵?
间隔数和植树棵数恰好一一对应。
总路长÷植株间距=间隔数=植树棵数
35 ÷ 5 = 7(棵)
答:一共要栽 7 棵树。
35 m
5 m
5 m
5 m
5 m
5 m
5 m
5 m
做完后,可以画线段图验证一下。
想一想,植树问题有哪几种情况?每种情况中棵数与间隔数之间是什么关系?
两端都栽
棵数=间隔数+1
想一想,植树问题有哪几种情况?每种情况中棵数与间隔数之间是什么关系?
两端都不栽
一端栽,一端不栽
棵数=间隔数-1
棵数=间隔数
1.在一条全长2km的街道两旁安装路灯(两端都要安装),每隔50m安一盏。一共要安装多少盏路灯?
2 km = 2000 m
间隔数:2000÷50 = 40(个)
盏数:(40+1)×2 = 82(盏)
答:一共要安装82盏路灯。
盏数=间隔数+1
2.一根木头长10 m,要把它平均锯成5段。每锯下一段需要8分钟,锯完一共要花多少分钟
5 - 1 = 4(次)
8×4 = 32(分)
答:一共要花32分钟。
锯1次
锯成2段
锯2次
锯成3段
锯3次
锯成4段
……
……
锯的次数=锯的段数-1
两端都不栽的植树问题
小明和小军同住一幢楼,小明住在四楼,小军住在七楼。小明回家要走60级台阶,小军回家要走多少级台阶?(每相邻两层之间的台阶数相同)
3.
答:小军回家要走120级。
每层台阶数:60÷ (4 1)=20(级)
解:
小军要走的台阶数:20×(7 1)=120(级)
4.学校门前有一条笔直的小路,在小路的一旁从一头
到另一头每隔 3 m栽一棵树,两端都不栽,一共栽
了 18 棵,这条小路长多少米?
两端都不植树:间隔数=棵数+1
3×(18+1)= 57(m)
答:这条小路长 57 m。
5、两座楼房之间相距 112 m,每 8 m 栽一棵松树(两端都不栽),一共能栽多少棵松树?
112÷8-1 = 13(棵)
答:一共能栽13棵松树。
间隔数:100÷5 = 20(辆)
标志数:20-1 = 19(个)
答:最多可停放20辆车, 需要画19个“⊥”标志。
如果把“⊥”标志看作树的话,这就是一道两端都不栽的植树问题。
6.某小区物业人员在小区路的一边每隔5米安置一个车位,并用“⊥”标志隔开。在一段100米的路边最多可停多少辆车?需要画几个“⊥”标志?
⊥
⊥
⊥
⊥
⊥
⊥
⊥
⊥
这节课你有什么收获?
在一条路线上植树(两端都不栽和只栽一端)
(两端都不栽)
间隔数=总路长÷植株间距,
植树棵数=间隔数-1 ,
(只栽一端)
植树棵数=间隔数=总路长÷植株间距。
