冀教版 数学六年级上册 5.1一般应用问题 (课件)(共33张PPT)
文档属性
| 名称 | 冀教版 数学六年级上册 5.1一般应用问题 (课件)(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 289.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 15:14:38 | ||
图片预览






文档简介
(共33张PPT)
(冀教版·六年级·上册)
5.1一般应用问题
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
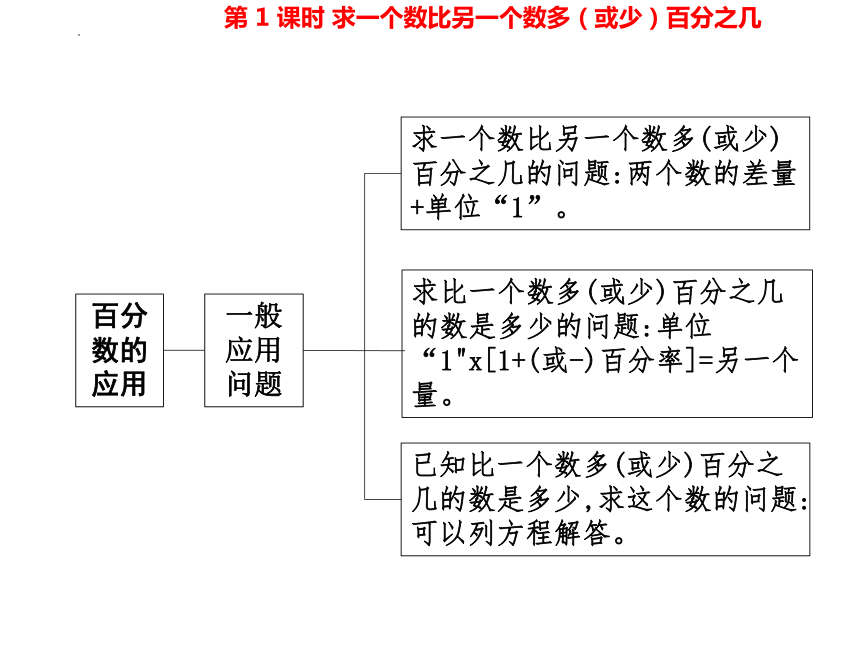
一般应用问题
求一个数比另一个数多(或少)百分之几的问题:两个数的差量+单位“1”。
已知比一个数多(或少)百分之几的数是多少,求这个数的问题:可以列方程解答。
求比一个数多(或少)百分之几的数是多少的问题:单位“1"x[1+(或-)百分率]=另一个量。
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
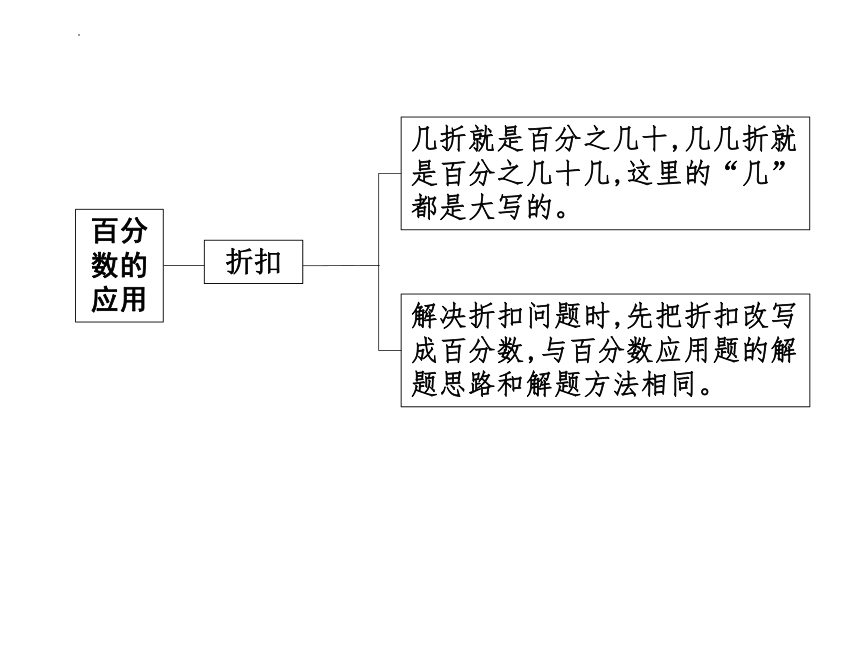
折扣
几折就是百分之几十,几几折就是百分之几十几,这里的“几”都是大写的。
解决折扣问题时,先把折扣改写成百分数,与百分数应用题的解题思路和解题方法相同。
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
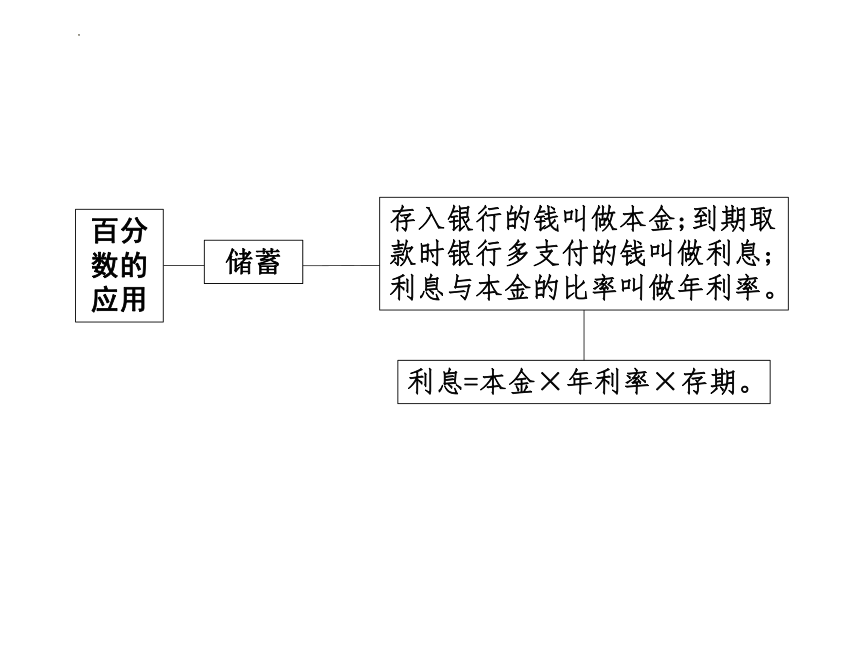
储蓄
存入银行的钱叫做本金;到期取款时银行多支付的钱叫做利息;利息与本金的比率叫做年利率。
利息=本金×年利率×存期。
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
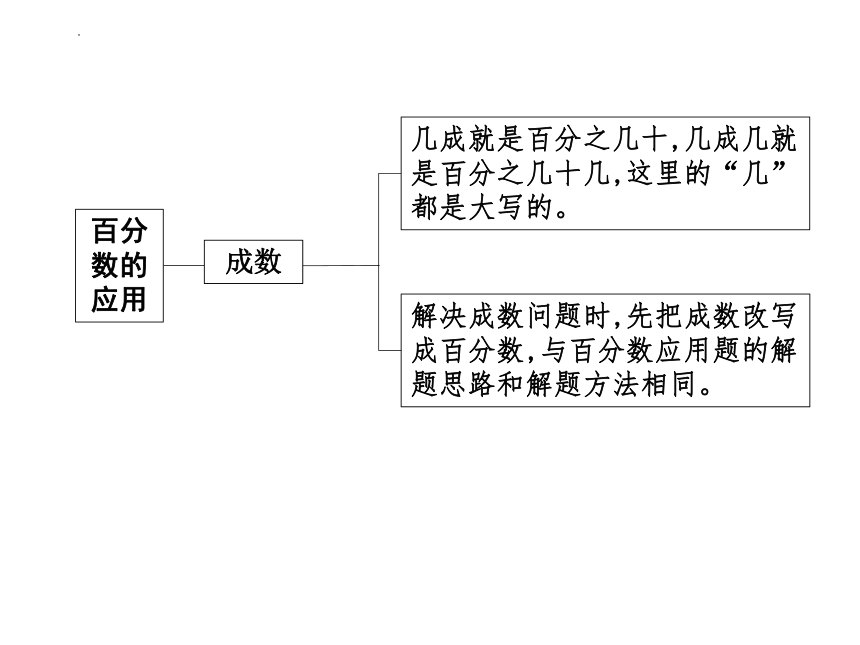
成数
几成就是百分之几十,几成几就是百分之几十几,这里的“几”都是大写的。
解决成数问题时,先把成数改写成百分数,与百分数应用题的解题思路和解题方法相同。
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
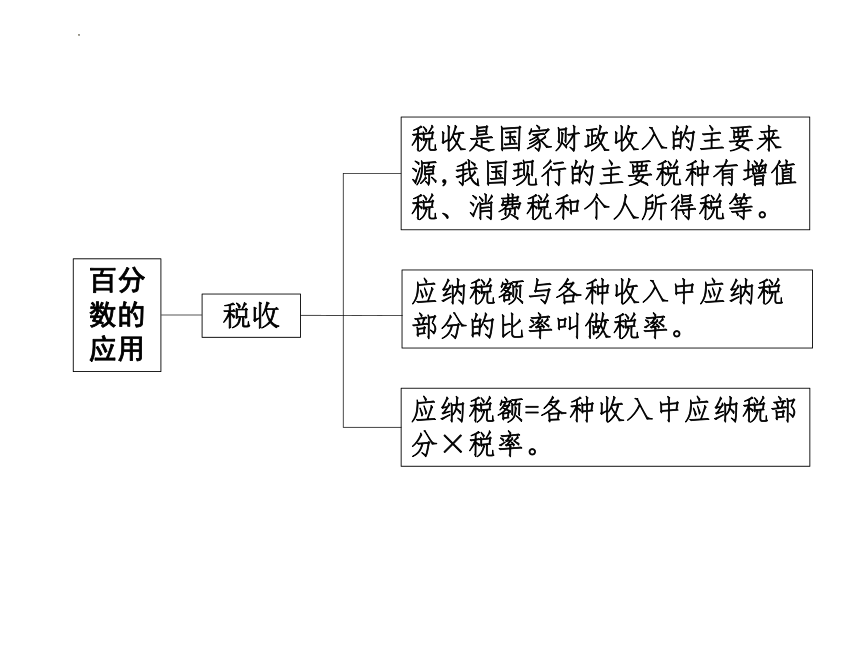
税收
税收是国家财政收入的主要来源,我国现行的主要税种有增值税、消费税和个人所得税等。
应纳税额=各种收入中应纳税部分×税率。
应纳税额与各种收入中应纳税部分的比率叫做税率。
■考点 求一个数比另-个数多(或少)百分之几
第 1 课时 求一个数比另一个数多(或少)百分之几
1.求一个数比另一个数多(或少)百分之几,实际上也是求一个数是另一个数的百分之几,即两个数的差量占另一个数(即单位“1”的量)的百分之几。
2.用甲表示一个数,用乙表示另一个数:
(1)求甲比乙多百分之儿的方法:(甲-乙)÷乙或甲÷乙-100%;
(2)求乙比甲少百分之几的方法:(甲-乙)÷甲或100%-乙÷甲。
第 1 课时 求一个数比另一个数多(或少)百分之几
3.在实际生活中,人们常用“增加百分之几”“减少百分之几”“节约百分之几”等来表示增加、减少的幅度。“增加百分之几”表示增加的是原来的百分之几,“减少百分之几”表示减少的是原来的百分之几,“节约百分之几”表示节约的是原来的百分之几。
第 1 课时 求一个数比另一个数多(或少)百分之几
重难突破
解决这类题的关键是什么
答:关键是找准单位“1”,一般“比”字后面是单位“1”的量,两个数的差就是比较量。用比较量作被除数,用单位“1”的量作除数。
例 1 关西小学去年在校学生人数是900人,今年增加到了1080人。今年的在校学生人数比去年在校的人数增加了百分之几
第 1 课时 求一个数比另一个数多(或少)百分之几
[解析]
第 1 课时 求一个数比另一个数多(或少)百分之几
[答案] 方法一:(1080-900)÷900=20%
方法二:1080÷900=120%
120%-100%=20%
答:今年在校学生人数比去年在校的人数增加了20%。
第 1 课时 求一个数比另一个数多(或少)百分之几
例 2 一款笔记本电脑的原价是4000元,降价后的售价为3500元。现价比原价降低了百分之几
第 1 课时 求一个数比另一个数多(或少)百分之几
[解析]
[答案] 方法一:(4000-3500)÷4000=12.5%
方法二:1-3500÷4000=12.5%
答:现价比原价降低了12.5%。
第 1 课时 求一个数比另一个数多(或少)百分之几
■易错易混分析 没有找准单位“1”
第 1 课时 求一个数比另一个数多(或少)百分之几
例3 甲数:乙数=5:4,甲数比乙数多25%,那么乙数比甲数少( )%。
[解析]第一句中“比”字后面是乙数,把乙数看作单位“1”,甲数比乙数多(5-4)÷4=25%。求乙数比甲数少百分之几,是把甲数看作单位“1”,列式计算为(5-4)÷5=20%。
[答案] 20
易错警示:当存在两个单位“1”时,要根据不同的单位“1”进行分析,在不同的单位“1”下作比较,结果是不同的。
■考点一 求比一个数多(或少)百分之几的数是多少
第 2 课时 求具体数量的问题
1.求比一个数多(或少)百分之几的数是多少的问题的特点是单位“1”的量已知。
2.解题方法:方法一:单位“1”的量+(或-)单位“1”的量×另一个量比单位“1”的量多(或少)的百分率=另一个量;
方法二:单位“1”的量×[1+(或-)另一个量比单位“1”的量多(或少)的百分率] =另一个量。
3.“求比一个数多(或少)百分之几的数是多少”的问题的解法和“求比一个数多(或少)几分之几的数是多少”的解法相同,唯一的区别就是把几分之几变成了百分之几。
第 2 课时 求具体数量的问题
重难突破
解决这类问题应该注意什么
答:算出多(或少)的百分之几的数后要记得与原单位“1”相加(相减)。
例 1 一个修路队第一天修路100米,第二天比第一天多修20%。这个修路队第二天修路多少米
第 2 课时 求具体数量的问题
[解析] 把第一天修路长度看作单位“1”。
第 2 课时 求具体数量的问题
[答案]方法一:100×20%=20(米)
100+20=120(米)
方法二:100×(1+20%)= 120(米)
答:这个修路队第二天修路120 米。
■考点二 已知比一个数多(或少)百分之几的数是多少,求这个数
第 2 课时 求具体数量的问题
1.已知比一个数多(或少)百分之几的数是多少,求这个数的问题的特点是单位“1”的量未知。
2.解题方法:把单位“1"的量设为 x ,根据题中的等量关系列方程。
方法一:x×[1+(或-)另一个量比单位“1”的量多(或少)的百分率] =另一个量;
方法二:x +(或-)x×另一个量比单位“1”的量多(或少)的百分率=另一个量。
第 2 课时 求具体数量的问题
重难突破
单位“1”的量先增加再减少或先提高再降低相同的百分比,所得的量与单位“1”相等吗
答:不相等。单位“1”的量先增加再减少或先提高再降低相同的百分比,所得的量一定比单位“1”小。
例 2 小明家今年收西红柿800千克,收的西红柿比青椒多25%,收了多少千克青椒
第 2 课时 求具体数量的问题
[解析] 把收的青椒的质量看作单位“1”单位“1”的量是未知的,可以设为X。
根据“收的青椒的质量×(1+25%)=收的西红柿的质量”列方程求解。
第 2 课时 求具体数量的问题
[答案] 解:设收了x 千克青椒。
x ×(1+25%)=800
x=640
答:收了640 千克青椒。
第 2 课时 求具体数量的问题
■易错易混分析 找不准单位“1”导致列式错误
第 2 课时 求具体数量的问题
例 3 新丰电器公司去年创利税200万元,超过了原计划的25% ,原计划创利税多少万元
[解析] 在没有明显的“比”“是”或“占”等字眼时,要分析题意确定单位“1”,根据题意可知实际超过了原计划的25%,即实际的销售额与计划的相比,把原计划的销售额看作单位“1”,实际的销售额是原计划的1+25%= 125%。
第 2 课时 求具体数量的问题
[答案] 200÷(1+25%) =160(万元)
答:原计划创利税160万元。
易错警示 不能一眼确定出哪个量是单位“1”时,要结合题意仔细判断。
■考点 新闻中的百分数问题
第 3 课时 新闻中的百分数问题
解决已知比一个数多(或少)百分之几的数是多少的实际应用问题时,可以先找出单位“1”的量,再根据题干信息画出线段示意图,找出题目中的等量关系式,列方程进行解答。
例 1 2021年“十一”期间,某景区实现旅游门票收入1883.1万元,与上年同期相比增长了200%。2020年“十一”期间该景区旅游门票收入是多少万元
第 3 课时 新闻中的百分数问题
第 3 课时 新闻中的百分数问题
[解析] 把2020年“十一”期间该景区旅游门票收入看作单位“1”,设为x万元。
2020年“十一”期间该景区旅游门票收入+2020年“十一”期间该景区旅游门票收入×200%=2021年“十一”期间该景区旅游门票收入。
第 3 课时 新闻中的百分数问题
[答案]解:设2017年“十一”期间该景区旅游门票收入是x万元。
x+200%x=1883.1
x=627.7
答:2017年“十一”期间该景区旅游门票收入是627.7万元。
例 2 某地区2021年粮食作物种植面积为21万公顷,比上年减少10%。该地区2020年粮食作物的种植面积是多少万公顷 (得数保留一位小数)
第 3 课时 新闻中的百分数问题
[解析] 把2020年粮食作物的种植面积看作单位“1”,设为x万公顷。
该地区2020年粮食作物的种植面积-2020年粮食作物种植面积×10%=2021年粮食作物种植面积。
第 3 课时 新闻中的百分数问题
[答案] 解:设该地区2020年粮食作物的种植面积是 x 万公顷。
x-10%x=21
x≈23.3
答:该地区2020年粮食作物的种植面积是23.3万公顷。
第 3 课时 新闻中的百分数问题
(冀教版·六年级·上册)
5.1一般应用问题
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
一般应用问题
求一个数比另一个数多(或少)百分之几的问题:两个数的差量+单位“1”。
已知比一个数多(或少)百分之几的数是多少,求这个数的问题:可以列方程解答。
求比一个数多(或少)百分之几的数是多少的问题:单位“1"x[1+(或-)百分率]=另一个量。
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
折扣
几折就是百分之几十,几几折就是百分之几十几,这里的“几”都是大写的。
解决折扣问题时,先把折扣改写成百分数,与百分数应用题的解题思路和解题方法相同。
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
储蓄
存入银行的钱叫做本金;到期取款时银行多支付的钱叫做利息;利息与本金的比率叫做年利率。
利息=本金×年利率×存期。
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
成数
几成就是百分之几十,几成几就是百分之几十几,这里的“几”都是大写的。
解决成数问题时,先把成数改写成百分数,与百分数应用题的解题思路和解题方法相同。
第 1 课时 求一个数比另一个数多(或少)百分之几
百分数的应用
税收
税收是国家财政收入的主要来源,我国现行的主要税种有增值税、消费税和个人所得税等。
应纳税额=各种收入中应纳税部分×税率。
应纳税额与各种收入中应纳税部分的比率叫做税率。
■考点 求一个数比另-个数多(或少)百分之几
第 1 课时 求一个数比另一个数多(或少)百分之几
1.求一个数比另一个数多(或少)百分之几,实际上也是求一个数是另一个数的百分之几,即两个数的差量占另一个数(即单位“1”的量)的百分之几。
2.用甲表示一个数,用乙表示另一个数:
(1)求甲比乙多百分之儿的方法:(甲-乙)÷乙或甲÷乙-100%;
(2)求乙比甲少百分之几的方法:(甲-乙)÷甲或100%-乙÷甲。
第 1 课时 求一个数比另一个数多(或少)百分之几
3.在实际生活中,人们常用“增加百分之几”“减少百分之几”“节约百分之几”等来表示增加、减少的幅度。“增加百分之几”表示增加的是原来的百分之几,“减少百分之几”表示减少的是原来的百分之几,“节约百分之几”表示节约的是原来的百分之几。
第 1 课时 求一个数比另一个数多(或少)百分之几
重难突破
解决这类题的关键是什么
答:关键是找准单位“1”,一般“比”字后面是单位“1”的量,两个数的差就是比较量。用比较量作被除数,用单位“1”的量作除数。
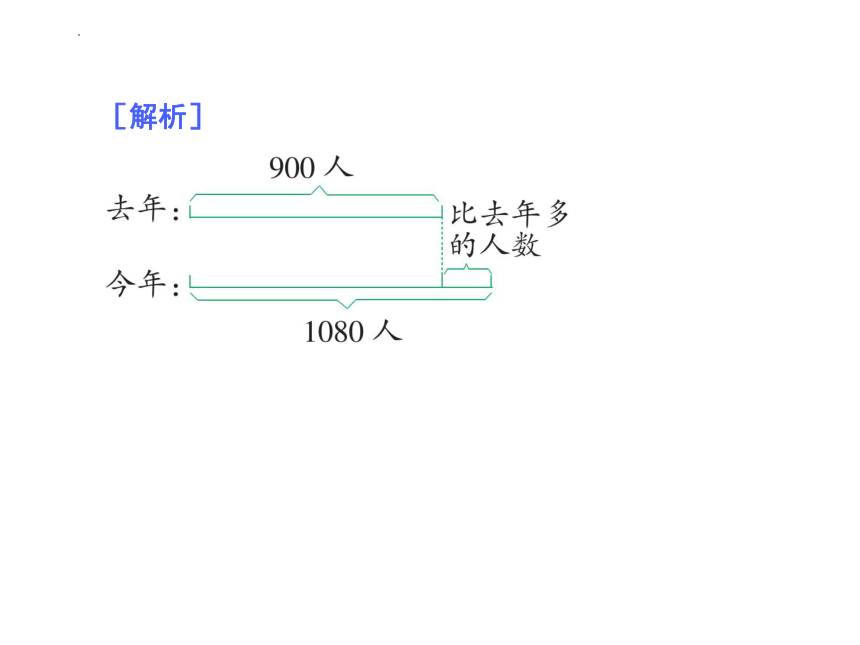
例 1 关西小学去年在校学生人数是900人,今年增加到了1080人。今年的在校学生人数比去年在校的人数增加了百分之几
第 1 课时 求一个数比另一个数多(或少)百分之几
[解析]
第 1 课时 求一个数比另一个数多(或少)百分之几
[答案] 方法一:(1080-900)÷900=20%
方法二:1080÷900=120%
120%-100%=20%
答:今年在校学生人数比去年在校的人数增加了20%。
第 1 课时 求一个数比另一个数多(或少)百分之几
例 2 一款笔记本电脑的原价是4000元,降价后的售价为3500元。现价比原价降低了百分之几
第 1 课时 求一个数比另一个数多(或少)百分之几
[解析]
[答案] 方法一:(4000-3500)÷4000=12.5%
方法二:1-3500÷4000=12.5%
答:现价比原价降低了12.5%。
第 1 课时 求一个数比另一个数多(或少)百分之几
■易错易混分析 没有找准单位“1”
第 1 课时 求一个数比另一个数多(或少)百分之几
例3 甲数:乙数=5:4,甲数比乙数多25%,那么乙数比甲数少( )%。
[解析]第一句中“比”字后面是乙数,把乙数看作单位“1”,甲数比乙数多(5-4)÷4=25%。求乙数比甲数少百分之几,是把甲数看作单位“1”,列式计算为(5-4)÷5=20%。
[答案] 20
易错警示:当存在两个单位“1”时,要根据不同的单位“1”进行分析,在不同的单位“1”下作比较,结果是不同的。
■考点一 求比一个数多(或少)百分之几的数是多少
第 2 课时 求具体数量的问题
1.求比一个数多(或少)百分之几的数是多少的问题的特点是单位“1”的量已知。
2.解题方法:方法一:单位“1”的量+(或-)单位“1”的量×另一个量比单位“1”的量多(或少)的百分率=另一个量;
方法二:单位“1”的量×[1+(或-)另一个量比单位“1”的量多(或少)的百分率] =另一个量。
3.“求比一个数多(或少)百分之几的数是多少”的问题的解法和“求比一个数多(或少)几分之几的数是多少”的解法相同,唯一的区别就是把几分之几变成了百分之几。
第 2 课时 求具体数量的问题
重难突破
解决这类问题应该注意什么
答:算出多(或少)的百分之几的数后要记得与原单位“1”相加(相减)。
例 1 一个修路队第一天修路100米,第二天比第一天多修20%。这个修路队第二天修路多少米
第 2 课时 求具体数量的问题
[解析] 把第一天修路长度看作单位“1”。
第 2 课时 求具体数量的问题
[答案]方法一:100×20%=20(米)
100+20=120(米)
方法二:100×(1+20%)= 120(米)
答:这个修路队第二天修路120 米。
■考点二 已知比一个数多(或少)百分之几的数是多少,求这个数
第 2 课时 求具体数量的问题
1.已知比一个数多(或少)百分之几的数是多少,求这个数的问题的特点是单位“1”的量未知。
2.解题方法:把单位“1"的量设为 x ,根据题中的等量关系列方程。
方法一:x×[1+(或-)另一个量比单位“1”的量多(或少)的百分率] =另一个量;
方法二:x +(或-)x×另一个量比单位“1”的量多(或少)的百分率=另一个量。
第 2 课时 求具体数量的问题
重难突破
单位“1”的量先增加再减少或先提高再降低相同的百分比,所得的量与单位“1”相等吗
答:不相等。单位“1”的量先增加再减少或先提高再降低相同的百分比,所得的量一定比单位“1”小。
例 2 小明家今年收西红柿800千克,收的西红柿比青椒多25%,收了多少千克青椒
第 2 课时 求具体数量的问题
[解析] 把收的青椒的质量看作单位“1”单位“1”的量是未知的,可以设为X。
根据“收的青椒的质量×(1+25%)=收的西红柿的质量”列方程求解。
第 2 课时 求具体数量的问题
[答案] 解:设收了x 千克青椒。
x ×(1+25%)=800
x=640
答:收了640 千克青椒。
第 2 课时 求具体数量的问题
■易错易混分析 找不准单位“1”导致列式错误
第 2 课时 求具体数量的问题
例 3 新丰电器公司去年创利税200万元,超过了原计划的25% ,原计划创利税多少万元
[解析] 在没有明显的“比”“是”或“占”等字眼时,要分析题意确定单位“1”,根据题意可知实际超过了原计划的25%,即实际的销售额与计划的相比,把原计划的销售额看作单位“1”,实际的销售额是原计划的1+25%= 125%。
第 2 课时 求具体数量的问题
[答案] 200÷(1+25%) =160(万元)
答:原计划创利税160万元。
易错警示 不能一眼确定出哪个量是单位“1”时,要结合题意仔细判断。
■考点 新闻中的百分数问题
第 3 课时 新闻中的百分数问题
解决已知比一个数多(或少)百分之几的数是多少的实际应用问题时,可以先找出单位“1”的量,再根据题干信息画出线段示意图,找出题目中的等量关系式,列方程进行解答。
例 1 2021年“十一”期间,某景区实现旅游门票收入1883.1万元,与上年同期相比增长了200%。2020年“十一”期间该景区旅游门票收入是多少万元
第 3 课时 新闻中的百分数问题
第 3 课时 新闻中的百分数问题
[解析] 把2020年“十一”期间该景区旅游门票收入看作单位“1”,设为x万元。
2020年“十一”期间该景区旅游门票收入+2020年“十一”期间该景区旅游门票收入×200%=2021年“十一”期间该景区旅游门票收入。
第 3 课时 新闻中的百分数问题
[答案]解:设2017年“十一”期间该景区旅游门票收入是x万元。
x+200%x=1883.1
x=627.7
答:2017年“十一”期间该景区旅游门票收入是627.7万元。
例 2 某地区2021年粮食作物种植面积为21万公顷,比上年减少10%。该地区2020年粮食作物的种植面积是多少万公顷 (得数保留一位小数)
第 3 课时 新闻中的百分数问题
[解析] 把2020年粮食作物的种植面积看作单位“1”,设为x万公顷。
该地区2020年粮食作物的种植面积-2020年粮食作物种植面积×10%=2021年粮食作物种植面积。
第 3 课时 新闻中的百分数问题
[答案] 解:设该地区2020年粮食作物的种植面积是 x 万公顷。
x-10%x=21
x≈23.3
答:该地区2020年粮食作物的种植面积是23.3万公顷。
第 3 课时 新闻中的百分数问题
