冀教版六年级上册数学4.2 圆的面积 课件(共31张PPT)
文档属性
| 名称 | 冀教版六年级上册数学4.2 圆的面积 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 380.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 15:16:16 | ||
图片预览










文档简介
(共31张PPT)
(冀教版·六年级·上册)
4.2圆的面积
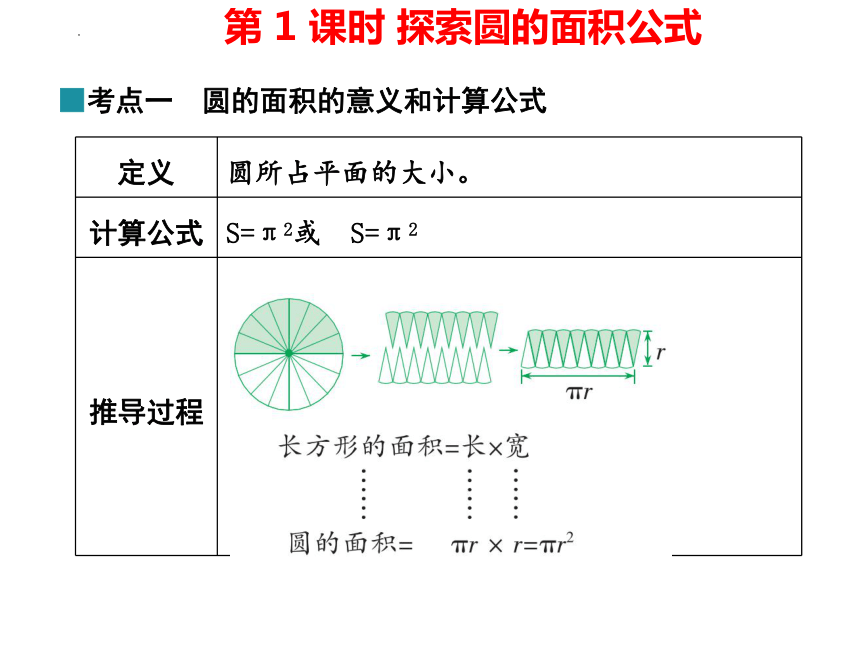
■考点一 圆的面积的意义和计算公式
第 1 课时 探索圆的面积公式
定义 圆所占平面的大小。
计算公式 S=π2或 S=π2
推导过程
第 1 课时 探索圆的面积公式
重难突破
推导圆的面积计算公式的过程中,所拼成的长方形的长和宽与圆的周长、半径有什么关系
答:长方形的长近似于圆周长的一半(πr),长方形的宽近似于圆的半径(r)。
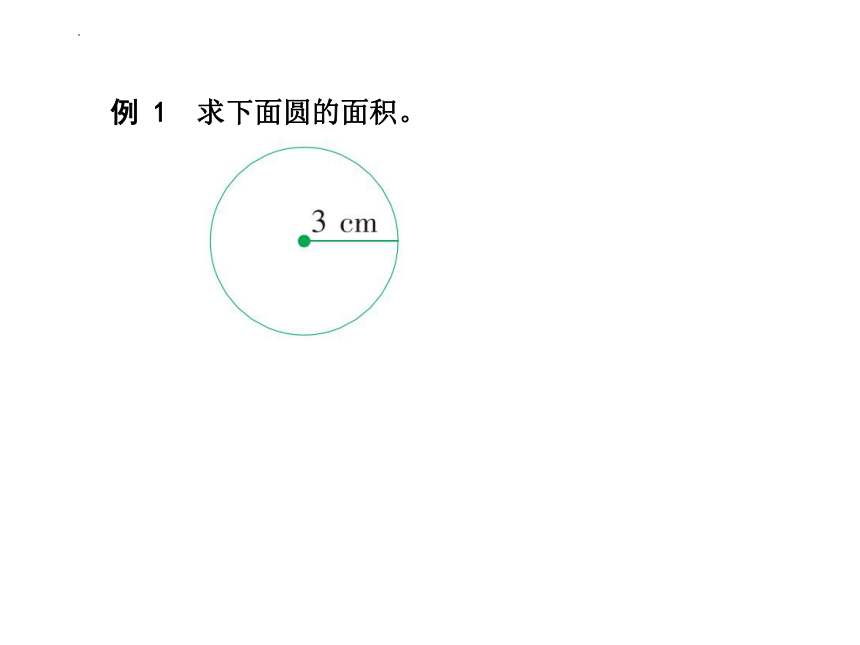
例 1 求下面圆的面积。
第 1 课时 探索圆的面积公式
[解析]利用公式S=πr2 直接计算即可。
[答案]3.14×32 =28.26(平方厘米)
第 1 课时 探索圆的面积公式
■考点二 圆的面积公式的应用
第 1 课时 探索圆的面积公式
已知圆的半径 r,根据S=πr2求圆的面积能解决生活中的一些问题 。
第 1 课时 探索圆的面积公式
重难突破
计算圆的面积的关键条件是什么
答:圆的面积公式是S=πr2,公式中只有r是未知数,因此关键是知道半径。
例 2 水上公园要建一所圆形的儿童水上游乐设施,规划半径为5米。要建的这所设施的占地面积是多少平方米
第 1 课时 探索圆的面积公式
[解析]占地面积即半径为5米的圆的面积。
圆的面积S=πr2
5米
[答案] 3.14×52=78.5(平方米)
答:要建的这所设施的占地面积是78.5平方米。
■易错易混分析 混淆了圆的周长和面积的意义
第 1 课时 探索圆的面积公式
例 3 学习了本节内容后,小明认为半径是2厘米的圆的周长和面积是相等的,他的想法对吗 为什么
[解析] 虽然半径是2厘米的圆的周长和面积的计算结果的数值都是12.56,是相等的,但圆的周长表示围成圆的曲线的长度,圆的面积表示圆所占平面的大小,所以不能作比较。
第 1 课时 探索圆的面积公式
[答案] 不对,因为周长和面积的意义不同,不能作比较。
易错警示 不能只关注题目中结果数据的大小而忽略了圆的周长和面积的意义不同,两者无法作比较。
■考点 已知直径求圆的面积
第 2 课时 已知直径求面积
已知圆的直径求圆的面积,需要先根据同圆中直径与半径的关系求出圆的半径,再求面积,S=π×2 。
第 2 课时 已知直径求面积
重难突破
圆的面积会随直径的扩大或缩小而发生怎样的变化
答:如果一个圆的直径扩大到原来的几倍,那么面积扩大到原来的几的平方倍。如果一个圆的直径缩小到原来的几分之一,那么面积就缩小到原来的几的平方分之一。
例 1 “神舟五号”飞船预先设定的降落范围是直径为20千米的圆,这个降落范围有多大
第 2 课时 已知直径求面积
[解析]这个降落范围是直径为20千米的圆的面积。利用公式S=π×2 计算,其中d=20千米。
[答案]3.14×2 =314(平方千米)
答:这个降落范围有314平方千米。
第 2 课时 已知直径求面积
■易错易混分析 误把直径当作半径代入S=πr2 求面积
第 2 课时 已知直径求面积
例 2 在一张边长是2分米的正方形彩纸上剪下一个最大的圆。这个圆形彩纸的面积是多少平方分米
[解析] 从正方形上剪最大的圆,圆的直径与正方形的边长相等,因此圆形彩纸的直径为2分米,半径为2÷2=1(分米),面积为3.14×12=3.14(平方分米)。
第 2 课时 已知直径求面积
[答案] 3.14×(2÷2)2=3.14(平方分米)
答:这个圆形彩纸的面积是3.14平方分米。
易错警示 根据给出的条件求圆形面积时,一定要看清是半径还是直径。
■考点一 已知周长求圆的面积
第 3 课时 已知周长求面积
已知圆的周长求圆的面积,需要先根据r =C÷π÷2求出圆的半径,再求面积。
第 3 课时 已知周长求面积
重难突破
“圆的周长越大,其面积就越大”说法正确吗
答:正确。圆的周长越大,其半径就越大根据圆的面积公式S=πr2可知,半径越大,面积就越大。
例 1 李奶奶用长25.12 米的篱笆围了块圆形菜地,这块菜地的面积是多少平方米
第 3 课时 已知周长求面积
[解析]篱笆长即圆形菜地的周长。
[答案] 25.12÷3.14÷2=4(米)
3.14×42=50.24(平方米)
答:这块菜地的面积是50.24平方米。
第 3 课时 已知周长求面积
■考点二 选择合适的台布
第 3 课时 已知周长求面积
例 2 一张圆桌的桌面直径是15分米,现在有边长分别是13分米、15分米和17分米的三块不同规格的正方形台布,选哪一共合适明2为什么
[解析]先分别求出桌面和三块台布的面积,再逐一分析能不能符合实际使用的要求。
[答案] 桌面面积:
3.14×2 =176.625(平方分米)
第一块台布的面积:13×13=169(平方分米)
第二块台布的面积:15×15=225(平方分米)
第三块台布的面积:17×17=289(平方分米)
第一块台布的面积小于桌面的面积,不合适,第二块台布的边长和圆桌的直径相等,刚刚能盖住桌面,不合适,第三块台布不仅能盖住桌面,而且周围均能下垂,所以选边长为17分米的台布最合适。
第 3 课时 已知周长求面积
■考点 圆环的认识及其面积
第 4 课时 圆环的面积
1.如下图中,阴影部分为圆环。
圆环中较大的圆叫外圆,外圆半径用R表示;较小的圆叫内圆,内圆半径用r表示。两个圆之间的宽度叫做环宽,环宽=外圆半径-内圆半径。
第 4 课时 圆环的面积
2.圆环面积:用外圆的面积减去内圆的面积就可以求出圆环的面积。即S=πR2-πr2,也可以写成S=π(R2-r2)。
第 4 课时 圆环的面积
重难突破
圆环有什么特点
答:(1)构成圆环的两个圆是半径不相等的同心圆。(2)圆环是轴对称图形,它有无数条对称轴。通过圆心的直线都是它的对称轴。
例 1 一个圆环形铁片,内圆直径是4厘米,环宽是1厘米。这个铁片的面积是多少平方厘米
第 4 课时 圆环的面积
[解析]
[答案] 3.14×[(4÷2+1)2- (4÷2)2]=15.7(平方厘米)
答:这个铁片的面积是15.7 平方厘米。
第 4 课时 圆环的面积
例 2 求下面阴影部分的面积。
第 4 课时 圆环的面积
[解析] S阴影=S圆环+2=π(R2 - r2)÷2
4+2=6(厘米) 4厘米
[答案] 3.14×[(4+2)2- 42]÷2=31.4(平方厘米)
第 4 课时 圆环的面积
■易错易混分析 误将环宽当成内圆半径计算圆环面积
第 4 课时 圆环的面积
例 3 公园里有一个圆形花坛的直径是8米,在这个花坛周围修了一条宽2米的小路,你能计算出小路的面积是多少平方米吗
3.14×[(8÷2)2-22]=37.68(平方米)
上面的列式正确吗 若不对, 请改正。
[解析]求修建的小路的面积,就是求圆环的面积,圆环内圆半径为8÷2=4(米),外圓半径为4+2=6(米),再利用圓环面积公式求解即可。
[答案] 不对。改正:8÷2=4(米)
4+2=6(米) 3.14×(62-42)=62.8(平方米)
第 4 课时 圆环的面积
易错警示 路宽是圆环的环宽,不是内圆的半径。
(冀教版·六年级·上册)
4.2圆的面积
■考点一 圆的面积的意义和计算公式
第 1 课时 探索圆的面积公式
定义 圆所占平面的大小。
计算公式 S=π2或 S=π2
推导过程
第 1 课时 探索圆的面积公式
重难突破
推导圆的面积计算公式的过程中,所拼成的长方形的长和宽与圆的周长、半径有什么关系
答:长方形的长近似于圆周长的一半(πr),长方形的宽近似于圆的半径(r)。
例 1 求下面圆的面积。
第 1 课时 探索圆的面积公式
[解析]利用公式S=πr2 直接计算即可。
[答案]3.14×32 =28.26(平方厘米)
第 1 课时 探索圆的面积公式
■考点二 圆的面积公式的应用
第 1 课时 探索圆的面积公式
已知圆的半径 r,根据S=πr2求圆的面积能解决生活中的一些问题 。
第 1 课时 探索圆的面积公式
重难突破
计算圆的面积的关键条件是什么
答:圆的面积公式是S=πr2,公式中只有r是未知数,因此关键是知道半径。
例 2 水上公园要建一所圆形的儿童水上游乐设施,规划半径为5米。要建的这所设施的占地面积是多少平方米
第 1 课时 探索圆的面积公式
[解析]占地面积即半径为5米的圆的面积。
圆的面积S=πr2
5米
[答案] 3.14×52=78.5(平方米)
答:要建的这所设施的占地面积是78.5平方米。
■易错易混分析 混淆了圆的周长和面积的意义
第 1 课时 探索圆的面积公式
例 3 学习了本节内容后,小明认为半径是2厘米的圆的周长和面积是相等的,他的想法对吗 为什么
[解析] 虽然半径是2厘米的圆的周长和面积的计算结果的数值都是12.56,是相等的,但圆的周长表示围成圆的曲线的长度,圆的面积表示圆所占平面的大小,所以不能作比较。
第 1 课时 探索圆的面积公式
[答案] 不对,因为周长和面积的意义不同,不能作比较。
易错警示 不能只关注题目中结果数据的大小而忽略了圆的周长和面积的意义不同,两者无法作比较。
■考点 已知直径求圆的面积
第 2 课时 已知直径求面积
已知圆的直径求圆的面积,需要先根据同圆中直径与半径的关系求出圆的半径,再求面积,S=π×2 。
第 2 课时 已知直径求面积
重难突破
圆的面积会随直径的扩大或缩小而发生怎样的变化
答:如果一个圆的直径扩大到原来的几倍,那么面积扩大到原来的几的平方倍。如果一个圆的直径缩小到原来的几分之一,那么面积就缩小到原来的几的平方分之一。
例 1 “神舟五号”飞船预先设定的降落范围是直径为20千米的圆,这个降落范围有多大
第 2 课时 已知直径求面积
[解析]这个降落范围是直径为20千米的圆的面积。利用公式S=π×2 计算,其中d=20千米。
[答案]3.14×2 =314(平方千米)
答:这个降落范围有314平方千米。
第 2 课时 已知直径求面积
■易错易混分析 误把直径当作半径代入S=πr2 求面积
第 2 课时 已知直径求面积
例 2 在一张边长是2分米的正方形彩纸上剪下一个最大的圆。这个圆形彩纸的面积是多少平方分米
[解析] 从正方形上剪最大的圆,圆的直径与正方形的边长相等,因此圆形彩纸的直径为2分米,半径为2÷2=1(分米),面积为3.14×12=3.14(平方分米)。
第 2 课时 已知直径求面积
[答案] 3.14×(2÷2)2=3.14(平方分米)
答:这个圆形彩纸的面积是3.14平方分米。
易错警示 根据给出的条件求圆形面积时,一定要看清是半径还是直径。
■考点一 已知周长求圆的面积
第 3 课时 已知周长求面积
已知圆的周长求圆的面积,需要先根据r =C÷π÷2求出圆的半径,再求面积。
第 3 课时 已知周长求面积
重难突破
“圆的周长越大,其面积就越大”说法正确吗
答:正确。圆的周长越大,其半径就越大根据圆的面积公式S=πr2可知,半径越大,面积就越大。
例 1 李奶奶用长25.12 米的篱笆围了块圆形菜地,这块菜地的面积是多少平方米
第 3 课时 已知周长求面积
[解析]篱笆长即圆形菜地的周长。
[答案] 25.12÷3.14÷2=4(米)
3.14×42=50.24(平方米)
答:这块菜地的面积是50.24平方米。
第 3 课时 已知周长求面积
■考点二 选择合适的台布
第 3 课时 已知周长求面积
例 2 一张圆桌的桌面直径是15分米,现在有边长分别是13分米、15分米和17分米的三块不同规格的正方形台布,选哪一共合适明2为什么
[解析]先分别求出桌面和三块台布的面积,再逐一分析能不能符合实际使用的要求。
[答案] 桌面面积:
3.14×2 =176.625(平方分米)
第一块台布的面积:13×13=169(平方分米)
第二块台布的面积:15×15=225(平方分米)
第三块台布的面积:17×17=289(平方分米)
第一块台布的面积小于桌面的面积,不合适,第二块台布的边长和圆桌的直径相等,刚刚能盖住桌面,不合适,第三块台布不仅能盖住桌面,而且周围均能下垂,所以选边长为17分米的台布最合适。
第 3 课时 已知周长求面积
■考点 圆环的认识及其面积
第 4 课时 圆环的面积
1.如下图中,阴影部分为圆环。
圆环中较大的圆叫外圆,外圆半径用R表示;较小的圆叫内圆,内圆半径用r表示。两个圆之间的宽度叫做环宽,环宽=外圆半径-内圆半径。
第 4 课时 圆环的面积
2.圆环面积:用外圆的面积减去内圆的面积就可以求出圆环的面积。即S=πR2-πr2,也可以写成S=π(R2-r2)。
第 4 课时 圆环的面积
重难突破
圆环有什么特点
答:(1)构成圆环的两个圆是半径不相等的同心圆。(2)圆环是轴对称图形,它有无数条对称轴。通过圆心的直线都是它的对称轴。
例 1 一个圆环形铁片,内圆直径是4厘米,环宽是1厘米。这个铁片的面积是多少平方厘米
第 4 课时 圆环的面积
[解析]
[答案] 3.14×[(4÷2+1)2- (4÷2)2]=15.7(平方厘米)
答:这个铁片的面积是15.7 平方厘米。
第 4 课时 圆环的面积
例 2 求下面阴影部分的面积。
第 4 课时 圆环的面积
[解析] S阴影=S圆环+2=π(R2 - r2)÷2
4+2=6(厘米) 4厘米
[答案] 3.14×[(4+2)2- 42]÷2=31.4(平方厘米)
第 4 课时 圆环的面积
■易错易混分析 误将环宽当成内圆半径计算圆环面积
第 4 课时 圆环的面积
例 3 公园里有一个圆形花坛的直径是8米,在这个花坛周围修了一条宽2米的小路,你能计算出小路的面积是多少平方米吗
3.14×[(8÷2)2-22]=37.68(平方米)
上面的列式正确吗 若不对, 请改正。
[解析]求修建的小路的面积,就是求圆环的面积,圆环内圆半径为8÷2=4(米),外圓半径为4+2=6(米),再利用圓环面积公式求解即可。
[答案] 不对。改正:8÷2=4(米)
4+2=6(米) 3.14×(62-42)=62.8(平方米)
第 4 课时 圆环的面积
易错警示 路宽是圆环的环宽,不是内圆的半径。
