2025浙江高考物理一轮复习-“17~20解答”限时练15(含解析)
文档属性
| 名称 | 2025浙江高考物理一轮复习-“17~20解答”限时练15(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 119.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-02 20:02:40 | ||
图片预览


文档简介
2025浙江高考物理一轮复习-“17~20解答”限时练15
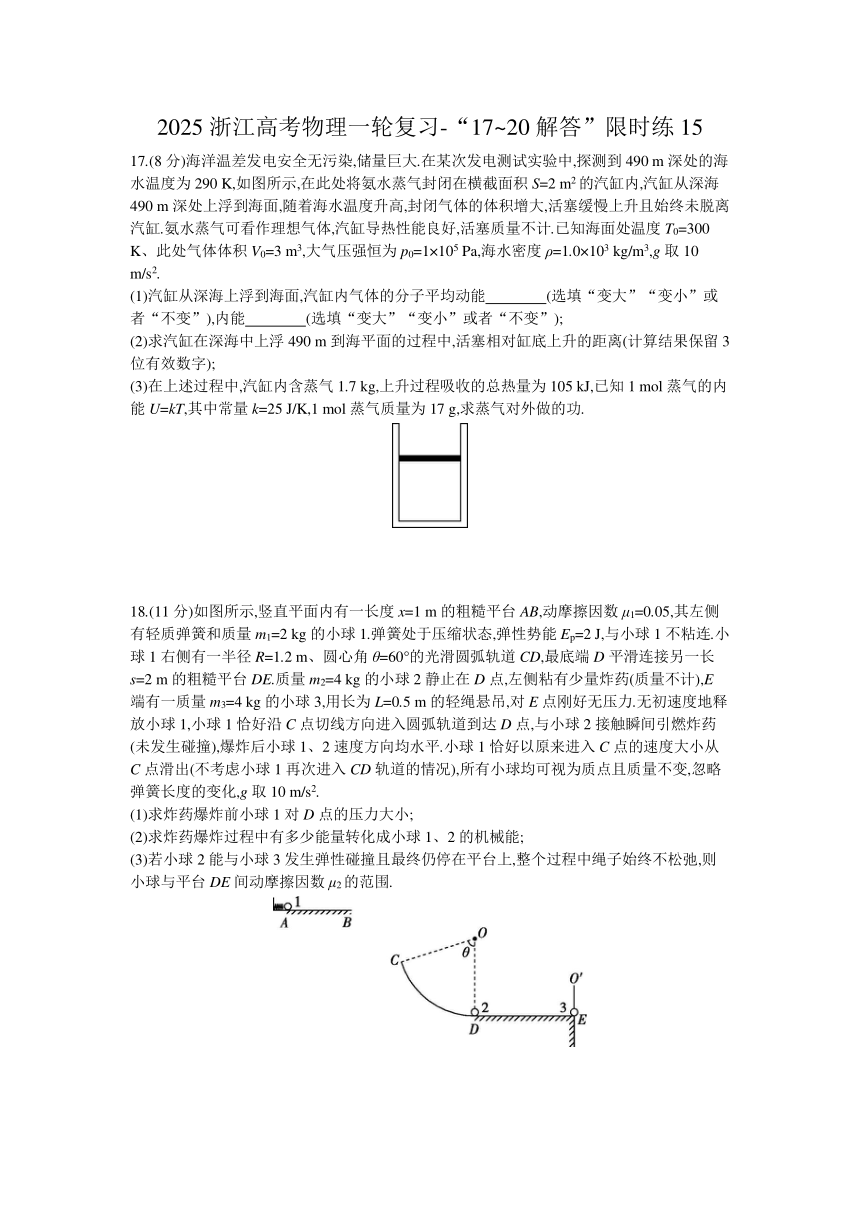
17.(8分)海洋温差发电安全无污染,储量巨大.在某次发电测试实验中,探测到490 m深处的海水温度为290 K,如图所示,在此处将氨水蒸气封闭在横截面积S=2 m2的汽缸内,汽缸从深海490 m深处上浮到海面,随着海水温度升高,封闭气体的体积增大,活塞缓慢上升且始终未脱离汽缸.氨水蒸气可看作理想气体,汽缸导热性能良好,活塞质量不计.已知海面处温度T0=300 K、此处气体体积V0=3 m3,大气压强恒为p0=1×105 Pa,海水密度ρ=1.0×103 kg/m3,g取10 m/s2.
(1)汽缸从深海上浮到海面,汽缸内气体的分子平均动能 (选填“变大”“变小”或者“不变”),内能 (选填“变大”“变小”或者“不变”);
(2)求汽缸在深海中上浮490 m到海平面的过程中,活塞相对缸底上升的距离(计算结果保留3位有效数字);
(3)在上述过程中,汽缸内含蒸气1.7 kg,上升过程吸收的总热量为105 kJ,已知1 mol蒸气的内能U=kT,其中常量k=25 J/K,1 mol蒸气质量为17 g,求蒸气对外做的功.
18.(11分)如图所示,竖直平面内有一长度x=1 m的粗糙平台AB,动摩擦因数μ1=0.05,其左侧有轻质弹簧和质量m1=2 kg的小球1.弹簧处于压缩状态,弹性势能Ep=2 J,与小球1不粘连.小球1右侧有一半径R=1.2 m、圆心角θ=60°的光滑圆弧轨道CD,最底端D平滑连接另一长s=2 m的粗糙平台DE.质量m2=4 kg的小球2静止在D点,左侧粘有少量炸药(质量不计),E端有一质量m3=4 kg的小球3,用长为L=0.5 m的轻绳悬吊,对E点刚好无压力.无初速度地释放小球1,小球1恰好沿C点切线方向进入圆弧轨道到达D点,与小球2接触瞬间引燃炸药(未发生碰撞),爆炸后小球1、2速度方向均水平.小球1恰好以原来进入C点的速度大小从C点滑出(不考虑小球1再次进入CD轨道的情况),所有小球均可视为质点且质量不变,忽略弹簧长度的变化,g取10 m/s2.
(1)求炸药爆炸前小球1对D点的压力大小;
(2)求炸药爆炸过程中有多少能量转化成小球1、2的机械能;
(3)若小球2能与小球3发生弹性碰撞且最终仍停在平台上,整个过程中绳子始终不松弛,则小球与平台DE间动摩擦因数μ2的范围.
19.(11分)某中学兴趣小组研究了电机系统的工作原理,认识到电机系统可实现驱动和阻尼,设计了如图所示装置.电阻不计的“L形”金属导轨由足够长竖直部分和水平部分连接构成,竖直导轨间存在水平向右的匀强磁场,磁感应强度大小为B.导体棒ab与竖直导轨始终接触良好并通过轻质滑轮连接重物M,初始ab被锁定不动.已知导体棒ab的质量为m,重物M质量为3m,竖直导轨间距为d.电源电动势E=,内阻为R,导体棒与定值电阻阻值均为R.
(1)把开关K接1,解除导体棒锁定,导体棒经时间t恰好开始匀速上升,求:
①通过导体棒的电流方向;
②导体棒匀速上升时的速度;
③此过程导体棒上升的高度h;
(2)把开关K接2,解除导体棒锁定,导体棒经时间t'、下落高度h'时恰好开始匀速下落,求此过程中回路产生的总焦耳热.
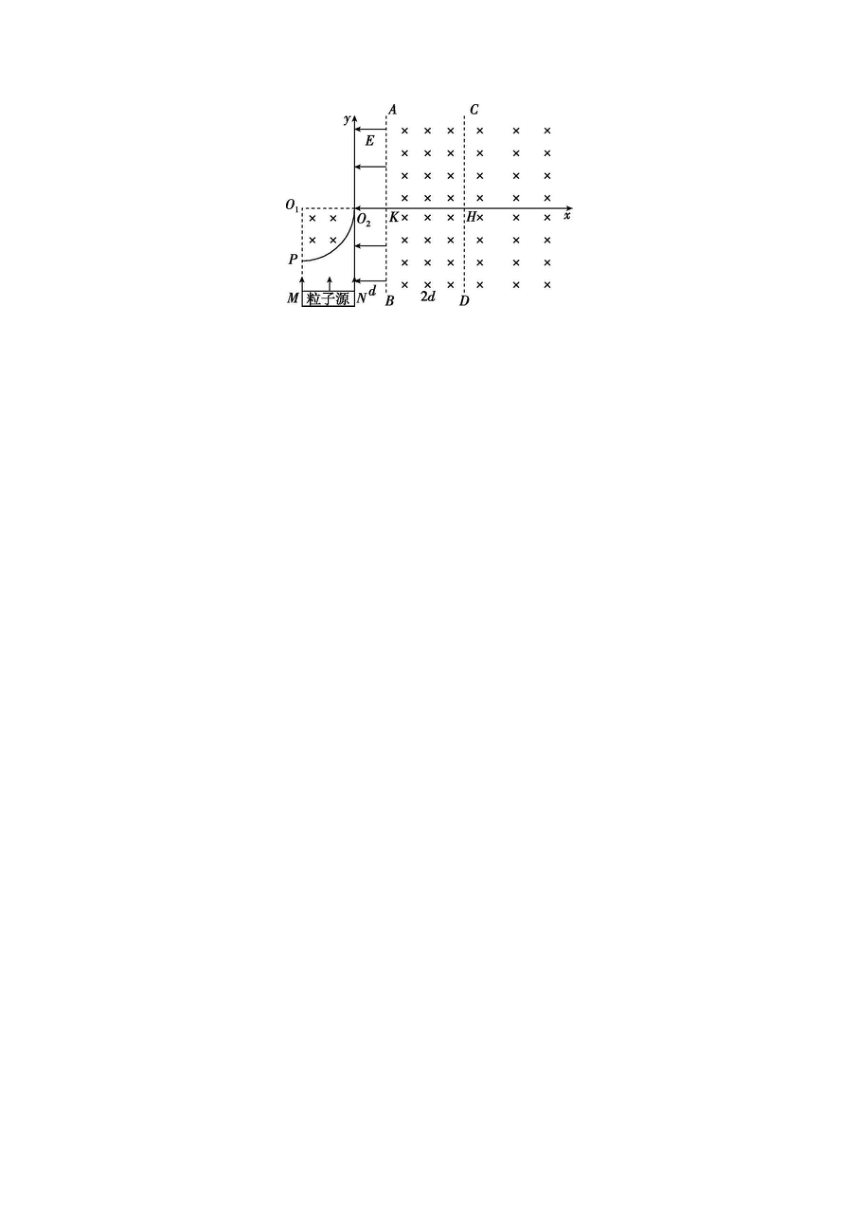
20.(11分)[2024·衢州模拟] 磁共振成像(MRI)利用带电粒子在强磁场中的运动来生成图像.通过对被检体施加强磁场,并在其周围施加梯度磁场,可以得到不同组织的信号,从而生成高分辨率的内部结构图像.现有如下情景:在平面内有如图所示的垂直纸面向里、半径为d的四分之一圆形匀强磁场,磁感应强度为B0,圆心O1在x轴上,O2为直角坐标系原点;y轴右侧有宽度为d、方向沿x轴负向的匀强电场,AB右侧存在宽度为2d、磁感应强度也为B0,方向垂直纸面向里的匀强磁场;CD右侧存在沿x轴正方向线性递增的梯度磁场,磁感应强度满足B=kx'B0(x'为点到CD的距离),在y轴方向磁感应强度大小相同,磁场范围足够大.有一平行于x轴的宽度为d的线状粒子源MN(N在y轴上)源源不断发射沿y轴正方向初速度相同的带负电粒子(电荷量大小为q、质量为m),从M点出发进入四分之一圆形匀强磁场的粒子恰好从O2点进入电场,电场强度大小为.不考虑各场的边缘效应,不计粒子重力.求:
(1)粒子的初速度v0;
(2)粒子穿过AB边界时的速率v;
(3)粒子在AB、CD间的磁场区域内运动的最短时间;
(4)所有粒子运动过程能达到的横坐标(x轴)的最大值是多少.
参考答案与详细解析
17.(1)变大 变大 (2)1.47 m
(3)80 kJ
[解析] (1)汽缸从深海上浮到海面,海水温度升高,气体的温度升高,则分子平均动能变大,内能变大 (2分)
(2)初始时压强p1=p0+ρgh=5×106 Pa(1分)
根据理想气体状态方程= (1分)
解得V1=0.058 m3
V0-V1=ΔhS
解得Δh=1.47 m(1分)
(3)根据热力学第一定律有
ΔU=W+Q (1分)
ΔU=kΔT=25 kJ(1分)
解得W=-80 kJ
即对外做功80 kJ(1分)
18.(1) N (2)32 J
(3)0.15≤μ2<0.4
[解析] (1)小球1从A运动到B点,根据能量守恒定律有Ep-μ1m1gx=m1 (1分)
解得vB=1 m/s
小球1从B到C做平抛运动,则有vC==2 m/s
小球1从C到D,根据机械能守恒定律有
m1+m1gR(1-cos 60°)=m1 (1分)
解得vD=4 m/s
小球1在D点,根据牛顿第二定律有FN-m1g=m1 (1分)
解得FN= N
根据牛顿第三定律可知小球1对轨道的压力大小为 N(1分)
(2)炸药爆炸过程中,根据动量守恒定律有
m1vD=-m1vD'+m2v (1分)
其中vD'=vD=4 m/s
则机械能的增加量为ΔE=m1vD'2+m2v2-m1 (1分)
解得ΔE=32 J,v=4 m/s(1分)
(3)①当小球2刚好运动到小球3处时速度为零,则有
-μ2m2gs=0-m2v2 (1分)
解得μ2=0.4
②设小球2运动到小球3处的速度为v2'(此时未与小球3碰撞),则有-μ2m2gs=m2v2'2-m2v2 (1分)
之后小球2与小球3发生弹性碰撞,由于两球的质量相等,则速度交换,故碰撞后小球3的速度为v3=v2',为保证整个过程中绳子始终不松弛,且最终小球2仍停在平台上,则小球3最多运动到右侧圆心O'等高处,则有
m3=m3gL (1分)
联立解得μ2=0.15
当μ2=0.15时,小球3从圆心O'等高处回到最低点与小球2再次相碰后,又交换速度,可计算出小球2不会从左侧轨道C处飞出,最终会停在平台上
综上所述可知0.15≤μ2<0.4(1分)
19.(1)①方向由a到b ② ③ (2)-2mgh'
[解析] (1)①导体棒向上运动,根据右手定则,电流方向由a到b (1分)
②设导体棒以速度v1匀速上升,感应电流为I= (1分)
由平衡得BId+mg=3mg (1分)
得v1= (1分)
③根据动量定理有t-Bdq=4mv1 (1分)
电荷量为q=Δt=Δt=
得h= (1分)
(2)开关K接2,导体棒匀速运动时的电流为
I'= (1分)
由平衡得BI'd=3mg-mg (1分)
得v2=
根据动量定理有Bdq'-t'=4mv2 (1分)
得q'=+
由能量守恒有Eq'=×4m+h'+Q (1分)
得Q=10t'+-2mgh'(1分)
20.(1) (2) (3) (4)3d+
[解析] (1)由题可知粒子做圆周运动的轨道半径为d,由匀速圆周运动洛伦兹力提供圆周运动的向心力可知d=
解得v0= (2分)
(2)由题可知Eqd=mv2-m(1分)
解得v=2v0= (1分)
(3)在AB、CD间的磁场区域内R==2d (1分)
圆周运动弦长最短为2d,圆心角为,分析可知当粒子从N点出发时符合条件,轨迹如图所示
T= (1分)
t== (1分)
(4)对运动粒子y轴方向动量定理,在x轴方向最远时速度方向为y轴负方向,有
(1分)
qB02d+qkB0=mv+mv0(1分)
x'=
坐标值为3d+ (2分)
17.(8分)海洋温差发电安全无污染,储量巨大.在某次发电测试实验中,探测到490 m深处的海水温度为290 K,如图所示,在此处将氨水蒸气封闭在横截面积S=2 m2的汽缸内,汽缸从深海490 m深处上浮到海面,随着海水温度升高,封闭气体的体积增大,活塞缓慢上升且始终未脱离汽缸.氨水蒸气可看作理想气体,汽缸导热性能良好,活塞质量不计.已知海面处温度T0=300 K、此处气体体积V0=3 m3,大气压强恒为p0=1×105 Pa,海水密度ρ=1.0×103 kg/m3,g取10 m/s2.
(1)汽缸从深海上浮到海面,汽缸内气体的分子平均动能 (选填“变大”“变小”或者“不变”),内能 (选填“变大”“变小”或者“不变”);
(2)求汽缸在深海中上浮490 m到海平面的过程中,活塞相对缸底上升的距离(计算结果保留3位有效数字);
(3)在上述过程中,汽缸内含蒸气1.7 kg,上升过程吸收的总热量为105 kJ,已知1 mol蒸气的内能U=kT,其中常量k=25 J/K,1 mol蒸气质量为17 g,求蒸气对外做的功.
18.(11分)如图所示,竖直平面内有一长度x=1 m的粗糙平台AB,动摩擦因数μ1=0.05,其左侧有轻质弹簧和质量m1=2 kg的小球1.弹簧处于压缩状态,弹性势能Ep=2 J,与小球1不粘连.小球1右侧有一半径R=1.2 m、圆心角θ=60°的光滑圆弧轨道CD,最底端D平滑连接另一长s=2 m的粗糙平台DE.质量m2=4 kg的小球2静止在D点,左侧粘有少量炸药(质量不计),E端有一质量m3=4 kg的小球3,用长为L=0.5 m的轻绳悬吊,对E点刚好无压力.无初速度地释放小球1,小球1恰好沿C点切线方向进入圆弧轨道到达D点,与小球2接触瞬间引燃炸药(未发生碰撞),爆炸后小球1、2速度方向均水平.小球1恰好以原来进入C点的速度大小从C点滑出(不考虑小球1再次进入CD轨道的情况),所有小球均可视为质点且质量不变,忽略弹簧长度的变化,g取10 m/s2.
(1)求炸药爆炸前小球1对D点的压力大小;
(2)求炸药爆炸过程中有多少能量转化成小球1、2的机械能;
(3)若小球2能与小球3发生弹性碰撞且最终仍停在平台上,整个过程中绳子始终不松弛,则小球与平台DE间动摩擦因数μ2的范围.
19.(11分)某中学兴趣小组研究了电机系统的工作原理,认识到电机系统可实现驱动和阻尼,设计了如图所示装置.电阻不计的“L形”金属导轨由足够长竖直部分和水平部分连接构成,竖直导轨间存在水平向右的匀强磁场,磁感应强度大小为B.导体棒ab与竖直导轨始终接触良好并通过轻质滑轮连接重物M,初始ab被锁定不动.已知导体棒ab的质量为m,重物M质量为3m,竖直导轨间距为d.电源电动势E=,内阻为R,导体棒与定值电阻阻值均为R.
(1)把开关K接1,解除导体棒锁定,导体棒经时间t恰好开始匀速上升,求:
①通过导体棒的电流方向;
②导体棒匀速上升时的速度;
③此过程导体棒上升的高度h;
(2)把开关K接2,解除导体棒锁定,导体棒经时间t'、下落高度h'时恰好开始匀速下落,求此过程中回路产生的总焦耳热.
20.(11分)[2024·衢州模拟] 磁共振成像(MRI)利用带电粒子在强磁场中的运动来生成图像.通过对被检体施加强磁场,并在其周围施加梯度磁场,可以得到不同组织的信号,从而生成高分辨率的内部结构图像.现有如下情景:在平面内有如图所示的垂直纸面向里、半径为d的四分之一圆形匀强磁场,磁感应强度为B0,圆心O1在x轴上,O2为直角坐标系原点;y轴右侧有宽度为d、方向沿x轴负向的匀强电场,AB右侧存在宽度为2d、磁感应强度也为B0,方向垂直纸面向里的匀强磁场;CD右侧存在沿x轴正方向线性递增的梯度磁场,磁感应强度满足B=kx'B0(x'为点到CD的距离),在y轴方向磁感应强度大小相同,磁场范围足够大.有一平行于x轴的宽度为d的线状粒子源MN(N在y轴上)源源不断发射沿y轴正方向初速度相同的带负电粒子(电荷量大小为q、质量为m),从M点出发进入四分之一圆形匀强磁场的粒子恰好从O2点进入电场,电场强度大小为.不考虑各场的边缘效应,不计粒子重力.求:
(1)粒子的初速度v0;
(2)粒子穿过AB边界时的速率v;
(3)粒子在AB、CD间的磁场区域内运动的最短时间;
(4)所有粒子运动过程能达到的横坐标(x轴)的最大值是多少.
参考答案与详细解析
17.(1)变大 变大 (2)1.47 m
(3)80 kJ
[解析] (1)汽缸从深海上浮到海面,海水温度升高,气体的温度升高,则分子平均动能变大,内能变大 (2分)
(2)初始时压强p1=p0+ρgh=5×106 Pa(1分)
根据理想气体状态方程= (1分)
解得V1=0.058 m3
V0-V1=ΔhS
解得Δh=1.47 m(1分)
(3)根据热力学第一定律有
ΔU=W+Q (1分)
ΔU=kΔT=25 kJ(1分)
解得W=-80 kJ
即对外做功80 kJ(1分)
18.(1) N (2)32 J
(3)0.15≤μ2<0.4
[解析] (1)小球1从A运动到B点,根据能量守恒定律有Ep-μ1m1gx=m1 (1分)
解得vB=1 m/s
小球1从B到C做平抛运动,则有vC==2 m/s
小球1从C到D,根据机械能守恒定律有
m1+m1gR(1-cos 60°)=m1 (1分)
解得vD=4 m/s
小球1在D点,根据牛顿第二定律有FN-m1g=m1 (1分)
解得FN= N
根据牛顿第三定律可知小球1对轨道的压力大小为 N(1分)
(2)炸药爆炸过程中,根据动量守恒定律有
m1vD=-m1vD'+m2v (1分)
其中vD'=vD=4 m/s
则机械能的增加量为ΔE=m1vD'2+m2v2-m1 (1分)
解得ΔE=32 J,v=4 m/s(1分)
(3)①当小球2刚好运动到小球3处时速度为零,则有
-μ2m2gs=0-m2v2 (1分)
解得μ2=0.4
②设小球2运动到小球3处的速度为v2'(此时未与小球3碰撞),则有-μ2m2gs=m2v2'2-m2v2 (1分)
之后小球2与小球3发生弹性碰撞,由于两球的质量相等,则速度交换,故碰撞后小球3的速度为v3=v2',为保证整个过程中绳子始终不松弛,且最终小球2仍停在平台上,则小球3最多运动到右侧圆心O'等高处,则有
m3=m3gL (1分)
联立解得μ2=0.15
当μ2=0.15时,小球3从圆心O'等高处回到最低点与小球2再次相碰后,又交换速度,可计算出小球2不会从左侧轨道C处飞出,最终会停在平台上
综上所述可知0.15≤μ2<0.4(1分)
19.(1)①方向由a到b ② ③ (2)-2mgh'
[解析] (1)①导体棒向上运动,根据右手定则,电流方向由a到b (1分)
②设导体棒以速度v1匀速上升,感应电流为I= (1分)
由平衡得BId+mg=3mg (1分)
得v1= (1分)
③根据动量定理有t-Bdq=4mv1 (1分)
电荷量为q=Δt=Δt=
得h= (1分)
(2)开关K接2,导体棒匀速运动时的电流为
I'= (1分)
由平衡得BI'd=3mg-mg (1分)
得v2=
根据动量定理有Bdq'-t'=4mv2 (1分)
得q'=+
由能量守恒有Eq'=×4m+h'+Q (1分)
得Q=10t'+-2mgh'(1分)
20.(1) (2) (3) (4)3d+
[解析] (1)由题可知粒子做圆周运动的轨道半径为d,由匀速圆周运动洛伦兹力提供圆周运动的向心力可知d=
解得v0= (2分)
(2)由题可知Eqd=mv2-m(1分)
解得v=2v0= (1分)
(3)在AB、CD间的磁场区域内R==2d (1分)
圆周运动弦长最短为2d,圆心角为,分析可知当粒子从N点出发时符合条件,轨迹如图所示
T= (1分)
t== (1分)
(4)对运动粒子y轴方向动量定理,在x轴方向最远时速度方向为y轴负方向,有
(1分)
qB02d+qkB0=mv+mv0(1分)
x'=
坐标值为3d+ (2分)
同课章节目录
