2025浙江高考物理一轮复习-“17~20解答”限时练16(含解析)
文档属性
| 名称 | 2025浙江高考物理一轮复习-“17~20解答”限时练16(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 118.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-02 00:00:00 | ||
图片预览



文档简介
2025浙江高考物理一轮复习-“17~20解答”限时练16
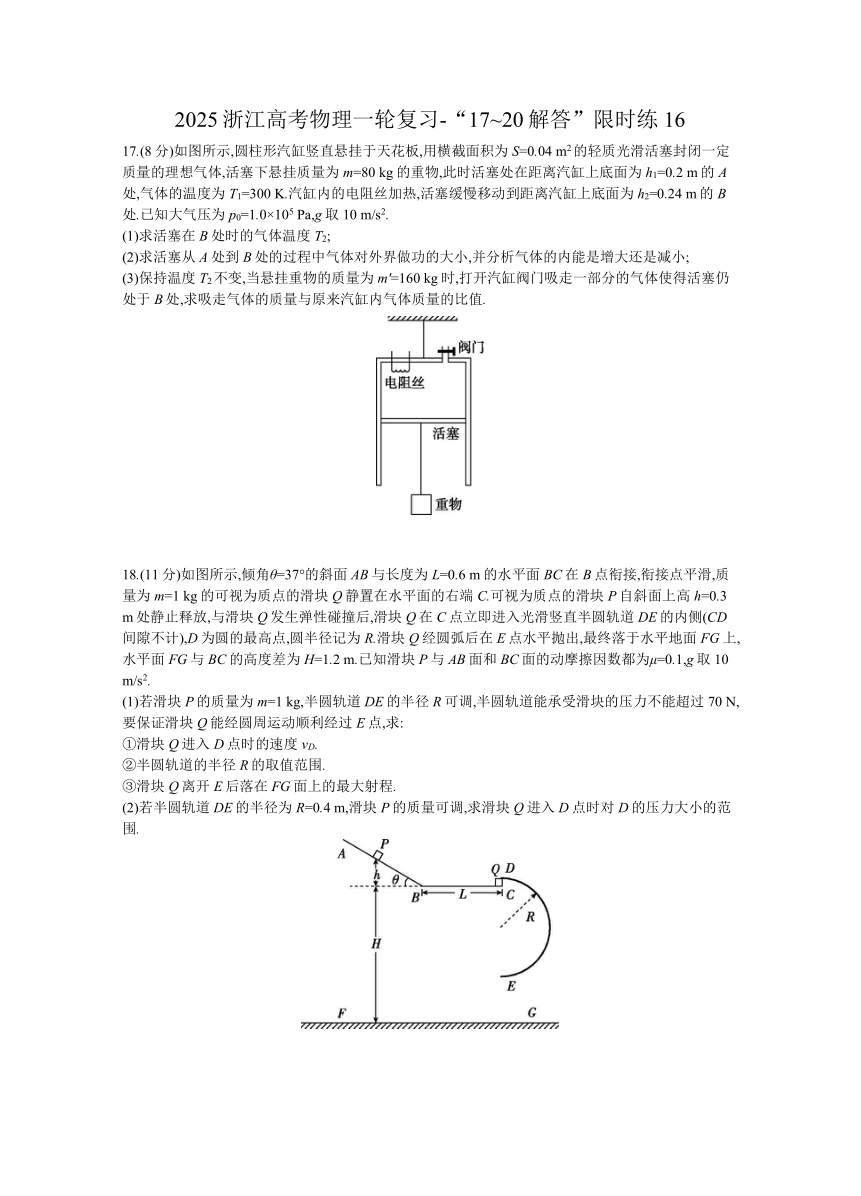
17.(8分)如图所示,圆柱形汽缸竖直悬挂于天花板,用横截面积为S=0.04 m2的轻质光滑活塞封闭一定质量的理想气体,活塞下悬挂质量为m=80 kg的重物,此时活塞处在距离汽缸上底面为h1=0.2 m的A处,气体的温度为T1=300 K.汽缸内的电阻丝加热,活塞缓慢移动到距离汽缸上底面为h2=0.24 m的B处.已知大气压为p0=1.0×105 Pa,g取10 m/s2.
(1)求活塞在B处时的气体温度T2;
(2)求活塞从A处到B处的过程中气体对外界做功的大小,并分析气体的内能是增大还是减小;
(3)保持温度T2不变,当悬挂重物的质量为m'=160 kg时,打开汽缸阀门吸走一部分的气体使得活塞仍处于B处,求吸走气体的质量与原来汽缸内气体质量的比值.
18.(11分)如图所示,倾角θ=37°的斜面AB与长度为L=0.6 m的水平面BC在B点衔接,衔接点平滑,质量为m=1 kg的可视为质点的滑块Q静置在水平面的右端C.可视为质点的滑块P自斜面上高h=0.3 m处静止释放,与滑块Q发生弹性碰撞后,滑块Q在C点立即进入光滑竖直半圆轨道DE的内侧(CD间隙不计),D为圆的最高点,圆半径记为R.滑块Q经圆弧后在E点水平抛出,最终落于水平地面FG上,水平面FG与BC的高度差为H=1.2 m.已知滑块P与AB面和BC面的动摩擦因数都为μ=0.1,g取10 m/s2.
(1)若滑块P的质量为m=1 kg,半圆轨道DE的半径R可调,半圆轨道能承受滑块的压力不能超过70 N,要保证滑块Q能经圆周运动顺利经过E点,求:
①滑块Q进入D点时的速度vD.
②半圆轨道的半径R的取值范围.
③滑块Q离开E后落在FG面上的最大射程.
(2)若半圆轨道DE的半径为R=0.4 m,滑块P的质量可调,求滑块Q进入D点时对D的压力大小的范围.
19.(11分)水平放置的金属细圆环P的半径为l,其内部充满方向竖直向上的匀强磁场,磁感应强度大小为B.电阻为r,长度恰为l的细导体棒a一端搭接在细圆环上,可绕圆心处的金属细圆柱O在水平面内转动.两平行竖直金属导轨的间距为d,其中M导轨与小圆柱O相连,N导轨与圆环P相连,两导轨上方通过开关K连接能提供恒定电流大小为I、方向水平向右的恒流源S.质量为m、电阻为R的均匀导体棒b水平搁置在固定支架上并与两导轨紧密接触,棒b处在方向垂直于导轨平面向内的匀强磁场中,磁感应强度的大小为B.除了导体棒a和导体棒b外其余电阻不计,一切摩擦不计.
(1)若开关K断开,外力使导体棒a以某一角速度ω匀速转动时导体棒b对支架的作用力恰好为0,求此时导体棒a的旋转方向(俯视图)和ω的大小.
(2)若开关K闭合,导体棒a作为“电动机”在水平面内旋转.
①“电动机”空载时导体棒a所受安培力为零,其匀速转动的角速度记为ω0,求ω0的大小.
②求“电动机”机械效率为50%时导体棒a的角速度ω2.
20.(11分)空腔圆柱的截面圆如图所示,其圆心为O,半径为R,圆面上开有A、B、C、D四个小孔,∠AOB=90°,∠BOC=120°,∠COD=90°,圆内存在垂直纸面向外的匀强磁场,磁感应强度大小B1未知,圆外OB和OC射线范围内存在垂直纸面向内的匀强磁场,磁感应强度大小B2未知.紧靠A孔有两金属板M、N,两板间加上交变电压UMN=U0sin ,其中U0已知,质量为m、电荷量为q的带正电粒子持续由M板静止释放,经电场加速的粒子从A孔沿半径方向进入空腔内部,发现在t=时刻释放的粒子恰好能从B孔射出磁场,并能经过D孔.已知粒子在电场中加速的时间忽略不计,粒子撞击圆面即被吸收,圆面始终不带电.
(1)求从B孔飞出的粒子的速度v0及截面圆内磁感应强度B1的大小;
(2)求粒子从A孔运动到D孔的时间T'及比值B1∶B2;
(3)紧靠D孔有两金属板M'、N',两板间加上沿半径方向的交变电压UM'N'=sin -,以N'板出口处O'点为原点建立直角坐标系xO'y,在y轴右侧0≤x≤x0区域内存在垂直纸面向内的匀强磁场,磁感应强度为B3,当x0=2 cm时,从O'点进入磁场的速度最大的粒子恰好从点P离开磁场.若要让从O'点进入磁场的速度最小的粒子也恰好击中点P,则x0的取值应为多少
参考答案与详细解析
17.(1)360 K (2)128 J 增大 (3)
[解析] (1)A到B为等压过程,根据盖-吕萨克定律有
= (1分)
即=
得T2=360 K(1分)
(2)设气体压强为p,由活塞受力平衡有
mg+pS=p0S (1分)
得p=8×104 Pa
气体对外界做功
W=pS=128 J(1分)
理想气体的分子势能忽略不计,而温度升高则分子动能增加,内能由分子势能和分子动能组成,所以气体内能增大. (1分)
(3)由(2)可知气体初状态压强为
p2=p=8×104 Pa,V2=h2S (1分)
悬挂质量为m'的重物后由活塞受力平衡有m'g+p3S=p0S
得压强p3=6×104 Pa
若不打开阀门,气体体积变为V3=h3S
该等温过程有p2h2S=p3h3S (1分)
得h3=0.32 m
吸走气体的质量与原来汽缸内气体质量的比值
== (1分)
18.(1)①2 m/s ②0.2 m≤R≤0.4 m ③1.4 m (2)0≤FN<30 N
[解析] (1)①滑块P从静止到C点,根据动能定理有
mgh-μmg-μmgL=m (1分)
解得vC=2 m/s
滑块P与滑块Q碰撞时动量守恒,有
mvC=mvC'+mvD (1分)
又因为是弹性碰撞,则机械能守恒
m=mvC'2+m
解得vD=2 m/s(1分)
②在D点能够做圆周运动,根据牛顿第二定律可知
mg≤m (1分)
解得R≤0.4 m
D点到E点的过程,根据能量守恒定律有
m-m=2mgR (1分)
在E点,根据牛顿第二定律有
FN-mg=m (1分)
且FN≤70N
联立得R≥0.2 m
所以R的取值范围为
0.2 m≤R≤0.4 m(1分)
③自E点做平抛运动,则射程为
x=vEt,H-2R=gt2 (1分)
将②中vE代入得
x=
分析可知当R=0.25 m时,解得xmax=1.4 m(1分)
(2)设P质量为m1,由动能定理有
m1gh-μm1g-μm1gL=m1
解得vC=2 m/s
滑块P与滑块Q碰撞时动量守恒,则
m1vC=m1v1+mv2
又因为是弹性碰撞,根据能量守恒定律有
m1=m1+m
解得v2=vC
即v2=vC
则0由牛顿第二定律有FN+mg=m
解得0≤FN<30 N(1分)
19.(1)顺时针方向旋转 (2)① ②
[解析] (1)导体棒b平衡,有mg=BI1d (1分)
电流I1=
电动势E=Bl2ω (1分)
联立得ω= (1分)
由左手定则和右手定则得导体棒a顺时针方向旋转 (1分)
(2)①空载时导体棒a所受安培力为零,则导体棒a的电流为零,导体棒a与导体棒b两端电压相等,导体棒b的电流即恒流源电流I,有
Bl2ω0=IR (1分)
所以ω0= (1分)
②法一:设导体棒a切割的电动势为E,其电流为i
导体棒a与导体棒b两端电压相等,即
(I-i)R=Bl2ω2+ir (1分)
由于导体棒a上的速度随着到圆心距离均匀增大,电动机功率
P机=F安 (1分)
P机=Bil= (1分)
η===50%(1分)
解得ω2= (1分)
法二:设导体棒a切割的电动势为E,其电流为i
导体棒a与导体棒b两端电压相等,即 (1分)
R=Bl2ω2+ir (2分)
η===50%(1分)
解得ω2= (1分)
20.(1)
(2)πR
(3)0.8 cm
[解析] (1)t=时刻的电压为UMN=
粒子在电场中加速,有qUMN=m
得v0= (1分)
由几何关系得,从A到B的过程中的轨迹半径为R,由
qv0B1=m
联立解得B1= (1分)
(2)由(1)得,速度为v0的粒子才能经过B孔,进而经过C孔和D孔,由几何关系得,从B孔到C孔的轨迹的圆心角为π,半径为r=Rtan =R (1分)
从C孔到D孔的轨迹的圆心角为,半径为R,则
T'= (1分)
解得T'=πR (1分)
由=
得= (1分)
(3)在t=+nT时刻和t=+nT时刻进入A孔的粒子能经过B孔,则粒子经过D孔的时刻为t=+nT+T'和t=+nT+T',设t=+nT+T'时刻经过N'板后的速度为v1,则
q-q=m (1分)
设t=+nT+T'时刻经过N'板后的速度为v2,则
q+q=m (1分)
得=
由题意得最大圆半径r2=2 cm
则最小圆半径r1=1 cm
r1圆轨迹方程为
x2+(y-1)2=1
设粒子自点Q(x0,y0)离开轨迹圆沿切线飞出,由几何关系得
= (1分)
同时满足
+(y0-1)2=1 (1分)
联立得x0=0.8 cm(1分)
17.(8分)如图所示,圆柱形汽缸竖直悬挂于天花板,用横截面积为S=0.04 m2的轻质光滑活塞封闭一定质量的理想气体,活塞下悬挂质量为m=80 kg的重物,此时活塞处在距离汽缸上底面为h1=0.2 m的A处,气体的温度为T1=300 K.汽缸内的电阻丝加热,活塞缓慢移动到距离汽缸上底面为h2=0.24 m的B处.已知大气压为p0=1.0×105 Pa,g取10 m/s2.
(1)求活塞在B处时的气体温度T2;
(2)求活塞从A处到B处的过程中气体对外界做功的大小,并分析气体的内能是增大还是减小;
(3)保持温度T2不变,当悬挂重物的质量为m'=160 kg时,打开汽缸阀门吸走一部分的气体使得活塞仍处于B处,求吸走气体的质量与原来汽缸内气体质量的比值.
18.(11分)如图所示,倾角θ=37°的斜面AB与长度为L=0.6 m的水平面BC在B点衔接,衔接点平滑,质量为m=1 kg的可视为质点的滑块Q静置在水平面的右端C.可视为质点的滑块P自斜面上高h=0.3 m处静止释放,与滑块Q发生弹性碰撞后,滑块Q在C点立即进入光滑竖直半圆轨道DE的内侧(CD间隙不计),D为圆的最高点,圆半径记为R.滑块Q经圆弧后在E点水平抛出,最终落于水平地面FG上,水平面FG与BC的高度差为H=1.2 m.已知滑块P与AB面和BC面的动摩擦因数都为μ=0.1,g取10 m/s2.
(1)若滑块P的质量为m=1 kg,半圆轨道DE的半径R可调,半圆轨道能承受滑块的压力不能超过70 N,要保证滑块Q能经圆周运动顺利经过E点,求:
①滑块Q进入D点时的速度vD.
②半圆轨道的半径R的取值范围.
③滑块Q离开E后落在FG面上的最大射程.
(2)若半圆轨道DE的半径为R=0.4 m,滑块P的质量可调,求滑块Q进入D点时对D的压力大小的范围.
19.(11分)水平放置的金属细圆环P的半径为l,其内部充满方向竖直向上的匀强磁场,磁感应强度大小为B.电阻为r,长度恰为l的细导体棒a一端搭接在细圆环上,可绕圆心处的金属细圆柱O在水平面内转动.两平行竖直金属导轨的间距为d,其中M导轨与小圆柱O相连,N导轨与圆环P相连,两导轨上方通过开关K连接能提供恒定电流大小为I、方向水平向右的恒流源S.质量为m、电阻为R的均匀导体棒b水平搁置在固定支架上并与两导轨紧密接触,棒b处在方向垂直于导轨平面向内的匀强磁场中,磁感应强度的大小为B.除了导体棒a和导体棒b外其余电阻不计,一切摩擦不计.
(1)若开关K断开,外力使导体棒a以某一角速度ω匀速转动时导体棒b对支架的作用力恰好为0,求此时导体棒a的旋转方向(俯视图)和ω的大小.
(2)若开关K闭合,导体棒a作为“电动机”在水平面内旋转.
①“电动机”空载时导体棒a所受安培力为零,其匀速转动的角速度记为ω0,求ω0的大小.
②求“电动机”机械效率为50%时导体棒a的角速度ω2.
20.(11分)空腔圆柱的截面圆如图所示,其圆心为O,半径为R,圆面上开有A、B、C、D四个小孔,∠AOB=90°,∠BOC=120°,∠COD=90°,圆内存在垂直纸面向外的匀强磁场,磁感应强度大小B1未知,圆外OB和OC射线范围内存在垂直纸面向内的匀强磁场,磁感应强度大小B2未知.紧靠A孔有两金属板M、N,两板间加上交变电压UMN=U0sin ,其中U0已知,质量为m、电荷量为q的带正电粒子持续由M板静止释放,经电场加速的粒子从A孔沿半径方向进入空腔内部,发现在t=时刻释放的粒子恰好能从B孔射出磁场,并能经过D孔.已知粒子在电场中加速的时间忽略不计,粒子撞击圆面即被吸收,圆面始终不带电.
(1)求从B孔飞出的粒子的速度v0及截面圆内磁感应强度B1的大小;
(2)求粒子从A孔运动到D孔的时间T'及比值B1∶B2;
(3)紧靠D孔有两金属板M'、N',两板间加上沿半径方向的交变电压UM'N'=sin -,以N'板出口处O'点为原点建立直角坐标系xO'y,在y轴右侧0≤x≤x0区域内存在垂直纸面向内的匀强磁场,磁感应强度为B3,当x0=2 cm时,从O'点进入磁场的速度最大的粒子恰好从点P离开磁场.若要让从O'点进入磁场的速度最小的粒子也恰好击中点P,则x0的取值应为多少
参考答案与详细解析
17.(1)360 K (2)128 J 增大 (3)
[解析] (1)A到B为等压过程,根据盖-吕萨克定律有
= (1分)
即=
得T2=360 K(1分)
(2)设气体压强为p,由活塞受力平衡有
mg+pS=p0S (1分)
得p=8×104 Pa
气体对外界做功
W=pS=128 J(1分)
理想气体的分子势能忽略不计,而温度升高则分子动能增加,内能由分子势能和分子动能组成,所以气体内能增大. (1分)
(3)由(2)可知气体初状态压强为
p2=p=8×104 Pa,V2=h2S (1分)
悬挂质量为m'的重物后由活塞受力平衡有m'g+p3S=p0S
得压强p3=6×104 Pa
若不打开阀门,气体体积变为V3=h3S
该等温过程有p2h2S=p3h3S (1分)
得h3=0.32 m
吸走气体的质量与原来汽缸内气体质量的比值
== (1分)
18.(1)①2 m/s ②0.2 m≤R≤0.4 m ③1.4 m (2)0≤FN<30 N
[解析] (1)①滑块P从静止到C点,根据动能定理有
mgh-μmg-μmgL=m (1分)
解得vC=2 m/s
滑块P与滑块Q碰撞时动量守恒,有
mvC=mvC'+mvD (1分)
又因为是弹性碰撞,则机械能守恒
m=mvC'2+m
解得vD=2 m/s(1分)
②在D点能够做圆周运动,根据牛顿第二定律可知
mg≤m (1分)
解得R≤0.4 m
D点到E点的过程,根据能量守恒定律有
m-m=2mgR (1分)
在E点,根据牛顿第二定律有
FN-mg=m (1分)
且FN≤70N
联立得R≥0.2 m
所以R的取值范围为
0.2 m≤R≤0.4 m(1分)
③自E点做平抛运动,则射程为
x=vEt,H-2R=gt2 (1分)
将②中vE代入得
x=
分析可知当R=0.25 m时,解得xmax=1.4 m(1分)
(2)设P质量为m1,由动能定理有
m1gh-μm1g-μm1gL=m1
解得vC=2 m/s
滑块P与滑块Q碰撞时动量守恒,则
m1vC=m1v1+mv2
又因为是弹性碰撞,根据能量守恒定律有
m1=m1+m
解得v2=vC
即v2=vC
则0
解得0≤FN<30 N(1分)
19.(1)顺时针方向旋转 (2)① ②
[解析] (1)导体棒b平衡,有mg=BI1d (1分)
电流I1=
电动势E=Bl2ω (1分)
联立得ω= (1分)
由左手定则和右手定则得导体棒a顺时针方向旋转 (1分)
(2)①空载时导体棒a所受安培力为零,则导体棒a的电流为零,导体棒a与导体棒b两端电压相等,导体棒b的电流即恒流源电流I,有
Bl2ω0=IR (1分)
所以ω0= (1分)
②法一:设导体棒a切割的电动势为E,其电流为i
导体棒a与导体棒b两端电压相等,即
(I-i)R=Bl2ω2+ir (1分)
由于导体棒a上的速度随着到圆心距离均匀增大,电动机功率
P机=F安 (1分)
P机=Bil= (1分)
η===50%(1分)
解得ω2= (1分)
法二:设导体棒a切割的电动势为E,其电流为i
导体棒a与导体棒b两端电压相等,即 (1分)
R=Bl2ω2+ir (2分)
η===50%(1分)
解得ω2= (1分)
20.(1)
(2)πR
(3)0.8 cm
[解析] (1)t=时刻的电压为UMN=
粒子在电场中加速,有qUMN=m
得v0= (1分)
由几何关系得,从A到B的过程中的轨迹半径为R,由
qv0B1=m
联立解得B1= (1分)
(2)由(1)得,速度为v0的粒子才能经过B孔,进而经过C孔和D孔,由几何关系得,从B孔到C孔的轨迹的圆心角为π,半径为r=Rtan =R (1分)
从C孔到D孔的轨迹的圆心角为,半径为R,则
T'= (1分)
解得T'=πR (1分)
由=
得= (1分)
(3)在t=+nT时刻和t=+nT时刻进入A孔的粒子能经过B孔,则粒子经过D孔的时刻为t=+nT+T'和t=+nT+T',设t=+nT+T'时刻经过N'板后的速度为v1,则
q-q=m (1分)
设t=+nT+T'时刻经过N'板后的速度为v2,则
q+q=m (1分)
得=
由题意得最大圆半径r2=2 cm
则最小圆半径r1=1 cm
r1圆轨迹方程为
x2+(y-1)2=1
设粒子自点Q(x0,y0)离开轨迹圆沿切线飞出,由几何关系得
= (1分)
同时满足
+(y0-1)2=1 (1分)
联立得x0=0.8 cm(1分)
同课章节目录
