第九章 平面直角坐标系(配优)综合题(含答案)
文档属性
| 名称 | 第九章 平面直角坐标系(配优)综合题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 443.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 18:52:11 | ||
图片预览

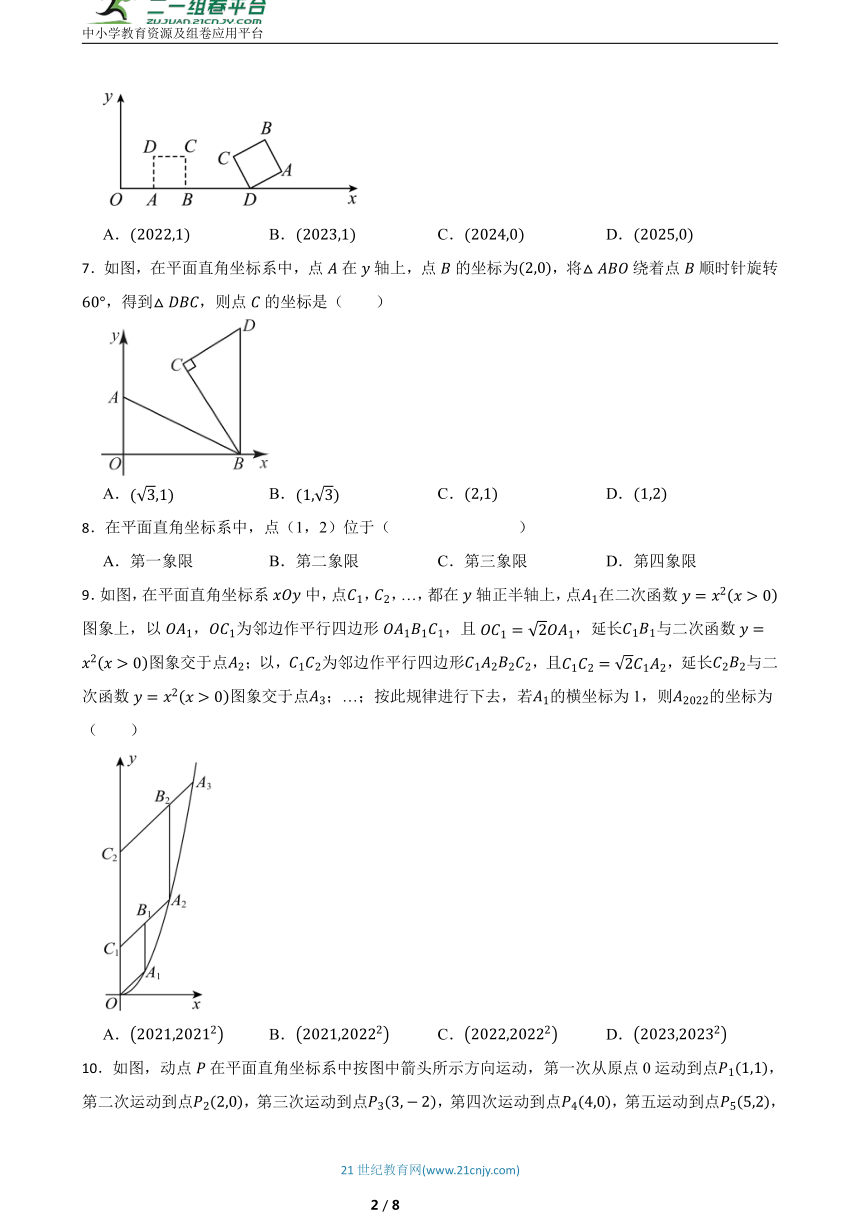
文档简介
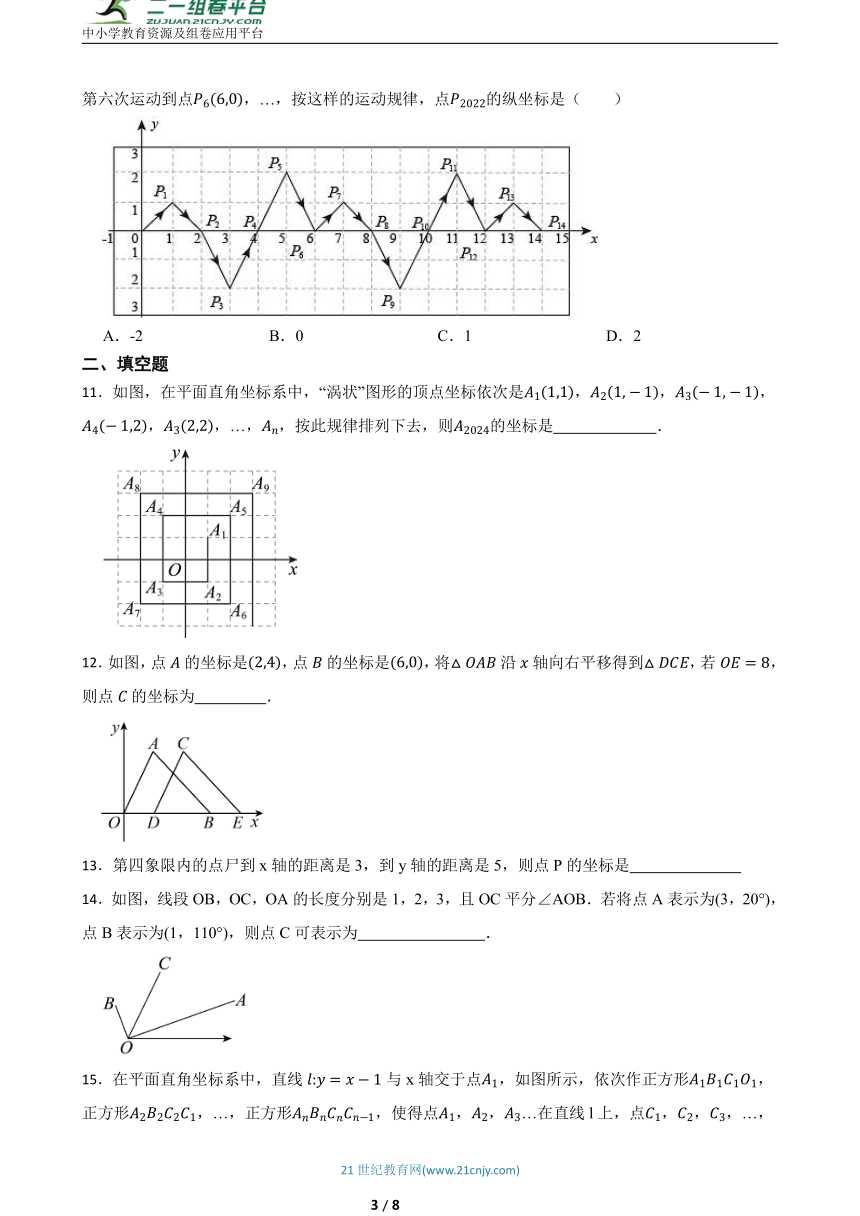
中小学教育资源及组卷应用平台
第九章 平面直角坐标系(配优)综合题
一、单选题
1.如图,将绕点O逆时针旋转90°,得到.若点的坐标为,则点A的坐标为( )
A. B. C. D.
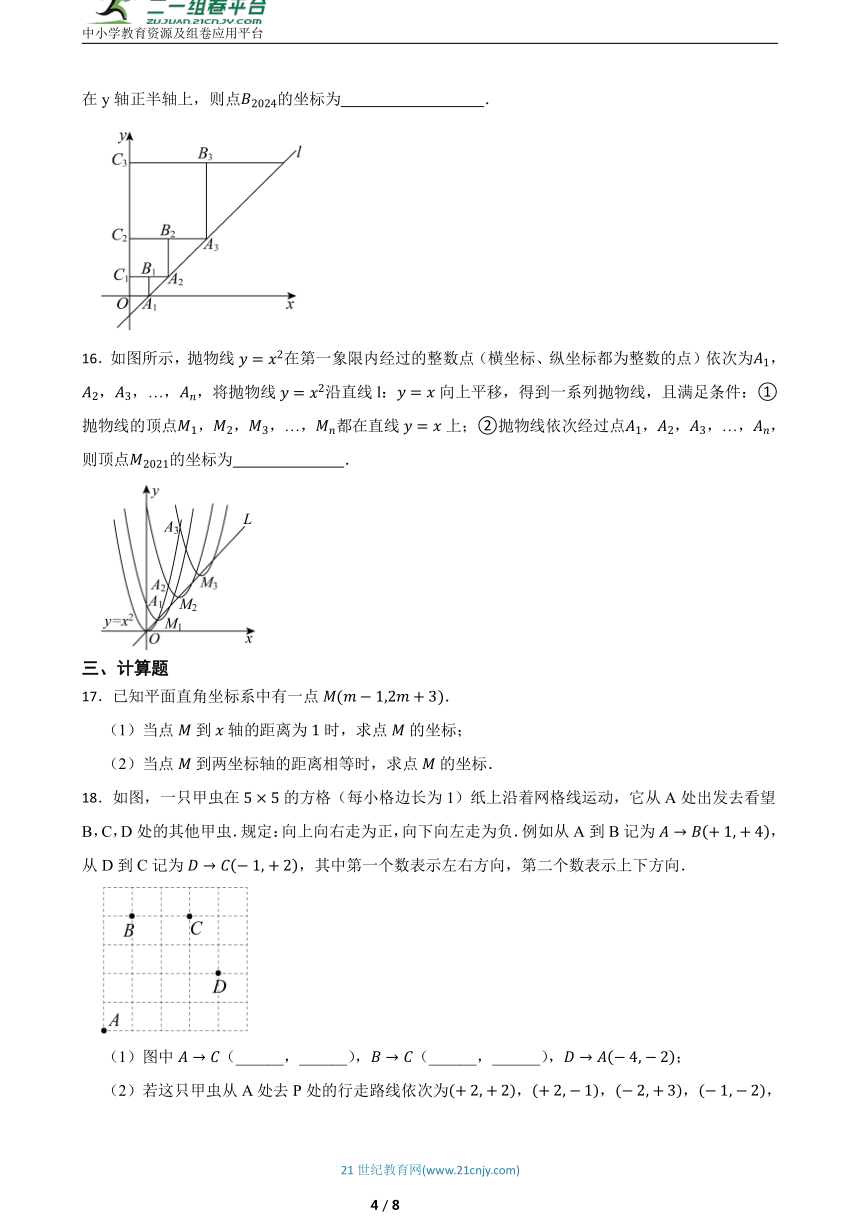
2.如图所示,若在象棋盘上建立直角坐标系,使“将”位于点,“象”位于点,则“炮”位于点( )
A. B. C. D.
3.在平面直角坐标系中,点到轴的距离是( )
A.1 B.2 C.4 D.6
4.如图,在象棋棋盘上建立平面直角坐标系,使“马”位于点,“兵”位于点,则“帅”所在位置的坐标是( )
A. B. C. D.
5.在平面直角坐标系中,点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图,在平面直角坐标系中,是边长为个单位长度的小正方形的顶点,开始时,顶点依次放在点的位置,然后向右滚动,第次滚动使点落在点的位置,第次滚动使点落在点的位置,…,按此规律滚动下去,则第次滚动后,顶点的坐标是( )
A. B. C. D.
7.如图,在平面直角坐标系中,点在轴上,点的坐标为,将绕着点顺时针旋转,得到,则点的坐标是( )
A. B. C. D.
8.在平面直角坐标系中,点(1,2)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图,在平面直角坐标系中,点,,…,都在轴正半轴上,点在二次函数图象上,以,为邻边作平行四边形,且,延长与二次函数图象交于点;以,为邻边作平行四边形,且,延长与二次函数图象交于点;…;按此规律进行下去,若的横坐标为1,则的坐标为( )
A. B. C. D.
10.如图,动点在平面直角坐标系中按图中箭头所示方向运动,第一次从原点0运动到点,第二次运动到点,第三次运动到点,第四次运动到点,第五运动到点,第六次运动到点,…,按这样的运动规律,点的纵坐标是( )
A.-2 B.0 C.1 D.2
二、填空题
11.如图,在平面直角坐标系中,“涡状”图形的顶点坐标依次是,,,,,…,,按此规律排列下去,则的坐标是 .
12.如图,点的坐标是,点的坐标是,将沿轴向右平移得到,若,则点的坐标为 .
13.第四象限内的点尸到x轴的距离是3,到y轴的距离是5,则点P的坐标是
14.如图,线段OB,OC,OA的长度分别是1,2,3,且OC平分∠AOB.若将点A表示为(3,20°),点B表示为(1,110°),则点C可表示为 .
15.在平面直角坐标系中,直线与x轴交于点,如图所示,依次作正方形,正方形,…,正方形,使得点,,…在直线l上,点,,,…,在y轴正半轴上,则点的坐标为 .
16.如图所示,抛物线在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为,,,…,,将抛物线沿直线l:向上平移,得到一系列抛物线,且满足条件:①抛物线的顶点,,,…,都在直线上;②抛物线依次经过点,,,…,,则顶点的坐标为 .
三、计算题
17.已知平面直角坐标系中有一点.
(1)当点到轴的距离为时,求点的坐标;
(2)当点到两坐标轴的距离相等时,求点的坐标.
18.如图,一只甲虫在的方格(每小格边长为1)纸上沿着网格线运动,它从A处出发去看望B,C,D处的其他甲虫.规定:向上向右走为正,向下向左走为负.例如从A到B记为,从D到C记为,其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中(______,______),(______,______),;
(2)若这只甲虫从A处去P处的行走路线依次为,,,,请在图中标出P处的位置;
(3)若这只甲虫的行走路线为,请计算该甲虫走过的路程.
四、解答题
19.若点在轴上,求的值及点的坐标.
20.已知平面直角坐标系中有一点.
(1)已知点,且轴时,求点M的坐标;
(2)若点M到y轴的距离为2,求点M的坐标.
21.如图①,在平面直角坐标系中,点的坐标分别为,现同时将点分别向上平移个单位长度,再向右平移个单位长度,分别得到点的对应点,连接
问题提出:
(1)请直接写出点的坐标 , ,及四边形的面积 ﹔
拓展延伸:
(2)如图①,在坐标轴上是否存在一点,使,若存在,请求出点的坐标,若不存在,试说明理由.
迁移应用:
(3)如图②,点是线段上的个动点,连接,当点在上移动时(不与重合)给出下列结论:①的值不变,②的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
22.我们不妨约定:当满足时,则称点A为“基础点”,点为点A的“升华点”.例如.是“基础点”,则点A的“升华点”为点.
根据该约定,完成下列各题.
(1)直线上的“基础点”A坐标是________,点A的“升华点”B的坐标是________;
(2)已知两个“升华点”,,且的长为,若,求k的值;
(3)若点Q既是“基础点”,也是一个“基础点”的“升华点”,过点Q的直线l与二次函数有两个交点,点M是这两个交点的中点,求所有点M形成的图象的函数解析式,并写出对应的自变量的取值范围.
答案解析部分
1.【答案】C
【知识点】坐标与图形性质;三角形全等及其性质;坐标与图形变化﹣旋转
2.【答案】B
【知识点】用坐标表示地理位置
3.【答案】C
【知识点】点的坐标
4.【答案】D
【知识点】用坐标表示地理位置
5.【答案】C
【知识点】点的坐标与象限的关系
6.【答案】D
【知识点】点的坐标
7.【答案】B
【知识点】坐标与图形性质;含30°角的直角三角形;勾股定理;旋转的性质
8.【答案】A
【知识点】点的坐标与象限的关系
9.【答案】C
【知识点】点的坐标;平行四边形的性质
10.【答案】B
【知识点】点的坐标;坐标与图形性质
11.【答案】
【知识点】点的坐标
12.【答案】
【知识点】平移的性质;坐标与图形变化﹣平移
13.【答案】(5,-3)
【知识点】点的坐标;点的坐标与象限的关系
14.【答案】(2,65°)
【知识点】用坐标表示地理位置
15.【答案】
【知识点】点的坐标;正方形的性质;与一次函数相关的规律问题;一次函数的实际应用-几何问题
16.【答案】
【知识点】点的坐标;二次函数图象的几何变换;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
17.【答案】(1)或
(2)或
【知识点】坐标与图形性质
18.【答案】(1),
(2)解:如图,点P即为所求;
(3)解:,
答:该甲虫走过的路程是10.
【知识点】点的坐标;用坐标表示地理位置;坐标与图形变化﹣平移
19.【答案】,点的坐标为(3,0);
【知识点】坐标与图形性质;点的坐标与象限的关系
20.【答案】(1)M的坐标为
(2)点M的坐标为或
【知识点】点的坐标;坐标与图形性质
21.【答案】(1);(2)存在,M(0,6)或(0,-2)或(-3,0)或(1,0);(3)结论①正确,
【知识点】平行线的判定与性质;平移的性质;坐标与图形变化﹣平移
22.【答案】(1);
(2)
(3),自变量的取值范围为或
【知识点】一元二次方程的根与系数的关系(韦达定理);坐标与图形性质;一次函数的其他应用
21世纪教育网(www.21cnjy.com)
1 / 9
第九章 平面直角坐标系(配优)综合题
一、单选题
1.如图,将绕点O逆时针旋转90°,得到.若点的坐标为,则点A的坐标为( )
A. B. C. D.
2.如图所示,若在象棋盘上建立直角坐标系,使“将”位于点,“象”位于点,则“炮”位于点( )
A. B. C. D.
3.在平面直角坐标系中,点到轴的距离是( )
A.1 B.2 C.4 D.6
4.如图,在象棋棋盘上建立平面直角坐标系,使“马”位于点,“兵”位于点,则“帅”所在位置的坐标是( )
A. B. C. D.
5.在平面直角坐标系中,点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图,在平面直角坐标系中,是边长为个单位长度的小正方形的顶点,开始时,顶点依次放在点的位置,然后向右滚动,第次滚动使点落在点的位置,第次滚动使点落在点的位置,…,按此规律滚动下去,则第次滚动后,顶点的坐标是( )
A. B. C. D.
7.如图,在平面直角坐标系中,点在轴上,点的坐标为,将绕着点顺时针旋转,得到,则点的坐标是( )
A. B. C. D.
8.在平面直角坐标系中,点(1,2)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图,在平面直角坐标系中,点,,…,都在轴正半轴上,点在二次函数图象上,以,为邻边作平行四边形,且,延长与二次函数图象交于点;以,为邻边作平行四边形,且,延长与二次函数图象交于点;…;按此规律进行下去,若的横坐标为1,则的坐标为( )
A. B. C. D.
10.如图,动点在平面直角坐标系中按图中箭头所示方向运动,第一次从原点0运动到点,第二次运动到点,第三次运动到点,第四次运动到点,第五运动到点,第六次运动到点,…,按这样的运动规律,点的纵坐标是( )
A.-2 B.0 C.1 D.2
二、填空题
11.如图,在平面直角坐标系中,“涡状”图形的顶点坐标依次是,,,,,…,,按此规律排列下去,则的坐标是 .
12.如图,点的坐标是,点的坐标是,将沿轴向右平移得到,若,则点的坐标为 .
13.第四象限内的点尸到x轴的距离是3,到y轴的距离是5,则点P的坐标是
14.如图,线段OB,OC,OA的长度分别是1,2,3,且OC平分∠AOB.若将点A表示为(3,20°),点B表示为(1,110°),则点C可表示为 .
15.在平面直角坐标系中,直线与x轴交于点,如图所示,依次作正方形,正方形,…,正方形,使得点,,…在直线l上,点,,,…,在y轴正半轴上,则点的坐标为 .
16.如图所示,抛物线在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为,,,…,,将抛物线沿直线l:向上平移,得到一系列抛物线,且满足条件:①抛物线的顶点,,,…,都在直线上;②抛物线依次经过点,,,…,,则顶点的坐标为 .
三、计算题
17.已知平面直角坐标系中有一点.
(1)当点到轴的距离为时,求点的坐标;
(2)当点到两坐标轴的距离相等时,求点的坐标.
18.如图,一只甲虫在的方格(每小格边长为1)纸上沿着网格线运动,它从A处出发去看望B,C,D处的其他甲虫.规定:向上向右走为正,向下向左走为负.例如从A到B记为,从D到C记为,其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中(______,______),(______,______),;
(2)若这只甲虫从A处去P处的行走路线依次为,,,,请在图中标出P处的位置;
(3)若这只甲虫的行走路线为,请计算该甲虫走过的路程.
四、解答题
19.若点在轴上,求的值及点的坐标.
20.已知平面直角坐标系中有一点.
(1)已知点,且轴时,求点M的坐标;
(2)若点M到y轴的距离为2,求点M的坐标.
21.如图①,在平面直角坐标系中,点的坐标分别为,现同时将点分别向上平移个单位长度,再向右平移个单位长度,分别得到点的对应点,连接
问题提出:
(1)请直接写出点的坐标 , ,及四边形的面积 ﹔
拓展延伸:
(2)如图①,在坐标轴上是否存在一点,使,若存在,请求出点的坐标,若不存在,试说明理由.
迁移应用:
(3)如图②,点是线段上的个动点,连接,当点在上移动时(不与重合)给出下列结论:①的值不变,②的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
22.我们不妨约定:当满足时,则称点A为“基础点”,点为点A的“升华点”.例如.是“基础点”,则点A的“升华点”为点.
根据该约定,完成下列各题.
(1)直线上的“基础点”A坐标是________,点A的“升华点”B的坐标是________;
(2)已知两个“升华点”,,且的长为,若,求k的值;
(3)若点Q既是“基础点”,也是一个“基础点”的“升华点”,过点Q的直线l与二次函数有两个交点,点M是这两个交点的中点,求所有点M形成的图象的函数解析式,并写出对应的自变量的取值范围.
答案解析部分
1.【答案】C
【知识点】坐标与图形性质;三角形全等及其性质;坐标与图形变化﹣旋转
2.【答案】B
【知识点】用坐标表示地理位置
3.【答案】C
【知识点】点的坐标
4.【答案】D
【知识点】用坐标表示地理位置
5.【答案】C
【知识点】点的坐标与象限的关系
6.【答案】D
【知识点】点的坐标
7.【答案】B
【知识点】坐标与图形性质;含30°角的直角三角形;勾股定理;旋转的性质
8.【答案】A
【知识点】点的坐标与象限的关系
9.【答案】C
【知识点】点的坐标;平行四边形的性质
10.【答案】B
【知识点】点的坐标;坐标与图形性质
11.【答案】
【知识点】点的坐标
12.【答案】
【知识点】平移的性质;坐标与图形变化﹣平移
13.【答案】(5,-3)
【知识点】点的坐标;点的坐标与象限的关系
14.【答案】(2,65°)
【知识点】用坐标表示地理位置
15.【答案】
【知识点】点的坐标;正方形的性质;与一次函数相关的规律问题;一次函数的实际应用-几何问题
16.【答案】
【知识点】点的坐标;二次函数图象的几何变换;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
17.【答案】(1)或
(2)或
【知识点】坐标与图形性质
18.【答案】(1),
(2)解:如图,点P即为所求;
(3)解:,
答:该甲虫走过的路程是10.
【知识点】点的坐标;用坐标表示地理位置;坐标与图形变化﹣平移
19.【答案】,点的坐标为(3,0);
【知识点】坐标与图形性质;点的坐标与象限的关系
20.【答案】(1)M的坐标为
(2)点M的坐标为或
【知识点】点的坐标;坐标与图形性质
21.【答案】(1);(2)存在,M(0,6)或(0,-2)或(-3,0)或(1,0);(3)结论①正确,
【知识点】平行线的判定与性质;平移的性质;坐标与图形变化﹣平移
22.【答案】(1);
(2)
(3),自变量的取值范围为或
【知识点】一元二次方程的根与系数的关系(韦达定理);坐标与图形性质;一次函数的其他应用
21世纪教育网(www.21cnjy.com)
1 / 9
同课章节目录
