全等三角形的常考模型 期末复习(含答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 全等三角形的常考模型 期末复习(含答案)2024-2025学年人教版八年级数学上册 | 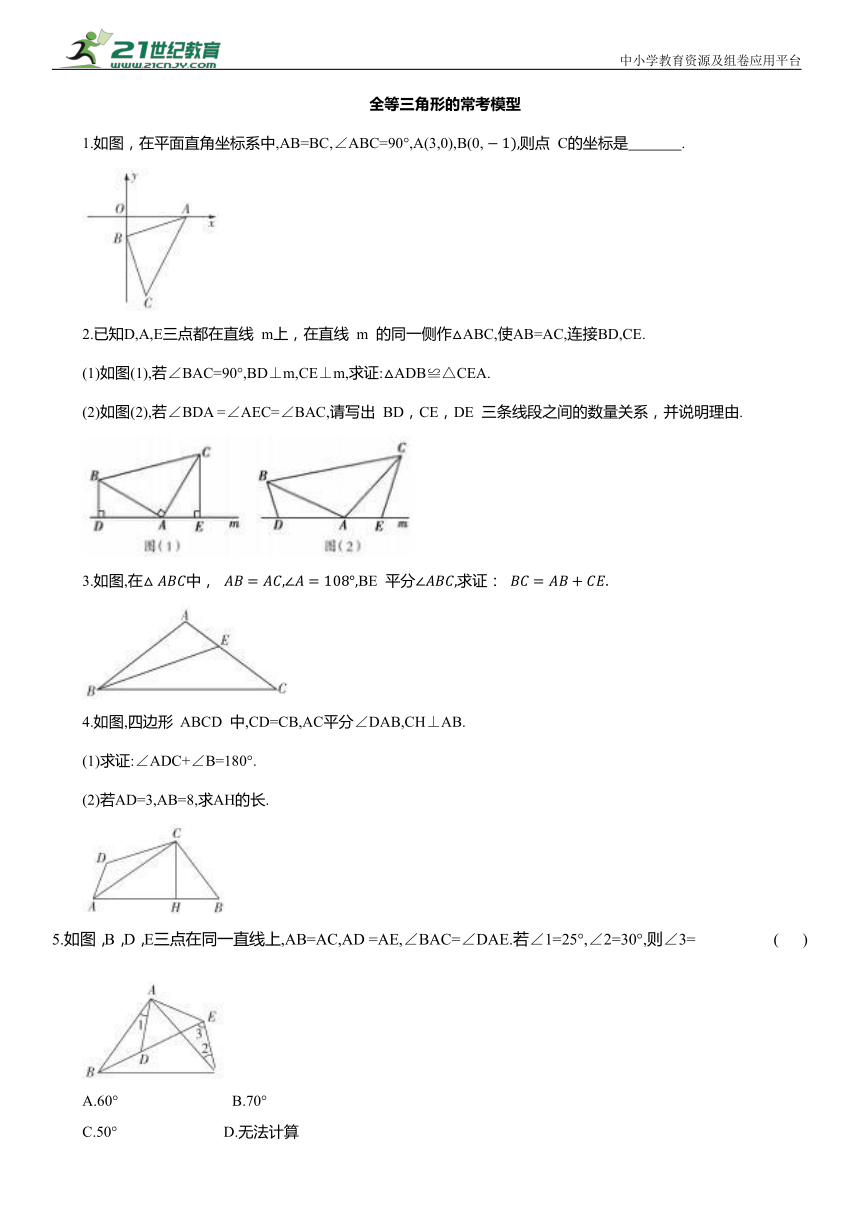 | |
| 格式 | docx | ||
| 文件大小 | 213.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 19:04:17 | ||
图片预览



文档简介
全等三角形的常考模型
1.如图,在平面直角坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0, 则点 C的坐标是 .
2.已知D,A,E三点都在直线 m上,在直线 m 的同一侧作△ABC,使AB=AC,连接BD,CE.
(1)如图(1),若∠BAC=90°,BD⊥m,CE⊥m,求证:△ADB≌△CEA.
(2)如图(2),若∠BDA =∠AEC=∠BAC,请写出 BD,CE,DE 三条线段之间的数量关系,并说明理由.
3.如图,在中, BE 平分求证:
4.如图,四边形 ABCD 中,CD=CB,AC平分∠DAB,CH⊥AB.
(1)求证:∠ADC+∠B=180°.
(2)若AD=3,AB=8,求AH的长.
5.如图,B,D,E三点在同一直线上,AB=AC,AD =AE,∠BAC=∠DAE.若∠1=25°,∠2=30°,则∠3= ( )
A.60° B.70°
C.50° D.无法计算
中小学教育资源及组卷应用平台
6.小明将两个大小不同的等腰直角三角板按如图(1)所示的方式放置在同一平面内.从图(1)中抽象出一个几何图形[如图(2)],B,C,E三点在同一条直线上,连接DC.猜想线段CD与 BE 之间的数量关系和位置关系,并证明你的结论.
7.如图,△ABD 和△ACE均为等边三角形.
(1)猜想:
①线段BE 与DC 之间的数量关系是 ;
②线段BE与DC 相交所形成的锐角的度数是 .
(2)证明(1)中②的猜想.
8.数学兴趣小组活动时,老师提出如下问题:如图(1),在△ABC中,若AB=8,AC =6,求 BC 边上的中线AD的取值范围.小明提出了如下解决方法:延长线段AD 至点E,使DE=AD,连接BE.请根据小明的方法回答下列问题.
(1)由已知和作图能得到△ADC≌△EDB 的理由是 .
A. SSS B. SAS C. AAS D. HL
(2)探究得出AD 的取值范围是 .
A.6C.1(3)如图(2),在△ABC中,CD=AB,∠BDA=∠BAD, AE 是 △ABD 的中线, 求证:∠C=∠BAE.
答案
1.(1,-4) 过点C作CD⊥y轴于点D.由题意构造全等三角形可得,AO=3,OB =1,∠ABC=90°,∠AOB =90°,∴∠OAB+∠OBA=90°,∠OBA+∠DBC=90°,∴∠OAB =∠DBC.
在△OAB 和△DBC 中,
∴BD=AO=3,DC=OB=1,∴OD=OB+BD =4,∴点C的坐标为(1,-4).
2.(1)证明:∵D,A,E三点都在直线m 上,∠BAC=90°,∴ ∠BAD+∠CAE=90°.
∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠BAD+∠ABD=90°,∴∠ABD=∠CAE.
在△ADB和△CEA中∴△ADB≌△CEA(AAS).
(2)DE=BD+CE.
理由:∵∠BDA=∠AEC=∠BAC,
∴∠BAD+∠ABD=∠BAD+∠CAE,
∴∠ABD=∠CAE.
在△ABD 和△CAE中
∴△ABD≌△CAE,∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE.
3.证明:如图,在BC上截取 BA'=BA,连接EA'.
∵∠A=108°,AB=AC,
等边对等角
∵BE平分∠ABC,
∴∠ABE=∠CBE.
在△ABE和△A'BE中,
∴△ABE≌△A'BE(SAS),
∴∠EA'C=72°,
∴CE=CA',
角平分线的性质
在Rt△CDE和Rt△CBH中
∴Rt△CDE≌Rt△CBH(HL),∴∠CDE=∠B.
∵∠CDE+∠ADC=180°,
∴∠ADC+∠B=180°.
(2)由(1)得Rt△CDE≌Rt△CBH,
∴ DE=BH.
∵AC平分∠DAB,∠E=∠AHC=90°,
∴AE=AH.
∵AD+AB=AE-DE+AH+HB=2AH,
5. B
6.猜想:BE=CD,BE⊥CD.
证明:∵ △ABC 和△ADE 均为等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,即∠BAC+∠CAE=∠DAE+∠CAE,∴∠BAE=∠CAD.
在△ABE和△ACD中
∴△ABE≌△ACD(SAS),
∴BE=CD,∠B=∠ACD.
∵∠B+∠ACB=90°,
∴∠ACD+∠ACB=90°,
∴BE⊥CD.
7.(1)①BE=CD ②60°
(2)证明:设BE交CD于点O,CD交AB 于点J.
∵△ABD 和△ACE均为等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.
在△ACD和△AEB中
∴△ACD≌△AEB(SAS),
∴∠JBO=∠JDA.
∵∠BJO=∠DJA,
∴∠BOD=∠DAB=60°,
∴线段 BE 与 DC 相交所形成的锐角的度数是60°.
8.(1)B
(2)C
解法提示:由(1)知△ADC≌△EDB,
∴BE=AC=6,AE=2AD.
∵在△ABE中,由三角形的三边关系得8-6<2AD<8+6,∴1在△ABE与△FDE中,
∴△ABE≌△FDE(SAS),
∴AB=FD,∠BAE=∠F.
∵∠ADB是△ADC的外角,
∴∠ADB=∠DAC+∠C.
∵∠ADB =∠DAB =∠BAE +∠EAD =∠F+∠EAD,
∴∠ADF=∠ADC.
∵AB=DC,∴DF=DC.
在△ADF与△ADC中,
∴△ADF≌△ADC(SAS),
∴∠C=∠F,∴∠C=∠BAE.
1.如图,在平面直角坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0, 则点 C的坐标是 .
2.已知D,A,E三点都在直线 m上,在直线 m 的同一侧作△ABC,使AB=AC,连接BD,CE.
(1)如图(1),若∠BAC=90°,BD⊥m,CE⊥m,求证:△ADB≌△CEA.
(2)如图(2),若∠BDA =∠AEC=∠BAC,请写出 BD,CE,DE 三条线段之间的数量关系,并说明理由.
3.如图,在中, BE 平分求证:
4.如图,四边形 ABCD 中,CD=CB,AC平分∠DAB,CH⊥AB.
(1)求证:∠ADC+∠B=180°.
(2)若AD=3,AB=8,求AH的长.
5.如图,B,D,E三点在同一直线上,AB=AC,AD =AE,∠BAC=∠DAE.若∠1=25°,∠2=30°,则∠3= ( )
A.60° B.70°
C.50° D.无法计算
中小学教育资源及组卷应用平台
6.小明将两个大小不同的等腰直角三角板按如图(1)所示的方式放置在同一平面内.从图(1)中抽象出一个几何图形[如图(2)],B,C,E三点在同一条直线上,连接DC.猜想线段CD与 BE 之间的数量关系和位置关系,并证明你的结论.
7.如图,△ABD 和△ACE均为等边三角形.
(1)猜想:
①线段BE 与DC 之间的数量关系是 ;
②线段BE与DC 相交所形成的锐角的度数是 .
(2)证明(1)中②的猜想.
8.数学兴趣小组活动时,老师提出如下问题:如图(1),在△ABC中,若AB=8,AC =6,求 BC 边上的中线AD的取值范围.小明提出了如下解决方法:延长线段AD 至点E,使DE=AD,连接BE.请根据小明的方法回答下列问题.
(1)由已知和作图能得到△ADC≌△EDB 的理由是 .
A. SSS B. SAS C. AAS D. HL
(2)探究得出AD 的取值范围是 .
A.6
答案
1.(1,-4) 过点C作CD⊥y轴于点D.由题意构造全等三角形可得,AO=3,OB =1,∠ABC=90°,∠AOB =90°,∴∠OAB+∠OBA=90°,∠OBA+∠DBC=90°,∴∠OAB =∠DBC.
在△OAB 和△DBC 中,
∴BD=AO=3,DC=OB=1,∴OD=OB+BD =4,∴点C的坐标为(1,-4).
2.(1)证明:∵D,A,E三点都在直线m 上,∠BAC=90°,∴ ∠BAD+∠CAE=90°.
∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠BAD+∠ABD=90°,∴∠ABD=∠CAE.
在△ADB和△CEA中∴△ADB≌△CEA(AAS).
(2)DE=BD+CE.
理由:∵∠BDA=∠AEC=∠BAC,
∴∠BAD+∠ABD=∠BAD+∠CAE,
∴∠ABD=∠CAE.
在△ABD 和△CAE中
∴△ABD≌△CAE,∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE.
3.证明:如图,在BC上截取 BA'=BA,连接EA'.
∵∠A=108°,AB=AC,
等边对等角
∵BE平分∠ABC,
∴∠ABE=∠CBE.
在△ABE和△A'BE中,
∴△ABE≌△A'BE(SAS),
∴∠EA'C=72°,
∴CE=CA',
角平分线的性质
在Rt△CDE和Rt△CBH中
∴Rt△CDE≌Rt△CBH(HL),∴∠CDE=∠B.
∵∠CDE+∠ADC=180°,
∴∠ADC+∠B=180°.
(2)由(1)得Rt△CDE≌Rt△CBH,
∴ DE=BH.
∵AC平分∠DAB,∠E=∠AHC=90°,
∴AE=AH.
∵AD+AB=AE-DE+AH+HB=2AH,
5. B
6.猜想:BE=CD,BE⊥CD.
证明:∵ △ABC 和△ADE 均为等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,即∠BAC+∠CAE=∠DAE+∠CAE,∴∠BAE=∠CAD.
在△ABE和△ACD中
∴△ABE≌△ACD(SAS),
∴BE=CD,∠B=∠ACD.
∵∠B+∠ACB=90°,
∴∠ACD+∠ACB=90°,
∴BE⊥CD.
7.(1)①BE=CD ②60°
(2)证明:设BE交CD于点O,CD交AB 于点J.
∵△ABD 和△ACE均为等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.
在△ACD和△AEB中
∴△ACD≌△AEB(SAS),
∴∠JBO=∠JDA.
∵∠BJO=∠DJA,
∴∠BOD=∠DAB=60°,
∴线段 BE 与 DC 相交所形成的锐角的度数是60°.
8.(1)B
(2)C
解法提示:由(1)知△ADC≌△EDB,
∴BE=AC=6,AE=2AD.
∵在△ABE中,由三角形的三边关系得8-6<2AD<8+6,∴1
∴△ABE≌△FDE(SAS),
∴AB=FD,∠BAE=∠F.
∵∠ADB是△ADC的外角,
∴∠ADB=∠DAC+∠C.
∵∠ADB =∠DAB =∠BAE +∠EAD =∠F+∠EAD,
∴∠ADF=∠ADC.
∵AB=DC,∴DF=DC.
在△ADF与△ADC中,
∴△ADF≌△ADC(SAS),
∴∠C=∠F,∴∠C=∠BAE.
同课章节目录
