特殊平行四边形的动点问题 期末复习练习(含答案)2024-2025北师大版九年级数学上册
文档属性
| 名称 | 特殊平行四边形的动点问题 期末复习练习(含答案)2024-2025北师大版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 315.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 19:08:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
特殊平行四边形的动点问题
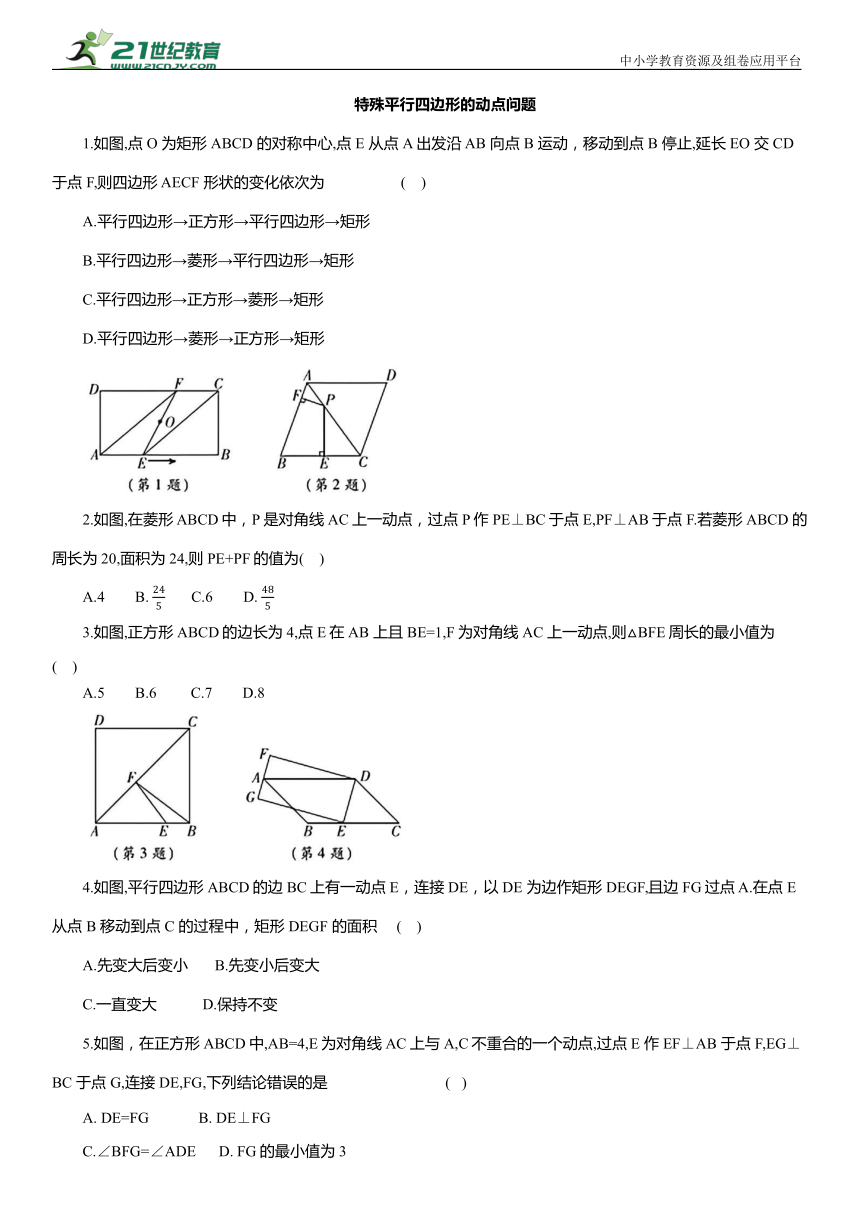
1.如图,点O 为矩形ABCD 的对称中心,点 E 从点A 出发沿 AB 向点 B 运动,移动到点 B 停止,延长 EO 交 CD 于点 F,则四边形 AECF 形状的变化依次为 ( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
2.如图,在菱形 ABCD中,P是对角线AC上一动点,过点 P 作 PE⊥BC于点E,PF⊥AB于点 F.若菱形ABCD 的周长为20,面积为24,则 PE+PF的值为( )
A.4 B. C.6 D.
3.如图,正方形ABCD的边长为4,点 E在AB 上且BE=1,F为对角线AC 上一动点,则△BFE周长的最小值为 ( )
A.5 B.6 C.7 D.8
4.如图,平行四边形ABCD的边 BC上有一动点E,连接DE,以DE 为边作矩形 DEGF,且边 FG过点 A.在点 E 从点 B 移动到点 C 的过程中,矩形 DEGF 的面积 ( )
A.先变大后变小 B.先变小后变大
C.一直变大 D.保持不变
5.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点 E 作 EF⊥AB 于点 F,EG⊥BC 于点 G,连接 DE,FG,下列结论错误的是 ( )
A. DE=FG B. DE⊥FG
C.∠BFG=∠ADE D. FG的最小值为3
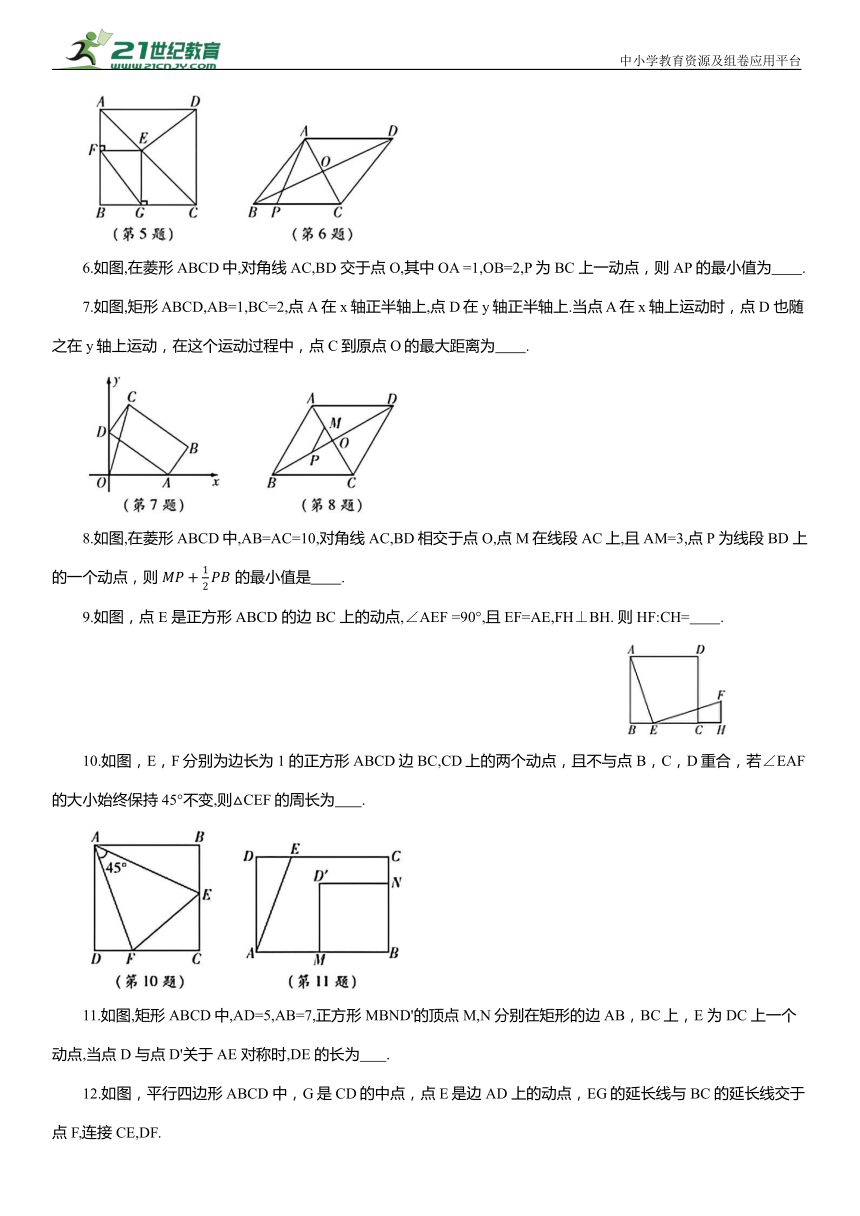
6.如图,在菱形ABCD中,对角线AC,BD 交于点O,其中OA =1,OB=2,P为 BC 上一动点,则AP 的最小值为 .
7.如图,矩形 ABCD,AB=1,BC=2,点A在x轴正半轴上,点D在y轴正半轴上.当点 A 在x轴上运动时,点D 也随之在y轴上运动,在这个运动过程中,点C到原点O的最大距离为 .
8.如图,在菱形ABCD中,AB=AC=10,对角线AC,BD相交于点O,点M在线段AC上,且AM=3,点 P 为线段 BD 上的一个动点,则 的最小值是 .
9.如图,点E 是正方形ABCD 的边 BC 上的动点,∠AEF =90°,且EF=AE,FH⊥BH. 则HF:CH= .
10.如图,E,F分别为边长为1 的正方形ABCD边BC,CD上的两个动点,且不与点 B,C,D重合,若∠EAF 的大小始终保持45°不变,则△CEF的周长为 .
11.如图,矩形ABCD中,AD=5,AB=7,正方形 MBND'的顶点 M,N分别在矩形的边AB,BC上,E 为 DC 上一个动点,当点 D 与点 D'关于AE 对称时,DE 的长为 .
12.如图,平行四边形ABCD 中,G是CD的中点,点E是边AD 上的动点,EG的延长线与 BC 的延长线交于点 F,连接CE,DF.
(1)求证:四边形CEDF 是平行四边形.
(2)若AB=5cm,BC=10 cm,∠B=60°.
①当AE= cm时,四边形 CEDF是矩形.
②当AE= cm时,四边形 CEDF是菱形.
13.如图,在矩形ABCD 中,AD=8,CD=20,P是AB上一动点,M,N,E分别是 PD,PC,CD 的中点.
(1)求证:四边形 PMEN 是平行四边形.
(2)若四边形 PMEN 是菱形,请求出 AP的长.
(3)四边形 PMEN 有可能是矩形吗 若有可能,求出 AP 的长;若不可能,请说明理由.
1. B 连接AC,由对角线互相平分的四边形为平行四边形可知,点E 在运动过程中,四边形AECF 始终为平行四边形.特殊地,当EF⊥AC时,四边形AECF 为菱形,当点 E 与点 B 重合时,四边形AECF 是矩形.故四边形AECF 的形状依次为平行四边形→菱形→平行四边形→矩形.
2. B 连接BP,∵四边形ABCD 为菱形,且周长为20,
3. B ∵ 四边形 ABCD 是正方形,∴点 B 与点 D 关于直线AC 对称.如图,连接 DE 交 AC于点 F,则 BF = DF,此时△BFE 的周长有最小值,最小值为DF+EF+BE=DE+BE.∵AB=4,BE=1,∴AE=3.在 Rt△ADE中,根据勾股定理,得 6,∴△BFE周长的最小值为6.
4. D (转化思想)连接AE,∵矩形 DEGF 的面积.矩形 DEGF 的面积保持不变.
5. D 如图,连接BE,交 FG 于点 O.∵ EF⊥AB,EG⊥BC,∴∠EFB= ∠EGB = 90°.∵∠ABC= 90°, ∴ 四 边 形EFBG 为矩形,∴ FG = BE,OB=OF=OE =OG.∵ 四边形 ABCD 为正方形,∴AB=AD,∠BAC=∠DAC=45°.在△ABE
和△ADE 中, △ADE,∴ BE = DE.∴DE = FG,∴ A 选项正确.延长 DE 交 FG 于点 M,交 FB 于点 H,∵△ABE≌△ADE,∴ ∠ABE =∠ADE.由上知OB = OF,∴ ∠OFB = ∠ABE,∴ ∠OFB =∠ADE.∵ ∠BAD =90°,∴ ∠ADE +∠AHD =90°,∴∠OFB+∠AHD=90°,即∠FMH=90°,∴ DE⊥FG,∴ B 选项正确.由上知∠OFB =∠ADE,即∠BFG=∠ADE.∴C 选项正确.∵E为AC上一动点,且由上知DE=FG,∴当DE⊥AC时,DE 最小.∵AD=CD=4,∠ADC=90°, ∴ FG的最小值为2 ,∴ D选项错误.
四边形 ABCD 是菱形,∴ AB = BC,AC⊥BD,AO=CO=1,BO=DO=2,∴AC=2, P为 BC上一动点,∴当AP⊥BC 时,AP 有最小值 ∴AP的最小值为
如图,取AD 的中点H,连接 CH,OH,∵点 H是AD的中点,∴AH =DH= 0 点H 是 AD 的中点. 在△OCH 中,CO如图,过点 P 作 PE⊥BC 于点 E,∵四边
形ABCD 是菱形,AB =AC=10,∴ AB = BC = AC = 10,∠ABD = ∠CBD,∴ △ABC是等边三角形,∴ ∠ABC =∠ACB=60°,∴∠CBD=30°.∵ PE⊥BC,∴PE = ∴当点M,P,E共线,即 ME⊥BC 时,PM +PE 有最小值为ME.此时
9.1:1 ∵四边形ABCD 是正方形,∴∠B=90°,AB= BC. ∵ FH ⊥ BH,∴ ∠H = 90°= ∠B,∠F= 90° - ∠FEH, ∵ ∠AEF = 90°,∴ ∠AEB=90° - ∠FEH,∴ ∠AEB = ∠F.在△ABE和△EHF中,
∴EH=AB=BC,HF=BE,∴EH-EC=BC-EC,即CH=BE,∴HF:CH=1:1.
10.2 如图,将△ABE 绕点A 顺时针旋转90°,得到△ADG.∵四边形ABCD 是正方形,∴ AB = BC = CD =AD = 1,∠BAD =90°. 由 旋 转 得△ABE≌△ADG,∴AE=AG,BE =DG,∠BAE =∠DAG.∵ ∠EAF=45°,∴∠DAF+∠BAE =∠DAF+∠DAG =45°,∴ ∠EAF =∠FAG =45°.∵ AF =AF,∴△EAF≌△GAF,∴ EF =GF,∴EF=GD+DF =BE+DF,∴△ECF 的周长=EF+EC +CF=BE+DF+EC+CF=BC+CD=2.
11. 或
(分类讨论思想)如图,连接ED',AD',延长 MD'交 DC 于点 P.设MD'=ND'=BM=x.则AM =AB-BM =7-x. 当点 D 与点 D'关于 AE 对称时,可得AD'=AD =5.∴在Rt△AD'M中, 即 解得x=3或4,即 MD'=3或4.设ED=ED'=a.①当MD'=3时,AM =7-3 =4,D'P=5-3 =2,EP =4-a,∴ 在Rt△EPD'中, 即 解得 即 ②当MD'=4时,AM=7-4=3,D'P=5-4=1,EP=3-a,∴在 Rt△EPD'中. 即 解得 即 综上所述,DE 的长为 或
12.【参考答案】(1)证明:∵四边形ABCD 是平行四边形,
∴AD∥BF,∴∠DEG=∠CFG.
∵G是CD的中点,∴GD=GC.
在△GED 和△GFC中,
∴△GED≌△GFC(AAS),∴DE=CF.
∵DE∥CF,∴四边形CEDF是平行四边形.
(2)①7.5
(2)解法提示:过点A作AP⊥BC于点 P.如图,
∵AB=5cm,∠B=60°,
∴∠BAP=30°.
∴PC=10-2.5=7.5(cm).
∵四边形CEDF 是矩形.
∴易得四边形AECP 是矩形,
∴AE=PC=7.5cm.
②5
解法提示:∵ 四边形 CEDF 是菱形,
∴CE=ED.
∵四边形ABCD是平行四边形,且∠B=60°,
∴ ∠CDE=∠B=60°,
∴ △CDE是等边三角形,
∴ED=CD=5cm,∴AE=5cm.
13.【参考答案】(1)证明:∵M,N,E分别是 PD,PC,CD的中点,
∴ME∥PC,EN∥PD,
∴ 四边形 PMEN 是平行四边形.
(2)∵四边形ABCD 是矩形,
∴AB=CD=20,AD=BC,∠A=∠B=90°.
∵四边形PMEN是菱形,
∴PM=PN.
∵M,N分别是PD,PC的中点,
∴PD=PC,
∴Rt△APD≌Rt△BPC,
(3)四边形 PMEN有可能是矩形.
由(1)知,四边形 PMEN 是平行四边形,要使平行四边形 PMEN 是矩形,则∠DPC=90°.
设PA=x,PB=20-x,
在 Rt△DPC中,由勾股定理得 即
解得x=4或x=16.
∴当AP =4 或AP =16时,四边形 PMEN 是矩形.
特殊平行四边形的动点问题
1.如图,点O 为矩形ABCD 的对称中心,点 E 从点A 出发沿 AB 向点 B 运动,移动到点 B 停止,延长 EO 交 CD 于点 F,则四边形 AECF 形状的变化依次为 ( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
2.如图,在菱形 ABCD中,P是对角线AC上一动点,过点 P 作 PE⊥BC于点E,PF⊥AB于点 F.若菱形ABCD 的周长为20,面积为24,则 PE+PF的值为( )
A.4 B. C.6 D.
3.如图,正方形ABCD的边长为4,点 E在AB 上且BE=1,F为对角线AC 上一动点,则△BFE周长的最小值为 ( )
A.5 B.6 C.7 D.8
4.如图,平行四边形ABCD的边 BC上有一动点E,连接DE,以DE 为边作矩形 DEGF,且边 FG过点 A.在点 E 从点 B 移动到点 C 的过程中,矩形 DEGF 的面积 ( )
A.先变大后变小 B.先变小后变大
C.一直变大 D.保持不变
5.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点 E 作 EF⊥AB 于点 F,EG⊥BC 于点 G,连接 DE,FG,下列结论错误的是 ( )
A. DE=FG B. DE⊥FG
C.∠BFG=∠ADE D. FG的最小值为3
6.如图,在菱形ABCD中,对角线AC,BD 交于点O,其中OA =1,OB=2,P为 BC 上一动点,则AP 的最小值为 .
7.如图,矩形 ABCD,AB=1,BC=2,点A在x轴正半轴上,点D在y轴正半轴上.当点 A 在x轴上运动时,点D 也随之在y轴上运动,在这个运动过程中,点C到原点O的最大距离为 .
8.如图,在菱形ABCD中,AB=AC=10,对角线AC,BD相交于点O,点M在线段AC上,且AM=3,点 P 为线段 BD 上的一个动点,则 的最小值是 .
9.如图,点E 是正方形ABCD 的边 BC 上的动点,∠AEF =90°,且EF=AE,FH⊥BH. 则HF:CH= .
10.如图,E,F分别为边长为1 的正方形ABCD边BC,CD上的两个动点,且不与点 B,C,D重合,若∠EAF 的大小始终保持45°不变,则△CEF的周长为 .
11.如图,矩形ABCD中,AD=5,AB=7,正方形 MBND'的顶点 M,N分别在矩形的边AB,BC上,E 为 DC 上一个动点,当点 D 与点 D'关于AE 对称时,DE 的长为 .
12.如图,平行四边形ABCD 中,G是CD的中点,点E是边AD 上的动点,EG的延长线与 BC 的延长线交于点 F,连接CE,DF.
(1)求证:四边形CEDF 是平行四边形.
(2)若AB=5cm,BC=10 cm,∠B=60°.
①当AE= cm时,四边形 CEDF是矩形.
②当AE= cm时,四边形 CEDF是菱形.
13.如图,在矩形ABCD 中,AD=8,CD=20,P是AB上一动点,M,N,E分别是 PD,PC,CD 的中点.
(1)求证:四边形 PMEN 是平行四边形.
(2)若四边形 PMEN 是菱形,请求出 AP的长.
(3)四边形 PMEN 有可能是矩形吗 若有可能,求出 AP 的长;若不可能,请说明理由.
1. B 连接AC,由对角线互相平分的四边形为平行四边形可知,点E 在运动过程中,四边形AECF 始终为平行四边形.特殊地,当EF⊥AC时,四边形AECF 为菱形,当点 E 与点 B 重合时,四边形AECF 是矩形.故四边形AECF 的形状依次为平行四边形→菱形→平行四边形→矩形.
2. B 连接BP,∵四边形ABCD 为菱形,且周长为20,
3. B ∵ 四边形 ABCD 是正方形,∴点 B 与点 D 关于直线AC 对称.如图,连接 DE 交 AC于点 F,则 BF = DF,此时△BFE 的周长有最小值,最小值为DF+EF+BE=DE+BE.∵AB=4,BE=1,∴AE=3.在 Rt△ADE中,根据勾股定理,得 6,∴△BFE周长的最小值为6.
4. D (转化思想)连接AE,∵矩形 DEGF 的面积.矩形 DEGF 的面积保持不变.
5. D 如图,连接BE,交 FG 于点 O.∵ EF⊥AB,EG⊥BC,∴∠EFB= ∠EGB = 90°.∵∠ABC= 90°, ∴ 四 边 形EFBG 为矩形,∴ FG = BE,OB=OF=OE =OG.∵ 四边形 ABCD 为正方形,∴AB=AD,∠BAC=∠DAC=45°.在△ABE
和△ADE 中, △ADE,∴ BE = DE.∴DE = FG,∴ A 选项正确.延长 DE 交 FG 于点 M,交 FB 于点 H,∵△ABE≌△ADE,∴ ∠ABE =∠ADE.由上知OB = OF,∴ ∠OFB = ∠ABE,∴ ∠OFB =∠ADE.∵ ∠BAD =90°,∴ ∠ADE +∠AHD =90°,∴∠OFB+∠AHD=90°,即∠FMH=90°,∴ DE⊥FG,∴ B 选项正确.由上知∠OFB =∠ADE,即∠BFG=∠ADE.∴C 选项正确.∵E为AC上一动点,且由上知DE=FG,∴当DE⊥AC时,DE 最小.∵AD=CD=4,∠ADC=90°, ∴ FG的最小值为2 ,∴ D选项错误.
四边形 ABCD 是菱形,∴ AB = BC,AC⊥BD,AO=CO=1,BO=DO=2,∴AC=2, P为 BC上一动点,∴当AP⊥BC 时,AP 有最小值 ∴AP的最小值为
如图,取AD 的中点H,连接 CH,OH,∵点 H是AD的中点,∴AH =DH= 0 点H 是 AD 的中点. 在△OCH 中,CO
形ABCD 是菱形,AB =AC=10,∴ AB = BC = AC = 10,∠ABD = ∠CBD,∴ △ABC是等边三角形,∴ ∠ABC =∠ACB=60°,∴∠CBD=30°.∵ PE⊥BC,∴PE = ∴当点M,P,E共线,即 ME⊥BC 时,PM +PE 有最小值为ME.此时
9.1:1 ∵四边形ABCD 是正方形,∴∠B=90°,AB= BC. ∵ FH ⊥ BH,∴ ∠H = 90°= ∠B,∠F= 90° - ∠FEH, ∵ ∠AEF = 90°,∴ ∠AEB=90° - ∠FEH,∴ ∠AEB = ∠F.在△ABE和△EHF中,
∴EH=AB=BC,HF=BE,∴EH-EC=BC-EC,即CH=BE,∴HF:CH=1:1.
10.2 如图,将△ABE 绕点A 顺时针旋转90°,得到△ADG.∵四边形ABCD 是正方形,∴ AB = BC = CD =AD = 1,∠BAD =90°. 由 旋 转 得△ABE≌△ADG,∴AE=AG,BE =DG,∠BAE =∠DAG.∵ ∠EAF=45°,∴∠DAF+∠BAE =∠DAF+∠DAG =45°,∴ ∠EAF =∠FAG =45°.∵ AF =AF,∴△EAF≌△GAF,∴ EF =GF,∴EF=GD+DF =BE+DF,∴△ECF 的周长=EF+EC +CF=BE+DF+EC+CF=BC+CD=2.
11. 或
(分类讨论思想)如图,连接ED',AD',延长 MD'交 DC 于点 P.设MD'=ND'=BM=x.则AM =AB-BM =7-x. 当点 D 与点 D'关于 AE 对称时,可得AD'=AD =5.∴在Rt△AD'M中, 即 解得x=3或4,即 MD'=3或4.设ED=ED'=a.①当MD'=3时,AM =7-3 =4,D'P=5-3 =2,EP =4-a,∴ 在Rt△EPD'中, 即 解得 即 ②当MD'=4时,AM=7-4=3,D'P=5-4=1,EP=3-a,∴在 Rt△EPD'中. 即 解得 即 综上所述,DE 的长为 或
12.【参考答案】(1)证明:∵四边形ABCD 是平行四边形,
∴AD∥BF,∴∠DEG=∠CFG.
∵G是CD的中点,∴GD=GC.
在△GED 和△GFC中,
∴△GED≌△GFC(AAS),∴DE=CF.
∵DE∥CF,∴四边形CEDF是平行四边形.
(2)①7.5
(2)解法提示:过点A作AP⊥BC于点 P.如图,
∵AB=5cm,∠B=60°,
∴∠BAP=30°.
∴PC=10-2.5=7.5(cm).
∵四边形CEDF 是矩形.
∴易得四边形AECP 是矩形,
∴AE=PC=7.5cm.
②5
解法提示:∵ 四边形 CEDF 是菱形,
∴CE=ED.
∵四边形ABCD是平行四边形,且∠B=60°,
∴ ∠CDE=∠B=60°,
∴ △CDE是等边三角形,
∴ED=CD=5cm,∴AE=5cm.
13.【参考答案】(1)证明:∵M,N,E分别是 PD,PC,CD的中点,
∴ME∥PC,EN∥PD,
∴ 四边形 PMEN 是平行四边形.
(2)∵四边形ABCD 是矩形,
∴AB=CD=20,AD=BC,∠A=∠B=90°.
∵四边形PMEN是菱形,
∴PM=PN.
∵M,N分别是PD,PC的中点,
∴PD=PC,
∴Rt△APD≌Rt△BPC,
(3)四边形 PMEN有可能是矩形.
由(1)知,四边形 PMEN 是平行四边形,要使平行四边形 PMEN 是矩形,则∠DPC=90°.
设PA=x,PB=20-x,
在 Rt△DPC中,由勾股定理得 即
解得x=4或x=16.
∴当AP =4 或AP =16时,四边形 PMEN 是矩形.
同课章节目录
