特殊平行四边形的折叠问题 期末复习练习(含答案)2024-2025北师大版九年级数学上册
文档属性
| 名称 | 特殊平行四边形的折叠问题 期末复习练习(含答案)2024-2025北师大版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 302.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 19:10:23 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
特殊平行四边形的折叠问题
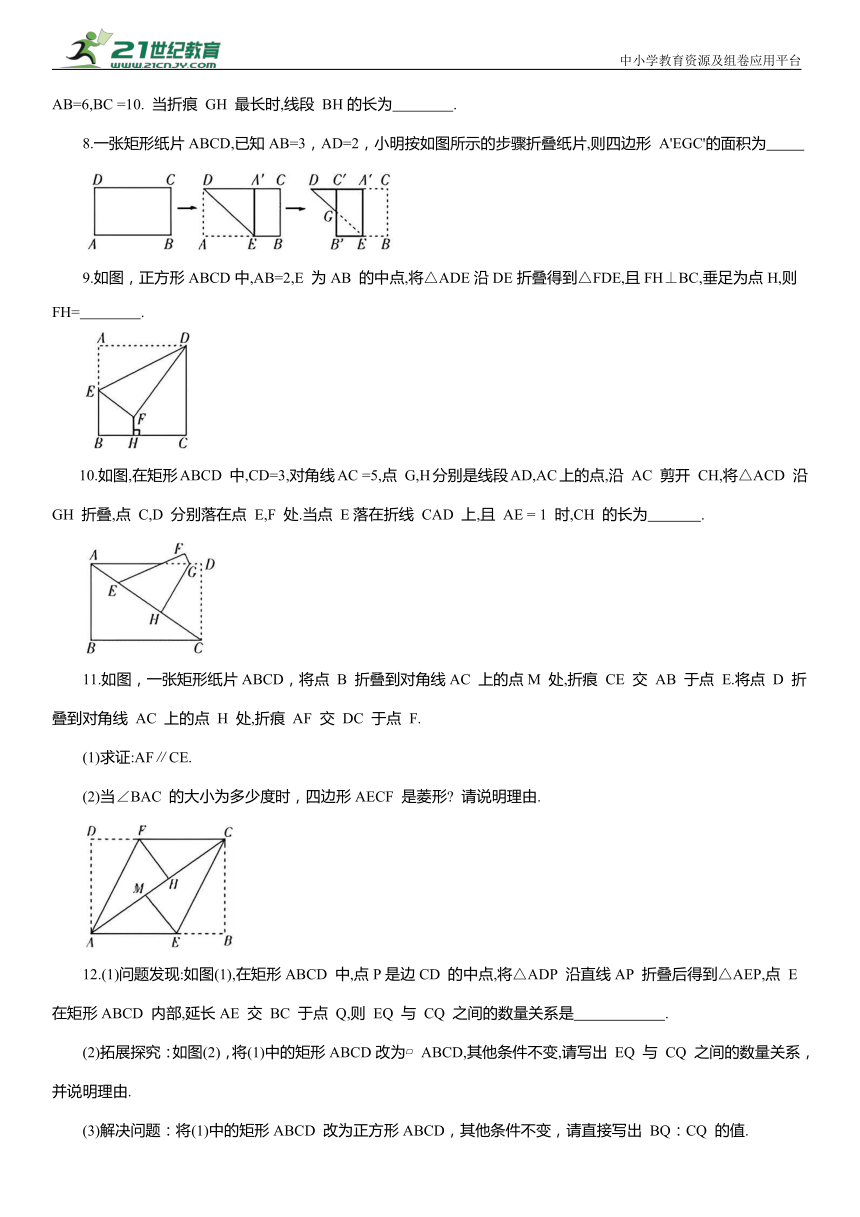
1.如图,已知矩形ABCD,将△BCD沿对角线 BD 折叠,记点 C 的对应点为点 C',若 ,则∠BDC 的度数为 ( )
A.55° B.50° C.60° D.65°
2.如图,在菱形纸ABCD中,∠A=60°,点 E 在 BC 边上,将菱形纸片ABCD 沿 DE 折叠,点 C 的对应点为点 C',且 DC'垂直平分AB,则∠DEC的度数为 ( )
A.30° B.45° C.60° D.75°
3.如图,在菱形 ABCD中,∠A =120°,E 是 AD 上的点,沿 BE 折叠△ABE,点 A 恰好落在 BD 上的点 F 处,连接CF,那么∠BFC 的度数是 .
4.如图,在平面直角坐标系中,矩形 ABCO 的边 CO,OA 分别在 x 轴、y轴上,点E 在边 BC 上,将该矩形沿 AE 折叠,点 B 恰好落在边 OC 上的 F 处.若OA = 6,AB = 10, 则点 E 的坐标是 .
5.如图,在正方形ABCD 中,E 是 BC 边上的一点,将正方形边 AB 沿 AE 折叠到 AF,延长 EF交DC 于点G,连接AG,则∠EAG= .
6.如图,在边长为2 的菱形 ABCD 中,∠D =45°,点 E 在 BC 边上,将△ABE沿 AE 所在的直线折叠得到△AB E,AB 交CD 于点 F,且EB 过点 C,则 CB 的长度为 .
7.如图,折叠矩形纸片 ABCD,使点 B 的对应点 E 落在CD边上,GH 为折痕,已知AB=6,BC =10. 当折痕 GH 最长时,线段 BH的长为 .
8.一张矩形纸片ABCD,已知AB=3,AD=2,小明按如图所示的步骤折叠纸片,则四边形 A'EGC'的面积为
9.如图,正方形ABCD中,AB=2,E 为AB 的中点,将△ADE沿DE折叠得到△FDE,且FH⊥BC,垂足为点H,则FH= .
10.如图,在矩形ABCD 中,CD=3,对角线AC =5,点 G,H分别是线段AD,AC上的点,沿 AC 剪开 CH,将△ACD 沿GH 折叠,点 C,D 分别落在点 E,F 处.当点 E落在折线 CAD 上,且 AE = 1 时,CH 的长为 .
11.如图,一张矩形纸片ABCD,将点 B 折叠到对角线AC 上的点M 处,折痕 CE 交 AB 于点 E.将点 D 折叠到对角线 AC 上的点 H 处,折痕 AF 交 DC 于点 F.
(1)求证:AF∥CE.
(2)当∠BAC 的大小为多少度时,四边形AECF 是菱形 请说明理由.
12.(1)问题发现:如图(1),在矩形ABCD 中,点P是边CD 的中点,将△ADP 沿直线AP 折叠后得到△AEP,点 E 在矩形ABCD 内部,延长AE 交 BC 于点 Q,则 EQ 与 CQ 之间的数量关系是 .
(2)拓展探究:如图(2),将(1)中的矩形ABCD改为 ABCD,其他条件不变,请写出 EQ 与 CQ 之间的数量关系,并说明理由.
(3)解决问题:将(1)中的矩形ABCD 改为正方形ABCD,其他条件不变,请直接写出 BQ:CQ 的值.
参考答案
A 由折叠可得∠BDC=∠BDC',∴ ∠ADB =∠BDC'-∠ADC'=∠BDC-20°.
∵ ∠ADB +∠BDC=90°,∴∠BDC-20°+∠BDC=90°,解得∠BDC=55°.
∵四边形ABCD 是矩形.∴ ∠ADC=90°.由折叠可得∠BDC=
2. D 如图,连接BD,AB与DC'的交点记为 P.∵ 四边 形 ABCD 为菱 形,∴AB=AD.∵ ∠A =60°,∴△ABD 为等边三角形,∠ADC = 120°,∠C=60°.∵DC'垂直平分AB,∴∠ADP=∠BDP=30°,∴∠PDC=90°.由折叠可得∠CDE=∠PDE=45°,∴∠DEC=180°-(∠CDE+∠C)=75°.
3.75° ∵四边形ABCD 是菱形,∴AB=BC,∠A +∠ABC=180°,BD 平分∠ABC.∵ ∠A=120°,∴∠ABC=60°,∴∠FBC=30°.根据折叠可得AB=BF,∴FB=BC,∴∠BFC=∠BCF= (180°-30°)=75°.
设CE=a,则BE=6-a,由折叠可知,EF = BE = 6 - a,AF = AB = 10,∴ 在Rt△AOF中, 8,∴CF=OC--OF = 10 - 8 =2.∵ ∠ECF =90°,∴在Rt△CEF中, 解得 点E的坐标是
5.45°∵ 四边形 ABCD 是正方形,∴ AB =AD,
由折叠可知AB =AF,∠ABE = ∠AFE = ∠AFG = 90°,∠BAE = AD=AF,∴ Rt△AGD≌Rt△AGF,∴∠GAF =∠GAD, ∴ ∠EAG = ∠EAF + ∠GAF =
·四边形ABCD 是菱形,∴AB=BC=2,∠B=∠D =45°.∵将△ABE 沿AE 所在的直线折叠得到△AB E,∴BE=B E,AB =AB ,∴∠B =∠B=45°,∴∠BAB =90°,∴BB =
7.6.8 由题意知,当点 E 与点 D 重合时,GH 最长,设BH=x,则 CH =10-x,HE =BH=x.在Rt△HCE 中,由勾股定理得, 即 解得x=6.8.
由折叠可得, 2,A'C'=A'C=3-2=1,∠A'DE=45°,∴C'G=C'D=1,∴ 四边形A'EGC'的面积
如图,过点 F 作MN∥BC,交AB 于点M,交 CD 于点 N. ∵ 四边形ABCD 是正方形,∴ ∠B =∠C= 90°. ∵ MN ∥ BC,∴∠AMF=∠B =90°,∠DNF =∠C = 90°, ∴∠EMF=∠DNF=90°.∵正方形ABCD 中,AB =2,E 为AB的中点,∴ 由折叠得 DF =AD =AB =2,EF= BE = AE = l, ∠A = ∠EFD = 90°,∴∠EFM +∠DFN = ∠DFN + ∠NDF =90°, 设 FH =BM =x,则EM =1-x,FN=2EM =2(1-x) =2-2x,∴ FM =2-FN=2-(2-2x) =2x.在 Rt△EMF 中,由勾股定理得 (2x) ,解得x =0(舍去)
10.2 或
∵在矩形ABCD 中,AC=5. CD=3.∴AD= 当点 E 落在 AC 上时,如图(1),∵ 将△ACD 沿 GH 折叠,∴ CH = EH.∵ AE =1.∴EC=4,∴CH=2.当点 E 落在 AD 上时,如图(2),连接EC.过点E 作 EN⊥AC 于点 将△ACD 沿GH折叠, 综上所述,CH的长为2或
11.(1)证明:∵ 四边形 ABCD 为矩形,
∴AD∥BC,∴∠DAC=∠BCA.
由折叠知
∴∠HAF=∠MCE,∴AF∥CE.
(2)当∠BAC=30°时,四边形AECF 是菱形.理由如下:
∵四边形ABCD 是矩形,
∴∠B=∠BAD=90°,AB∥CD,
由(1)知AF∥CE,
∴ 四边形AECF 是平行四边形.
要使四边形AECF 是菱形,
则AE=EC,即∠EAC=∠ECA.
由折叠可得∠ECA=∠ECB,
∴∠BAC=∠ECA =∠ECB,
∴∠BAC=30°.
12.(1)EQ=CQ
解法提示:连接PQ,
∵点 P为CD的中点,∴ DP=CP.
由折叠的性质可得 DP = PE,∠PEA =∠PDA=90°,
∴PC=PE,∠PCQ=∠PEQ=90°.
∵PQ =PQ,
∴Rt△PEQ≌Rt△PCQ,∴EQ=CQ.
(2)EQ=CQ.
理由:连接EC,
由折叠的性质可知,DP=EP,∠D=∠PEA.
∵点 P是CD的中点,
∴DP=CP,∴EP=CP,
∴ ∠PEC=∠PCE.
∵四边形ABCD 是平行四边形,
∴AD∥BC,∴∠D+∠PCQ=180°.
∵∠PEA+∠PEQ=180°,
∴∠PCQ=∠PEQ.
∴∠PCQ--∠PCE=∠PEQ-∠PEC,
即∠QCE=∠QEC,∴EQ=CQ.
(3)BQ:CQ 的值为3.
解法提示:
设AD=1,CQ=x,则EQ=x,AE=BC=AB=1,∴AQ=1+x,BQ=1-x.
在 Rt △ABQ 中,根据勾股定理,得
解得
特殊平行四边形的折叠问题
1.如图,已知矩形ABCD,将△BCD沿对角线 BD 折叠,记点 C 的对应点为点 C',若 ,则∠BDC 的度数为 ( )
A.55° B.50° C.60° D.65°
2.如图,在菱形纸ABCD中,∠A=60°,点 E 在 BC 边上,将菱形纸片ABCD 沿 DE 折叠,点 C 的对应点为点 C',且 DC'垂直平分AB,则∠DEC的度数为 ( )
A.30° B.45° C.60° D.75°
3.如图,在菱形 ABCD中,∠A =120°,E 是 AD 上的点,沿 BE 折叠△ABE,点 A 恰好落在 BD 上的点 F 处,连接CF,那么∠BFC 的度数是 .
4.如图,在平面直角坐标系中,矩形 ABCO 的边 CO,OA 分别在 x 轴、y轴上,点E 在边 BC 上,将该矩形沿 AE 折叠,点 B 恰好落在边 OC 上的 F 处.若OA = 6,AB = 10, 则点 E 的坐标是 .
5.如图,在正方形ABCD 中,E 是 BC 边上的一点,将正方形边 AB 沿 AE 折叠到 AF,延长 EF交DC 于点G,连接AG,则∠EAG= .
6.如图,在边长为2 的菱形 ABCD 中,∠D =45°,点 E 在 BC 边上,将△ABE沿 AE 所在的直线折叠得到△AB E,AB 交CD 于点 F,且EB 过点 C,则 CB 的长度为 .
7.如图,折叠矩形纸片 ABCD,使点 B 的对应点 E 落在CD边上,GH 为折痕,已知AB=6,BC =10. 当折痕 GH 最长时,线段 BH的长为 .
8.一张矩形纸片ABCD,已知AB=3,AD=2,小明按如图所示的步骤折叠纸片,则四边形 A'EGC'的面积为
9.如图,正方形ABCD中,AB=2,E 为AB 的中点,将△ADE沿DE折叠得到△FDE,且FH⊥BC,垂足为点H,则FH= .
10.如图,在矩形ABCD 中,CD=3,对角线AC =5,点 G,H分别是线段AD,AC上的点,沿 AC 剪开 CH,将△ACD 沿GH 折叠,点 C,D 分别落在点 E,F 处.当点 E落在折线 CAD 上,且 AE = 1 时,CH 的长为 .
11.如图,一张矩形纸片ABCD,将点 B 折叠到对角线AC 上的点M 处,折痕 CE 交 AB 于点 E.将点 D 折叠到对角线 AC 上的点 H 处,折痕 AF 交 DC 于点 F.
(1)求证:AF∥CE.
(2)当∠BAC 的大小为多少度时,四边形AECF 是菱形 请说明理由.
12.(1)问题发现:如图(1),在矩形ABCD 中,点P是边CD 的中点,将△ADP 沿直线AP 折叠后得到△AEP,点 E 在矩形ABCD 内部,延长AE 交 BC 于点 Q,则 EQ 与 CQ 之间的数量关系是 .
(2)拓展探究:如图(2),将(1)中的矩形ABCD改为 ABCD,其他条件不变,请写出 EQ 与 CQ 之间的数量关系,并说明理由.
(3)解决问题:将(1)中的矩形ABCD 改为正方形ABCD,其他条件不变,请直接写出 BQ:CQ 的值.
参考答案
A 由折叠可得∠BDC=∠BDC',∴ ∠ADB =∠BDC'-∠ADC'=∠BDC-20°.
∵ ∠ADB +∠BDC=90°,∴∠BDC-20°+∠BDC=90°,解得∠BDC=55°.
∵四边形ABCD 是矩形.∴ ∠ADC=90°.由折叠可得∠BDC=
2. D 如图,连接BD,AB与DC'的交点记为 P.∵ 四边 形 ABCD 为菱 形,∴AB=AD.∵ ∠A =60°,∴△ABD 为等边三角形,∠ADC = 120°,∠C=60°.∵DC'垂直平分AB,∴∠ADP=∠BDP=30°,∴∠PDC=90°.由折叠可得∠CDE=∠PDE=45°,∴∠DEC=180°-(∠CDE+∠C)=75°.
3.75° ∵四边形ABCD 是菱形,∴AB=BC,∠A +∠ABC=180°,BD 平分∠ABC.∵ ∠A=120°,∴∠ABC=60°,∴∠FBC=30°.根据折叠可得AB=BF,∴FB=BC,∴∠BFC=∠BCF= (180°-30°)=75°.
设CE=a,则BE=6-a,由折叠可知,EF = BE = 6 - a,AF = AB = 10,∴ 在Rt△AOF中, 8,∴CF=OC--OF = 10 - 8 =2.∵ ∠ECF =90°,∴在Rt△CEF中, 解得 点E的坐标是
5.45°∵ 四边形 ABCD 是正方形,∴ AB =AD,
由折叠可知AB =AF,∠ABE = ∠AFE = ∠AFG = 90°,∠BAE = AD=AF,∴ Rt△AGD≌Rt△AGF,∴∠GAF =∠GAD, ∴ ∠EAG = ∠EAF + ∠GAF =
·四边形ABCD 是菱形,∴AB=BC=2,∠B=∠D =45°.∵将△ABE 沿AE 所在的直线折叠得到△AB E,∴BE=B E,AB =AB ,∴∠B =∠B=45°,∴∠BAB =90°,∴BB =
7.6.8 由题意知,当点 E 与点 D 重合时,GH 最长,设BH=x,则 CH =10-x,HE =BH=x.在Rt△HCE 中,由勾股定理得, 即 解得x=6.8.
由折叠可得, 2,A'C'=A'C=3-2=1,∠A'DE=45°,∴C'G=C'D=1,∴ 四边形A'EGC'的面积
如图,过点 F 作MN∥BC,交AB 于点M,交 CD 于点 N. ∵ 四边形ABCD 是正方形,∴ ∠B =∠C= 90°. ∵ MN ∥ BC,∴∠AMF=∠B =90°,∠DNF =∠C = 90°, ∴∠EMF=∠DNF=90°.∵正方形ABCD 中,AB =2,E 为AB的中点,∴ 由折叠得 DF =AD =AB =2,EF= BE = AE = l, ∠A = ∠EFD = 90°,∴∠EFM +∠DFN = ∠DFN + ∠NDF =90°, 设 FH =BM =x,则EM =1-x,FN=2EM =2(1-x) =2-2x,∴ FM =2-FN=2-(2-2x) =2x.在 Rt△EMF 中,由勾股定理得 (2x) ,解得x =0(舍去)
10.2 或
∵在矩形ABCD 中,AC=5. CD=3.∴AD= 当点 E 落在 AC 上时,如图(1),∵ 将△ACD 沿 GH 折叠,∴ CH = EH.∵ AE =1.∴EC=4,∴CH=2.当点 E 落在 AD 上时,如图(2),连接EC.过点E 作 EN⊥AC 于点 将△ACD 沿GH折叠, 综上所述,CH的长为2或
11.(1)证明:∵ 四边形 ABCD 为矩形,
∴AD∥BC,∴∠DAC=∠BCA.
由折叠知
∴∠HAF=∠MCE,∴AF∥CE.
(2)当∠BAC=30°时,四边形AECF 是菱形.理由如下:
∵四边形ABCD 是矩形,
∴∠B=∠BAD=90°,AB∥CD,
由(1)知AF∥CE,
∴ 四边形AECF 是平行四边形.
要使四边形AECF 是菱形,
则AE=EC,即∠EAC=∠ECA.
由折叠可得∠ECA=∠ECB,
∴∠BAC=∠ECA =∠ECB,
∴∠BAC=30°.
12.(1)EQ=CQ
解法提示:连接PQ,
∵点 P为CD的中点,∴ DP=CP.
由折叠的性质可得 DP = PE,∠PEA =∠PDA=90°,
∴PC=PE,∠PCQ=∠PEQ=90°.
∵PQ =PQ,
∴Rt△PEQ≌Rt△PCQ,∴EQ=CQ.
(2)EQ=CQ.
理由:连接EC,
由折叠的性质可知,DP=EP,∠D=∠PEA.
∵点 P是CD的中点,
∴DP=CP,∴EP=CP,
∴ ∠PEC=∠PCE.
∵四边形ABCD 是平行四边形,
∴AD∥BC,∴∠D+∠PCQ=180°.
∵∠PEA+∠PEQ=180°,
∴∠PCQ=∠PEQ.
∴∠PCQ--∠PCE=∠PEQ-∠PEC,
即∠QCE=∠QEC,∴EQ=CQ.
(3)BQ:CQ 的值为3.
解法提示:
设AD=1,CQ=x,则EQ=x,AE=BC=AB=1,∴AQ=1+x,BQ=1-x.
在 Rt △ABQ 中,根据勾股定理,得
解得
同课章节目录
