湖北省黄石八中2024-2025学年上学期12月九年级数学试卷(含答案)
文档属性
| 名称 | 湖北省黄石八中2024-2025学年上学期12月九年级数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-03 19:57:19 | ||
图片预览




文档简介
黄石八中教联体2024 2025学年度上学期12月阶段性教学评价
九年级数学试卷
考试时间:120分钟;满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、选择题(本大题共10个小题,每个题3分,满分30分)
1. 下列方程中,属于一元二次方程的是( )
A B.
C. D.
2. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3. 下列事件是必然事件的是( )
A. 十拿九稳 B. 守株待兔 C. 水中捞月 D. 瓮中捉鳖
4. 下列说法正确的是( )
A. 三点确定一个圆 B. 三角形的外心到三角形三个顶点的距离相等
C. 相等的圆心角所对的弦相等 D. 平分弦的直径垂直于弦.
5. 抛物线的顶点坐标和开口方向分别是( )
A ,开口向上 B. ,开口向下
C. ,开口向上 D. ,开口向下
6. 已知点在反比例函数上的图象上,则m的值为( )
A. B. 3 C. D. 8
7. 有一个人患了流感,经过两轮传染后共有人患了流感,设每轮传染中平均一个人传染了个人,则下列结论不正确的是( )
A. 第一轮后共有个人患了流感
B. 第二轮后又增加个人患流感
C. 依题意可以列方程
D. 按照这样的传染速度,经过三轮传染后共有人患流感
8. 如图,是的内切圆,切点分别为D,E,F,且,,,则的半径是( )
A 1 B. 2 C. D.
9. 我国古代数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.如图,⊙O的半径是2,运用“割圆术”,以圆内接正十二边形面积近似估计⊙O的面积,可得π的估计值是( )
A. 3.1 B. 3 C. 1+ D. 2
10. 如图是二次函数图象的一部分,其对称轴是直线,且过点,有以下结论:①;②;③(m为任意实数);④若方程的两根为,且,则,⑤,其中说法正确的有( )
A. ①②③ B. ②③⑤ C. ②④⑤ D. ②③④⑤
第II卷(非选择题)
二、填空题(本大题共5个小题,每个题3分,满分15分)
11. 点关于原点的对称点的坐标为______.
12. 已知点都在反比例函数(a为常数)的图象上,且,则的大小关系为______(用“”连接).
13. 如图,的半径为2,圆心P在函数的图象上运动,当与坐标轴相切时,点P的坐标为______.
14. 如图,圆锥底面圆的半径r为,沿一条母线将圆锥侧面剪开并展平,得到一个圆心角θ为的扇形,则圆锥的侧面积为______.(用含的式子表示)
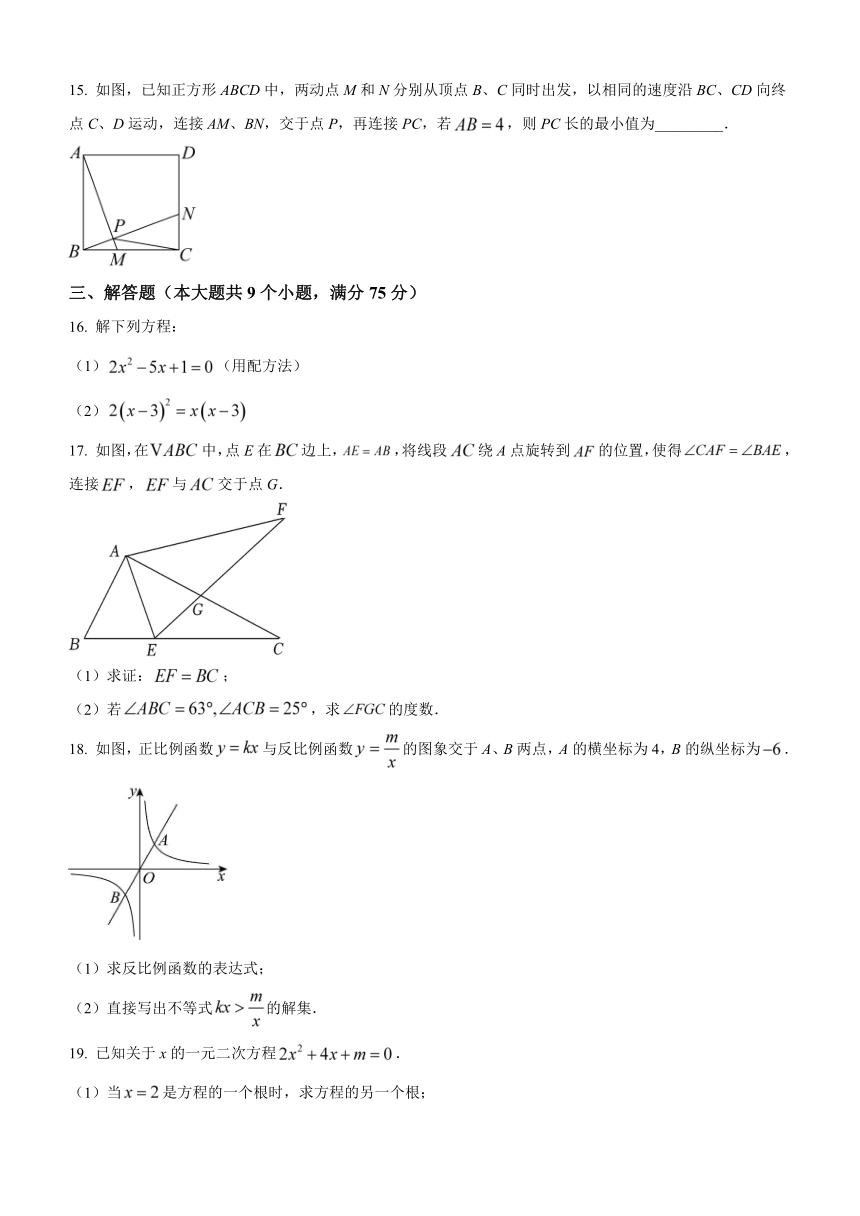
15. 如图,已知正方形ABCD中,两动点M和N分别从顶点B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,再连接PC,若,则PC长的最小值为_________.
三、解答题(本大题共9个小题,满分75分)
16. 解下列方程:
(1)(用配方法)
(2)
17. 如图,在中,点E在边上,,将线段绕A点旋转到的位置,使得,连接,与交于点G.
(1)求证:;
(2)若,求的度数.
18. 如图,正比例函数与反比例函数的图象交于A、B两点,A的横坐标为4,B的纵坐标为.
(1)求反比例函数的表达式;
(2)直接写出不等式的解集.
19. 已知关于x的一元二次方程.
(1)当是方程的一个根时,求方程的另一个根;
(2)若,是方程的两个不相等的实根,且,满足,求m的值.
20. 为了建设书香校园,更好地满足学生的阅读需求,某校决定新增四类书籍(科普类、文学类、艺术类、工具类),并计划根据学生的需求情况进行采购.为此,学校随机抽取了部分学生进行调查(每名学生必选且只选一类图书),并将调查结果进行统计分析,绘制成如下不完整的统计图.
根据以上信息,解答下列问题:
(1)选文学类图书的学生有_____人, _____°;
(2)若该校共有学生1800人,请估计该校学生中需要工具类图书的人数;
(3)某班计划从报名的甲、乙、丙、丁四名学生中随机选择两名学生作为班级图书管理员,请用列表或画树状图的方法,求同时选中乙和丙的概率.
21. 如图,在中,,O为上一点,以O为圆心,为半径作交于另一点D,E为上一点,且.
(1)判断与的位置关系,说明理由;
(2)若,,,求长.
22. 某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量y(千克)与销售价格x(元/千克)()存在一次函数关系,部分数据如表所示:
销售价格x(元/千克) 50 40
日销售量y(千克) 100 200
(1)试求出y关于x的函数表达式.
(2)设该经销商销售这种淡水鱼的日销售利润为W元,如果不考虑其他因素,求当销售价格x为多少时,日销售利润W最大?最大的日销售利润是多少元?
(3)请直接写出当利润大于0且不超过2000元时销售价格x的取值范围.
23 综合与实践
(1)问题初探
如图1,在中,为边上的中线,求的取值范围.请直接写出的取值范围.
(2)问题解决
如图2,P为等边三角形内一点,满足,试求的大小.
(3)问题拓展
如图3,在正方形中,分别为边上的点,满足,若,求证的面积.
24. 已知抛物线与轴交于、两点,与轴交于点,其对称轴为.
(1)求抛物线的表达式;
(2)如图1,点是对称轴上的一动点,连接、,当最小时,求点的坐标;
(3)如图2,作直线,动点在轴上方的抛物线上(不与点重合),过点作直线的垂线,交直线与点,设点的横坐标为,.试求出关于的函数解析式,并根据的不同取值,探索点的个数情况.
九年级数学参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D B A A D B B B
11.
12.
13.或
14.3πcm2/3π平方厘米
15.
16.(1)x1= +, x2= - + ;
(2)x1=3, x2=6
17.
(1)证明:∵,
∴.
∵将线段绕A点旋转到的位置,
∴.
在与中,
,
∴,
∴;
(2)解:∵,
∴,
∴,
∴.
∵,
∴,
∴.
18.(1)解:∵正比例函数与反比例函数的图象交于两点,
∴、关于原点对称,
∴,
把代入可得:,
∴;
(2)解:由图象可知,不等式的解集是或.
19.
(1)解:设另一个根为,则,
解得
∴另一个根为;
(2)解:由题意得:,
同时满足即,
∴,
∵,.
∴
∴,
解得,
∴的值为.
20.
(1)调查的学生总人数为(人),
∴选文学类图书的学生有(人).
.
故答案为:70,108;
(2)(人),
∴估计该校学生中需要工具类图书的人数约180人.
(3)列表如下:
甲 乙 丙 丁
甲 (甲,乙) (甲,丙) (甲,丁)
乙 (乙,甲) (乙,丙) (乙,丁)
丙 (丙,甲) (丙,乙) (丙,丁)
丁 (丁,甲) (丁,乙) (丁,丙)
共有12种等可能的结果,其中同时选中乙和丙的结果有:(乙,丙),(丙,乙),共2种,
∴同时选中乙和丙的概率为.
21.
(1)解:是的切线;理由如下:
连接,如图1,
,
,
,
,
又,
,
,
,
是圆的半径,
是的切线;
(2)连接,,如图2,
,,
,
,
,
设,则,
,
由勾股定理得:,,
,
,
.
22.
(1)解:设关于的函数表达式为.
将,和,分别代入,得:,
解得:,
关于的函数表达式是:;
(2)解:.
当时,在的范围内,取到最大值,最大值是2250.
答:销售价格为每千克45元时,日销售利润最大,最大日销售利润是2250元;
(3)解:解方程,
整理得,
即,
解得,,
当时,解得或;
∵的对称轴为直线,且,
∴当或时,利润大于0且不超过2000元,
答:当利润大于0且不超过2000元时销售价格x的取值范围是或.
23.
(1)解:如图,将绕点D旋转,得到,连接,
由旋转,,
∴四边形是平行四边形,
,,
又,
,
得,
即,
;
(2)如图,将绕点B顺时针旋转得到,连接,
由旋转可知,,
,
是等边三角形,
,
在中,
,,
,
,
,
,
(3)将绕点A顺时针旋转得到,
由旋转可知,,
,
,
,
,
,
在与中,
,
,,
.
24.
(1)解:抛物线与y轴交于点,
∴,
∵对称轴为,
∴,,
∴抛物线的解析式为;
(2)由题意可知,B点关于对称轴的对称的点为A(-4,0)直线AC的解析式为y=x+4,当x= - 时,y=,所以D( -,)
九年级数学试卷
考试时间:120分钟;满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、选择题(本大题共10个小题,每个题3分,满分30分)
1. 下列方程中,属于一元二次方程的是( )
A B.
C. D.
2. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3. 下列事件是必然事件的是( )
A. 十拿九稳 B. 守株待兔 C. 水中捞月 D. 瓮中捉鳖
4. 下列说法正确的是( )
A. 三点确定一个圆 B. 三角形的外心到三角形三个顶点的距离相等
C. 相等的圆心角所对的弦相等 D. 平分弦的直径垂直于弦.
5. 抛物线的顶点坐标和开口方向分别是( )
A ,开口向上 B. ,开口向下
C. ,开口向上 D. ,开口向下
6. 已知点在反比例函数上的图象上,则m的值为( )
A. B. 3 C. D. 8
7. 有一个人患了流感,经过两轮传染后共有人患了流感,设每轮传染中平均一个人传染了个人,则下列结论不正确的是( )
A. 第一轮后共有个人患了流感
B. 第二轮后又增加个人患流感
C. 依题意可以列方程
D. 按照这样的传染速度,经过三轮传染后共有人患流感
8. 如图,是的内切圆,切点分别为D,E,F,且,,,则的半径是( )
A 1 B. 2 C. D.
9. 我国古代数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.如图,⊙O的半径是2,运用“割圆术”,以圆内接正十二边形面积近似估计⊙O的面积,可得π的估计值是( )
A. 3.1 B. 3 C. 1+ D. 2
10. 如图是二次函数图象的一部分,其对称轴是直线,且过点,有以下结论:①;②;③(m为任意实数);④若方程的两根为,且,则,⑤,其中说法正确的有( )
A. ①②③ B. ②③⑤ C. ②④⑤ D. ②③④⑤
第II卷(非选择题)
二、填空题(本大题共5个小题,每个题3分,满分15分)
11. 点关于原点的对称点的坐标为______.
12. 已知点都在反比例函数(a为常数)的图象上,且,则的大小关系为______(用“”连接).
13. 如图,的半径为2,圆心P在函数的图象上运动,当与坐标轴相切时,点P的坐标为______.
14. 如图,圆锥底面圆的半径r为,沿一条母线将圆锥侧面剪开并展平,得到一个圆心角θ为的扇形,则圆锥的侧面积为______.(用含的式子表示)
15. 如图,已知正方形ABCD中,两动点M和N分别从顶点B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,再连接PC,若,则PC长的最小值为_________.
三、解答题(本大题共9个小题,满分75分)
16. 解下列方程:
(1)(用配方法)
(2)
17. 如图,在中,点E在边上,,将线段绕A点旋转到的位置,使得,连接,与交于点G.
(1)求证:;
(2)若,求的度数.
18. 如图,正比例函数与反比例函数的图象交于A、B两点,A的横坐标为4,B的纵坐标为.
(1)求反比例函数的表达式;
(2)直接写出不等式的解集.
19. 已知关于x的一元二次方程.
(1)当是方程的一个根时,求方程的另一个根;
(2)若,是方程的两个不相等的实根,且,满足,求m的值.
20. 为了建设书香校园,更好地满足学生的阅读需求,某校决定新增四类书籍(科普类、文学类、艺术类、工具类),并计划根据学生的需求情况进行采购.为此,学校随机抽取了部分学生进行调查(每名学生必选且只选一类图书),并将调查结果进行统计分析,绘制成如下不完整的统计图.
根据以上信息,解答下列问题:
(1)选文学类图书的学生有_____人, _____°;
(2)若该校共有学生1800人,请估计该校学生中需要工具类图书的人数;
(3)某班计划从报名的甲、乙、丙、丁四名学生中随机选择两名学生作为班级图书管理员,请用列表或画树状图的方法,求同时选中乙和丙的概率.
21. 如图,在中,,O为上一点,以O为圆心,为半径作交于另一点D,E为上一点,且.
(1)判断与的位置关系,说明理由;
(2)若,,,求长.
22. 某水产经销商以每千克30元的价格购进一批某品种淡水鱼,由销售经验可知,这种淡水鱼的日销售量y(千克)与销售价格x(元/千克)()存在一次函数关系,部分数据如表所示:
销售价格x(元/千克) 50 40
日销售量y(千克) 100 200
(1)试求出y关于x的函数表达式.
(2)设该经销商销售这种淡水鱼的日销售利润为W元,如果不考虑其他因素,求当销售价格x为多少时,日销售利润W最大?最大的日销售利润是多少元?
(3)请直接写出当利润大于0且不超过2000元时销售价格x的取值范围.
23 综合与实践
(1)问题初探
如图1,在中,为边上的中线,求的取值范围.请直接写出的取值范围.
(2)问题解决
如图2,P为等边三角形内一点,满足,试求的大小.
(3)问题拓展
如图3,在正方形中,分别为边上的点,满足,若,求证的面积.
24. 已知抛物线与轴交于、两点,与轴交于点,其对称轴为.
(1)求抛物线的表达式;
(2)如图1,点是对称轴上的一动点,连接、,当最小时,求点的坐标;
(3)如图2,作直线,动点在轴上方的抛物线上(不与点重合),过点作直线的垂线,交直线与点,设点的横坐标为,.试求出关于的函数解析式,并根据的不同取值,探索点的个数情况.
九年级数学参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D B A A D B B B
11.
12.
13.或
14.3πcm2/3π平方厘米
15.
16.(1)x1= +, x2= - + ;
(2)x1=3, x2=6
17.
(1)证明:∵,
∴.
∵将线段绕A点旋转到的位置,
∴.
在与中,
,
∴,
∴;
(2)解:∵,
∴,
∴,
∴.
∵,
∴,
∴.
18.(1)解:∵正比例函数与反比例函数的图象交于两点,
∴、关于原点对称,
∴,
把代入可得:,
∴;
(2)解:由图象可知,不等式的解集是或.
19.
(1)解:设另一个根为,则,
解得
∴另一个根为;
(2)解:由题意得:,
同时满足即,
∴,
∵,.
∴
∴,
解得,
∴的值为.
20.
(1)调查的学生总人数为(人),
∴选文学类图书的学生有(人).
.
故答案为:70,108;
(2)(人),
∴估计该校学生中需要工具类图书的人数约180人.
(3)列表如下:
甲 乙 丙 丁
甲 (甲,乙) (甲,丙) (甲,丁)
乙 (乙,甲) (乙,丙) (乙,丁)
丙 (丙,甲) (丙,乙) (丙,丁)
丁 (丁,甲) (丁,乙) (丁,丙)
共有12种等可能的结果,其中同时选中乙和丙的结果有:(乙,丙),(丙,乙),共2种,
∴同时选中乙和丙的概率为.
21.
(1)解:是的切线;理由如下:
连接,如图1,
,
,
,
,
又,
,
,
,
是圆的半径,
是的切线;
(2)连接,,如图2,
,,
,
,
,
设,则,
,
由勾股定理得:,,
,
,
.
22.
(1)解:设关于的函数表达式为.
将,和,分别代入,得:,
解得:,
关于的函数表达式是:;
(2)解:.
当时,在的范围内,取到最大值,最大值是2250.
答:销售价格为每千克45元时,日销售利润最大,最大日销售利润是2250元;
(3)解:解方程,
整理得,
即,
解得,,
当时,解得或;
∵的对称轴为直线,且,
∴当或时,利润大于0且不超过2000元,
答:当利润大于0且不超过2000元时销售价格x的取值范围是或.
23.
(1)解:如图,将绕点D旋转,得到,连接,
由旋转,,
∴四边形是平行四边形,
,,
又,
,
得,
即,
;
(2)如图,将绕点B顺时针旋转得到,连接,
由旋转可知,,
,
是等边三角形,
,
在中,
,,
,
,
,
,
(3)将绕点A顺时针旋转得到,
由旋转可知,,
,
,
,
,
,
在与中,
,
,,
.
24.
(1)解:抛物线与y轴交于点,
∴,
∵对称轴为,
∴,,
∴抛物线的解析式为;
(2)由题意可知,B点关于对称轴的对称的点为A(-4,0)直线AC的解析式为y=x+4,当x= - 时,y=,所以D( -,)
同课章节目录
