1.2.2直角三角形的性质和判定 教案
文档属性
| 名称 | 1.2.2直角三角形的性质和判定 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 275.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 20:18:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
分课时教学设计
第4课时《1.2.2直角三角形的性质和判》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 体会从“一般到特殊”的思维方法和“逆向思维”方法,培养逆向思维能力.
学习者分析 发展有条理思考和有条理表达的能力,通过实际问题的解决让学生体会数学的应用价值.
教学目标 运用勾股定理及直角三角形的判定条件解决实际问题. 2.培养“逆向思维”方法及逆向思维能力.
教学重点 能运用勾股定理及直角三角形的判定条件解决实际问题.
教学难点 能运用勾股定理及直角三角形的判定条件解决实际问题.
学习活动设计
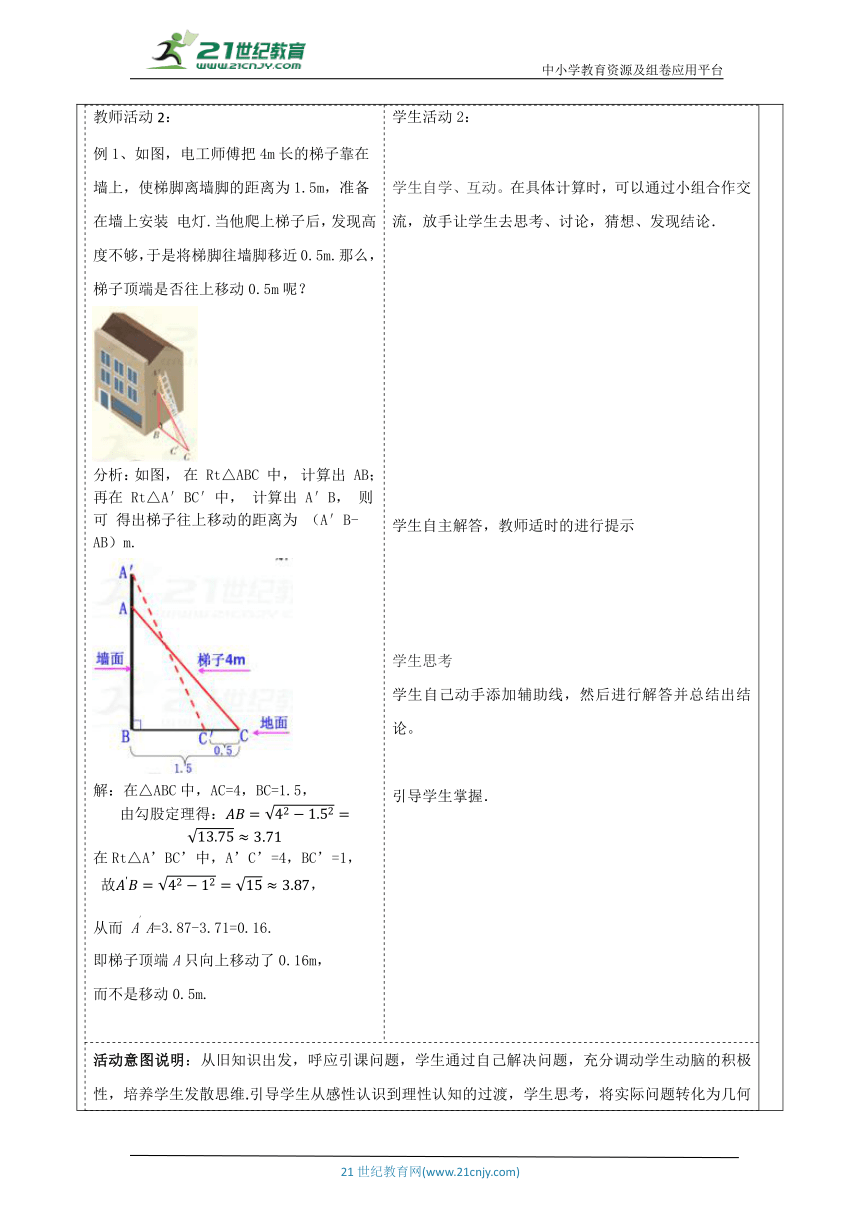
教师活动学生活动环节一:引入新课复习引入 如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1m为2步) 这种做法不可取学生活动1: 学生在教师的引导下,能很快回忆相关问题. ? 活动意图说明:激发学生兴趣,引入新课主题,通过观察图片,来引出新知识.培养学生爱护环境的意识,激发学生的兴趣,理解学生思考,进行探索. 环节二:新知探究教师活动2: 例1、如图,电工师傅把4m长的梯子靠在墙上,使梯脚离墙脚的距离为1.5m,准备在墙上安装 电灯.当他爬上梯子后,发现高度不够,于是将梯脚往墙脚移近0.5m.那么,梯子顶端是否往上移动0.5m呢? 分析:如图, 在 Rt△ABC 中, 计算出 AB; 再在 Rt△A′BC′中, 计算出 A′B, 则可 得出梯子往上移动的距离为 (A′B- AB)m. 解:在△ABC中,AC=4,BC=1.5, 由勾股定理得: 在Rt△A’BC’中,A’C’=4,BC’=1, 故, 从而 A′A=3.87-3.71=0.16. 即梯子顶端A只向上移动了0.16m, 而不是移动0.5m. 学生活动2: 学生自学、互动。在具体计算时,可以通过小组合作交流,放手让学生去思考、讨论,猜想、发现结论. 学生自主解答,教师适时的进行提示 学生思考 学生自己动手添加辅助线,然后进行解答并总结出结论。 引导学生掌握.活动意图说明:从旧知识出发,呼应引课问题,学生通过自己解决问题,充分调动学生动脑的积极性,培养学生发散思维.引导学生从感性认识到理性认知的过渡,学生思考,将实际问题转化为几何问题. 环节三:典例精析 例2、“引葭(jia)赴岸”是《九章算术》中一道题“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?” 题意是:有一个边长为10尺的正方形池塘,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好到达岸边.请问这个水池的深度和这根芦苇的长度各是多少? 学生活动3: 参与教师分析和讲例题. 在学生自主、合作、探究后,学生解答,师生归纳出 活动意图说明:熟练掌握.巩固学的知识,学生通过自己解决问题,充分发挥学习的主动性,通过此题的解答,使学生对知识的掌握进一步的提高,使学生对知识的掌握进一步的提高.?
板书设计
课堂练习 【知识技能类作业】 必做题: 1.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( ). A.12米 B.13 米 C.14米 D.15米 2、如图,一架云梯长10米,斜靠在一面墙上,梯子顶端离地面6米,要使梯子顶端离地面8米,则梯子的底部在水平面方向要向左滑动_____米. 选做题: 3、如图,某人欲垂直横渡一条河,由于水流的影响,他实际上岸地点C偏离了想要达到的B点140米,(即BC=140米),其结果是他在水中实际游了500米(即AC=500米),求该河AB处的宽度. 【综合拓展类作业】 4.为了丰富少年儿童的业余文化生活,某社区在如图9所示AB所在的直线上建一图书阅览室,本社区有两所学校所在的位置在点C和D处.CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:阅览室E应建在距A多少㎞处,才能使它到C、D两所学校的距离相等?
课堂总结
作业设计 【知识技能类作业】 必做题: 1.一个木工师傅测量了一个等腰三角形的腰、底边和高的长,但他把这三个数据与其它的数据弄混了,请你帮助他找出来,是第( )组. A.13,12,12 B.12,12,8 C.13,10,12 D.5,8,4 选做题: 2.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB. 【综合拓展类作业】 3.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B,蚂蚁沿着圆柱侧面爬行的最短路程是多少?(π取3)
教学反思 勾股定理的应用 将实际问题转化为数学问题,建立数学模型 运用勾股定理解决生活中的一些实际问题
21世纪教育网(www.21cnjy.com)
分课时教学设计
第4课时《1.2.2直角三角形的性质和判》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 体会从“一般到特殊”的思维方法和“逆向思维”方法,培养逆向思维能力.
学习者分析 发展有条理思考和有条理表达的能力,通过实际问题的解决让学生体会数学的应用价值.
教学目标 运用勾股定理及直角三角形的判定条件解决实际问题. 2.培养“逆向思维”方法及逆向思维能力.
教学重点 能运用勾股定理及直角三角形的判定条件解决实际问题.
教学难点 能运用勾股定理及直角三角形的判定条件解决实际问题.
学习活动设计
教师活动学生活动环节一:引入新课复习引入 如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1m为2步) 这种做法不可取学生活动1: 学生在教师的引导下,能很快回忆相关问题. ? 活动意图说明:激发学生兴趣,引入新课主题,通过观察图片,来引出新知识.培养学生爱护环境的意识,激发学生的兴趣,理解学生思考,进行探索. 环节二:新知探究教师活动2: 例1、如图,电工师傅把4m长的梯子靠在墙上,使梯脚离墙脚的距离为1.5m,准备在墙上安装 电灯.当他爬上梯子后,发现高度不够,于是将梯脚往墙脚移近0.5m.那么,梯子顶端是否往上移动0.5m呢? 分析:如图, 在 Rt△ABC 中, 计算出 AB; 再在 Rt△A′BC′中, 计算出 A′B, 则可 得出梯子往上移动的距离为 (A′B- AB)m. 解:在△ABC中,AC=4,BC=1.5, 由勾股定理得: 在Rt△A’BC’中,A’C’=4,BC’=1, 故, 从而 A′A=3.87-3.71=0.16. 即梯子顶端A只向上移动了0.16m, 而不是移动0.5m. 学生活动2: 学生自学、互动。在具体计算时,可以通过小组合作交流,放手让学生去思考、讨论,猜想、发现结论. 学生自主解答,教师适时的进行提示 学生思考 学生自己动手添加辅助线,然后进行解答并总结出结论。 引导学生掌握.活动意图说明:从旧知识出发,呼应引课问题,学生通过自己解决问题,充分调动学生动脑的积极性,培养学生发散思维.引导学生从感性认识到理性认知的过渡,学生思考,将实际问题转化为几何问题. 环节三:典例精析 例2、“引葭(jia)赴岸”是《九章算术》中一道题“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?” 题意是:有一个边长为10尺的正方形池塘,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好到达岸边.请问这个水池的深度和这根芦苇的长度各是多少? 学生活动3: 参与教师分析和讲例题. 在学生自主、合作、探究后,学生解答,师生归纳出 活动意图说明:熟练掌握.巩固学的知识,学生通过自己解决问题,充分发挥学习的主动性,通过此题的解答,使学生对知识的掌握进一步的提高,使学生对知识的掌握进一步的提高.?
板书设计
课堂练习 【知识技能类作业】 必做题: 1.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( ). A.12米 B.13 米 C.14米 D.15米 2、如图,一架云梯长10米,斜靠在一面墙上,梯子顶端离地面6米,要使梯子顶端离地面8米,则梯子的底部在水平面方向要向左滑动_____米. 选做题: 3、如图,某人欲垂直横渡一条河,由于水流的影响,他实际上岸地点C偏离了想要达到的B点140米,(即BC=140米),其结果是他在水中实际游了500米(即AC=500米),求该河AB处的宽度. 【综合拓展类作业】 4.为了丰富少年儿童的业余文化生活,某社区在如图9所示AB所在的直线上建一图书阅览室,本社区有两所学校所在的位置在点C和D处.CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:阅览室E应建在距A多少㎞处,才能使它到C、D两所学校的距离相等?
课堂总结
作业设计 【知识技能类作业】 必做题: 1.一个木工师傅测量了一个等腰三角形的腰、底边和高的长,但他把这三个数据与其它的数据弄混了,请你帮助他找出来,是第( )组. A.13,12,12 B.12,12,8 C.13,10,12 D.5,8,4 选做题: 2.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB. 【综合拓展类作业】 3.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B,蚂蚁沿着圆柱侧面爬行的最短路程是多少?(π取3)
教学反思 勾股定理的应用 将实际问题转化为数学问题,建立数学模型 运用勾股定理解决生活中的一些实际问题
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
