1.2.2直角三角形的性质和判定 课件(共20张PPT)
文档属性
| 名称 | 1.2.2直角三角形的性质和判定 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 20:20:34 | ||
图片预览




文档简介
(共20张PPT)
第一章 直角三角形
1.2.2直角三角形的性质和判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
经历探索勾股定理及验证勾股定理的过程。
02
新知导入
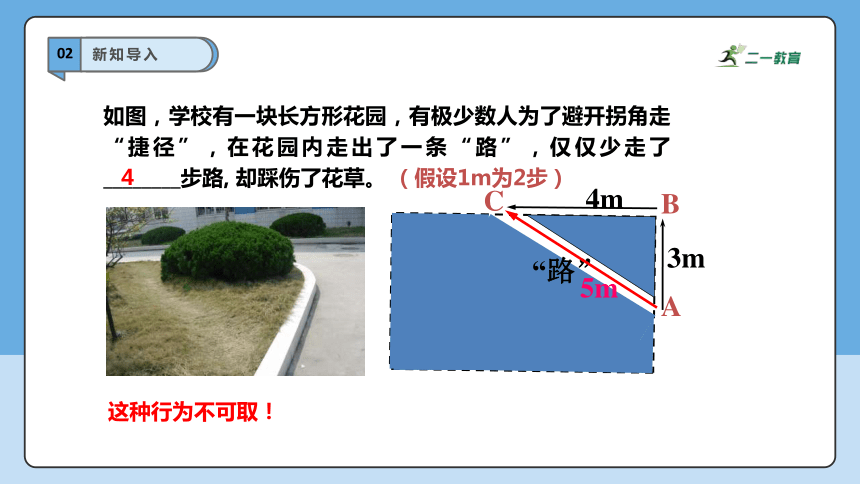
如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1m为2步)
3m
4m
“路”
A
B
C
5m
4
这种行为不可取!
新课探究
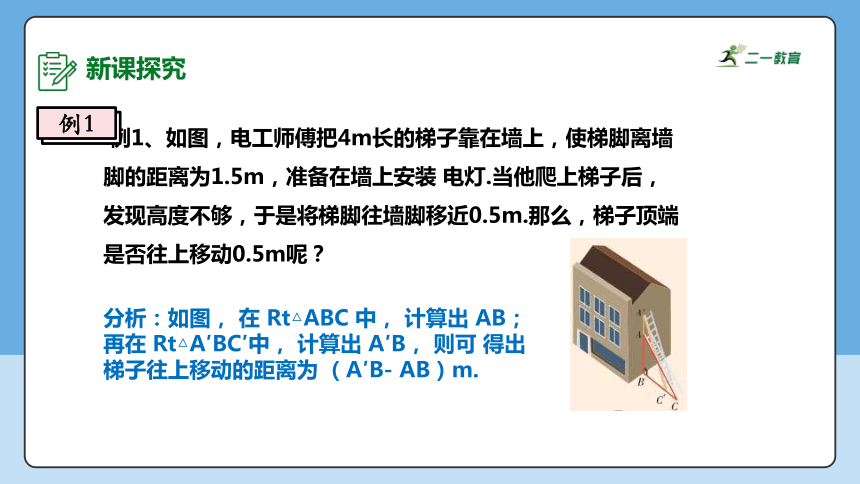
例1、如图,电工师傅把4m长的梯子靠在墙上,使梯脚离墙脚的距离为1.5m,准备在墙上安装 电灯.当他爬上梯子后,发现高度不够,于是将梯脚往墙脚移近0.5m.那么,梯子顶端是否往上移动0.5m呢?
分析:如图, 在 Rt△ABC 中, 计算出 AB; 再在 Rt△A′BC′中, 计算出 A′B, 则可 得出梯子往上移动的距离为 (A′B- AB)m.
例1
03
新知探究
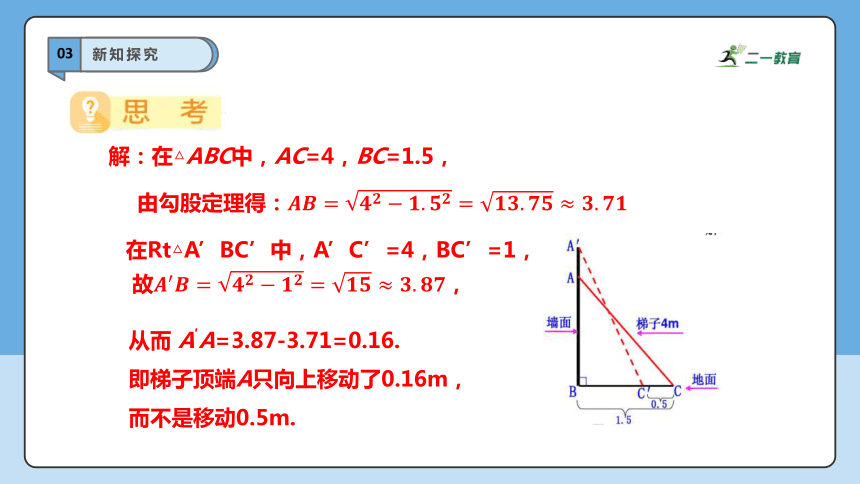
解:在△ABC中,AC=4,BC=1.5,
由勾股定理得:
在Rt△A’BC’中,A’C’=4,BC’=1,
故,
从而 A′A=3.87-3.71=0.16.
即梯子顶端A只向上移动了0.16m,
而不是移动0.5m.
03
新知讲解
例2
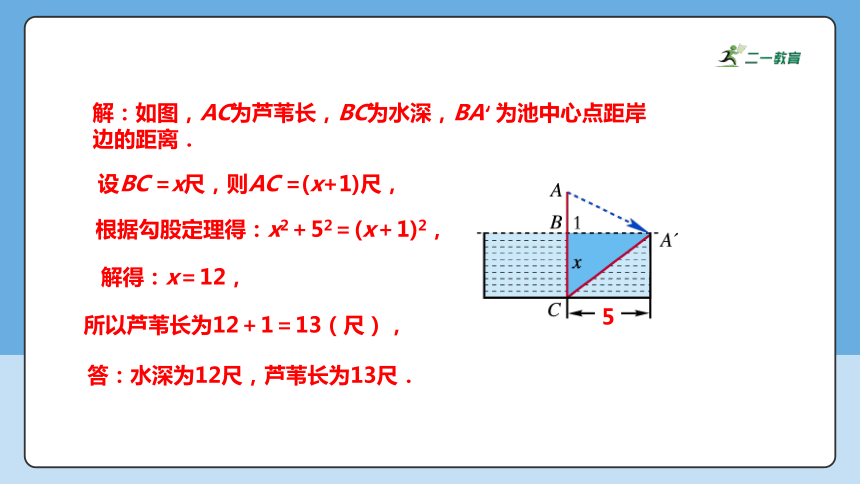
例2、“引葭(jia)赴岸”是《九章算术》中一道题“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”
题意是:有一个边长为10尺的正方形池塘,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好到达岸边.请问这个水池的深度和这根芦苇的长度各是多少?
5
解:如图,AC为芦苇长,BC为水深,BA 为池中心点距岸边的距离.
设BC =x尺,则AC =(x+1)尺,
根据勾股定理得:x2+52=(x+1)2,
解得:x=12,
答:水深为12尺,芦苇长为13尺.
5
所以芦苇长为12+1=13(尺),
04
课堂练习
【知识技能类作业】必做题:
1.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( ).
A.12米 B.13 米 C.14米 D.15米
A
2、如图,一架云梯长10米,斜靠在一面墙上,梯子顶端离地面6米,要使梯子顶端离地面8米,则梯子的底部在水平面方向要向左滑动_____米.
20
04
课堂练习
【知识技能类作业】选做题:
3、如图,某人欲垂直横渡一条河,由于水流的影响,他实际上岸地点C偏离了想要达到的B点140米,(即BC=140米),其结果是他在水中实际游了500米(即AC=500米),求该河AB处的宽度.
解:在Rt△ABC中,AB2+BC2=AC2,
所以AB2+1402=5002,
解得AB=480.
答:该河AB处的宽度为480米。
04
课堂练习
【综合拓展类作业】
4、为了丰富少年儿童的业余文化生活,某社区在如图9所示AB所在的直线上建一图书阅览室,本社区有两所学校所在的位置在点C和D处.CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:阅览室E应建在距A多少㎞处,才能使它到C、D两所学校的距离相等?
04
课堂练习
【综合拓展类作业】
解:设阅览室E到A的距离为x㎞.连结CE、DE.
在Rt△EAC和Rt△EBD中,CE2=AE2+AC2=x2+152,
DE2=EB2+DB2=(25-x)2+102.
因为点E到点CD的距离,
所以CE=DE.所以CE2=DE2.
即x2+152=(25-x)2+102.所以x=10.
因此,阅览室E应建在距A10km处.
05
课堂小结
直角三角形的性质与判定
(1)将实际问题转化为数学问题,建立数学模型
(2)运用勾股定理解决生活中的一些实际问题.
勾股定理的应用
06
作业布置
【知识技能类作业】必做题:
1.一个木工师傅测量了一个等腰三角形的腰、底边和高的长,但他把这三个数据与其它的数据弄混了,请你帮助他找出来,是第( )组.
A.13,12,12 B.12,12,8 C.13,10,12 D.5,8,4
C
06
作业布置
【知识技能类作业】选做题:
2.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB.
解:设AD=x米,则AB为(10+x)米,AC为(15-x)米,BC为5米,
∴(x+10)2+52=(15-x)2,解得x=2,
∴10+x=12(米)
答:树高12米
06
作业布置
【综合拓展类作业】
3.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B,蚂蚁沿着圆柱侧面爬行的最短路程是多少?(π取3)
06
作业布置
【综合拓展类作业】
分析:因为两点之间线段最短,所以可以将圆柱的侧面展开,再求出线段AB的长即为蚂蚁的最短路。
解:∵
∴
答:蚂蚁爬行的最短路程是15厘米
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.2.2直角三角形的性质和判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
经历探索勾股定理及验证勾股定理的过程。
02
新知导入
如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1m为2步)
3m
4m
“路”
A
B
C
5m
4
这种行为不可取!
新课探究
例1、如图,电工师傅把4m长的梯子靠在墙上,使梯脚离墙脚的距离为1.5m,准备在墙上安装 电灯.当他爬上梯子后,发现高度不够,于是将梯脚往墙脚移近0.5m.那么,梯子顶端是否往上移动0.5m呢?
分析:如图, 在 Rt△ABC 中, 计算出 AB; 再在 Rt△A′BC′中, 计算出 A′B, 则可 得出梯子往上移动的距离为 (A′B- AB)m.
例1
03
新知探究
解:在△ABC中,AC=4,BC=1.5,
由勾股定理得:
在Rt△A’BC’中,A’C’=4,BC’=1,
故,
从而 A′A=3.87-3.71=0.16.
即梯子顶端A只向上移动了0.16m,
而不是移动0.5m.
03
新知讲解
例2
例2、“引葭(jia)赴岸”是《九章算术》中一道题“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”
题意是:有一个边长为10尺的正方形池塘,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好到达岸边.请问这个水池的深度和这根芦苇的长度各是多少?
5
解:如图,AC为芦苇长,BC为水深,BA 为池中心点距岸边的距离.
设BC =x尺,则AC =(x+1)尺,
根据勾股定理得:x2+52=(x+1)2,
解得:x=12,
答:水深为12尺,芦苇长为13尺.
5
所以芦苇长为12+1=13(尺),
04
课堂练习
【知识技能类作业】必做题:
1.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( ).
A.12米 B.13 米 C.14米 D.15米
A
2、如图,一架云梯长10米,斜靠在一面墙上,梯子顶端离地面6米,要使梯子顶端离地面8米,则梯子的底部在水平面方向要向左滑动_____米.
20
04
课堂练习
【知识技能类作业】选做题:
3、如图,某人欲垂直横渡一条河,由于水流的影响,他实际上岸地点C偏离了想要达到的B点140米,(即BC=140米),其结果是他在水中实际游了500米(即AC=500米),求该河AB处的宽度.
解:在Rt△ABC中,AB2+BC2=AC2,
所以AB2+1402=5002,
解得AB=480.
答:该河AB处的宽度为480米。
04
课堂练习
【综合拓展类作业】
4、为了丰富少年儿童的业余文化生活,某社区在如图9所示AB所在的直线上建一图书阅览室,本社区有两所学校所在的位置在点C和D处.CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:阅览室E应建在距A多少㎞处,才能使它到C、D两所学校的距离相等?
04
课堂练习
【综合拓展类作业】
解:设阅览室E到A的距离为x㎞.连结CE、DE.
在Rt△EAC和Rt△EBD中,CE2=AE2+AC2=x2+152,
DE2=EB2+DB2=(25-x)2+102.
因为点E到点CD的距离,
所以CE=DE.所以CE2=DE2.
即x2+152=(25-x)2+102.所以x=10.
因此,阅览室E应建在距A10km处.
05
课堂小结
直角三角形的性质与判定
(1)将实际问题转化为数学问题,建立数学模型
(2)运用勾股定理解决生活中的一些实际问题.
勾股定理的应用
06
作业布置
【知识技能类作业】必做题:
1.一个木工师傅测量了一个等腰三角形的腰、底边和高的长,但他把这三个数据与其它的数据弄混了,请你帮助他找出来,是第( )组.
A.13,12,12 B.12,12,8 C.13,10,12 D.5,8,4
C
06
作业布置
【知识技能类作业】选做题:
2.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB.
解:设AD=x米,则AB为(10+x)米,AC为(15-x)米,BC为5米,
∴(x+10)2+52=(15-x)2,解得x=2,
∴10+x=12(米)
答:树高12米
06
作业布置
【综合拓展类作业】
3.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B,蚂蚁沿着圆柱侧面爬行的最短路程是多少?(π取3)
06
作业布置
【综合拓展类作业】
分析:因为两点之间线段最短,所以可以将圆柱的侧面展开,再求出线段AB的长即为蚂蚁的最短路。
解:∵
∴
答:蚂蚁爬行的最短路程是15厘米
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
