北师大版九年级下册1.1.1锐角三角函数-正切 教案(表格式)
文档属性
| 名称 | 北师大版九年级下册1.1.1锐角三角函数-正切 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 218.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-03 00:00:00 | ||
图片预览

文档简介
课 题 §1.1.1锐角三角函数——正切 日期
教学目标 经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系. 能够用tan A表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算. 3.学习用数形结合的思想分析问题和解决问题,提高解决实际问题的能力.
教材分析 重点 理解正切、倾斜程度、坡度的数学意义
难点 理解正切的意义,并用它来表示两边之比,刻画梯子的陡缓程度
教学、学法 精讲精练
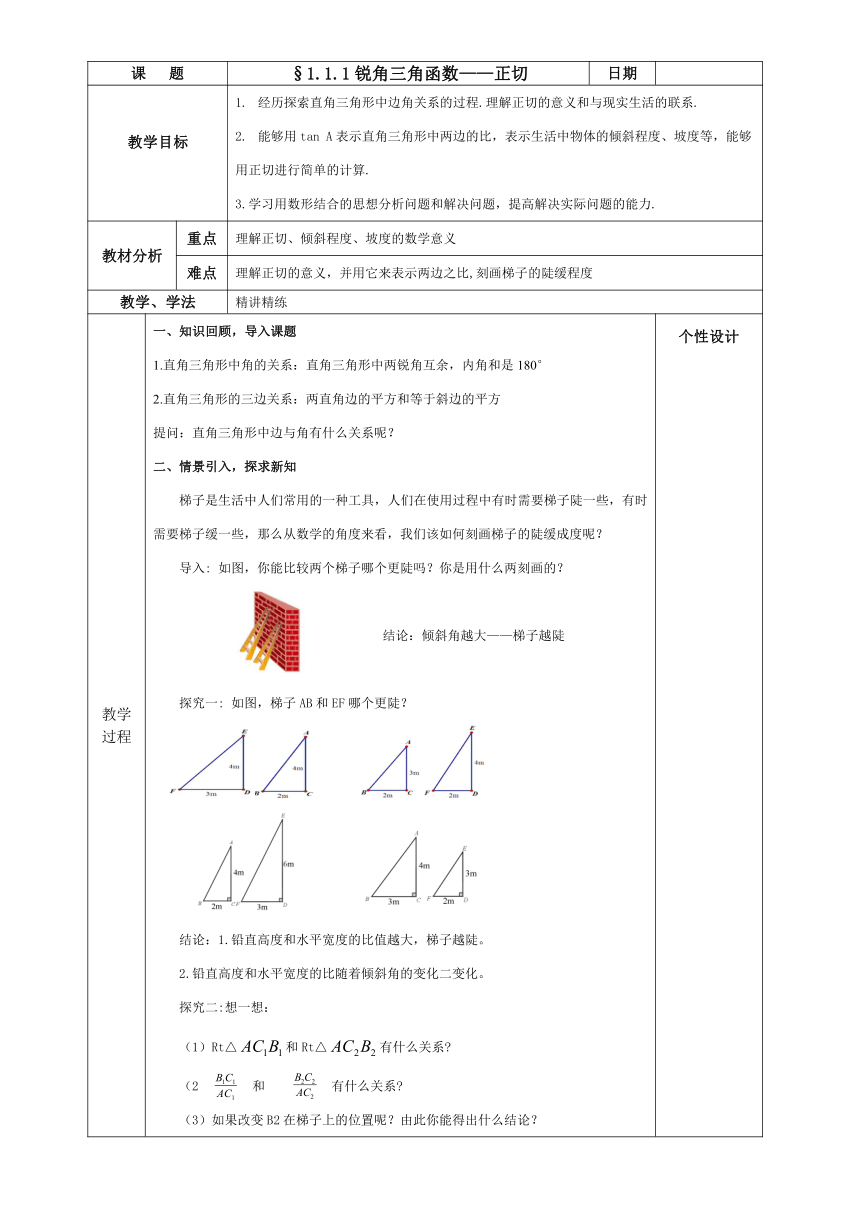
教学过程 一、知识回顾,导入课题 1.直角三角形中角的关系:直角三角形中两锐角互余,内角和是180° 2.直角三角形的三边关系:两直角边的平方和等于斜边的平方 提问:直角三角形中边与角有什么关系呢? 情景引入,探求新知 梯子是生活中人们常用的一种工具,人们在使用过程中有时需要梯子陡一些,有时需要梯子缓一些,那么从数学的角度来看,我们该如何刻画梯子的陡缓成度呢? 导入: 如图,你能比较两个梯子哪个更陡吗?你是用什么两刻画的? 结论:倾斜角越大——梯子越陡 探究一: 如图,梯子AB和EF哪个更陡? 结论:1.铅直高度和水平宽度的比值越大,梯子越陡。 2.铅直高度和水平宽度的比随着倾斜角的变化二变化。 探究二:想一想: Rt△和Rt△有什么关系 和 有什么关系 (3)如果改变B2在梯子上的位置呢?由此你能得出什么结论? 结论:∠A的大小确定, ∠A的对边与邻边的比值不变. 正切定义:在Rt△ABC中,锐角A对边与邻边的比随之确定 , 这个比叫做∠A的正切(tangent).记作tanA.即: 例2、已知Rt△ABC中,∠C=90°,BC=8,AB=10,求tanA 变式练习:在Rt△ABC中,∠C=90°,AC=6,tanB=,求AB. 2.坡度与坡角 (1)坡面与水平面的夹角(α)叫坡角. (2)坡面的铅直高度与水平宽度的比称为坡度 (或坡比),即坡度等于坡角的正切. 例3、某人沿一斜坡的底端B走了10米到达点A,此时点A到地面BC的垂直高度AC为6米,则斜坡AB的坡度为多少? 三、随堂检测,巩固提升 例2.如图,拦水坝的坡度为 1:,若坝高BC=20米,求AC,AB. 已知Rt△ABC中,∠C=90°,BC=8,AB=10,求tanA. 变式1.已知:Rt△ABC中,∠C=90°,tanB=3/4 ,AC=6,求AB. 变式2.已知:Rt△ABC中,AC=BC,BD=AB,求∠1的正切值。 四、课堂练习 随堂练习,习题1.1第1,2题 五、课堂小结,内化所学 今天你学到了哪些知识?掌握了哪些数学思想方法? 个性设计
板书设计 锐角三角函数——正切 正切的定义 梯子的陡峭程度与正切值的关系 坡角与坡度
作业布置 书面 校本 A、B
拓展 校本C
教学反思 教案检查记录
签字
教学目标 经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系. 能够用tan A表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算. 3.学习用数形结合的思想分析问题和解决问题,提高解决实际问题的能力.
教材分析 重点 理解正切、倾斜程度、坡度的数学意义
难点 理解正切的意义,并用它来表示两边之比,刻画梯子的陡缓程度
教学、学法 精讲精练
教学过程 一、知识回顾,导入课题 1.直角三角形中角的关系:直角三角形中两锐角互余,内角和是180° 2.直角三角形的三边关系:两直角边的平方和等于斜边的平方 提问:直角三角形中边与角有什么关系呢? 情景引入,探求新知 梯子是生活中人们常用的一种工具,人们在使用过程中有时需要梯子陡一些,有时需要梯子缓一些,那么从数学的角度来看,我们该如何刻画梯子的陡缓成度呢? 导入: 如图,你能比较两个梯子哪个更陡吗?你是用什么两刻画的? 结论:倾斜角越大——梯子越陡 探究一: 如图,梯子AB和EF哪个更陡? 结论:1.铅直高度和水平宽度的比值越大,梯子越陡。 2.铅直高度和水平宽度的比随着倾斜角的变化二变化。 探究二:想一想: Rt△和Rt△有什么关系 和 有什么关系 (3)如果改变B2在梯子上的位置呢?由此你能得出什么结论? 结论:∠A的大小确定, ∠A的对边与邻边的比值不变. 正切定义:在Rt△ABC中,锐角A对边与邻边的比随之确定 , 这个比叫做∠A的正切(tangent).记作tanA.即: 例2、已知Rt△ABC中,∠C=90°,BC=8,AB=10,求tanA 变式练习:在Rt△ABC中,∠C=90°,AC=6,tanB=,求AB. 2.坡度与坡角 (1)坡面与水平面的夹角(α)叫坡角. (2)坡面的铅直高度与水平宽度的比称为坡度 (或坡比),即坡度等于坡角的正切. 例3、某人沿一斜坡的底端B走了10米到达点A,此时点A到地面BC的垂直高度AC为6米,则斜坡AB的坡度为多少? 三、随堂检测,巩固提升 例2.如图,拦水坝的坡度为 1:,若坝高BC=20米,求AC,AB. 已知Rt△ABC中,∠C=90°,BC=8,AB=10,求tanA. 变式1.已知:Rt△ABC中,∠C=90°,tanB=3/4 ,AC=6,求AB. 变式2.已知:Rt△ABC中,AC=BC,BD=AB,求∠1的正切值。 四、课堂练习 随堂练习,习题1.1第1,2题 五、课堂小结,内化所学 今天你学到了哪些知识?掌握了哪些数学思想方法? 个性设计
板书设计 锐角三角函数——正切 正切的定义 梯子的陡峭程度与正切值的关系 坡角与坡度
作业布置 书面 校本 A、B
拓展 校本C
教学反思 教案检查记录
签字
