课时7.2.3平行线的性质 课件(共24张PPT)2024-2025七年级下册数学人教(2024)版
文档属性
| 名称 | 课时7.2.3平行线的性质 课件(共24张PPT)2024-2025七年级下册数学人教(2024)版 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-20 10:18:24 | ||
图片预览






文档简介
(共24张PPT)
7.2.3 平行线的性质
任课教师:XXX
班级:XX年XX班
第7章 相交线与平行线
学习目标
1.学生能够准确识别同位角、内错角、同旁内角等与平行线判定相关的角关系。
2.熟练掌握“同位角相等,两直线平行”“内错角相等,两直线平行““同旁内角互补,两直线平行“这三种平行线的判定方法,并能准确运用这些方法判断两条直线是否平行。
3.经历观察、操作、想象、推理等活动过程,提高空间观念和逻辑推理能力。
4.通过对不同图形中角与直线关系的分析,培养分析问题和解决问题的能力,学会从复杂图形中抽象出基本的角与直线关系用于判定平行。
目录
贰
内容教学
叁
例题讲解
肆
课后作业
壹
复习导入
复习引入
复习引入
从上节课内容我们学会了平行线的判定;
① ,两直线平行;
② ,两直线平行;
③ ,两直线平行;
那么如果两条直线平行,我们能得到什么?
同位角相等
内错角相等
同旁内角互补
内容教学
内容教学
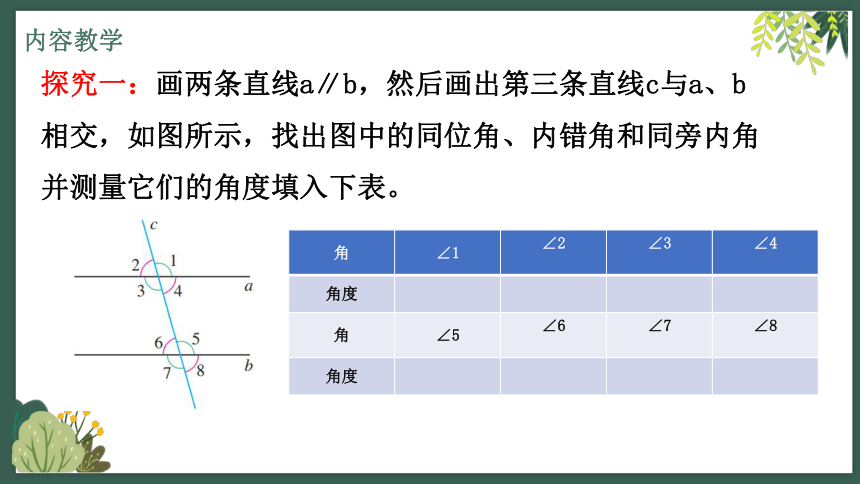
探究一:画两条直线a∥b,然后画出第三条直线c与a、b相交,如图所示,找出图中的同位角、内错角和同旁内角并测量它们的角度填入下表。
角 ∠1 ∠2 ∠3 ∠4
角度
角 ∠5 ∠6 ∠7 ∠8
角度
内容教学
观察与猜想:两条平行线被第三条直线所截,得到的各对同位角之间有什么关系?说出你的猜想。
猜想:两直线平行,同位角 。
试一试:在任意画一条直线与a、b相交,同样测量各个角的度数,看上述猜想是否还成立?
相等
性质1:两条平行线被第三条直线所截,同位角相等。
内容教学
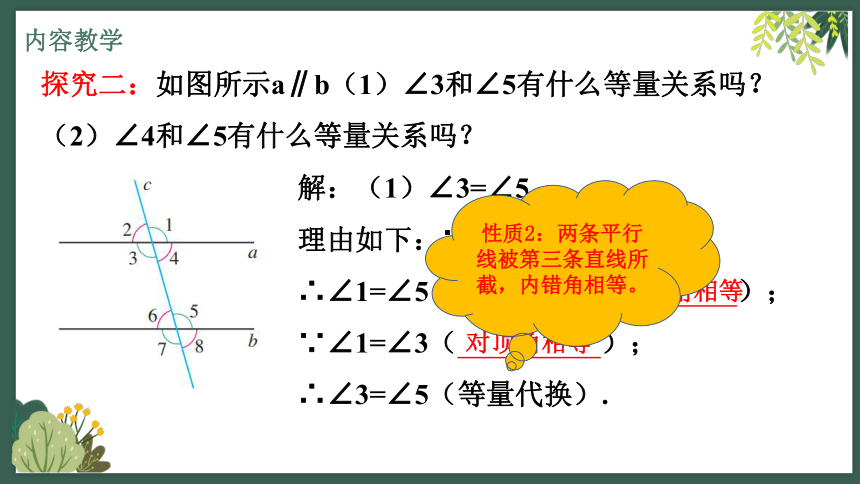
探究二:如图所示a∥b(1)∠3和∠5有什么等量关系吗?(2)∠4和∠5有什么等量关系吗?
解:(1)∠3=∠5
理由如下:∵a∥b(已知);
∴∠1=∠5( , );
∵∠1=∠3( );
∴∠3=∠5(等量代换).
两直线平行
同位角相等
对顶角相等
性质2:两条平行线被第三条直线所截,内错角相等。
内容教学
探究二:如图所示a∥b(1)∠3和∠5有什么等量关系吗?(2)∠4和∠5有什么等量关系吗?。
(2)∠4+∠5=180°
理由如下:∵∠1+∠4=180°∠1=∠5
∴∠5+∠4=180°
性质3:两条平行线被第三条直线所截,同旁内角互补。
例题讲解
例题讲解
例1 完成下列证明.
已知:如图AB∥CD,∠A=∠C,求证:BC∥AD
证明:∵AB∥CD(已知),
∴∠ABE=∠______( )
∵∠A=∠C(已知),
∴∠ABE=∠_____( ),
∴BC∥AD( )
C
两直线平行,同位角相等
A
等量代换
内错角相等,两直线平行
例题讲解
例2 如图所示是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角∠D、∠C分别是多少度?
解:因为梯形上、下两底 DC与AB 互相平行,根据“两直线平行,同旁内角互补”,可得∠A与
∠D 互补,∠B与∠C互补.于是
∠D=180°-∠A =180°-100°=80°
∠C=180°-∠B =180°-115°=65°
所以梯形的另外两个角∠D,∠C分别是80°,65°。
课堂练习
1.如图,直线a、b被直线c所截,且a∥b,若∠1=45°,则∠2的度数为( )
A
A.45° B.115° C. 125° D.135°
课堂练习
2.如图,AD是△ABC的角平分线,DE∥AC,交AB于点E,DF∥AB,交AC于点G,若∠1=50°,则的度数为( )
C
A.40° B.45° C. 50° D.60°
课堂练习
3.将一副三角板的直角顶点重合按如图放置,小明得到下列结论:①如果∠2=30°,则AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则∠2=30°.其中正确的结论有( )
B
A.1个 B.2个 C.3个 D.0个
课堂练习
4.如图∠ABC=90°,∠C=60°,过点B作DE∥AC.则∠ABD的度数是 .
30°
A.a B.b C.m D.n
课堂练习
5.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=21°,∠FED=45°,则∠GFH的度数为 .
24°
课堂练习
6.如图,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2.求证:(1)AB∥CD;
证明:∵BE、DF分别平分∠ABC、∠ADC,∴∠3=∠ADC=∠ABC
∵∠ADC=∠ABC,∴∠1=∠3
∵∠1=∠2,∴∠2=∠3
∴AB∥CD
课堂练习
6.如图,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2.求证:(2)∠A=∠C;
证明∵AB∥CD
∴∠A+ADC=180°,∠ABC+∠C=180°
∵∠ADC=∠ABC,
∴∠A=∠C
课堂练习
7.在横线上填上合适的答案,在括号内填上恰当的依据.如图所示,E为线段DF上的点,B为线段AC上的点,∠1=∠2,∠C=∠D.求证:DF∥AC.
证明:∵∠1=∠2(已知),∠1=∠3( ),
∴∠2=∠3( ),
∴______∥_____( ).
∴∠C=∠ABD( ).
∵∠C=∠D( ).
∴∠ABD=∠D( ).
∴DF∥AC( ).
对顶角相等
等量代换
CE
BD
同位角相等,两直线平行
两直线平行,同位角相等
已知
等量代换
内错角相等,两直线平行
课后作业布置
ENTER YOUR TITLE
课后作业布置
作业参考本书籍作业分层
感谢各位同学观看
TO FEEL THE FLAME OF DREAMING AND TO FEEL THE MOMENT OFDANCING,
WHEN ALL THE ROMANCE IS FAR AWAY,THE ETERNITY IS ALWAYS THERE.
任课教师:XXX
班级:XX年XX班
7.2.3 平行线的性质
任课教师:XXX
班级:XX年XX班
第7章 相交线与平行线
学习目标
1.学生能够准确识别同位角、内错角、同旁内角等与平行线判定相关的角关系。
2.熟练掌握“同位角相等,两直线平行”“内错角相等,两直线平行““同旁内角互补,两直线平行“这三种平行线的判定方法,并能准确运用这些方法判断两条直线是否平行。
3.经历观察、操作、想象、推理等活动过程,提高空间观念和逻辑推理能力。
4.通过对不同图形中角与直线关系的分析,培养分析问题和解决问题的能力,学会从复杂图形中抽象出基本的角与直线关系用于判定平行。
目录
贰
内容教学
叁
例题讲解
肆
课后作业
壹
复习导入
复习引入
复习引入
从上节课内容我们学会了平行线的判定;
① ,两直线平行;
② ,两直线平行;
③ ,两直线平行;
那么如果两条直线平行,我们能得到什么?
同位角相等
内错角相等
同旁内角互补
内容教学
内容教学
探究一:画两条直线a∥b,然后画出第三条直线c与a、b相交,如图所示,找出图中的同位角、内错角和同旁内角并测量它们的角度填入下表。
角 ∠1 ∠2 ∠3 ∠4
角度
角 ∠5 ∠6 ∠7 ∠8
角度
内容教学
观察与猜想:两条平行线被第三条直线所截,得到的各对同位角之间有什么关系?说出你的猜想。
猜想:两直线平行,同位角 。
试一试:在任意画一条直线与a、b相交,同样测量各个角的度数,看上述猜想是否还成立?
相等
性质1:两条平行线被第三条直线所截,同位角相等。
内容教学
探究二:如图所示a∥b(1)∠3和∠5有什么等量关系吗?(2)∠4和∠5有什么等量关系吗?
解:(1)∠3=∠5
理由如下:∵a∥b(已知);
∴∠1=∠5( , );
∵∠1=∠3( );
∴∠3=∠5(等量代换).
两直线平行
同位角相等
对顶角相等
性质2:两条平行线被第三条直线所截,内错角相等。
内容教学
探究二:如图所示a∥b(1)∠3和∠5有什么等量关系吗?(2)∠4和∠5有什么等量关系吗?。
(2)∠4+∠5=180°
理由如下:∵∠1+∠4=180°∠1=∠5
∴∠5+∠4=180°
性质3:两条平行线被第三条直线所截,同旁内角互补。
例题讲解
例题讲解
例1 完成下列证明.
已知:如图AB∥CD,∠A=∠C,求证:BC∥AD
证明:∵AB∥CD(已知),
∴∠ABE=∠______( )
∵∠A=∠C(已知),
∴∠ABE=∠_____( ),
∴BC∥AD( )
C
两直线平行,同位角相等
A
等量代换
内错角相等,两直线平行
例题讲解
例2 如图所示是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角∠D、∠C分别是多少度?
解:因为梯形上、下两底 DC与AB 互相平行,根据“两直线平行,同旁内角互补”,可得∠A与
∠D 互补,∠B与∠C互补.于是
∠D=180°-∠A =180°-100°=80°
∠C=180°-∠B =180°-115°=65°
所以梯形的另外两个角∠D,∠C分别是80°,65°。
课堂练习
1.如图,直线a、b被直线c所截,且a∥b,若∠1=45°,则∠2的度数为( )
A
A.45° B.115° C. 125° D.135°
课堂练习
2.如图,AD是△ABC的角平分线,DE∥AC,交AB于点E,DF∥AB,交AC于点G,若∠1=50°,则的度数为( )
C
A.40° B.45° C. 50° D.60°
课堂练习
3.将一副三角板的直角顶点重合按如图放置,小明得到下列结论:①如果∠2=30°,则AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则∠2=30°.其中正确的结论有( )
B
A.1个 B.2个 C.3个 D.0个
课堂练习
4.如图∠ABC=90°,∠C=60°,过点B作DE∥AC.则∠ABD的度数是 .
30°
A.a B.b C.m D.n
课堂练习
5.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=21°,∠FED=45°,则∠GFH的度数为 .
24°
课堂练习
6.如图,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2.求证:(1)AB∥CD;
证明:∵BE、DF分别平分∠ABC、∠ADC,∴∠3=∠ADC=∠ABC
∵∠ADC=∠ABC,∴∠1=∠3
∵∠1=∠2,∴∠2=∠3
∴AB∥CD
课堂练习
6.如图,∠ADC=∠ABC,BE、DF分别平分∠ABC、∠ADC,且∠1=∠2.求证:(2)∠A=∠C;
证明∵AB∥CD
∴∠A+ADC=180°,∠ABC+∠C=180°
∵∠ADC=∠ABC,
∴∠A=∠C
课堂练习
7.在横线上填上合适的答案,在括号内填上恰当的依据.如图所示,E为线段DF上的点,B为线段AC上的点,∠1=∠2,∠C=∠D.求证:DF∥AC.
证明:∵∠1=∠2(已知),∠1=∠3( ),
∴∠2=∠3( ),
∴______∥_____( ).
∴∠C=∠ABD( ).
∵∠C=∠D( ).
∴∠ABD=∠D( ).
∴DF∥AC( ).
对顶角相等
等量代换
CE
BD
同位角相等,两直线平行
两直线平行,同位角相等
已知
等量代换
内错角相等,两直线平行
课后作业布置
ENTER YOUR TITLE
课后作业布置
作业参考本书籍作业分层
感谢各位同学观看
TO FEEL THE FLAME OF DREAMING AND TO FEEL THE MOMENT OFDANCING,
WHEN ALL THE ROMANCE IS FAR AWAY,THE ETERNITY IS ALWAYS THERE.
任课教师:XXX
班级:XX年XX班
同课章节目录
