山东省德州市夏津县双语中学2016届九年级下学期第一次检测数学试题
文档属性
| 名称 | 山东省德州市夏津县双语中学2016届九年级下学期第一次检测数学试题 | 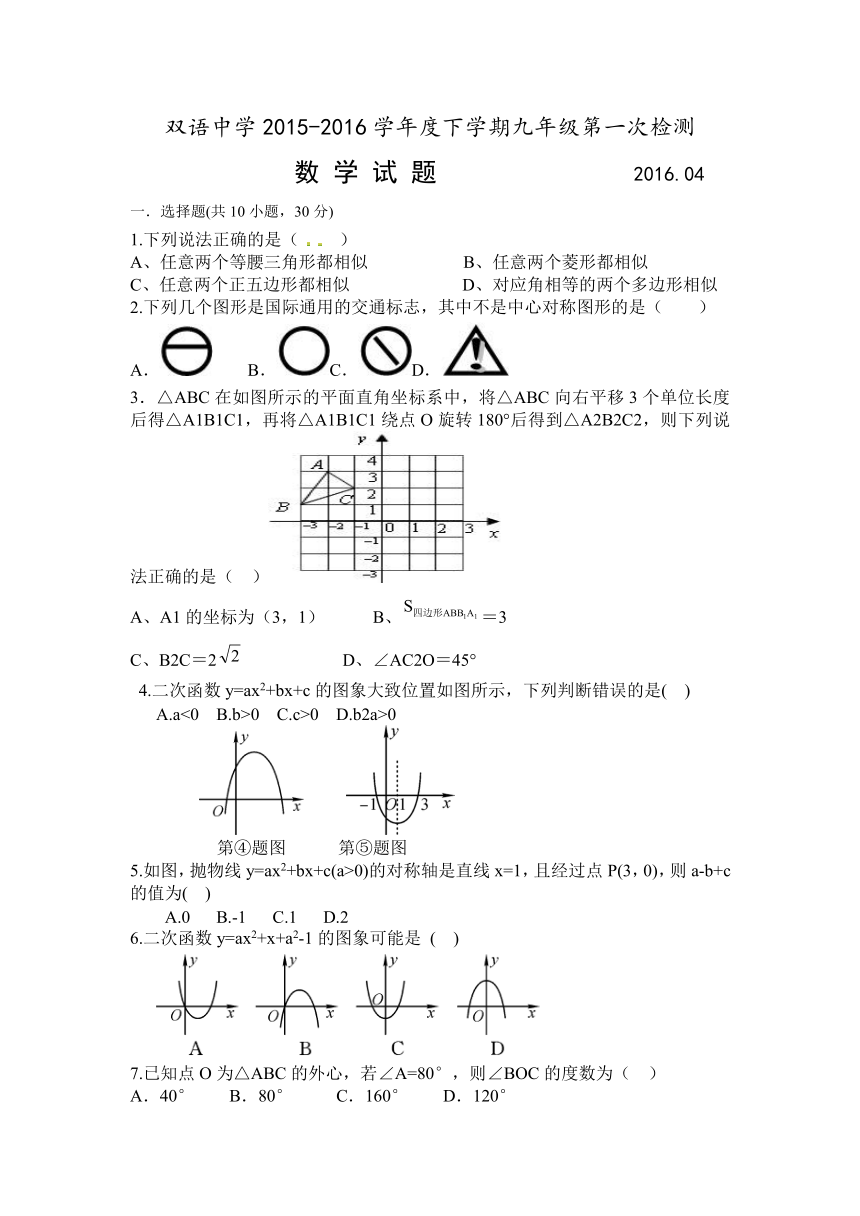 | |
| 格式 | zip | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-13 13:54:31 | ||
图片预览


文档简介
双语中学2015-2016学年度下学期九年级第一次检测
数 学 试 题 2016.04
一.选择题(共10小题,30分)
1.下列说法正确的是( )
A、任意两个等腰三角形都相似 B、任意两个菱形都相似
C、任意两个正五边形都相似 D、对应角相等的两个多边形相似
2.下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )
A.B.C.D.
3.△ABC在如图所示的平面直角坐标系中,将△ABC向右平移3个单位长度后得△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2,则下列说法正确的是( )
A、A1的坐标为(3,1) B、=3
C、B2C=2 D、∠AC2O=45°
4.二次函数y=ax2+bx+c的图象大致位置如图所示,下列判断错误的是( )
A.a<0 B.b>0 C.c>0 D.b2a>0
第④题图 第⑤题图
5.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为( )
A.0 B.-1 C.1 D.2
6.二次函数y=ax2+x+a2-1的图象可能是 ( )
7.已知点O为△ABC的外心,若∠A=80°,则∠BOC的度数为( )
A.40° B.80° C.160° D.120°
8. 已知在△ABC中,AB=AC=13,BC=10,那么△ABC的内切圆的半径为( )
A. B. C.2 D.3
9.甲、乙、丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲、乙各比赛了4局,丙当了3次裁判.问第2局的输者是( )
A.甲 B.乙 C.丙 D.不能确定
10.已知反比例函数的图象上有两点A(x1,y1)、B(x2,y2),若y1>y2,则x1﹣x2的值是( )
A. 正数 B. 负数 C. 非正数 D. 不能确定
二填空题(共4小题,16分)
11.在Rt△ABC中,∠C=90゜,AC=5,BC=12,以C为圆心,R为半径作圆与斜边AB相切,则R的值为__________。
12.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为__________。
13.已知扇形的周长为20cm,面积为16cm2,那么扇形的半径为__________。
14.在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是_______.
三.解答题(共6小题,74分)
15.已知二次函数的图象经过点A(3,0),B(2,-3),C(0,-3),求函数的解析式和对称轴.
16.如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1。
(1)线段OA1的长是________,∠AOB1的度数是________。
(2)连接AA1,求证:四边形OAA1B1是平行四边形。
(3)求四边形OAA1B1的面积。
17.如图,已知⊙O的半径为8cm,点A为半径OB的延长线上一点,射线AC切⊙O于点C,BC的长为,求线段AB的长。
18、如图,在△ABC中,∠C=120°,AC=BC,AB=4,半圆的圆心O在AB上,且与AC,BC分别相切于点D,E。(1)求半圆O的半径。(2)求图中阴影部分的面积。
19.如图,一次函数y=kx+b的图象与坐标轴分别交于A.B两点,与反比例函数y=的图象在第二象限的交点为C,CD⊥x轴,垂足为D.若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例函数的解析式;
(2)直接写出当x<0时,kx+b->0的解集.
20.点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
九年级数学答案
1-10CDDDABCACD
11.
60
13
12.2或8.13.1.6cm 14. >2.
15.解:设函数解析式为y=ax2+bx+c,因为二次函数的图象经过点A(3,0),B(2,-3),C(0,-3),则有解得
∴函数的解析式为y=x2-2x-3,其对称轴为直线x=1.
16.
因为,∠OAB=90°,OA=AB,
所以,△OAB为等腰直角三角形,即∠AOB=45°,
根据旋转的性质,对应点到旋转中心的距离相等,即OA1=OA=6,
对应角∠A1OB1=∠AOB=45°,旋转角∠AOA1=90°,
所以,∠AOB1的度数是90°+45°=135°.
(2)∵∠AOA1=∠OA1B1=90°,
∴OA∥A1B1,
又OA=AB=A1B1,
∴四边形OAA1B1是平行四边形.
(3) OAA1B1的面积=6×6=36.
17.解:设∠AOC=,∵BC的长为,∴,解得。
∵AC为⊙O的切线,∴△AOC为直角三角形,∴OA=2OC=16cm,∴AB=OA-OB=8cm。
18.
(1)连结OD,OC,
∵半圆与AC,BC分别相切于点D,E
∴,且,
∵,
∴且O是AB的中点,
∴,
∵,
∴,
∴,
∴在中,,即半圆的半径为1。
(2)设CO=x,则在,因为,所以AC=2x,由勾股定理得: ,
即,解得(舍去)
∴,
∵半圆的半径为1,
∴半圆的面积为,
∴。
19.解:(1)∵OB=2,△AOB的面积为1,
∴B(﹣2,0),OA=1,
∴A(0,﹣1),
∴ , ∴,
∴y=﹣x﹣1;
又∵OD=4,OD⊥x轴,
∴C(﹣4,y),将x=﹣4代入y=﹣x﹣1,得y=1,
∴C(﹣4,1)
∴1=,
∴m=﹣4,
∴y=﹣;
(2)当x<0时,kx+b﹣>0的解集是x<﹣4.
20.(1)OA绕点O顺时针旋转120°至OB的位置.做BD垂直y轴
则OB与y轴夹角为30°
则在△OBD中 OB=4 BD=2 OD=2√3
则点B坐标为(-2,-2√3)
(2)抛物线方程y=ax +bx+c
已知点B(-2,-2√3) O(0,0) A(4,0)
代入方程解得
a=-√3/6
b=2√3/3
c=0
则抛物线方程y=(-√3/6)x +(2√3/3)x
(3)若△POB为等腰三角形
则过P做OB的中垂线PE垂足为E
OB的直线方程为y=√3x 则垂直于OB直线斜率为k=-1/√3
设直线PE为 y=kx+m
已知斜率为k=-1/√3,过E点(-1,-√3) 【OB中点】
解得m=-4√3/3
直线PE y=- √3x/3-4√3/3
联立直线、抛物线方程y=(-√3/6)x +(2√3/3)x
y=- √3x/3-4√3/3
的x -6x-8=0 二元一次方程根 x={-b±√(b2-4ac)}/2a
X1=3+√17 X2=3-√17
有根即存在点P
代入X1,X2
解得Y1=-(7√3/3+√51/3 ) Y2=-(7√3/3-√51/3 )
点P坐标P1(3+√17,-7√3/3-√51/3 ) P2(3-√17,-7√3/3+√51/3)
⌒
数 学 试 题 2016.04
一.选择题(共10小题,30分)
1.下列说法正确的是( )
A、任意两个等腰三角形都相似 B、任意两个菱形都相似
C、任意两个正五边形都相似 D、对应角相等的两个多边形相似
2.下列几个图形是国际通用的交通标志,其中不是中心对称图形的是( )
A.B.C.D.
3.△ABC在如图所示的平面直角坐标系中,将△ABC向右平移3个单位长度后得△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2,则下列说法正确的是( )
A、A1的坐标为(3,1) B、=3
C、B2C=2 D、∠AC2O=45°
4.二次函数y=ax2+bx+c的图象大致位置如图所示,下列判断错误的是( )
A.a<0 B.b>0 C.c>0 D.b2a>0
第④题图 第⑤题图
5.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为( )
A.0 B.-1 C.1 D.2
6.二次函数y=ax2+x+a2-1的图象可能是 ( )
7.已知点O为△ABC的外心,若∠A=80°,则∠BOC的度数为( )
A.40° B.80° C.160° D.120°
8. 已知在△ABC中,AB=AC=13,BC=10,那么△ABC的内切圆的半径为( )
A. B. C.2 D.3
9.甲、乙、丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲、乙各比赛了4局,丙当了3次裁判.问第2局的输者是( )
A.甲 B.乙 C.丙 D.不能确定
10.已知反比例函数的图象上有两点A(x1,y1)、B(x2,y2),若y1>y2,则x1﹣x2的值是( )
A. 正数 B. 负数 C. 非正数 D. 不能确定
二填空题(共4小题,16分)
11.在Rt△ABC中,∠C=90゜,AC=5,BC=12,以C为圆心,R为半径作圆与斜边AB相切,则R的值为__________。
12.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为__________。
13.已知扇形的周长为20cm,面积为16cm2,那么扇形的半径为__________。
14.在平面直角坐标系中,点P(m,m-2)在第一象限内,则m的取值范围是_______.
三.解答题(共6小题,74分)
15.已知二次函数的图象经过点A(3,0),B(2,-3),C(0,-3),求函数的解析式和对称轴.
16.如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1。
(1)线段OA1的长是________,∠AOB1的度数是________。
(2)连接AA1,求证:四边形OAA1B1是平行四边形。
(3)求四边形OAA1B1的面积。
17.如图,已知⊙O的半径为8cm,点A为半径OB的延长线上一点,射线AC切⊙O于点C,BC的长为,求线段AB的长。
18、如图,在△ABC中,∠C=120°,AC=BC,AB=4,半圆的圆心O在AB上,且与AC,BC分别相切于点D,E。(1)求半圆O的半径。(2)求图中阴影部分的面积。
19.如图,一次函数y=kx+b的图象与坐标轴分别交于A.B两点,与反比例函数y=的图象在第二象限的交点为C,CD⊥x轴,垂足为D.若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例函数的解析式;
(2)直接写出当x<0时,kx+b->0的解集.
20.点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
九年级数学答案
1-10CDDDABCACD
11.
60
13
12.2或8.13.1.6cm 14. >2.
15.解:设函数解析式为y=ax2+bx+c,因为二次函数的图象经过点A(3,0),B(2,-3),C(0,-3),则有解得
∴函数的解析式为y=x2-2x-3,其对称轴为直线x=1.
16.
因为,∠OAB=90°,OA=AB,
所以,△OAB为等腰直角三角形,即∠AOB=45°,
根据旋转的性质,对应点到旋转中心的距离相等,即OA1=OA=6,
对应角∠A1OB1=∠AOB=45°,旋转角∠AOA1=90°,
所以,∠AOB1的度数是90°+45°=135°.
(2)∵∠AOA1=∠OA1B1=90°,
∴OA∥A1B1,
又OA=AB=A1B1,
∴四边形OAA1B1是平行四边形.
(3) OAA1B1的面积=6×6=36.
17.解:设∠AOC=,∵BC的长为,∴,解得。
∵AC为⊙O的切线,∴△AOC为直角三角形,∴OA=2OC=16cm,∴AB=OA-OB=8cm。
18.
(1)连结OD,OC,
∵半圆与AC,BC分别相切于点D,E
∴,且,
∵,
∴且O是AB的中点,
∴,
∵,
∴,
∴,
∴在中,,即半圆的半径为1。
(2)设CO=x,则在,因为,所以AC=2x,由勾股定理得: ,
即,解得(舍去)
∴,
∵半圆的半径为1,
∴半圆的面积为,
∴。
19.解:(1)∵OB=2,△AOB的面积为1,
∴B(﹣2,0),OA=1,
∴A(0,﹣1),
∴ , ∴,
∴y=﹣x﹣1;
又∵OD=4,OD⊥x轴,
∴C(﹣4,y),将x=﹣4代入y=﹣x﹣1,得y=1,
∴C(﹣4,1)
∴1=,
∴m=﹣4,
∴y=﹣;
(2)当x<0时,kx+b﹣>0的解集是x<﹣4.
20.(1)OA绕点O顺时针旋转120°至OB的位置.做BD垂直y轴
则OB与y轴夹角为30°
则在△OBD中 OB=4 BD=2 OD=2√3
则点B坐标为(-2,-2√3)
(2)抛物线方程y=ax +bx+c
已知点B(-2,-2√3) O(0,0) A(4,0)
代入方程解得
a=-√3/6
b=2√3/3
c=0
则抛物线方程y=(-√3/6)x +(2√3/3)x
(3)若△POB为等腰三角形
则过P做OB的中垂线PE垂足为E
OB的直线方程为y=√3x 则垂直于OB直线斜率为k=-1/√3
设直线PE为 y=kx+m
已知斜率为k=-1/√3,过E点(-1,-√3) 【OB中点】
解得m=-4√3/3
直线PE y=- √3x/3-4√3/3
联立直线、抛物线方程y=(-√3/6)x +(2√3/3)x
y=- √3x/3-4√3/3
的x -6x-8=0 二元一次方程根 x={-b±√(b2-4ac)}/2a
X1=3+√17 X2=3-√17
有根即存在点P
代入X1,X2
解得Y1=-(7√3/3+√51/3 ) Y2=-(7√3/3-√51/3 )
点P坐标P1(3+√17,-7√3/3-√51/3 ) P2(3-√17,-7√3/3+√51/3)
⌒
同课章节目录
