2025届高考物理二轮复习讲义:微专题1 传送带模型综合问题 (含解析)
文档属性
| 名称 | 2025届高考物理二轮复习讲义:微专题1 传送带模型综合问题 (含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 141.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-03 00:00:00 | ||
图片预览


文档简介
传送带模型综合问题可以分为动力学问题和能量问题
(1)传送带模型的动力学问题的难点在物体与传送带间的相对运动,物体运动状态发生变化的临界点是对地速度为零,物体与传送带间相对运动状态发生变化的临界点是相对速度为零,求解的关键点是摩擦力性质和方向的判断.
(2)传送带模型的能量问题主要涉及物体动能的变化和系统产生的热量.前者一般可用动能定理分析,要用到物体的对地位移,后者一般可用摩擦生热公式计算,要用到物体与皮带间的相对路程.
水平传送带综合问题
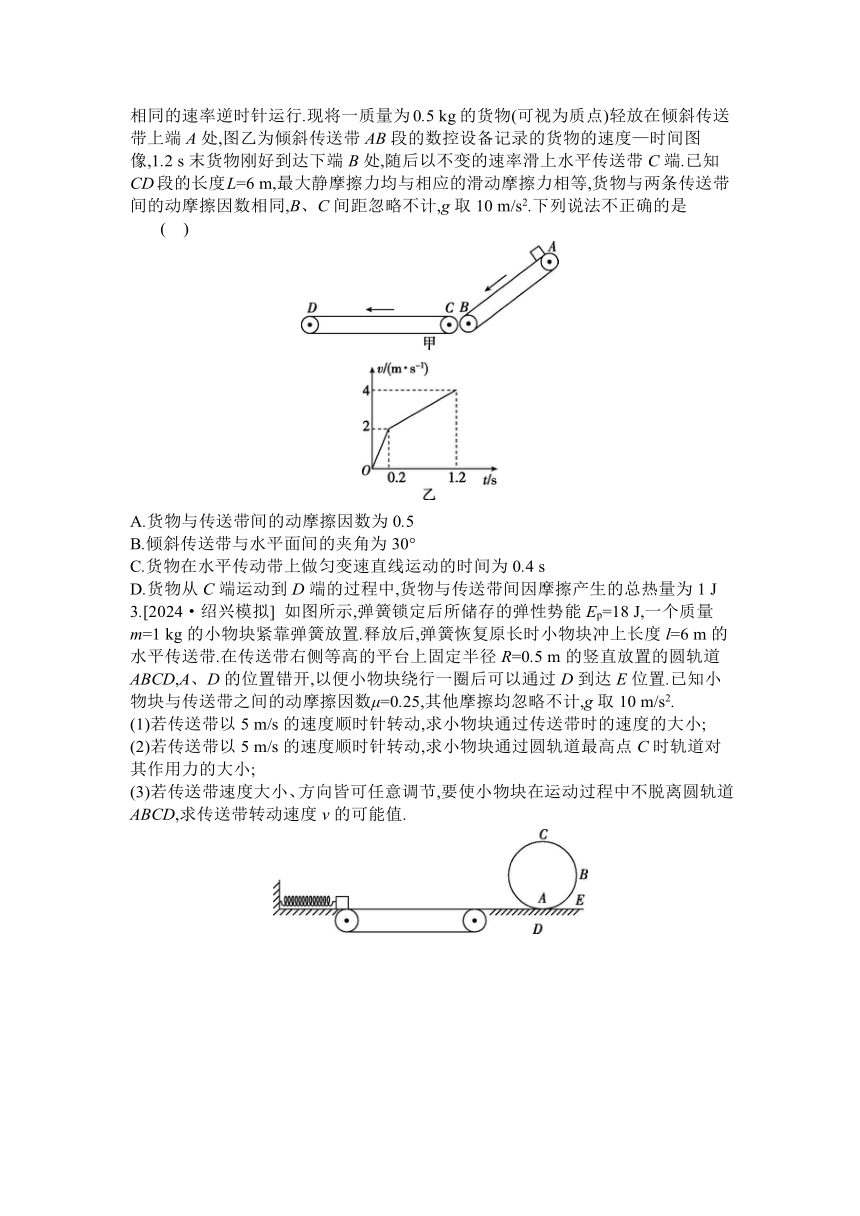
例1 [2024·绍兴模拟] 如图所示,绷紧的水平传送带始终以恒定速度4 m/s顺时针运行,质量为1 kg的小物块以6 m/s的初速度从传送带右端滑上传送带,经一段时间后小物块离开传送带.已知小物块与传送带间的动摩擦因数为0.2,传送带的长度为10 m,重力加速度g取10 m/s2.对上述过程,下列说法正确的是 ( )
A.小物块对传送带做功为20 J
B.小物块对传送带做功为48 J
C.带动传送带转动的电动机多做的功为40 J
D.带动传送带转动的电动机多做的功为50 J
【技法点拨】
1.小物块在传送带上做匀变速运动,一般仍选择地面为参考系进行求解,此时相关运动学公式、功的表达式中的位移、速度、加速度都是对地而言,不能用相对传送带的量代入计算.
2.小物块在传送带上先向左减速到零,再向右运动时,有两种可能性,当小物块的初速度大小比传送带速率小时,小物块向右一直做匀加速运动,当小物块的初速度大小比传送带速率大时,小物块向右先做匀加速运动,后相对传送带静止一起做匀速直线运动.
例2 某砂场为提高运输效率,研究砂粒下滑的高度与砂粒在传送带上运动的关系,建立如图所示的物理模型.竖直平面内有一倾角θ=37°的直轨道AB,其下方右侧放置一水平传送带,直轨道末端B与传送带间距可近似视为零,但允许小物块通过.转轮半径R=0.4 m、转轴间距L=2 m的传送带以恒定的线速度逆时针转动,转轮最低点离地面的高度H=2.2 m.现将一小物块放在距离传送带高h处由静止释放,小物块可从B与C之间通过,假设小物块从直轨道B端运动到达传送带上C点时,速度大小不变,方向变为水平向右.已知小物块与直轨道和传送带间的动摩擦因数均为μ=0.5.(sin 37°=0.6,cos 37°=0.8,g取10 m/s2)
(1)若h=2.4 m,求小物块到达B端时速度的大小;
(2)若小物块落到传送带左侧地面,求h需要满足的条件;
(3)改变小物块释放时距传递带的高度h,小物块从传送带的D点水平向右抛出,不计空气阻力,求小物块落地点到D点的水平距离x与h的关系式及h需要满足的条件.
倾斜传送带综合问题
例3 [2024·诸暨模拟] 如图甲所示为皮带输送机简化模型图,皮带输送机倾角θ=37°,顺时针匀速转动,在输送带下端A点无初速放入货物.货物可从下端A点运动到上端B点的过程中,其机械能E与位移x的关系图像(以A位置所在水平面为零势能面)如图乙所示.货物视为质点,质量m=10 kg,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8.下列说法正确的是 ( )
A.货物与输送带间的动摩擦因数为0.825
B.输送带A、B两端点间的距离为8 m
C.货物从下端A点运动到上端B点的时间为9 s
D.皮带输送机因运送该货物而多消耗的能量为585 J
【技法点拨】
1.物体沿倾斜传送带向下加速至与传送带共速后的运动有两种可能性,当满足μ≥tan θ时,物体与传送带相对静止一起做匀速直线运动,当满足μ2.电动机因传送物体而多消耗的电能有两种求法.方法一,用能量守恒定律求解,多消耗的电能等于物体机械能的变化和系统产生的热量之和.方法二,用功能关系求解,以传送带为研究对象,多消耗的电能等于传送者克服摩擦力做的功.
【跟踪训练】
1.(不定项)[2024·湖北黄石模拟] 如图所示,水平传送带以v=6 m/s的速度沿顺时针方向匀速转动,水平部分AB长为L,并与长为3.6 m的光滑倾斜轨道BC在B点平滑连接,BC与水平面的夹角为30°.现将一个可视为质点的工件从A点由静止释放,滑块与传送带间的动摩擦因数为μ,g取10 m/s2,要使工件能到达C点(没有施加其他外力辅助),下列关于μ和L的取值可能正确的是 ( )
A.μ=0.5,L=3 m B.μ=0.4,L=5 m
C.μ=0.3,L=6 m D.μ=0.2,L=7 m
2.中国国家邮政局监测数据显示,2023年1~4月中国快递业务量达300亿件,我们的生活离不开快递.图甲为快递物流配送分拣示意图,水平传送带和倾斜传送带以相同的速率逆时针运行.现将一质量为0.5 kg的货物(可视为质点)轻放在倾斜传送带上端A处,图乙为倾斜传送带AB段的数控设备记录的货物的速度—时间图像,1.2 s末货物刚好到达下端B处,随后以不变的速率滑上水平传送带C端.已知CD段的长度L=6 m,最大静摩擦力均与相应的滑动摩擦力相等,货物与两条传送带间的动摩擦因数相同,B、C间距忽略不计,g取10 m/s2.下列说法不正确的是 ( )
A.货物与传送带间的动摩擦因数为0.5
B.倾斜传送带与水平面间的夹角为30°
C.货物在水平传动带上做匀变速直线运动的时间为0.4 s
D.货物从C端运动到D端的过程中,货物与传送带间因摩擦产生的总热量为1 J
3.[2024·绍兴模拟] 如图所示,弹簧锁定后所储存的弹性势能Ep=18 J,一个质量m=1 kg的小物块紧靠弹簧放置.释放后,弹簧恢复原长时小物块冲上长度l=6 m的水平传送带.在传送带右侧等高的平台上固定半径R=0.5 m的竖直放置的圆轨道ABCD,A、D的位置错开,以便小物块绕行一圈后可以通过D到达E位置.已知小物块与传送带之间的动摩擦因数μ=0.25,其他摩擦均忽略不计,g取10 m/s2.
(1)若传送带以5 m/s的速度顺时针转动,求小物块通过传送带时的速度的大小;
(2)若传送带以5 m/s的速度顺时针转动,求小物块通过圆轨道最高点C时轨道对其作用力的大小;
(3)若传送带速度大小、方向皆可任意调节,要使小物块在运动过程中不脱离圆轨道ABCD,求传送带转动速度v的可能值.
参考答案与详细解析
例1 C [解析] 小物块的加速度大小为a==2 m/s2,小物块向左减速至0过程的位移为x==9 m,小物块向左运动的时间为t1==3 s,由于x<10 m,所以之后小物块向右运动至与传送带共速,所用的时间为t2==2 s,小物块对传送带做功为W=-μmgv(t1+t2)=-40 J,A、B错误;全程小物块与传送带的相对位移为Δx=+vt1+vt2-a=25 m,根据功能关系可知,带动传送带转动的电动机多做的功为W'=μmgΔx-m-mv2=40 J,C正确,D错误.
例2 (1)4 m/s (2)h<3.0 m
(3)x=2,h≥3.6 m
[解析] (1)物块由静止释放到B的过程中,有mgsin θ-μmgcos θ=ma
=2a
联立解得vB=4 m/s
(2)要使物块由传送带左侧离开,应使物块到达D点之前速度减小为零,由动能定理有
mgh-μmgcos θ-μmgL<0
解得h<3.0 m
(3)物块从传送带右侧抛出,设到达D点的速度为v,有
mgh-μmgcos θ-μmgL=mv2
H+2R=gt2
x=vt
联立可得x=2
为使物块能在D点水平抛出,应有
mg≤
解得h≥3.6 m
例3 C [解析] 由题图可知,货物从开始运动到与传送带相对静止,货物的位移x货=0.5 m,货物增加的机械能ΔE1=35 J,由功能关系得ΔE1=μmgcos 37°·x货,解得货物与输送带间的动摩擦因数μ=0.875,故A错误;由图像可知,物块沿传送带向上运动0.5 m后与传送带相对静止,此后物块的动能不变,重力势能增加,摩擦力变为静摩擦力,货物运动到B点时又增加的机械能ΔE2=(515-35) J=480 J,由功能关系得mgx2sin 37°=ΔE2,解得x2=8 m,则传送带A、B两端点之间的距离为L=x货+x2=8.5 m,故B错误;设加速阶段的加速度大小为a,加速阶段时间为t1,有μmgcos 37°-mgsin 37°=ma,x货=a,v2=2ax货,解得t1=1 s,v=1 m/s,设匀速阶段时间为t2,有x2=vt2,解得t=8 s,所以货物从下端A点运动到上端B点的时间为t=t1+t2=9 s,故C正确;由能量守恒定律可知,皮带输送机因运送该货物而多消耗的能量为E=μmgcos 37°·Δx1+mv2+mgLsin 37°,其中Δx1=x传-x货=vt1-a=0.5 m,解得E=550 J,故D错误.
【跟踪训练】
1.BC [解析] 设工件运动到B点的速度为vB时能恰好到达C点,根据机械能守恒定律得m=mgxBCsin 30°,解得vB=6 m/s,此速度恰好与传送带速度相等,说明工件在水平传送带上运动到B点前已与传送带共速,根据动能定理得μmgx=m,且x≤L,解得μL≥1.8 m,代入选项数据可知,B、C正确,A、D错误.
2.B [解析] 由图像可知,0~0.2 s内,货物在倾斜传送带上的加速度大小为a1== m/s2=10 m/s2,0.2~1.2 s内,货物在倾斜传送带上的加速度大小为a2== m/s2=2 m/s2,根据牛顿第二定律,0~0.2 s内,有mgsin θ+μmgcos θ=ma1,0.2~1.2 s内,有mgsin θ-μmgcos θ=ma2,联立解得sin θ=0.6,μ=0.5,故A正确,B错误;由图像可知,传送带的速率v=2 m/s,货物在水平传送带上运动的加速度大小为a=,货物在水平传送带上做匀变速运动到与传送带共速需要的时间t3=,货物的位移大小为x=t3,联立解得t3=0.4 s,x=1.2 m,由于x3.(1)5 m/s (2)0 (3)传送带顺时针转动,v≥5 m/s或0≤v≤ m/s;或者传送带逆时针转动,速度取任意值
[解析] (1)设小物块释放后,冲上水平传送带时的速度大小为v0,根据题意,由能量守恒定律可得Ep=m
解得v0=6 m/s
小物块冲上传送带后做匀减速运动,设其加速度大小为a,根据牛顿第二定律有μmg=ma
解得a=2.5 m/s2
设小物块与传送带共速时对地位移为x,传送带速度为v1,则由运动学公式可得-=2ax
解得x=2.2 m
由于x(2)设小物块通过圆轨道最高点时的速度为v2,轨道对小物块的弹力为FN,则小物块滑出传送带后运动到圆轨道最高点C过程,由动能定理有-2mgR=m-m
在最高点C时,由牛顿第二定律可得FN+mg=m
联立解得FN=0
(3)要使小物块在运动过程中不脱离圆轨道ABCD,有两种可能情况:
情况一:小物块能运动到圆轨道的最高点C.
当小物块恰好能运动到圆轨道的最高点时,小物块对轨道的压力为零,由第(2)问可知,此时传送带顺时针转动且速度为5 m/s,所以当传送带顺时针转动且速度v≥5 m/s时,小物块能运动到圆轨道最高点而不脱离圆轨道.
情况二:小物块沿圆轨道运动的最高点不高于圆轨道的圆心.
小物块从离开传送带至运动到最高处,由机械能守恒定律得
m=mgh
其中h≤R
解得小物块离开传送带的速度v3≤ m/s
现在确定小物块离开传动带的最小速度:若小物块在传送带上一直做匀减速运动到离开传动带,则小物块离开传送带的速度最小,由运动学公式得-=-2gl
解得小物块离开传动带的最小速度v4= m/s
由于v4≤v3,说明情况二存在.
对于情况二,小物块的运动情况有两种类型:一是小物块一直匀减速通过传送带,此种情况下小物块以 m/s的速度运动到圆轨道底端;二是小物块在传送带上先匀减速运动,速度减小到与传送带速度相等后,小物块与传送带一起相对静止运动直至离开传送带,此种情况下小物块以大于 m/s而小于等于 m/s的速度运动到圆轨道的底端.传送带的速度分成两种类型:一是传动带逆时针转动,速度可以是任意值;二是传送带顺时针转动,且速度v≤ m/s.
综上所述,要使小物块在运动过程中不脱离圆轨道ABCD,传动带的速度v的可能取值是:传动带顺时针转动,v≥5 m/s或0≤v≤ m/s;或者传送带逆时针转动,速度取任意值.
(1)传送带模型的动力学问题的难点在物体与传送带间的相对运动,物体运动状态发生变化的临界点是对地速度为零,物体与传送带间相对运动状态发生变化的临界点是相对速度为零,求解的关键点是摩擦力性质和方向的判断.
(2)传送带模型的能量问题主要涉及物体动能的变化和系统产生的热量.前者一般可用动能定理分析,要用到物体的对地位移,后者一般可用摩擦生热公式计算,要用到物体与皮带间的相对路程.
水平传送带综合问题
例1 [2024·绍兴模拟] 如图所示,绷紧的水平传送带始终以恒定速度4 m/s顺时针运行,质量为1 kg的小物块以6 m/s的初速度从传送带右端滑上传送带,经一段时间后小物块离开传送带.已知小物块与传送带间的动摩擦因数为0.2,传送带的长度为10 m,重力加速度g取10 m/s2.对上述过程,下列说法正确的是 ( )
A.小物块对传送带做功为20 J
B.小物块对传送带做功为48 J
C.带动传送带转动的电动机多做的功为40 J
D.带动传送带转动的电动机多做的功为50 J
【技法点拨】
1.小物块在传送带上做匀变速运动,一般仍选择地面为参考系进行求解,此时相关运动学公式、功的表达式中的位移、速度、加速度都是对地而言,不能用相对传送带的量代入计算.
2.小物块在传送带上先向左减速到零,再向右运动时,有两种可能性,当小物块的初速度大小比传送带速率小时,小物块向右一直做匀加速运动,当小物块的初速度大小比传送带速率大时,小物块向右先做匀加速运动,后相对传送带静止一起做匀速直线运动.
例2 某砂场为提高运输效率,研究砂粒下滑的高度与砂粒在传送带上运动的关系,建立如图所示的物理模型.竖直平面内有一倾角θ=37°的直轨道AB,其下方右侧放置一水平传送带,直轨道末端B与传送带间距可近似视为零,但允许小物块通过.转轮半径R=0.4 m、转轴间距L=2 m的传送带以恒定的线速度逆时针转动,转轮最低点离地面的高度H=2.2 m.现将一小物块放在距离传送带高h处由静止释放,小物块可从B与C之间通过,假设小物块从直轨道B端运动到达传送带上C点时,速度大小不变,方向变为水平向右.已知小物块与直轨道和传送带间的动摩擦因数均为μ=0.5.(sin 37°=0.6,cos 37°=0.8,g取10 m/s2)
(1)若h=2.4 m,求小物块到达B端时速度的大小;
(2)若小物块落到传送带左侧地面,求h需要满足的条件;
(3)改变小物块释放时距传递带的高度h,小物块从传送带的D点水平向右抛出,不计空气阻力,求小物块落地点到D点的水平距离x与h的关系式及h需要满足的条件.
倾斜传送带综合问题
例3 [2024·诸暨模拟] 如图甲所示为皮带输送机简化模型图,皮带输送机倾角θ=37°,顺时针匀速转动,在输送带下端A点无初速放入货物.货物可从下端A点运动到上端B点的过程中,其机械能E与位移x的关系图像(以A位置所在水平面为零势能面)如图乙所示.货物视为质点,质量m=10 kg,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8.下列说法正确的是 ( )
A.货物与输送带间的动摩擦因数为0.825
B.输送带A、B两端点间的距离为8 m
C.货物从下端A点运动到上端B点的时间为9 s
D.皮带输送机因运送该货物而多消耗的能量为585 J
【技法点拨】
1.物体沿倾斜传送带向下加速至与传送带共速后的运动有两种可能性,当满足μ≥tan θ时,物体与传送带相对静止一起做匀速直线运动,当满足μ
【跟踪训练】
1.(不定项)[2024·湖北黄石模拟] 如图所示,水平传送带以v=6 m/s的速度沿顺时针方向匀速转动,水平部分AB长为L,并与长为3.6 m的光滑倾斜轨道BC在B点平滑连接,BC与水平面的夹角为30°.现将一个可视为质点的工件从A点由静止释放,滑块与传送带间的动摩擦因数为μ,g取10 m/s2,要使工件能到达C点(没有施加其他外力辅助),下列关于μ和L的取值可能正确的是 ( )
A.μ=0.5,L=3 m B.μ=0.4,L=5 m
C.μ=0.3,L=6 m D.μ=0.2,L=7 m
2.中国国家邮政局监测数据显示,2023年1~4月中国快递业务量达300亿件,我们的生活离不开快递.图甲为快递物流配送分拣示意图,水平传送带和倾斜传送带以相同的速率逆时针运行.现将一质量为0.5 kg的货物(可视为质点)轻放在倾斜传送带上端A处,图乙为倾斜传送带AB段的数控设备记录的货物的速度—时间图像,1.2 s末货物刚好到达下端B处,随后以不变的速率滑上水平传送带C端.已知CD段的长度L=6 m,最大静摩擦力均与相应的滑动摩擦力相等,货物与两条传送带间的动摩擦因数相同,B、C间距忽略不计,g取10 m/s2.下列说法不正确的是 ( )
A.货物与传送带间的动摩擦因数为0.5
B.倾斜传送带与水平面间的夹角为30°
C.货物在水平传动带上做匀变速直线运动的时间为0.4 s
D.货物从C端运动到D端的过程中,货物与传送带间因摩擦产生的总热量为1 J
3.[2024·绍兴模拟] 如图所示,弹簧锁定后所储存的弹性势能Ep=18 J,一个质量m=1 kg的小物块紧靠弹簧放置.释放后,弹簧恢复原长时小物块冲上长度l=6 m的水平传送带.在传送带右侧等高的平台上固定半径R=0.5 m的竖直放置的圆轨道ABCD,A、D的位置错开,以便小物块绕行一圈后可以通过D到达E位置.已知小物块与传送带之间的动摩擦因数μ=0.25,其他摩擦均忽略不计,g取10 m/s2.
(1)若传送带以5 m/s的速度顺时针转动,求小物块通过传送带时的速度的大小;
(2)若传送带以5 m/s的速度顺时针转动,求小物块通过圆轨道最高点C时轨道对其作用力的大小;
(3)若传送带速度大小、方向皆可任意调节,要使小物块在运动过程中不脱离圆轨道ABCD,求传送带转动速度v的可能值.
参考答案与详细解析
例1 C [解析] 小物块的加速度大小为a==2 m/s2,小物块向左减速至0过程的位移为x==9 m,小物块向左运动的时间为t1==3 s,由于x<10 m,所以之后小物块向右运动至与传送带共速,所用的时间为t2==2 s,小物块对传送带做功为W=-μmgv(t1+t2)=-40 J,A、B错误;全程小物块与传送带的相对位移为Δx=+vt1+vt2-a=25 m,根据功能关系可知,带动传送带转动的电动机多做的功为W'=μmgΔx-m-mv2=40 J,C正确,D错误.
例2 (1)4 m/s (2)h<3.0 m
(3)x=2,h≥3.6 m
[解析] (1)物块由静止释放到B的过程中,有mgsin θ-μmgcos θ=ma
=2a
联立解得vB=4 m/s
(2)要使物块由传送带左侧离开,应使物块到达D点之前速度减小为零,由动能定理有
mgh-μmgcos θ-μmgL<0
解得h<3.0 m
(3)物块从传送带右侧抛出,设到达D点的速度为v,有
mgh-μmgcos θ-μmgL=mv2
H+2R=gt2
x=vt
联立可得x=2
为使物块能在D点水平抛出,应有
mg≤
解得h≥3.6 m
例3 C [解析] 由题图可知,货物从开始运动到与传送带相对静止,货物的位移x货=0.5 m,货物增加的机械能ΔE1=35 J,由功能关系得ΔE1=μmgcos 37°·x货,解得货物与输送带间的动摩擦因数μ=0.875,故A错误;由图像可知,物块沿传送带向上运动0.5 m后与传送带相对静止,此后物块的动能不变,重力势能增加,摩擦力变为静摩擦力,货物运动到B点时又增加的机械能ΔE2=(515-35) J=480 J,由功能关系得mgx2sin 37°=ΔE2,解得x2=8 m,则传送带A、B两端点之间的距离为L=x货+x2=8.5 m,故B错误;设加速阶段的加速度大小为a,加速阶段时间为t1,有μmgcos 37°-mgsin 37°=ma,x货=a,v2=2ax货,解得t1=1 s,v=1 m/s,设匀速阶段时间为t2,有x2=vt2,解得t=8 s,所以货物从下端A点运动到上端B点的时间为t=t1+t2=9 s,故C正确;由能量守恒定律可知,皮带输送机因运送该货物而多消耗的能量为E=μmgcos 37°·Δx1+mv2+mgLsin 37°,其中Δx1=x传-x货=vt1-a=0.5 m,解得E=550 J,故D错误.
【跟踪训练】
1.BC [解析] 设工件运动到B点的速度为vB时能恰好到达C点,根据机械能守恒定律得m=mgxBCsin 30°,解得vB=6 m/s,此速度恰好与传送带速度相等,说明工件在水平传送带上运动到B点前已与传送带共速,根据动能定理得μmgx=m,且x≤L,解得μL≥1.8 m,代入选项数据可知,B、C正确,A、D错误.
2.B [解析] 由图像可知,0~0.2 s内,货物在倾斜传送带上的加速度大小为a1== m/s2=10 m/s2,0.2~1.2 s内,货物在倾斜传送带上的加速度大小为a2== m/s2=2 m/s2,根据牛顿第二定律,0~0.2 s内,有mgsin θ+μmgcos θ=ma1,0.2~1.2 s内,有mgsin θ-μmgcos θ=ma2,联立解得sin θ=0.6,μ=0.5,故A正确,B错误;由图像可知,传送带的速率v=2 m/s,货物在水平传送带上运动的加速度大小为a=,货物在水平传送带上做匀变速运动到与传送带共速需要的时间t3=,货物的位移大小为x=t3,联立解得t3=0.4 s,x=1.2 m,由于x
[解析] (1)设小物块释放后,冲上水平传送带时的速度大小为v0,根据题意,由能量守恒定律可得Ep=m
解得v0=6 m/s
小物块冲上传送带后做匀减速运动,设其加速度大小为a,根据牛顿第二定律有μmg=ma
解得a=2.5 m/s2
设小物块与传送带共速时对地位移为x,传送带速度为v1,则由运动学公式可得-=2ax
解得x=2.2 m
由于x
在最高点C时,由牛顿第二定律可得FN+mg=m
联立解得FN=0
(3)要使小物块在运动过程中不脱离圆轨道ABCD,有两种可能情况:
情况一:小物块能运动到圆轨道的最高点C.
当小物块恰好能运动到圆轨道的最高点时,小物块对轨道的压力为零,由第(2)问可知,此时传送带顺时针转动且速度为5 m/s,所以当传送带顺时针转动且速度v≥5 m/s时,小物块能运动到圆轨道最高点而不脱离圆轨道.
情况二:小物块沿圆轨道运动的最高点不高于圆轨道的圆心.
小物块从离开传送带至运动到最高处,由机械能守恒定律得
m=mgh
其中h≤R
解得小物块离开传送带的速度v3≤ m/s
现在确定小物块离开传动带的最小速度:若小物块在传送带上一直做匀减速运动到离开传动带,则小物块离开传送带的速度最小,由运动学公式得-=-2gl
解得小物块离开传动带的最小速度v4= m/s
由于v4≤v3,说明情况二存在.
对于情况二,小物块的运动情况有两种类型:一是小物块一直匀减速通过传送带,此种情况下小物块以 m/s的速度运动到圆轨道底端;二是小物块在传送带上先匀减速运动,速度减小到与传送带速度相等后,小物块与传送带一起相对静止运动直至离开传送带,此种情况下小物块以大于 m/s而小于等于 m/s的速度运动到圆轨道的底端.传送带的速度分成两种类型:一是传动带逆时针转动,速度可以是任意值;二是传送带顺时针转动,且速度v≤ m/s.
综上所述,要使小物块在运动过程中不脱离圆轨道ABCD,传动带的速度v的可能取值是:传动带顺时针转动,v≥5 m/s或0≤v≤ m/s;或者传送带逆时针转动,速度取任意值.
同课章节目录
