人教版数学(2024)七年级下册第一次月考训练试题(基础)(含答案)
文档属性
| 名称 | 人教版数学(2024)七年级下册第一次月考训练试题(基础)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 326.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-03 15:43:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学(2024)七年级下册第一次月考训练试题(基础)
一、填空题
1.a,b,c为同一平面内三条不同的直线,若a⊥b,c⊥b,则a与c的位置关系是 .
2.一把直尺和一个含角的直角三角板按如图方式叠合在一起(三角板的直角顶点在直尺的边上),若,则的度数是 .
3.填空并完成以下证明:已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
证明:FH⊥AB(已知)
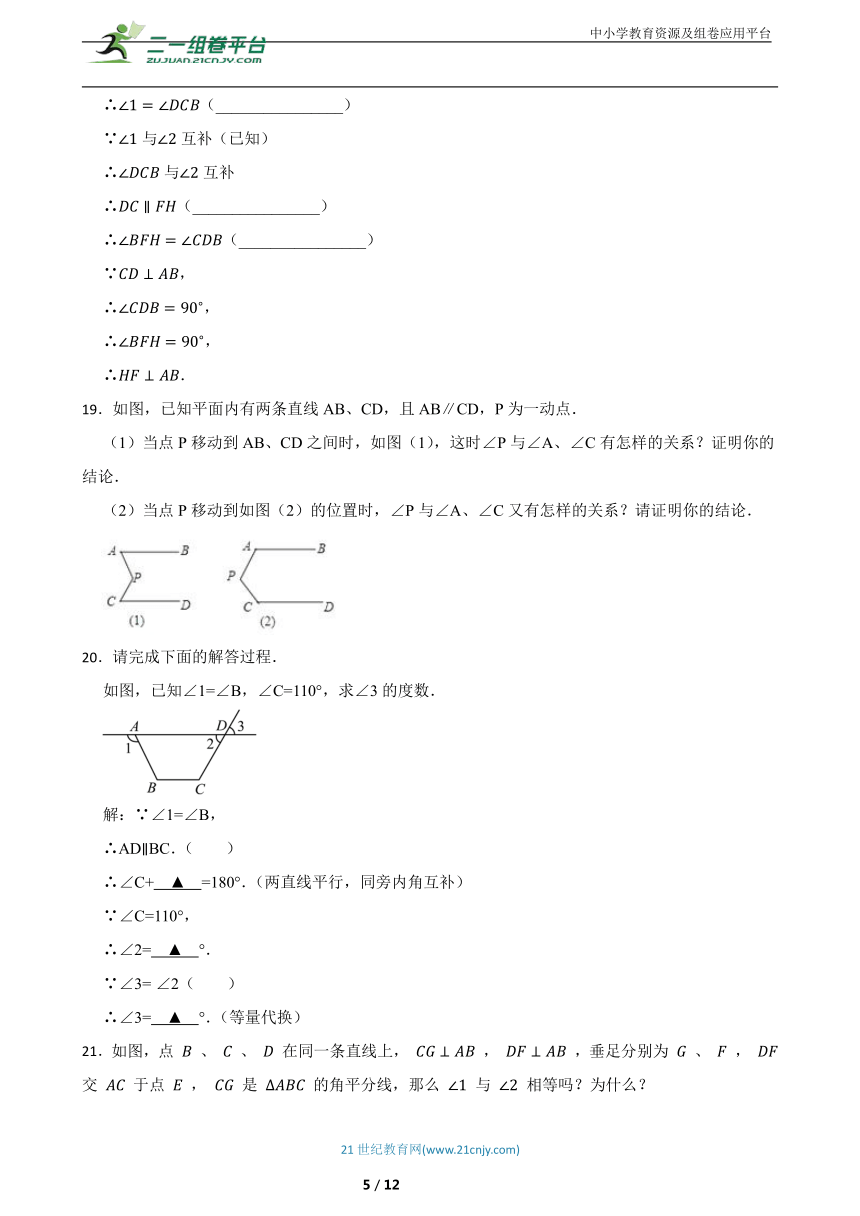
∴∠BHF= .
∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2=∠BCD.( )
∵∠2=∠3(已知)
∴∠3= .(等量代换)
∴CD∥ .(内错角相等,两直线平行)
∴∠BDC=∠BHF=90°(两直线平行,同位角相等)
∴CD⊥AB.
4.如图,AB∥CD,∠B=34°,∠D=41°,则∠BED的度数为 .
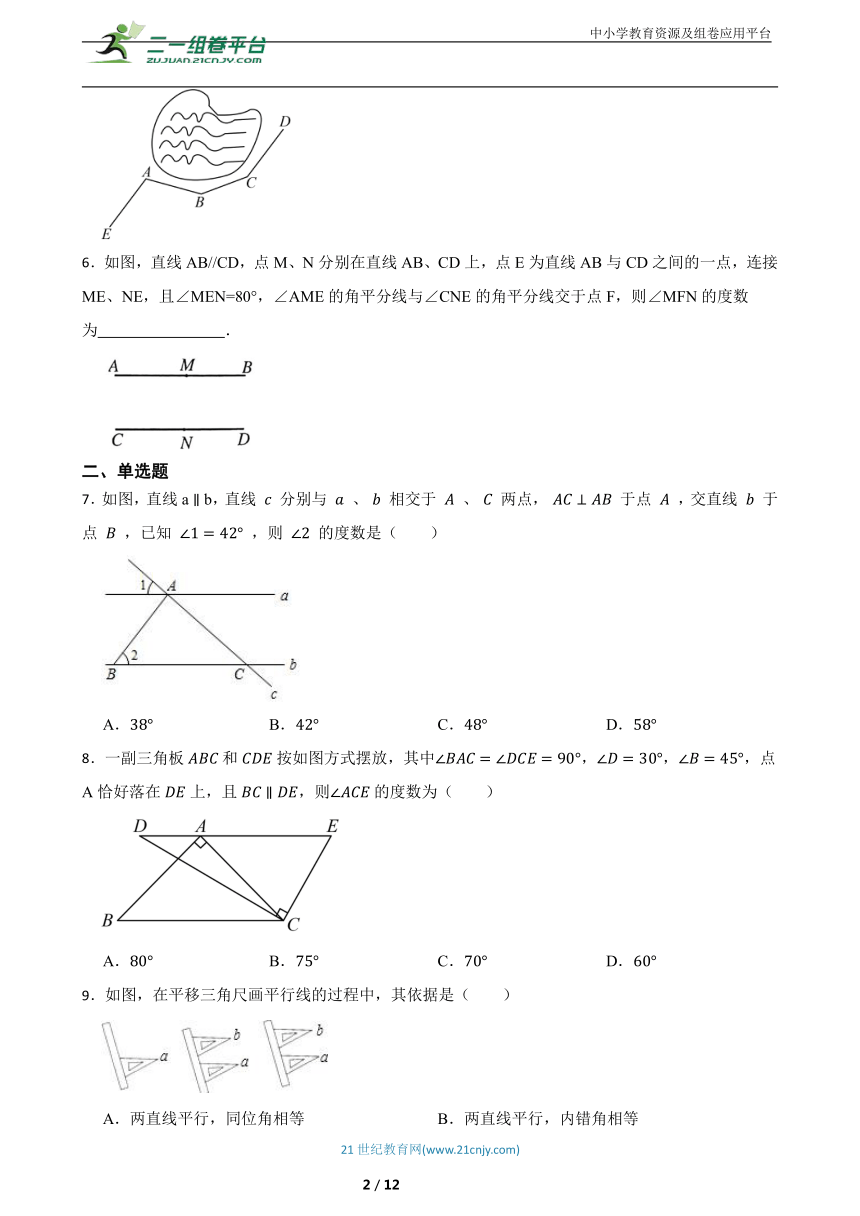
5.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是
6.如图,直线AB//CD,点M、N分别在直线AB、CD上,点E为直线AB与CD之间的一点,连接ME、NE,且∠MEN=80°,∠AME的角平分线与∠CNE的角平分线交于点F,则∠MFN的度数为 .
二、单选题
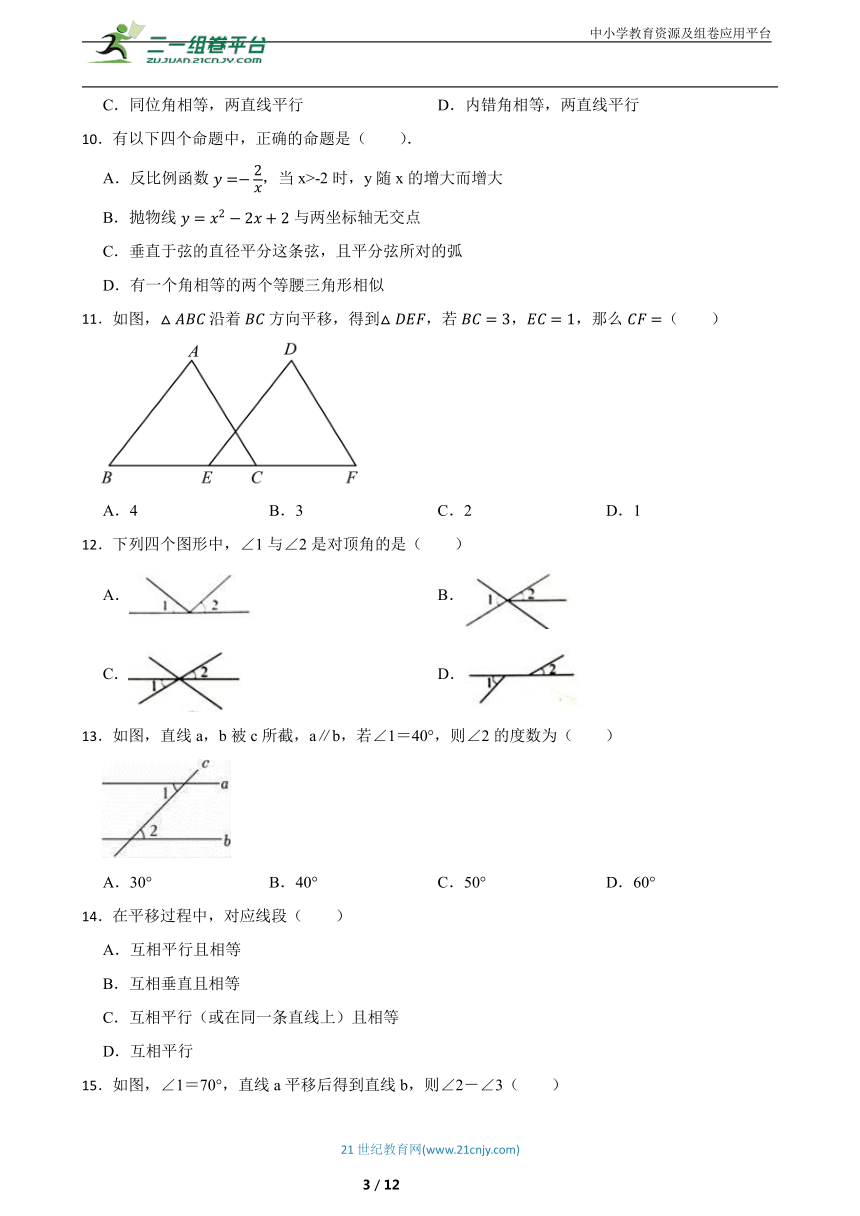
7.如图,直线a b,直线 分别与 、 相交于 、 两点, 于点 ,交直线 于点 ,已知 ,则 的度数是( )
A. B. C. D.
8.一副三角板和按如图方式摆放,其中,,,点A恰好落在上,且,则的度数为( )
A. B. C. D.
9.如图,在平移三角尺画平行线的过程中,其依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
10.有以下四个命题中,正确的命题是( ).
A.反比例函数,当x>-2时,y随x的增大而增大
B.抛物线与两坐标轴无交点
C.垂直于弦的直径平分这条弦,且平分弦所对的弧
D.有一个角相等的两个等腰三角形相似
11.如图,沿着方向平移,得到,若,,那么( )
A.4 B.3 C.2 D.1
12.下列四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
13.如图,直线a,b被c所截,a∥b,若∠1=40°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
14.在平移过程中,对应线段( )
A.互相平行且相等
B.互相垂直且相等
C.互相平行(或在同一条直线上)且相等
D.互相平行
15.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3( )
A.70° B.180° C.110° D.80°
16.如图,AB∥CD,将一副直角三角尺按如图摆放,∠GEF=60°,∠MNP=45°。有下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN。其中正确的个数是( )
A.1 B.2 C.3 D.4
三、解答题
17.如图,直线a//b,直线与,分别相交于,两点,交于点,∠1=40°,求∠2的度数.
18.如图,已知,与互补,判断与是否垂直,并说明理由.
解:垂直,理由如下:
∵
∴(垂直定义)
∴(_________________)
∴(________________)
∵与互补(已知)
∴与互补
∴(________________)
∴(________________)
∵,
∴,
∴,
∴.
19.如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论.
(2)当点P移动到如图(2)的位置时,∠P与∠A、∠C又有怎样的关系?请证明你的结论.
20.请完成下面的解答过程.
如图,已知∠1=∠B,∠C=110°,求∠3的度数.
解:∵∠1=∠B,
∴ADBC.( )
∴∠C+ ▲ =180°.(两直线平行,同旁内角互补)
∵∠C=110°,
∴∠2= ▲ °.
∵∠3= ∠2( )
∴∠3= ▲ °.(等量代换)
21.如图,点 、 、 在同一条直线上, , ,垂足分别为 、 , 交 于点 , 是 的角平分线,那么 与 相等吗?为什么?
22.如图,直线AB相与CD相交于O,OF,OD分别是,平分线.
(1)写出∠DOE的两个补角:
(2)若.求∠BOC和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
四、计算题
23.如图,,,, ,求:的度数.
请完成下面的推理和计算过程,并在括号内写明依据.
∵(已知)
∴ ① ( ② )
∵(已知)
∴ ③
∵(已知)
∴
∴ ④
∴ ⑤
∴( ⑥ )
∴ ⑦
∵
∴ ⑧° .
24.如图, , , ,求 、 的度数.
25.如图,直线分别交直线于点G,H,射线分别在和的内部,且.
(1)若和互补.
①求的度数;
②当,且时,求的度数;
(2)设,.若,求m,n满足的等量关系.
答案解析部分
1.【答案】a∥c
【知识点】平行公理及推论
2.【答案】
【知识点】角的运算;平行线的性质
3.【答案】90°;同位角相等,两直线平行;两直线平行,内错角相等;∠BCD;FH
【知识点】平行线的判定与性质
4.【答案】75°
【知识点】平行线的性质
5.【答案】150°
【知识点】平行线的判定与性质
6.【答案】40°或140°
【知识点】角的运算;平行线的性质;角平分线的概念
7.【答案】C
【知识点】角的运算;平行线的性质
8.【答案】B
【知识点】平行线的性质
9.【答案】C
【知识点】平行线的判定
10.【答案】C
【知识点】真命题与假命题
11.【答案】C
【知识点】平移的性质
12.【答案】C
【知识点】对顶角及其性质
13.【答案】B
【知识点】平行线的性质
14.【答案】A
【知识点】平移的性质
15.【答案】C
【知识点】平行线的判定与性质
16.【答案】D
【知识点】平行线的判定;平行线的性质
17.【答案】∠2=50°
【知识点】余角、补角及其性质;平行线的性质
18.【答案】同位角相等,两直线平行;两直线平行,内错角相等;同旁内角互补,两直线平行;两直线平行,同位角相等;
【知识点】平行线的判定与性质
19.【答案】证明:(1)∠P=∠A+∠C,
如图(1)延长AP交CD与点E.
∵AB∥CD,
∴∠A=∠AEC.
又∵∠APC是△PCE的外角,
∴∠APC=∠C+∠AEC.
∴∠APC=∠A+∠C;
(2)∠P=360°﹣(∠A+∠C).
如图(2)延长BA到E,延长DC到F,
由(1)得∠P=∠PAE+∠PCF.
∵∠PAE=180°﹣∠PAB,∠PCF=180°﹣∠PCD,
∴∠P=360°﹣(∠PAB+∠PCD).
【知识点】平行线的性质
20.【答案】解:∵∠1=∠B,
∴AD BC.(内错角相等,两直线平行),
∴∠C+∠2=180°.(两直线平行,同旁内角互补)
∵∠C=110°,
∴∠2=70°,
∵∠3=∠2.(对顶角相等)
∴∠3=70°(等量代换)
【知识点】平行线的性质
21.【答案】解: (或直接写相等).
因为 , ,
所以 ,
所以 ∥ ,
所以 , ,
因为 是 的角平分线,
所以
所以
【知识点】垂线的概念;平行线的判定与性质;角平分线的概念
22.【答案】(1)解:∠DOE 的补角为:∠COE,∠AOD,∠BOC.
(2)解:∵OD是∠BOE 的平分线,
∴∠DOE=∠BOD=30°,∠BOE=60°;
∵∠BOC=180°﹣∠BOD,
∴∠BOC=150°;
∵∠AOE=180°﹣∠BOE,
∴∠AOE=120°;
又∵OF是∠AOE 的平分线,
∴∠EOF=∠AOE=60°
(3)解:射线OD与OF互相垂直.理由如下:
∵OF,OD分别是∠AOE,∠BOE的平分线,
∴∠DOF=∠DOE+∠EOF=∠BOE+∠EOA=(∠BOE+∠EOA)=×180°=90°.
∴OD⊥OF.
即射线OD、OF的位置关系是垂直.
【知识点】角的运算;余角、补角及其性质;对顶角及其性质;角平分线的概念
23.【答案】① ②两直线平行,同位角相等 ③ ④ ⑤ ⑥内错角相等,两直线平行 ⑦ ⑧115°.
【知识点】平行线的判定与性质
24.【答案】解: ,
.
,
,
.
的度数为 , 的度数为 .
【知识点】平行线的性质
25.【答案】(1)解:①和互补,
.
,
,
;
②由①得,
,
,
又,
,
.
,
,
;
(2)解:,
.
设,
,,
,
,
又,
,
,
,
即m,n满足的等量关系为.
【知识点】角的运算;平行线的性质;邻补角
21世纪教育网(www.21cnjy.com)
2 / 12
人教版数学(2024)七年级下册第一次月考训练试题(基础)
一、填空题
1.a,b,c为同一平面内三条不同的直线,若a⊥b,c⊥b,则a与c的位置关系是 .
2.一把直尺和一个含角的直角三角板按如图方式叠合在一起(三角板的直角顶点在直尺的边上),若,则的度数是 .
3.填空并完成以下证明:已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
证明:FH⊥AB(已知)
∴∠BHF= .
∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2=∠BCD.( )
∵∠2=∠3(已知)
∴∠3= .(等量代换)
∴CD∥ .(内错角相等,两直线平行)
∴∠BDC=∠BHF=90°(两直线平行,同位角相等)
∴CD⊥AB.
4.如图,AB∥CD,∠B=34°,∠D=41°,则∠BED的度数为 .
5.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是
6.如图,直线AB//CD,点M、N分别在直线AB、CD上,点E为直线AB与CD之间的一点,连接ME、NE,且∠MEN=80°,∠AME的角平分线与∠CNE的角平分线交于点F,则∠MFN的度数为 .
二、单选题
7.如图,直线a b,直线 分别与 、 相交于 、 两点, 于点 ,交直线 于点 ,已知 ,则 的度数是( )
A. B. C. D.
8.一副三角板和按如图方式摆放,其中,,,点A恰好落在上,且,则的度数为( )
A. B. C. D.
9.如图,在平移三角尺画平行线的过程中,其依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
10.有以下四个命题中,正确的命题是( ).
A.反比例函数,当x>-2时,y随x的增大而增大
B.抛物线与两坐标轴无交点
C.垂直于弦的直径平分这条弦,且平分弦所对的弧
D.有一个角相等的两个等腰三角形相似
11.如图,沿着方向平移,得到,若,,那么( )
A.4 B.3 C.2 D.1
12.下列四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
13.如图,直线a,b被c所截,a∥b,若∠1=40°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
14.在平移过程中,对应线段( )
A.互相平行且相等
B.互相垂直且相等
C.互相平行(或在同一条直线上)且相等
D.互相平行
15.如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3( )
A.70° B.180° C.110° D.80°
16.如图,AB∥CD,将一副直角三角尺按如图摆放,∠GEF=60°,∠MNP=45°。有下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN。其中正确的个数是( )
A.1 B.2 C.3 D.4
三、解答题
17.如图,直线a//b,直线与,分别相交于,两点,交于点,∠1=40°,求∠2的度数.
18.如图,已知,与互补,判断与是否垂直,并说明理由.
解:垂直,理由如下:
∵
∴(垂直定义)
∴(_________________)
∴(________________)
∵与互补(已知)
∴与互补
∴(________________)
∴(________________)
∵,
∴,
∴,
∴.
19.如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论.
(2)当点P移动到如图(2)的位置时,∠P与∠A、∠C又有怎样的关系?请证明你的结论.
20.请完成下面的解答过程.
如图,已知∠1=∠B,∠C=110°,求∠3的度数.
解:∵∠1=∠B,
∴ADBC.( )
∴∠C+ ▲ =180°.(两直线平行,同旁内角互补)
∵∠C=110°,
∴∠2= ▲ °.
∵∠3= ∠2( )
∴∠3= ▲ °.(等量代换)
21.如图,点 、 、 在同一条直线上, , ,垂足分别为 、 , 交 于点 , 是 的角平分线,那么 与 相等吗?为什么?
22.如图,直线AB相与CD相交于O,OF,OD分别是,平分线.
(1)写出∠DOE的两个补角:
(2)若.求∠BOC和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
四、计算题
23.如图,,,, ,求:的度数.
请完成下面的推理和计算过程,并在括号内写明依据.
∵(已知)
∴ ① ( ② )
∵(已知)
∴ ③
∵(已知)
∴
∴ ④
∴ ⑤
∴( ⑥ )
∴ ⑦
∵
∴ ⑧° .
24.如图, , , ,求 、 的度数.
25.如图,直线分别交直线于点G,H,射线分别在和的内部,且.
(1)若和互补.
①求的度数;
②当,且时,求的度数;
(2)设,.若,求m,n满足的等量关系.
答案解析部分
1.【答案】a∥c
【知识点】平行公理及推论
2.【答案】
【知识点】角的运算;平行线的性质
3.【答案】90°;同位角相等,两直线平行;两直线平行,内错角相等;∠BCD;FH
【知识点】平行线的判定与性质
4.【答案】75°
【知识点】平行线的性质
5.【答案】150°
【知识点】平行线的判定与性质
6.【答案】40°或140°
【知识点】角的运算;平行线的性质;角平分线的概念
7.【答案】C
【知识点】角的运算;平行线的性质
8.【答案】B
【知识点】平行线的性质
9.【答案】C
【知识点】平行线的判定
10.【答案】C
【知识点】真命题与假命题
11.【答案】C
【知识点】平移的性质
12.【答案】C
【知识点】对顶角及其性质
13.【答案】B
【知识点】平行线的性质
14.【答案】A
【知识点】平移的性质
15.【答案】C
【知识点】平行线的判定与性质
16.【答案】D
【知识点】平行线的判定;平行线的性质
17.【答案】∠2=50°
【知识点】余角、补角及其性质;平行线的性质
18.【答案】同位角相等,两直线平行;两直线平行,内错角相等;同旁内角互补,两直线平行;两直线平行,同位角相等;
【知识点】平行线的判定与性质
19.【答案】证明:(1)∠P=∠A+∠C,
如图(1)延长AP交CD与点E.
∵AB∥CD,
∴∠A=∠AEC.
又∵∠APC是△PCE的外角,
∴∠APC=∠C+∠AEC.
∴∠APC=∠A+∠C;
(2)∠P=360°﹣(∠A+∠C).
如图(2)延长BA到E,延长DC到F,
由(1)得∠P=∠PAE+∠PCF.
∵∠PAE=180°﹣∠PAB,∠PCF=180°﹣∠PCD,
∴∠P=360°﹣(∠PAB+∠PCD).
【知识点】平行线的性质
20.【答案】解:∵∠1=∠B,
∴AD BC.(内错角相等,两直线平行),
∴∠C+∠2=180°.(两直线平行,同旁内角互补)
∵∠C=110°,
∴∠2=70°,
∵∠3=∠2.(对顶角相等)
∴∠3=70°(等量代换)
【知识点】平行线的性质
21.【答案】解: (或直接写相等).
因为 , ,
所以 ,
所以 ∥ ,
所以 , ,
因为 是 的角平分线,
所以
所以
【知识点】垂线的概念;平行线的判定与性质;角平分线的概念
22.【答案】(1)解:∠DOE 的补角为:∠COE,∠AOD,∠BOC.
(2)解:∵OD是∠BOE 的平分线,
∴∠DOE=∠BOD=30°,∠BOE=60°;
∵∠BOC=180°﹣∠BOD,
∴∠BOC=150°;
∵∠AOE=180°﹣∠BOE,
∴∠AOE=120°;
又∵OF是∠AOE 的平分线,
∴∠EOF=∠AOE=60°
(3)解:射线OD与OF互相垂直.理由如下:
∵OF,OD分别是∠AOE,∠BOE的平分线,
∴∠DOF=∠DOE+∠EOF=∠BOE+∠EOA=(∠BOE+∠EOA)=×180°=90°.
∴OD⊥OF.
即射线OD、OF的位置关系是垂直.
【知识点】角的运算;余角、补角及其性质;对顶角及其性质;角平分线的概念
23.【答案】① ②两直线平行,同位角相等 ③ ④ ⑤ ⑥内错角相等,两直线平行 ⑦ ⑧115°.
【知识点】平行线的判定与性质
24.【答案】解: ,
.
,
,
.
的度数为 , 的度数为 .
【知识点】平行线的性质
25.【答案】(1)解:①和互补,
.
,
,
;
②由①得,
,
,
又,
,
.
,
,
;
(2)解:,
.
设,
,,
,
,
又,
,
,
,
即m,n满足的等量关系为.
【知识点】角的运算;平行线的性质;邻补角
21世纪教育网(www.21cnjy.com)
2 / 12
同课章节目录
