人教版数学(2024)七年级下册第一次月考训练试题(精华)(含答案)
文档属性
| 名称 | 人教版数学(2024)七年级下册第一次月考训练试题(精华)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 743.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 14:47:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学(2024)七年级下册第一次月考训练试题(精华)
一、填空题
1.(2023九上·杭州开学考)若平行四边形中两个内角的度数比为:,则其中较大角的度数是 .
2.(2024七下·西岗期末)如图,将一副三角板中含角的三角板放置在平面上不动,另一个含角的三角板绕着它们相同的直角顶点О旋转一周,在旋转过程中,当与平行时,的度数是 .
3.(2023七下·高陵期末)如图,直线分别与直线相交于点平分,交直线于点,若,则的度数为 .
4.(2023八上·天津市月考)如图,,,请你添加一个条件: ,使.(写出一个条件即可)
5.(2024九上·上海市期中)如图,在中,是上一点,,点E是上一动点,连接 ,并作,射线交线段于点F,连接.如果与相似,那么 .
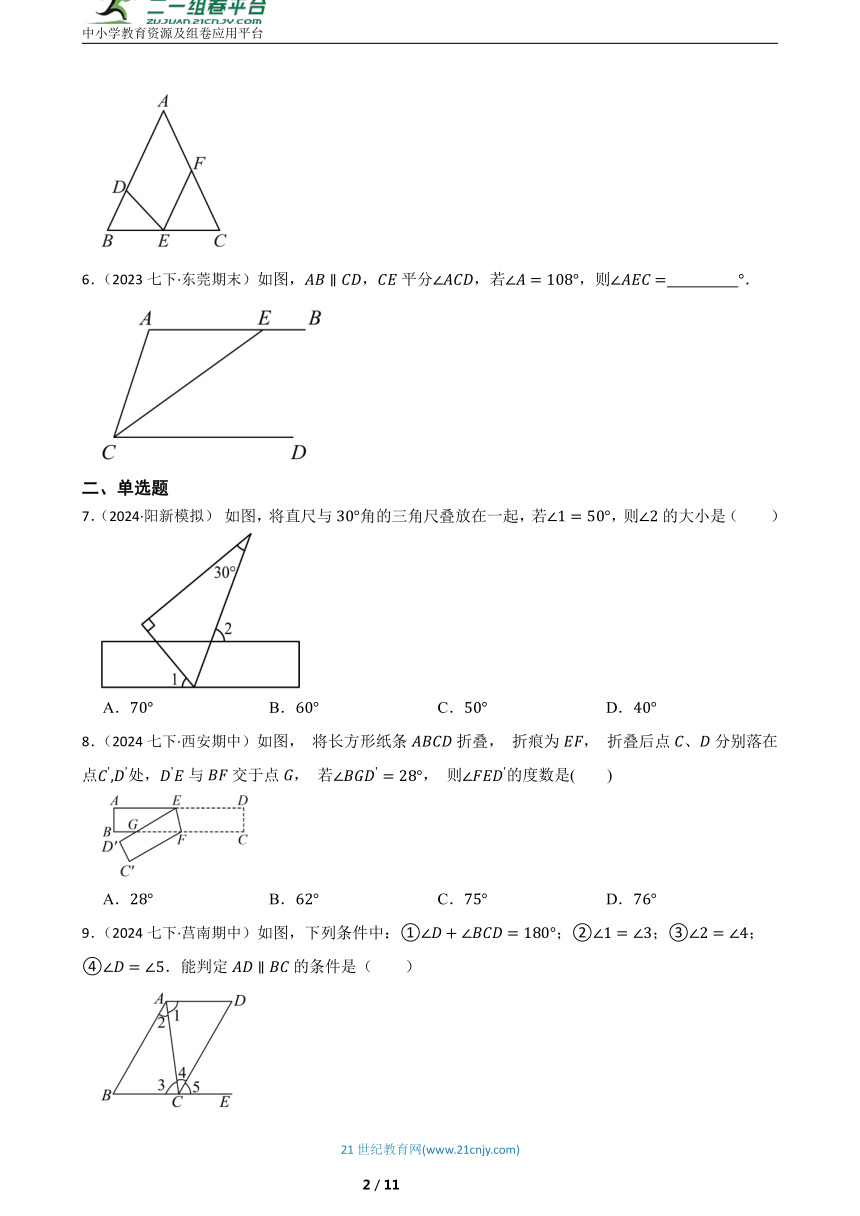
6.(2023七下·东莞期末)如图,,平分,若,则 .
二、单选题
7.(2024·阳新模拟) 如图,将直尺与角的三角尺叠放在一起,若,则的大小是( )
A. B. C. D.
8.(2024七下·西安期中)如图, 将长方形纸条折叠, 折痕为, 折叠后点、分别落在点处,与交于点, 若, 则的度数是( )
A. B. C. D.
9.(2024七下·莒南期中)如图,下列条件中:①;②;③;④.能判定的条件是( )
A.①②③④ B.①②③ C.①②④ D.①③④
10.(2024八下·中原月考)下列命题的逆命题是真命题的个数是( )
①有两边相等的三角形是等腰三角形;②到角的两边的距离相等的点在这个角的平分线上;③直角三角形的两个锐角互余;④全等三角形的面积相等
A.1个 B.2个 C.3个 D.4个
11.(2024八上·海淀月考)在图中,,,.有下列结论:
①沿直线翻折,可得到;
②把沿线段的垂直平分线翻折,可得到;
③把沿射线方向平移与相等的长度,可得到.
其中所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
12.(2024七下·郑州经济技术开发月考)下列说法正确的是( )
A.平面内,过一点有且只有一条直线与已知直线垂直;
B.有公共顶点且相等的角是对顶角;
C.直线外一点到已知直线的垂线段,叫做这点到直线的距离;
D.过一点有且只有一条直线与已知直线平行.
13.(2024九上·玄武期中)如图,在中,,是弦,点D在的延长线上,连接,,若,,则的度数是( )
A. B. C. D.
14.(2024九下·灞桥模拟)如图,平面直角坐标系中,已知点,使点B平移至原点O,得到,则的长为( )
A. B. C. D.1
15.(2024七下·榆树期中)把一副三角板按如图所示平放在桌面上,点E恰好落在的延长线上,,则的大小为( )
A. B. C. D.
16.(2024·杭州模拟)如图,在△ABC中,点D是AB上一点(不与点A,B重合),过点D作DE∥BC交AC于点E,过点E作EF//AB交BC于点F,点G是线段DE上一点,EG=2DG,点H是线段CF上一点,CH=2HF,连接AG,AH,GH,HE. 若已知△AGH的面积,则一定能求出( )
A.△ABC的面积 B.△ADE的面积
C.四边形DBFE的面积 D.△EFC的面积
三、解答题
17.(2024七下·桦甸期末)如图,直线a//b,直线与,分别相交于,两点,交于点,∠1=40°,求∠2的度数.
18.(2024七下·滕州期中)推理填空:
如图,,,,求的度数.
解:因为,
所以_____(______)
又因为,
所以,(______)
所以____(______)
所以_____ ,(______)
又因为,
所以_____ .
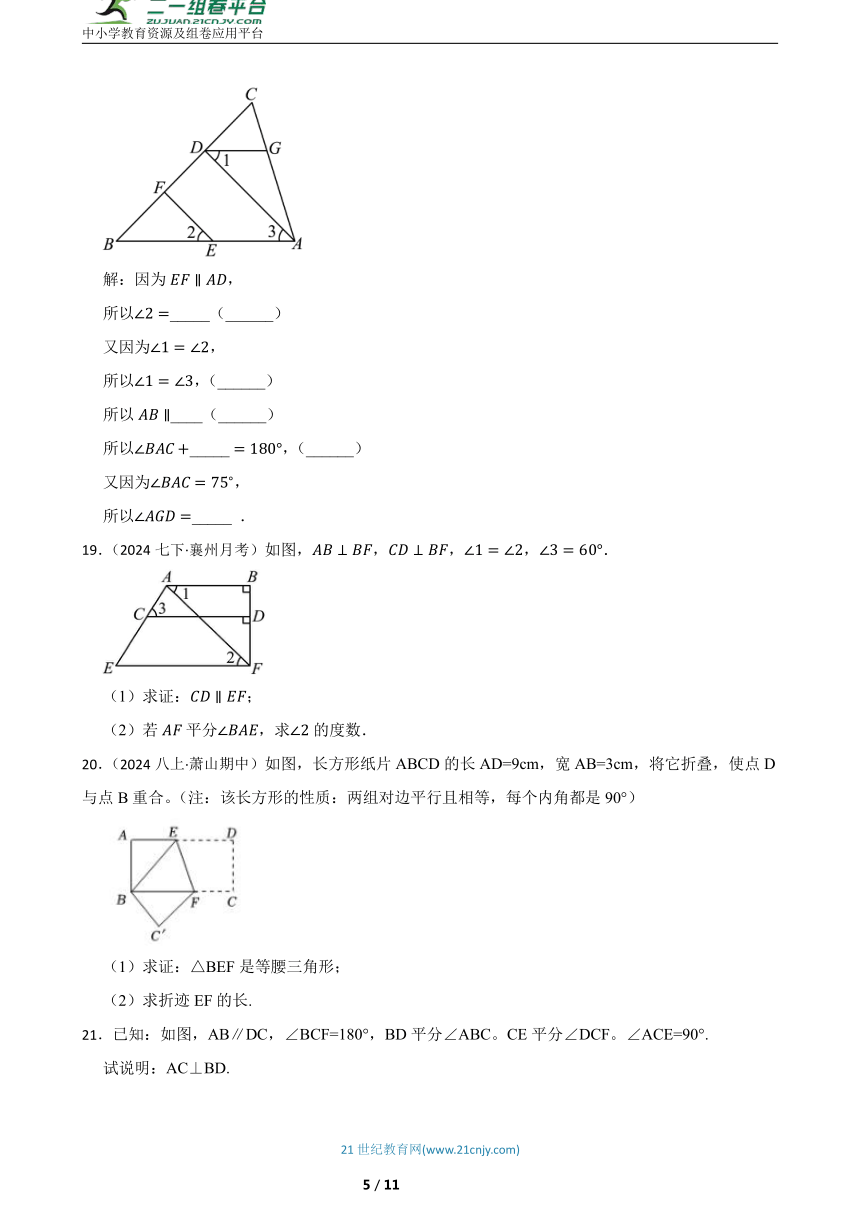
19.(2024七下·襄州月考)如图,,,,.
(1)求证:;
(2)若平分,求的度数.
20.(2024八上·萧山期中)如图,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合。(注:该长方形的性质:两组对边平行且相等,每个内角都是90°)
(1)求证:△BEF是等腰三角形;
(2)求折迹EF的长.
21.已知:如图,AB∥DC,∠BCF=180°,BD平分∠ABC。CE平分∠DCF。∠ACE=90°.
试说明:AC⊥BD.
22.如图,点O在直线AC上,∠AOB=55°.用量角器作出∠BOC的角平分线OD,并计算∠AOD的度数.
四、计算题
23.(2023七下·赣县区期末)计算:
(1)计算:;
(2)如图,直线、,已知,,求的度数.
24.(2023九上·鹿城月考)如图,一吸管杯放置在水平桌面上,矩形为其横截面,为吸管,,当杯子绕点按顺时针方向转动到与水平线平行时(如图).
(1)的度数为______.
(2)请根据自身能力从以下两小题中选一题完成,
求图中点到水平线的距离.
由图到图,点的位置是升高了还是下降了?变化了多少厘米?(结果精确到,参考数据:)
25.(2024九下·光明模拟)地球有多大?多年前,古希腊数学家埃拉托斯特尼()利用太阳光线测量出了地球子午线的周长.下面让我们一起开启“探求地球周长”的数学项目化学习之旅.
项目任务 (一) 如图1,某日正午,小红在B地(与太阳直射点A在同一子午线上)测得太阳光与木棍的夹角为,则______,若测得之间弧长为l,则地球子午线周长为______.(用含,l的代数式表示)
项目任务 (二) 如图2,某日正午,小红和小明在同一子午线的B地、C地测得太阳光与木棍的夹角分别为,,则______,若测得之间弧长为l,则地球子午线周长为______.(用含,,l的代数式表示)
项目任务 (三) 如图3,日落时,身高为h的小亮趴在地上平视远方,在太阳完全从地平线上消失的一瞬间,按下秒表开始计时.同时马上站起来,当太阳再次完全消失在地平线的瞬间,停止计时,小亮利用这个时间差和地球自转的速度计算出了,请据此计算出地球的半径与周长.(用含h,的代数式表示)
答案解析部分
1.【答案】
【知识点】平行公理及推论
2.【答案】或
【知识点】角的运算;平行线的性质;三角形的外角性质;邻补角
3.【答案】151°
【知识点】平行线的判定与性质;角平分线的概念
4.【答案】(答案不唯一)
【知识点】平行线的性质;三角形全等及其性质;三角形全等的判定-ASA
5.【答案】2或
【知识点】平行线的判定与性质;三角形的角平分线、中线和高;等腰三角形的判定与性质;相似三角形的性质
6.【答案】36
【知识点】角的运算;平行线的性质;角平分线的概念
7.【答案】A
【知识点】角的运算;平行线的性质;含30°角的直角三角形
8.【答案】D
【知识点】平行线的性质;翻折变换(折叠问题)
9.【答案】C
【知识点】平行线的判定
10.【答案】C
【知识点】角平分线的性质;直角三角形的性质;真命题与假命题;逆命题
11.【答案】A
【知识点】三角形全等及其性质;翻折变换(折叠问题);平移的性质
12.【答案】A
【知识点】垂线的概念;点到直线的距离;平行公理及推论;对顶角及其性质
13.【答案】D
【知识点】平行线的性质;三角形内角和定理;等腰三角形的性质;圆与三角形的综合
14.【答案】A
【知识点】坐标与图形性质;平移的性质;相似三角形的判定与性质
15.【答案】A
【知识点】角的运算;平行线的性质;平行线的判定与性质
16.【答案】B
【知识点】平行线的判定;平行线的性质;三角形的面积;相似三角形的性质;相似三角形的判定
17.【答案】∠2=50°
【知识点】余角、补角及其性质;平行线的性质
18.【答案】,两直线平行,同位角相等;等量代换;,内错角相等,两直线平行;,两直线平行,同旁内角互补;
【知识点】平行线的判定与性质
19.【答案】(1)证明:∵,,
∴,
∴,
∵,
∴,
∴
(2)解:∵,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴.
【知识点】垂线的概念;平行公理及推论;平行线的判定;平行线的性质;角平分线的概念
20.【答案】(1)证明:∵四边形ABCD是长方形,
∴BC∥AD,
∴∠DEF=∠EFB,
由折叠得∠DEF=∠BEF,
∴∠BEF=∠BFE,
∴BE=BF,
∴△BEF是等腰三角形;
(2)解:过点E作EH⊥BC于点H,则∠BHE=∠FHE=90°,
由折叠得BE=DE,
设BE=DE=xcm,则AE=(9-x)cm,
在Rt△ABE中,∠A=90°,AB=3cm,
由勾股定理得AB2+AE2=BE2,即32+(9-x)2=x2,
解得x=5,即BF=BE=5,
∴AE=9-5=4cm,
∵AD∥BC,AB∥EH,
∴AB=EH=3,BH=AE=4,
∴FH=BF-BH=1,
在Rt△EFH中,cm,即折痕EF长为cm.
【知识点】平行线的性质;等腰三角形的判定;勾股定理;翻折变换(折叠问题)
21.【答案】解:∵AB∥CD,∴∠ABC=∠DCF.∵BD平分∠ABC,CE 平分∠DCF,
∴∠DBC=∠ECF.∴BD∥CE.∴∠AGD=∠ACE.∵∠ACE=90°,∴∠AGD=90°,即AC⊥BD.
【知识点】垂线的概念;平行线的判定与性质;角平分线的概念
22.【答案】解:如图:
∵∠AOB=55°,
∴∠BOC=180°-55°=125°,
∵OD平分∠BOC,
∴,
∴∠AOD=∠AOB+∠BOD=55°+62.5°=117.5°.
【知识点】角的运算;余角、补角及其性质;角平分线的概念
23.【答案】(1)
(2)
【知识点】平行线的判定与性质;求算术平方根;开立方(求立方根)
24.【答案】(1);
(2)点到水平线的距离为;点的位置是下降了,降低了.
【知识点】平行线的性质;解直角三角形
25.【答案】任务(一):,;任务(二):,;任务(三):地球的半径为,地球的周长
【知识点】平行线的性质;切线的性质;弧长的计算;解直角三角形的其他实际应用
21世纪教育网(www.21cnjy.com)
2 / 11
人教版数学(2024)七年级下册第一次月考训练试题(精华)
一、填空题
1.(2023九上·杭州开学考)若平行四边形中两个内角的度数比为:,则其中较大角的度数是 .
2.(2024七下·西岗期末)如图,将一副三角板中含角的三角板放置在平面上不动,另一个含角的三角板绕着它们相同的直角顶点О旋转一周,在旋转过程中,当与平行时,的度数是 .
3.(2023七下·高陵期末)如图,直线分别与直线相交于点平分,交直线于点,若,则的度数为 .
4.(2023八上·天津市月考)如图,,,请你添加一个条件: ,使.(写出一个条件即可)
5.(2024九上·上海市期中)如图,在中,是上一点,,点E是上一动点,连接 ,并作,射线交线段于点F,连接.如果与相似,那么 .
6.(2023七下·东莞期末)如图,,平分,若,则 .
二、单选题
7.(2024·阳新模拟) 如图,将直尺与角的三角尺叠放在一起,若,则的大小是( )
A. B. C. D.
8.(2024七下·西安期中)如图, 将长方形纸条折叠, 折痕为, 折叠后点、分别落在点处,与交于点, 若, 则的度数是( )
A. B. C. D.
9.(2024七下·莒南期中)如图,下列条件中:①;②;③;④.能判定的条件是( )
A.①②③④ B.①②③ C.①②④ D.①③④
10.(2024八下·中原月考)下列命题的逆命题是真命题的个数是( )
①有两边相等的三角形是等腰三角形;②到角的两边的距离相等的点在这个角的平分线上;③直角三角形的两个锐角互余;④全等三角形的面积相等
A.1个 B.2个 C.3个 D.4个
11.(2024八上·海淀月考)在图中,,,.有下列结论:
①沿直线翻折,可得到;
②把沿线段的垂直平分线翻折,可得到;
③把沿射线方向平移与相等的长度,可得到.
其中所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
12.(2024七下·郑州经济技术开发月考)下列说法正确的是( )
A.平面内,过一点有且只有一条直线与已知直线垂直;
B.有公共顶点且相等的角是对顶角;
C.直线外一点到已知直线的垂线段,叫做这点到直线的距离;
D.过一点有且只有一条直线与已知直线平行.
13.(2024九上·玄武期中)如图,在中,,是弦,点D在的延长线上,连接,,若,,则的度数是( )
A. B. C. D.
14.(2024九下·灞桥模拟)如图,平面直角坐标系中,已知点,使点B平移至原点O,得到,则的长为( )
A. B. C. D.1
15.(2024七下·榆树期中)把一副三角板按如图所示平放在桌面上,点E恰好落在的延长线上,,则的大小为( )
A. B. C. D.
16.(2024·杭州模拟)如图,在△ABC中,点D是AB上一点(不与点A,B重合),过点D作DE∥BC交AC于点E,过点E作EF//AB交BC于点F,点G是线段DE上一点,EG=2DG,点H是线段CF上一点,CH=2HF,连接AG,AH,GH,HE. 若已知△AGH的面积,则一定能求出( )
A.△ABC的面积 B.△ADE的面积
C.四边形DBFE的面积 D.△EFC的面积
三、解答题
17.(2024七下·桦甸期末)如图,直线a//b,直线与,分别相交于,两点,交于点,∠1=40°,求∠2的度数.
18.(2024七下·滕州期中)推理填空:
如图,,,,求的度数.
解:因为,
所以_____(______)
又因为,
所以,(______)
所以____(______)
所以_____ ,(______)
又因为,
所以_____ .
19.(2024七下·襄州月考)如图,,,,.
(1)求证:;
(2)若平分,求的度数.
20.(2024八上·萧山期中)如图,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合。(注:该长方形的性质:两组对边平行且相等,每个内角都是90°)
(1)求证:△BEF是等腰三角形;
(2)求折迹EF的长.
21.已知:如图,AB∥DC,∠BCF=180°,BD平分∠ABC。CE平分∠DCF。∠ACE=90°.
试说明:AC⊥BD.
22.如图,点O在直线AC上,∠AOB=55°.用量角器作出∠BOC的角平分线OD,并计算∠AOD的度数.
四、计算题
23.(2023七下·赣县区期末)计算:
(1)计算:;
(2)如图,直线、,已知,,求的度数.
24.(2023九上·鹿城月考)如图,一吸管杯放置在水平桌面上,矩形为其横截面,为吸管,,当杯子绕点按顺时针方向转动到与水平线平行时(如图).
(1)的度数为______.
(2)请根据自身能力从以下两小题中选一题完成,
求图中点到水平线的距离.
由图到图,点的位置是升高了还是下降了?变化了多少厘米?(结果精确到,参考数据:)
25.(2024九下·光明模拟)地球有多大?多年前,古希腊数学家埃拉托斯特尼()利用太阳光线测量出了地球子午线的周长.下面让我们一起开启“探求地球周长”的数学项目化学习之旅.
项目任务 (一) 如图1,某日正午,小红在B地(与太阳直射点A在同一子午线上)测得太阳光与木棍的夹角为,则______,若测得之间弧长为l,则地球子午线周长为______.(用含,l的代数式表示)
项目任务 (二) 如图2,某日正午,小红和小明在同一子午线的B地、C地测得太阳光与木棍的夹角分别为,,则______,若测得之间弧长为l,则地球子午线周长为______.(用含,,l的代数式表示)
项目任务 (三) 如图3,日落时,身高为h的小亮趴在地上平视远方,在太阳完全从地平线上消失的一瞬间,按下秒表开始计时.同时马上站起来,当太阳再次完全消失在地平线的瞬间,停止计时,小亮利用这个时间差和地球自转的速度计算出了,请据此计算出地球的半径与周长.(用含h,的代数式表示)
答案解析部分
1.【答案】
【知识点】平行公理及推论
2.【答案】或
【知识点】角的运算;平行线的性质;三角形的外角性质;邻补角
3.【答案】151°
【知识点】平行线的判定与性质;角平分线的概念
4.【答案】(答案不唯一)
【知识点】平行线的性质;三角形全等及其性质;三角形全等的判定-ASA
5.【答案】2或
【知识点】平行线的判定与性质;三角形的角平分线、中线和高;等腰三角形的判定与性质;相似三角形的性质
6.【答案】36
【知识点】角的运算;平行线的性质;角平分线的概念
7.【答案】A
【知识点】角的运算;平行线的性质;含30°角的直角三角形
8.【答案】D
【知识点】平行线的性质;翻折变换(折叠问题)
9.【答案】C
【知识点】平行线的判定
10.【答案】C
【知识点】角平分线的性质;直角三角形的性质;真命题与假命题;逆命题
11.【答案】A
【知识点】三角形全等及其性质;翻折变换(折叠问题);平移的性质
12.【答案】A
【知识点】垂线的概念;点到直线的距离;平行公理及推论;对顶角及其性质
13.【答案】D
【知识点】平行线的性质;三角形内角和定理;等腰三角形的性质;圆与三角形的综合
14.【答案】A
【知识点】坐标与图形性质;平移的性质;相似三角形的判定与性质
15.【答案】A
【知识点】角的运算;平行线的性质;平行线的判定与性质
16.【答案】B
【知识点】平行线的判定;平行线的性质;三角形的面积;相似三角形的性质;相似三角形的判定
17.【答案】∠2=50°
【知识点】余角、补角及其性质;平行线的性质
18.【答案】,两直线平行,同位角相等;等量代换;,内错角相等,两直线平行;,两直线平行,同旁内角互补;
【知识点】平行线的判定与性质
19.【答案】(1)证明:∵,,
∴,
∴,
∵,
∴,
∴
(2)解:∵,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴.
【知识点】垂线的概念;平行公理及推论;平行线的判定;平行线的性质;角平分线的概念
20.【答案】(1)证明:∵四边形ABCD是长方形,
∴BC∥AD,
∴∠DEF=∠EFB,
由折叠得∠DEF=∠BEF,
∴∠BEF=∠BFE,
∴BE=BF,
∴△BEF是等腰三角形;
(2)解:过点E作EH⊥BC于点H,则∠BHE=∠FHE=90°,
由折叠得BE=DE,
设BE=DE=xcm,则AE=(9-x)cm,
在Rt△ABE中,∠A=90°,AB=3cm,
由勾股定理得AB2+AE2=BE2,即32+(9-x)2=x2,
解得x=5,即BF=BE=5,
∴AE=9-5=4cm,
∵AD∥BC,AB∥EH,
∴AB=EH=3,BH=AE=4,
∴FH=BF-BH=1,
在Rt△EFH中,cm,即折痕EF长为cm.
【知识点】平行线的性质;等腰三角形的判定;勾股定理;翻折变换(折叠问题)
21.【答案】解:∵AB∥CD,∴∠ABC=∠DCF.∵BD平分∠ABC,CE 平分∠DCF,
∴∠DBC=∠ECF.∴BD∥CE.∴∠AGD=∠ACE.∵∠ACE=90°,∴∠AGD=90°,即AC⊥BD.
【知识点】垂线的概念;平行线的判定与性质;角平分线的概念
22.【答案】解:如图:
∵∠AOB=55°,
∴∠BOC=180°-55°=125°,
∵OD平分∠BOC,
∴,
∴∠AOD=∠AOB+∠BOD=55°+62.5°=117.5°.
【知识点】角的运算;余角、补角及其性质;角平分线的概念
23.【答案】(1)
(2)
【知识点】平行线的判定与性质;求算术平方根;开立方(求立方根)
24.【答案】(1);
(2)点到水平线的距离为;点的位置是下降了,降低了.
【知识点】平行线的性质;解直角三角形
25.【答案】任务(一):,;任务(二):,;任务(三):地球的半径为,地球的周长
【知识点】平行线的性质;切线的性质;弧长的计算;解直角三角形的其他实际应用
21世纪教育网(www.21cnjy.com)
2 / 11
同课章节目录
