人教版数学(2024)七年级下册期中训练卷(含答案)
文档属性
| 名称 | 人教版数学(2024)七年级下册期中训练卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 427.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 14:55:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学(2024)七年级下册期中训练卷
一、单选题
1.“辉煌九秩,筑梦百年”,在巴蜀中学建校90周年之际,八年级学生王小明制作了一批手工艺品送给母校作纪念,每一件工艺品都包含一个礼盒和三张礼卡,已知材料可制作10个礼盒或50张礼卡,现有材料,并且制作出来的礼卡和礼盒刚好全部配套.设用材料用来制作礼盒,材料用来制作礼卡.则可列方程组( )
A. B.
C. D.
2.若是关于x、y的方程的一组解,则m的值为( )
A.—2 B.2 C.—4 D.4
3.如图,, , 若,那么的度数是( )
A. B. C. D.
4.在平面直角坐标系中到y轴的距离是( )
A.3 B.4 C.5 D.
5.点位于( )
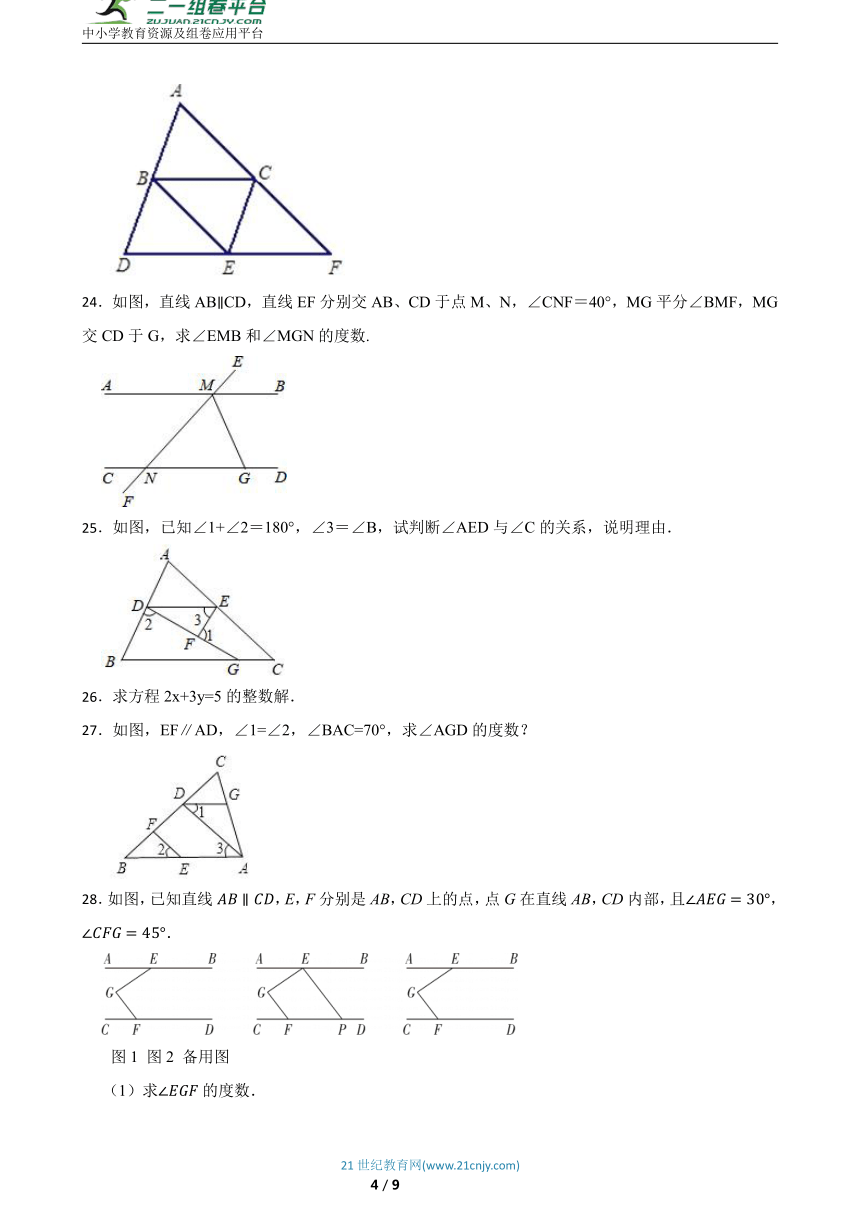
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.把无理数表示在数轴上,在这四个数中,被墨迹(如图所示)覆盖住的无理数是( )
A.8 B. C. D.
7.如图,将四边形先向右平移4个单位,再向上平移2个单位,那么点的对应点的坐标是( )
A. B. C. D.
8.若是关于、的方程的一个解,则的值是( )
A.5 B. C.8 D.
9.在实数四个数中,最小的是( )
A. B.-3.14 C. D.0
10.如图,AB∥CD,∠ABK的平分线BE的反向延长线和∠DCK的平分线CF的反向延长线相交于点H,∠K-∠H=27°,则∠K=( )
A.82° B.80° C.78° D.76°
二、填空题
11.在平面直角坐标系中,有点 ,点 ,当线段 轴,且 时,则 .
12.点A的坐标(4,-3),它到x轴的距离为
13.如图,在四边形中,,相交于点O,则与面积相等的三角形是 .
14.若点在平面直角坐标系的y轴上,则点P的坐标为 .
15.写出一个大于5的无理数 .
16.已知,用含x的代数式表示y,则 .
17.在平面直角坐标系中,已知点和点,若直线轴,则的值为 .
18.设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是 .①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是1;④存在实数x,使[x)-x=0.5成立.
三、解答题
19.已知是二元一次方程的一个解.
(1)求m的值;
(2)若x的取值范围如图所示,求y的正整数值.
20.在平面直角坐标系中,已知点,试分别根据下列条件,求出点的坐标.求:
(1)点在轴上;
(2)点的纵坐标比横坐标大3;
(3)点在过点,且与轴平行的直线上.
21.如图,已知:,,求的度数
22.已知方程组 与方程组 的解相同.求(2a+b)2004的值.
23.如图,△ABC,△CEF都是由△BDE经平移得到的像,A、C、F三点在同一条直线上.已知∠D=70°,∠BED=45°.
(1)BE=AF成立吗?请说明你的理由;
(2)求∠ECF的度数;
(3)△ECB可以看做是△BDE经过哪一种变换得到的(不需要说明理由).
24.如图,直线ABCD,直线EF分别交AB、CD于点M、N,∠CNF=40°,MG平分∠BMF,MG交CD于G,求∠EMB和∠MGN的度数.
25.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的关系,说明理由.
26.求方程2x+3y=5的整数解.
27.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数?
28.如图,已知直线,E,F分别是AB,CD上的点,点G在直线AB,CD内部,且,.
图1 图2 备用图
(1)求的度数.
(2)如图2,射线EG绕点E以每秒5°的速度逆时针旋转,交直线CD于点P,设运动时间为t秒().当时,试探究EP与GF的位置关系,并说明理由.
(3)在(2)中,射线FG绕点F同时以每秒10°的速度顺时针旋转得到射线FQ.当时,请直接写出t的值.
答案解析部分
1.【答案】C
【知识点】列二元一次方程组
2.【答案】B
【知识点】二元一次方程的解
3.【答案】C
【知识点】平行线的性质
4.【答案】A
【知识点】点的坐标
5.【答案】C
【知识点】点的坐标与象限的关系
6.【答案】D
【知识点】无理数的估值
7.【答案】D
【知识点】坐标与图形变化﹣平移
8.【答案】A
【知识点】二元一次方程的解
9.【答案】A
【知识点】无理数的大小比较
10.【答案】C
【知识点】角的运算;平行公理及推论;平行线的性质
11.【答案】-5或1
【知识点】坐标与图形性质
12.【答案】3
【知识点】点的坐标
13.【答案】
【知识点】平行线之间的距离
14.【答案】
【知识点】点的坐标
15.【答案】(答案不唯一)
【知识点】无理数的概念
16.【答案】
【知识点】二元一次方程的解
17.【答案】
【知识点】点的坐标
18.【答案】③④
【知识点】实数的运算
19.【答案】(1)
(2)1,2
【知识点】二元一次方程的解;二元一次方程组的解
20.【答案】(1)
(2)
(3)
【知识点】点的坐标;坐标与图形性质;一元一次方程的实际应用-几何问题
21.【答案】130°
【知识点】平行线的判定与性质
22.【答案】解:因为两个方程组的解相同,
所以解方程组 ,解得 .
代入另两个方程,得
解得 .
∴原式=(2×1﹣3)2004=1.
【知识点】二元一次方程组的解
23.【答案】解:(1)成立.
由平移的性质得:AC=BE,CF=BE.
又∵A、C、F三点在同一条直线上,
∴AF=AC+CF,
∴BE=(AC+CF)=AF;
(2)∵∠D=70°,∠BED=45°,
∴∠DBE=65°.
由平移的性质得:∠ECF=∠DBE=65°;
(3)△ECB可以看作由△BDE经过旋转变换而得到(或是通过对称、平移变换后得到).
【知识点】平移的性质
24.【答案】解:∵ABCD,
∴∠AMN=∠CNF=40°,
∴∠EMB=∠AMN=40°,
∴∠BMN=140°,
又∵MG平分∠BMF,
∴∠BMG=∠BMN=70°,
∵ABCD,
∴∠MGN=∠BMG=70°.
【知识点】平行线的性质;对顶角及其性质;邻补角;角平分线的概念
25.【答案】解:∠AED=∠C.
理由如下:
∵∠1+∠DFE=180°,
又∠1+∠2=180°,
∴∠2=∠DFE,
∴AB//EF,
∴∠3=∠ADE,
又∠3=∠B,
∴∠B=∠ADE,
∴DE//BC,
∴∠AED=∠C.
【知识点】角的运算;平行线的判定与性质
26.【答案】解:我们很容易发现,x=1,y=1是方程的一组解,
又因为(2,3)=1,由定理2,若a与b的最大公约数为1(即a与b互质),x0、y0为二元一次整系数不定方程ax+by=c的一组整数解(也称为特解),则ax+by=c的所有整数解(也称通解)为,
(k为任意整数).
方程的所有整数解为
,(k为任意整数).
【知识点】二元一次方程的解
27.【答案】解答:∵EF∥AD(已知) ∴∠2=∠3(两直线平行,同位角相等); ∵∠1=∠2(已知), ∴∠1=∠3(等量代换); ∴DG∥AB(内错角相等,两直线平行). ∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补). ∵∠BAC=70°, ∴∠AGD=110°
【知识点】平行线的性质
28.【答案】(1)解:如图1,过点G作.
图1
∵,
∴,
∴,,
∴.
(2)解:当时,,
∴,
∵,
∴,
∴,
∴.
(3)解:7或19
【知识点】平行线的判定与性质
21世纪教育网(www.21cnjy.com)
2 / 9
人教版数学(2024)七年级下册期中训练卷
一、单选题
1.“辉煌九秩,筑梦百年”,在巴蜀中学建校90周年之际,八年级学生王小明制作了一批手工艺品送给母校作纪念,每一件工艺品都包含一个礼盒和三张礼卡,已知材料可制作10个礼盒或50张礼卡,现有材料,并且制作出来的礼卡和礼盒刚好全部配套.设用材料用来制作礼盒,材料用来制作礼卡.则可列方程组( )
A. B.
C. D.
2.若是关于x、y的方程的一组解,则m的值为( )
A.—2 B.2 C.—4 D.4
3.如图,, , 若,那么的度数是( )
A. B. C. D.
4.在平面直角坐标系中到y轴的距离是( )
A.3 B.4 C.5 D.
5.点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.把无理数表示在数轴上,在这四个数中,被墨迹(如图所示)覆盖住的无理数是( )
A.8 B. C. D.
7.如图,将四边形先向右平移4个单位,再向上平移2个单位,那么点的对应点的坐标是( )
A. B. C. D.
8.若是关于、的方程的一个解,则的值是( )
A.5 B. C.8 D.
9.在实数四个数中,最小的是( )
A. B.-3.14 C. D.0
10.如图,AB∥CD,∠ABK的平分线BE的反向延长线和∠DCK的平分线CF的反向延长线相交于点H,∠K-∠H=27°,则∠K=( )
A.82° B.80° C.78° D.76°
二、填空题
11.在平面直角坐标系中,有点 ,点 ,当线段 轴,且 时,则 .
12.点A的坐标(4,-3),它到x轴的距离为
13.如图,在四边形中,,相交于点O,则与面积相等的三角形是 .
14.若点在平面直角坐标系的y轴上,则点P的坐标为 .
15.写出一个大于5的无理数 .
16.已知,用含x的代数式表示y,则 .
17.在平面直角坐标系中,已知点和点,若直线轴,则的值为 .
18.设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是 .①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是1;④存在实数x,使[x)-x=0.5成立.
三、解答题
19.已知是二元一次方程的一个解.
(1)求m的值;
(2)若x的取值范围如图所示,求y的正整数值.
20.在平面直角坐标系中,已知点,试分别根据下列条件,求出点的坐标.求:
(1)点在轴上;
(2)点的纵坐标比横坐标大3;
(3)点在过点,且与轴平行的直线上.
21.如图,已知:,,求的度数
22.已知方程组 与方程组 的解相同.求(2a+b)2004的值.
23.如图,△ABC,△CEF都是由△BDE经平移得到的像,A、C、F三点在同一条直线上.已知∠D=70°,∠BED=45°.
(1)BE=AF成立吗?请说明你的理由;
(2)求∠ECF的度数;
(3)△ECB可以看做是△BDE经过哪一种变换得到的(不需要说明理由).
24.如图,直线ABCD,直线EF分别交AB、CD于点M、N,∠CNF=40°,MG平分∠BMF,MG交CD于G,求∠EMB和∠MGN的度数.
25.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的关系,说明理由.
26.求方程2x+3y=5的整数解.
27.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数?
28.如图,已知直线,E,F分别是AB,CD上的点,点G在直线AB,CD内部,且,.
图1 图2 备用图
(1)求的度数.
(2)如图2,射线EG绕点E以每秒5°的速度逆时针旋转,交直线CD于点P,设运动时间为t秒().当时,试探究EP与GF的位置关系,并说明理由.
(3)在(2)中,射线FG绕点F同时以每秒10°的速度顺时针旋转得到射线FQ.当时,请直接写出t的值.
答案解析部分
1.【答案】C
【知识点】列二元一次方程组
2.【答案】B
【知识点】二元一次方程的解
3.【答案】C
【知识点】平行线的性质
4.【答案】A
【知识点】点的坐标
5.【答案】C
【知识点】点的坐标与象限的关系
6.【答案】D
【知识点】无理数的估值
7.【答案】D
【知识点】坐标与图形变化﹣平移
8.【答案】A
【知识点】二元一次方程的解
9.【答案】A
【知识点】无理数的大小比较
10.【答案】C
【知识点】角的运算;平行公理及推论;平行线的性质
11.【答案】-5或1
【知识点】坐标与图形性质
12.【答案】3
【知识点】点的坐标
13.【答案】
【知识点】平行线之间的距离
14.【答案】
【知识点】点的坐标
15.【答案】(答案不唯一)
【知识点】无理数的概念
16.【答案】
【知识点】二元一次方程的解
17.【答案】
【知识点】点的坐标
18.【答案】③④
【知识点】实数的运算
19.【答案】(1)
(2)1,2
【知识点】二元一次方程的解;二元一次方程组的解
20.【答案】(1)
(2)
(3)
【知识点】点的坐标;坐标与图形性质;一元一次方程的实际应用-几何问题
21.【答案】130°
【知识点】平行线的判定与性质
22.【答案】解:因为两个方程组的解相同,
所以解方程组 ,解得 .
代入另两个方程,得
解得 .
∴原式=(2×1﹣3)2004=1.
【知识点】二元一次方程组的解
23.【答案】解:(1)成立.
由平移的性质得:AC=BE,CF=BE.
又∵A、C、F三点在同一条直线上,
∴AF=AC+CF,
∴BE=(AC+CF)=AF;
(2)∵∠D=70°,∠BED=45°,
∴∠DBE=65°.
由平移的性质得:∠ECF=∠DBE=65°;
(3)△ECB可以看作由△BDE经过旋转变换而得到(或是通过对称、平移变换后得到).
【知识点】平移的性质
24.【答案】解:∵ABCD,
∴∠AMN=∠CNF=40°,
∴∠EMB=∠AMN=40°,
∴∠BMN=140°,
又∵MG平分∠BMF,
∴∠BMG=∠BMN=70°,
∵ABCD,
∴∠MGN=∠BMG=70°.
【知识点】平行线的性质;对顶角及其性质;邻补角;角平分线的概念
25.【答案】解:∠AED=∠C.
理由如下:
∵∠1+∠DFE=180°,
又∠1+∠2=180°,
∴∠2=∠DFE,
∴AB//EF,
∴∠3=∠ADE,
又∠3=∠B,
∴∠B=∠ADE,
∴DE//BC,
∴∠AED=∠C.
【知识点】角的运算;平行线的判定与性质
26.【答案】解:我们很容易发现,x=1,y=1是方程的一组解,
又因为(2,3)=1,由定理2,若a与b的最大公约数为1(即a与b互质),x0、y0为二元一次整系数不定方程ax+by=c的一组整数解(也称为特解),则ax+by=c的所有整数解(也称通解)为,
(k为任意整数).
方程的所有整数解为
,(k为任意整数).
【知识点】二元一次方程的解
27.【答案】解答:∵EF∥AD(已知) ∴∠2=∠3(两直线平行,同位角相等); ∵∠1=∠2(已知), ∴∠1=∠3(等量代换); ∴DG∥AB(内错角相等,两直线平行). ∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补). ∵∠BAC=70°, ∴∠AGD=110°
【知识点】平行线的性质
28.【答案】(1)解:如图1,过点G作.
图1
∵,
∴,
∴,,
∴.
(2)解:当时,,
∴,
∵,
∴,
∴,
∴.
(3)解:7或19
【知识点】平行线的判定与性质
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
