北师大版五年级数学上册期末高频易错题综合检测卷四(含解析)
文档属性
| 名称 | 北师大版五年级数学上册期末高频易错题综合检测卷四(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 255.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版五年级数学上册期末高频易错题综合检测卷四
一、选择题(共16分)
1.下列各式中,结果大于1的是( )。
A.1×0.9 B.0.9÷1 C.1÷0.9 D.1÷2.5
2.下列图形中,( )不是轴对称图形。
A. B. C.D.
3.下列几组数中,全都是质数的是( )。
A.1、5、17、51 B.2、15、31、57 C.3、19、61、23 D.11、91、81、71
4.如图,在两条平行线间有三个不同的图形,它们的面积大小关系是( )。
A.①>②>③ B.②>③>① C.②>①>③ D.③>①>②
5.一些三位数被3,5,7除都余1,把这些三位数从小到大排成一排,其中第5个数是( )
A.106 B.524 C.525 D.526
6.在下面同样大小的大正方形中,阴影部分面积最大的是( )。
A. B. C. D.
7.下面每个小方格的边长表示1cm,左边图形的面积约是( )cm2,右边图形的面积是( )cm2。
A.8;10 B.10;17 C.15;8 D.20;17
8.甲乙两人用一个转盘(如下图)做游戏,如果指针停在符合要求的数上,则获胜,反之失败。若想使获胜的可能性最大,应该采用选项( )。
A.质数 B.合数 C.2的倍数 D.36的因数
二、填空题(共16分)
9.盒子里有完全相同的10个黄球和7个白球,再放入( )个白球,摸到白球和黄球的可能性相等。
10.19.74÷2.8的商保留整数是( ),保留一位小数是( ).
11.想一想下面的每幅图是怎样得到的,填一填。
(1)通过平移得到的图案有( )。
(2)通过轴对称得到的图案有( )。
12.要让25×15×□这道算式乘积的末尾有3个零,□最小填( )。
13.佳源超市每千克西兰花售价为9.98元,王阿姨买了2.2千克,用微信付款,需要付( )元钱。
14.世纪广场有一块面积是180平方米的平行四边形草地,这块草地的高是12米,这条高对应的底是( )米。
15.星星制衣厂女工人数比男工人数多。应把( )看作一个整体,女工人数是男工的( )。
16.在一个长30dm,宽24dm的房间地面上铺正方形地砖,为了确保不浪费,正方形地砖的边长最长是( )分米,一共需要( )块地砖。(地砖的边长要求是整分米数)
三、判断题(共8分)
17.,左图中图②向上平移2格可以得到图①。( )
18.一个平行四边形的鱼塘,底是300m,对应的高是200m,这个平行四边形鱼塘的面积是。( )
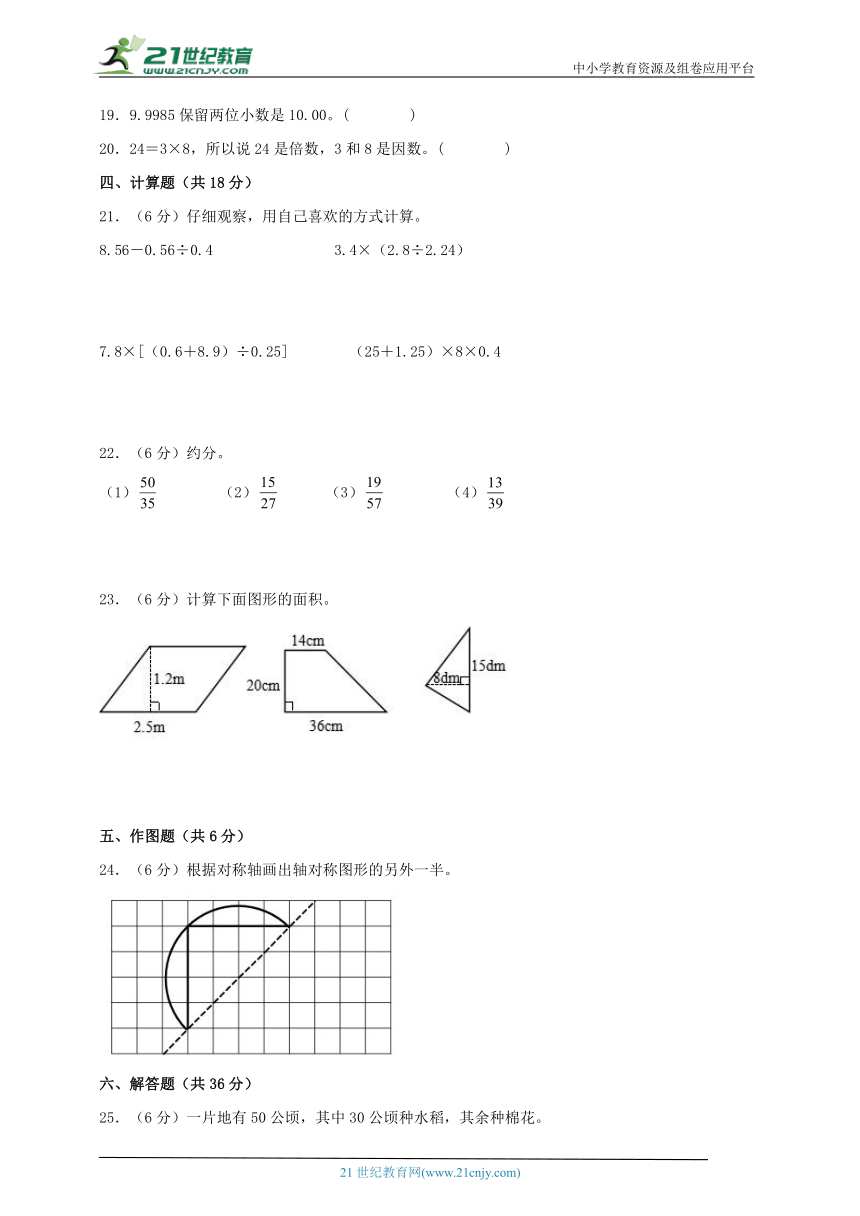
19.9.9985保留两位小数是10.00。( )
20.24=3×8,所以说24是倍数,3和8是因数。( )
四、计算题(共18分)
21.(6分)仔细观察,用自己喜欢的方式计算。
8.56-0.56÷0.4 3.4×(2.8÷2.24)
7.8×[(0.6+8.9)÷0.25] (25+1.25)×8×0.4
22.(6分)约分。
(1) (2) (3) (4)
23.(6分)计算下面图形的面积。
五、作图题(共6分)
24.(6分)根据对称轴画出轴对称图形的另外一半。
六、解答题(共36分)
25.(6分)一片地有50公顷,其中30公顷种水稻,其余种棉花。
①种水稻的面积占总面积的几分之几?
②种棉花的面积占总面积的几分之几?
③种棉花的面积占水稻的面积的几分之几?
26.(6分)做一个生日蛋糕需要0.15kg鲜奶油,13kg鲜奶油最多可以做多少个这种生日蛋糕?
27.(6分)李伯伯家的一棵石榴树收获了76个石榴,他每5个装一袋,能正好装完吗?每2个装一袋,能正好装完吗?为什么?
28.(6分)学校要制作一些锦旗,锦旗式样如图所示,制作一面锦旗至少需要多少平方厘米的布料?
29.(6分)有白球和黑球各若干,在布袋里放6个,怎样放才可能符合题意?
(1)任意摸出一个球,不可能是黑球。
(2)任意摸出一个球,一定是黑球。
(3)摸多次,经常摸到白球。
(4)摸多次,偶尔摸到白球。
30.(6分)秦朝末年、楚汉相争。一次,韩信带领1500名将士与楚王大将李锋交战。苦战一场,楚军不敌,败退回营,汉军也死伤四五百人,于是韩信整顿兵马也返回大本营。当行至一山坡,忽有后军来报,说有楚军骑兵追来。只见远方尘土飞扬,杀声震天。汉军本来已十分疲惫,这时队伍大哗。韩信兵马到坡顶,见来敌不足五百骑,便点兵迎敌。他命令士兵30人一排,结果多出2名;接着命令士兵50人一排,结果多出2名;他又命令士兵70人一排,结果又多出2名。请你算一算韩信此时有多少名士兵?
参考答案
1.C
【分析】根据小数的乘除法运算法则计算出得数,然后比较即可。
【详解】A.因为1×0.9=0.9,0.9<1,该选项不符合;
B.因为0.9÷1=0.9,0.9<1,该选项不符合;
C.因为1÷0.9=1.11…,1.11…>1,该选项符合;
D.因为1÷2.5=0.4,0.4<1,该选项不符合;
故答案为:C
【点睛】本题主要考查小数乘、除法的计算方法,也可根据因数与积、被除数与商的关系进行解答。
2.C
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】A.是轴对称图形;
B.是轴对称图形;
C.不是轴对称图形;
D.是轴对称图形。
故答案为:C
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
3.C
【分析】除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。
【详解】A.1、5、17、51,1不是质数;
B.2、15、31、57,15、57不是质数,是合数;
C.3、19、61、23,都是质数;
D.11、91、81、71,91、81是合数,不是质数;
故答案为:C
【点睛】关键是理解质数、合数的分类标准。
4.C
【分析】根据图可知,三个图形的高都相等,可以假设它们的高是8厘米,根据三角形的面积公式:底×高÷2;平行四边形的面积公式:底×高,梯形的面积公式:(上底+下底)×高÷2,把数代入公式即可求出它们的面积,之后再进行比较即可。
【详解】假设它们的高是8厘米;
三角形的面积:8×8÷2
=64÷2
=32(平方厘米)
平行四边形的面积:8×5=40(平方厘米)
梯形的面积:(2+4)×8÷2
=6×8÷2
=48÷2
=24(平方厘米)
24<32<40
所以平行四边形的面积>三角形的面积>梯形的面积。
故答案为:C
【点睛】本题主要考查平行四边形、三角形、梯形的面积公式,熟练掌握它们的面积公式并灵活运用。
5.D
【详解】试题分析:因为3、5、7最小公倍数105,那么这些3位数就是n倍的105再加上1,所以第5个应该是5×105+1解答即可.
解:因为3、5、7是互质数,所以三个数的最小公倍数为;3×5×7=105,
第从小到大排成一排,五个数为:105×5+1=526;
故选D.
点评:解答此题应结合题意,根据求几个数的最小公倍数的方法进行解答即可.
6.C
【分析】根据分数的意义:把单位“1”平均分成若干份,表示其中的一份或几份的数叫做分数,先把每个选项的阴影部分面积占大正方形的面积的分数表示出来,再进行比较大小,即可解答。
【详解】A.阴影部分面积占大正方形面积的;
B.阴影部分面积占大正方形面积的=;
C.阴影部分面积占大正方形面积的;
D.阴影部分面积占大正方形面积的
=;
=
=
>>
C图的阴影部分面积最大。
故答案选:C
【点睛】本题考查分数的意义,以及分数比较大小的方法。
7.C
【分析】利用数方格的方法,先数整格,再数不满一格的,不满一格的按半格算,最后把两次的结果相加求和;据此解答。
【详解】由分析得:
左边图形的面积:
10+10÷2
=10+5
=15(cm2)
右边图形的面积:
6+4÷2
=6+2
=8(cm2)
左边图形的面积是15cm2,右边图形的面积是8cm2。
故答案为:C
【点睛】此题考查的目的是理解掌握不规则图形面积的计算方法及应用。
8.D
【分析】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种数的数量多,发生的可能性就大一些,据此分析。
【详解】A.质数有2、3、5、7,共4个;
B.合数有4、6、8、9、10,共5个;
C.2的倍数有2、4、6、8、10,共5个;
D.36的因数有1、2、3、4、6、9,共6个。
故答案为:D
【点睛】关键是掌握2的倍数的特征,理解质数、合数的分类标准,会找一个数的因数,再根据可能性大小的判断方法进行分析。
9.3
【分析】事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。所以要使摸到白球和黄球的可能性相等,则黄球和白球的数量相等即可,据此解答。
【详解】10-7=3(个)
所以再放入3个白球,摸到白球和黄球的可能性相等。
【点睛】本题考查可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
10. 7 7.1
【分析】根据小数除法的计算方法,求出算式的结果,再根据四舍五入法保留相应的小数位数。保留整数,就看这个小数的第一位,保留一位小数,就看这个小数的第二位,运用“四舍五入”的方法取近似值即可解答。
【详解】19.74÷2.8=7.05
7.05≈7.1
7.05≈7
所以,19.74÷2.8的商保留整数是7,保留一位小数是7.1。
【点睛】此题主要考查运用“四舍五入”法取近似值:要看精确到哪一位,从它的下一位运用“四舍五入”取值。
11.(1)①③
(2)②③④
【分析】在平面内,将一个图形上所有的点都按照某个方向作相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移;如果一个图形沿一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形;所以①是通过平移得到的图案,②是通过轴对称得到的图案,③是既可以通过平移也可以通过轴对称得到的图案,④是通过轴对称得到的图案。
【详解】(1)通过平移得到的图案有①③
(2)通过轴对称得到的图案有②③④
【点睛】本题考查平移和轴对称的应用,理解平移和轴对称的意义是关键。
12.8
【分析】两个数相乘,如果积的末尾是零,是因为两个因数中含有因数5与因数2,因数5与因数2相乘,积末尾就会出现1个零(5×2=10),将25×15改写为5×5×5×3,5×5×5×3中有3个5,要使乘积的末尾有3个零,则需要与3个2相乘;据此解答。
【详解】由分析可得:要让25×15×□这道算式乘积的末尾有3个零,□最小填2×2×2=8。
【点睛】理解“两个数相乘,如果积的末尾是零,是因为两个因数中含有因数5与因数2”是解题的关键。
13.21.96
【分析】根据单价×数量=总价,用9.98乘2.2即可求解,因为付钱时只能到分,所以结果要保留两位小数。
【详解】9.98×2.2=21.956(元)≈21.96(元)
则需要付21.96元钱。
【点睛】本题考查小数乘法,明确单价、数量和总价之间的关系是解题的关键。
14.15
【分析】已知平行四边形草地的面积和高,根据平行四边形的底=面积÷高,即可求出这条高对应的底。
【详解】180÷12=15(米)
这条高对应的底是15米。
15. 男工人数 /
【分析】根据判断单位“1”的方法:一般是把比、占、是、相当于,后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”,进行解答即可。
【详解】1+=
则星星制衣厂女工人数比男工人数多。应把男工人数看作一个整体,女工人数是男工的。
16. 6 20
【分析】根据题意,正方形地砖把房间的地面铺满,则地砖的边长是长、宽的公因数;地砖的最大边长就是长、宽的最大公因数:30、24分解质因数后,把公有的相同质因数乘起来就是最大公因数,即可求出地砖的最大边长。再看长、宽分别有几个这样的最大公因数,最后相乘,求出地砖的块数。
【详解】30=2×3×5
24=2×2×2×3
30和24的最大公因数是:2×3=6
即正方形地砖的边长最大是6分米。
30÷6=5(块)
24÷6=4(块)
5×4=20(块)
一共需要20块地砖。
【点睛】明确长、宽的最大公因数是正方形地砖的最大边长是解题的关键。
17.√
【分析】找出图②到图①的对应点平移的方向和格数即可。
【详解】观察图形可知,图②向上平移2格可以得到图①,原题说法正确。
故答案为:√
【点睛】此题考查了图形的平移,关键是找准对应点平移的方向和格数。
18.√
【分析】平行四边形的面积=底×高,据此代入数据求出平行四边形鱼塘的面积并判断即可。
【详解】300×200=60000(m2)
故答案为:√
【点睛】掌握平行四边形的面积公式是解答本题的关键。
19.√
【分析】保留两位小数,即精确到百分位,看小数点后面第三位,利用“四舍五入”法解答即可。
【详解】9.9985千分位上是8,8>5,向百分位进1,百分位上的9加进上来的1是10,向十分位进1,十分位上的9加进上来的1是10,向个位进1,个位上的9加进上来的1是10,向十位进1,所以9.9985保留两位小数是10.00。即原题说法正确。
故答案为:√
20.×
【分析】根据倍数和因数的定义可知,如果a×b=c(a、b、c都是非0的自然数)那么a和b就是c的因数,c就是a和b的倍数;因数和倍数两个不同的概念是相互依存的,不能单独存在,据此分析。
【详解】由分析可知:
24=3×8,所以说24是3和8的倍数,3和8是24的因数。原题干说法错误。
故答案为:×
21.7.16;4.25
296.4;84
【分析】先算除法,再算减法;
先算小括号里面的除法,再算括号外面的乘法;
先算小括号里的加法,再算中括号里的除法,最后算括号外的乘法;
根据乘法分配律和乘法交换律简算即可。
【详解】8.56-0.56÷0.4
=8.56-1.4
=7.16
3.4×(2.8÷2.24)
=3.4×1.25
=4.25
7.8×[(0.6+8.9)÷0.25]
=7.8×[9.5÷0.25]
=7.8×38
=296.4
(25+1.25)×8×0.4
=25×8×0.4+1.25×8×0.4
=25×0.4×8+1.25×8×0.4
=10×8+10×0.4
=80+4
=84
22.(1);(2);(3);(4)
【分析】根据分数的基本性质:分数的分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,据此解答。
【详解】(1)
(2)
(3)
(4)
23.3平方米;500平方厘米;60平方分米
【分析】根据平行四边形的面积=底×高,代入数值进行计算即可;
根据梯形的面积=(上底+下底)×高÷2,代入数值进行计算即可;
根据三角形的面积=底×高÷2,代入数值进行计算即可。
【详解】1.2×2.5=3(平方米)
(14+36)×20÷2
=50×20÷2
=1000÷2
=50(平方厘米)
15×8÷2
=120÷2
=60(平方分米)
24.见详解
【分析】根据轴对称图形的性质,先找到右边图形各关键点的对应点,依次连接各点即可画出图形的另一半,使它成为一个轴对称图形。
【详解】
【点睛】掌握补全轴对称图形的步骤和方法是解题的关键。
25.【分析】①求种水稻的面积占总面积的几分之几,用种水稻的面积÷总面积即可;
②求种棉花的面积占总面积的几分之几,用种棉花的面积÷总面积即可;
③求种棉花的面积占水稻的面积的几分之几,用种棉花的面积÷水稻的面积即可。
【详解】①30÷50=
答:种水稻的面积占总面积的。
②(50-30)÷50
=20÷50
=
答:种棉花的面积占总面积的。
③(50-30)÷30
=20÷30
=
答:种棉花的面积占水稻的面积的。
【点睛】求一个数是(占)另一个数的几分之几,用除法。
26.86个
【分析】用13kg除以每个生日蛋糕的鲜牛奶的质量,求出可以做的蛋糕的数量,剩下的鲜牛奶不够做一个,用去尾法解决即可。
【详解】13÷0.15=86(个)……0.1(kg)≈86(个)
答:13kg鲜奶油最多可以做86个这种生日蛋糕。
【点睛】本题考查商的近似数,解答本题的关键是掌握用去尾法解决问题的计算方法。
27.见详解
【分析】根据能被2整除的数的特征和能被5整除的数的特征进行解答。
【详解】76个石榴,每5个装一袋,不能正好装完;每2个装一袋,能正好装完;因为76不是5的倍数,是2的倍数。
【点睛】此题考查的是能被2和5整除的数的特征的知识的应用。
28.1575平方厘米
【分析】可以把这个锦旗看作是一个长是60厘米,宽是30厘米的长方形面积减去下面的小三角形的面积,三角形的底是30厘米,高是:60-45=15(厘米),根据三角形的面积公式:底×高÷2,长方形的面积公式:长×宽,把数代入公式即可求解。
【详解】如图:
=1800-30×15÷2
=1800-225
(平方厘米)
答:制作一面锦旗至少需要1575平方厘米的布料。
【点睛】本题主要考查组合图形的面积的求法,可以把组合图形分成规则图形计算,同时熟练掌握规则图形的面积公式是解题的关键。
29.(1)6个球都是白球
(2)6个球都是黑球
(3)5个白球,1个黑球
(4)5个黑球,1个白球
【分析】(1)要使摸出的不可能是黑球,则盒子中没有黑球;
(2)要使摸出的一定是黑球,则盒子中只有6黑球;
(3)要使摸出白球的可能性大,则盒子中白球的数量最多,可放5个白球,1个黑球;
(4)要使摸出白球的可能性小,则盒子中白球的数量最少,可放5个黑球,1个白球。
【详解】(1)任意摸出一个球,不可能是黑球,即放入的6个球都是白球;
(2)任意摸出一个球,一定是黑球,放入的6个球都是黑球;
(3)摸多次,经常摸到白球,说明白球放得多,可以放5个白球,1个黑球;
(4)摸多次,偶尔摸到白球,说明放的白球少,可以放5个黑球,1个白球。
【点睛】本题考查了可能性,袋子中哪种颜色的球多,摸出的可能性就大。
30.1052名
【分析】士兵30人、50人或70人一排,结果都多出2名,则此时士兵的数量比30、50和70的公倍数多2。根据题意,韩信带领1500名将士与楚王大将李锋交战,汉军死伤四五百人,则剩下的士兵大约是1000名。先求出30、50和70的公倍数,再从中找出接近1000的数,最后加上2,就是韩信此时有士兵的数量。
用质因数分解法求几个数的最小公倍数,全部公有的质因数和各自独立的质因数,它们连乘的积就是这几个数的最小公倍数。再用最小公倍数分别乘2、3、4…,即可求出其他的公倍数。
【详解】30=3×2×5
50=5×2×5
70=7×2×5
30、50和70的最小公倍数是2×5×3×5×7=1050。
1050+2=1052(名)
答:韩信此时有1052名士兵。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版五年级数学上册期末高频易错题综合检测卷四
一、选择题(共16分)
1.下列各式中,结果大于1的是( )。
A.1×0.9 B.0.9÷1 C.1÷0.9 D.1÷2.5
2.下列图形中,( )不是轴对称图形。
A. B. C.D.
3.下列几组数中,全都是质数的是( )。
A.1、5、17、51 B.2、15、31、57 C.3、19、61、23 D.11、91、81、71
4.如图,在两条平行线间有三个不同的图形,它们的面积大小关系是( )。
A.①>②>③ B.②>③>① C.②>①>③ D.③>①>②
5.一些三位数被3,5,7除都余1,把这些三位数从小到大排成一排,其中第5个数是( )
A.106 B.524 C.525 D.526
6.在下面同样大小的大正方形中,阴影部分面积最大的是( )。
A. B. C. D.
7.下面每个小方格的边长表示1cm,左边图形的面积约是( )cm2,右边图形的面积是( )cm2。
A.8;10 B.10;17 C.15;8 D.20;17
8.甲乙两人用一个转盘(如下图)做游戏,如果指针停在符合要求的数上,则获胜,反之失败。若想使获胜的可能性最大,应该采用选项( )。
A.质数 B.合数 C.2的倍数 D.36的因数
二、填空题(共16分)
9.盒子里有完全相同的10个黄球和7个白球,再放入( )个白球,摸到白球和黄球的可能性相等。
10.19.74÷2.8的商保留整数是( ),保留一位小数是( ).
11.想一想下面的每幅图是怎样得到的,填一填。
(1)通过平移得到的图案有( )。
(2)通过轴对称得到的图案有( )。
12.要让25×15×□这道算式乘积的末尾有3个零,□最小填( )。
13.佳源超市每千克西兰花售价为9.98元,王阿姨买了2.2千克,用微信付款,需要付( )元钱。
14.世纪广场有一块面积是180平方米的平行四边形草地,这块草地的高是12米,这条高对应的底是( )米。
15.星星制衣厂女工人数比男工人数多。应把( )看作一个整体,女工人数是男工的( )。
16.在一个长30dm,宽24dm的房间地面上铺正方形地砖,为了确保不浪费,正方形地砖的边长最长是( )分米,一共需要( )块地砖。(地砖的边长要求是整分米数)
三、判断题(共8分)
17.,左图中图②向上平移2格可以得到图①。( )
18.一个平行四边形的鱼塘,底是300m,对应的高是200m,这个平行四边形鱼塘的面积是。( )
19.9.9985保留两位小数是10.00。( )
20.24=3×8,所以说24是倍数,3和8是因数。( )
四、计算题(共18分)
21.(6分)仔细观察,用自己喜欢的方式计算。
8.56-0.56÷0.4 3.4×(2.8÷2.24)
7.8×[(0.6+8.9)÷0.25] (25+1.25)×8×0.4
22.(6分)约分。
(1) (2) (3) (4)
23.(6分)计算下面图形的面积。
五、作图题(共6分)
24.(6分)根据对称轴画出轴对称图形的另外一半。
六、解答题(共36分)
25.(6分)一片地有50公顷,其中30公顷种水稻,其余种棉花。
①种水稻的面积占总面积的几分之几?
②种棉花的面积占总面积的几分之几?
③种棉花的面积占水稻的面积的几分之几?
26.(6分)做一个生日蛋糕需要0.15kg鲜奶油,13kg鲜奶油最多可以做多少个这种生日蛋糕?
27.(6分)李伯伯家的一棵石榴树收获了76个石榴,他每5个装一袋,能正好装完吗?每2个装一袋,能正好装完吗?为什么?
28.(6分)学校要制作一些锦旗,锦旗式样如图所示,制作一面锦旗至少需要多少平方厘米的布料?
29.(6分)有白球和黑球各若干,在布袋里放6个,怎样放才可能符合题意?
(1)任意摸出一个球,不可能是黑球。
(2)任意摸出一个球,一定是黑球。
(3)摸多次,经常摸到白球。
(4)摸多次,偶尔摸到白球。
30.(6分)秦朝末年、楚汉相争。一次,韩信带领1500名将士与楚王大将李锋交战。苦战一场,楚军不敌,败退回营,汉军也死伤四五百人,于是韩信整顿兵马也返回大本营。当行至一山坡,忽有后军来报,说有楚军骑兵追来。只见远方尘土飞扬,杀声震天。汉军本来已十分疲惫,这时队伍大哗。韩信兵马到坡顶,见来敌不足五百骑,便点兵迎敌。他命令士兵30人一排,结果多出2名;接着命令士兵50人一排,结果多出2名;他又命令士兵70人一排,结果又多出2名。请你算一算韩信此时有多少名士兵?
参考答案
1.C
【分析】根据小数的乘除法运算法则计算出得数,然后比较即可。
【详解】A.因为1×0.9=0.9,0.9<1,该选项不符合;
B.因为0.9÷1=0.9,0.9<1,该选项不符合;
C.因为1÷0.9=1.11…,1.11…>1,该选项符合;
D.因为1÷2.5=0.4,0.4<1,该选项不符合;
故答案为:C
【点睛】本题主要考查小数乘、除法的计算方法,也可根据因数与积、被除数与商的关系进行解答。
2.C
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】A.是轴对称图形;
B.是轴对称图形;
C.不是轴对称图形;
D.是轴对称图形。
故答案为:C
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
3.C
【分析】除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。
【详解】A.1、5、17、51,1不是质数;
B.2、15、31、57,15、57不是质数,是合数;
C.3、19、61、23,都是质数;
D.11、91、81、71,91、81是合数,不是质数;
故答案为:C
【点睛】关键是理解质数、合数的分类标准。
4.C
【分析】根据图可知,三个图形的高都相等,可以假设它们的高是8厘米,根据三角形的面积公式:底×高÷2;平行四边形的面积公式:底×高,梯形的面积公式:(上底+下底)×高÷2,把数代入公式即可求出它们的面积,之后再进行比较即可。
【详解】假设它们的高是8厘米;
三角形的面积:8×8÷2
=64÷2
=32(平方厘米)
平行四边形的面积:8×5=40(平方厘米)
梯形的面积:(2+4)×8÷2
=6×8÷2
=48÷2
=24(平方厘米)
24<32<40
所以平行四边形的面积>三角形的面积>梯形的面积。
故答案为:C
【点睛】本题主要考查平行四边形、三角形、梯形的面积公式,熟练掌握它们的面积公式并灵活运用。
5.D
【详解】试题分析:因为3、5、7最小公倍数105,那么这些3位数就是n倍的105再加上1,所以第5个应该是5×105+1解答即可.
解:因为3、5、7是互质数,所以三个数的最小公倍数为;3×5×7=105,
第从小到大排成一排,五个数为:105×5+1=526;
故选D.
点评:解答此题应结合题意,根据求几个数的最小公倍数的方法进行解答即可.
6.C
【分析】根据分数的意义:把单位“1”平均分成若干份,表示其中的一份或几份的数叫做分数,先把每个选项的阴影部分面积占大正方形的面积的分数表示出来,再进行比较大小,即可解答。
【详解】A.阴影部分面积占大正方形面积的;
B.阴影部分面积占大正方形面积的=;
C.阴影部分面积占大正方形面积的;
D.阴影部分面积占大正方形面积的
=;
=
=
>>
C图的阴影部分面积最大。
故答案选:C
【点睛】本题考查分数的意义,以及分数比较大小的方法。
7.C
【分析】利用数方格的方法,先数整格,再数不满一格的,不满一格的按半格算,最后把两次的结果相加求和;据此解答。
【详解】由分析得:
左边图形的面积:
10+10÷2
=10+5
=15(cm2)
右边图形的面积:
6+4÷2
=6+2
=8(cm2)
左边图形的面积是15cm2,右边图形的面积是8cm2。
故答案为:C
【点睛】此题考查的目的是理解掌握不规则图形面积的计算方法及应用。
8.D
【分析】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种数的数量多,发生的可能性就大一些,据此分析。
【详解】A.质数有2、3、5、7,共4个;
B.合数有4、6、8、9、10,共5个;
C.2的倍数有2、4、6、8、10,共5个;
D.36的因数有1、2、3、4、6、9,共6个。
故答案为:D
【点睛】关键是掌握2的倍数的特征,理解质数、合数的分类标准,会找一个数的因数,再根据可能性大小的判断方法进行分析。
9.3
【分析】事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。所以要使摸到白球和黄球的可能性相等,则黄球和白球的数量相等即可,据此解答。
【详解】10-7=3(个)
所以再放入3个白球,摸到白球和黄球的可能性相等。
【点睛】本题考查可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
10. 7 7.1
【分析】根据小数除法的计算方法,求出算式的结果,再根据四舍五入法保留相应的小数位数。保留整数,就看这个小数的第一位,保留一位小数,就看这个小数的第二位,运用“四舍五入”的方法取近似值即可解答。
【详解】19.74÷2.8=7.05
7.05≈7.1
7.05≈7
所以,19.74÷2.8的商保留整数是7,保留一位小数是7.1。
【点睛】此题主要考查运用“四舍五入”法取近似值:要看精确到哪一位,从它的下一位运用“四舍五入”取值。
11.(1)①③
(2)②③④
【分析】在平面内,将一个图形上所有的点都按照某个方向作相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移;如果一个图形沿一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形;所以①是通过平移得到的图案,②是通过轴对称得到的图案,③是既可以通过平移也可以通过轴对称得到的图案,④是通过轴对称得到的图案。
【详解】(1)通过平移得到的图案有①③
(2)通过轴对称得到的图案有②③④
【点睛】本题考查平移和轴对称的应用,理解平移和轴对称的意义是关键。
12.8
【分析】两个数相乘,如果积的末尾是零,是因为两个因数中含有因数5与因数2,因数5与因数2相乘,积末尾就会出现1个零(5×2=10),将25×15改写为5×5×5×3,5×5×5×3中有3个5,要使乘积的末尾有3个零,则需要与3个2相乘;据此解答。
【详解】由分析可得:要让25×15×□这道算式乘积的末尾有3个零,□最小填2×2×2=8。
【点睛】理解“两个数相乘,如果积的末尾是零,是因为两个因数中含有因数5与因数2”是解题的关键。
13.21.96
【分析】根据单价×数量=总价,用9.98乘2.2即可求解,因为付钱时只能到分,所以结果要保留两位小数。
【详解】9.98×2.2=21.956(元)≈21.96(元)
则需要付21.96元钱。
【点睛】本题考查小数乘法,明确单价、数量和总价之间的关系是解题的关键。
14.15
【分析】已知平行四边形草地的面积和高,根据平行四边形的底=面积÷高,即可求出这条高对应的底。
【详解】180÷12=15(米)
这条高对应的底是15米。
15. 男工人数 /
【分析】根据判断单位“1”的方法:一般是把比、占、是、相当于,后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”,进行解答即可。
【详解】1+=
则星星制衣厂女工人数比男工人数多。应把男工人数看作一个整体,女工人数是男工的。
16. 6 20
【分析】根据题意,正方形地砖把房间的地面铺满,则地砖的边长是长、宽的公因数;地砖的最大边长就是长、宽的最大公因数:30、24分解质因数后,把公有的相同质因数乘起来就是最大公因数,即可求出地砖的最大边长。再看长、宽分别有几个这样的最大公因数,最后相乘,求出地砖的块数。
【详解】30=2×3×5
24=2×2×2×3
30和24的最大公因数是:2×3=6
即正方形地砖的边长最大是6分米。
30÷6=5(块)
24÷6=4(块)
5×4=20(块)
一共需要20块地砖。
【点睛】明确长、宽的最大公因数是正方形地砖的最大边长是解题的关键。
17.√
【分析】找出图②到图①的对应点平移的方向和格数即可。
【详解】观察图形可知,图②向上平移2格可以得到图①,原题说法正确。
故答案为:√
【点睛】此题考查了图形的平移,关键是找准对应点平移的方向和格数。
18.√
【分析】平行四边形的面积=底×高,据此代入数据求出平行四边形鱼塘的面积并判断即可。
【详解】300×200=60000(m2)
故答案为:√
【点睛】掌握平行四边形的面积公式是解答本题的关键。
19.√
【分析】保留两位小数,即精确到百分位,看小数点后面第三位,利用“四舍五入”法解答即可。
【详解】9.9985千分位上是8,8>5,向百分位进1,百分位上的9加进上来的1是10,向十分位进1,十分位上的9加进上来的1是10,向个位进1,个位上的9加进上来的1是10,向十位进1,所以9.9985保留两位小数是10.00。即原题说法正确。
故答案为:√
20.×
【分析】根据倍数和因数的定义可知,如果a×b=c(a、b、c都是非0的自然数)那么a和b就是c的因数,c就是a和b的倍数;因数和倍数两个不同的概念是相互依存的,不能单独存在,据此分析。
【详解】由分析可知:
24=3×8,所以说24是3和8的倍数,3和8是24的因数。原题干说法错误。
故答案为:×
21.7.16;4.25
296.4;84
【分析】先算除法,再算减法;
先算小括号里面的除法,再算括号外面的乘法;
先算小括号里的加法,再算中括号里的除法,最后算括号外的乘法;
根据乘法分配律和乘法交换律简算即可。
【详解】8.56-0.56÷0.4
=8.56-1.4
=7.16
3.4×(2.8÷2.24)
=3.4×1.25
=4.25
7.8×[(0.6+8.9)÷0.25]
=7.8×[9.5÷0.25]
=7.8×38
=296.4
(25+1.25)×8×0.4
=25×8×0.4+1.25×8×0.4
=25×0.4×8+1.25×8×0.4
=10×8+10×0.4
=80+4
=84
22.(1);(2);(3);(4)
【分析】根据分数的基本性质:分数的分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,据此解答。
【详解】(1)
(2)
(3)
(4)
23.3平方米;500平方厘米;60平方分米
【分析】根据平行四边形的面积=底×高,代入数值进行计算即可;
根据梯形的面积=(上底+下底)×高÷2,代入数值进行计算即可;
根据三角形的面积=底×高÷2,代入数值进行计算即可。
【详解】1.2×2.5=3(平方米)
(14+36)×20÷2
=50×20÷2
=1000÷2
=50(平方厘米)
15×8÷2
=120÷2
=60(平方分米)
24.见详解
【分析】根据轴对称图形的性质,先找到右边图形各关键点的对应点,依次连接各点即可画出图形的另一半,使它成为一个轴对称图形。
【详解】
【点睛】掌握补全轴对称图形的步骤和方法是解题的关键。
25.【分析】①求种水稻的面积占总面积的几分之几,用种水稻的面积÷总面积即可;
②求种棉花的面积占总面积的几分之几,用种棉花的面积÷总面积即可;
③求种棉花的面积占水稻的面积的几分之几,用种棉花的面积÷水稻的面积即可。
【详解】①30÷50=
答:种水稻的面积占总面积的。
②(50-30)÷50
=20÷50
=
答:种棉花的面积占总面积的。
③(50-30)÷30
=20÷30
=
答:种棉花的面积占水稻的面积的。
【点睛】求一个数是(占)另一个数的几分之几,用除法。
26.86个
【分析】用13kg除以每个生日蛋糕的鲜牛奶的质量,求出可以做的蛋糕的数量,剩下的鲜牛奶不够做一个,用去尾法解决即可。
【详解】13÷0.15=86(个)……0.1(kg)≈86(个)
答:13kg鲜奶油最多可以做86个这种生日蛋糕。
【点睛】本题考查商的近似数,解答本题的关键是掌握用去尾法解决问题的计算方法。
27.见详解
【分析】根据能被2整除的数的特征和能被5整除的数的特征进行解答。
【详解】76个石榴,每5个装一袋,不能正好装完;每2个装一袋,能正好装完;因为76不是5的倍数,是2的倍数。
【点睛】此题考查的是能被2和5整除的数的特征的知识的应用。
28.1575平方厘米
【分析】可以把这个锦旗看作是一个长是60厘米,宽是30厘米的长方形面积减去下面的小三角形的面积,三角形的底是30厘米,高是:60-45=15(厘米),根据三角形的面积公式:底×高÷2,长方形的面积公式:长×宽,把数代入公式即可求解。
【详解】如图:
=1800-30×15÷2
=1800-225
(平方厘米)
答:制作一面锦旗至少需要1575平方厘米的布料。
【点睛】本题主要考查组合图形的面积的求法,可以把组合图形分成规则图形计算,同时熟练掌握规则图形的面积公式是解题的关键。
29.(1)6个球都是白球
(2)6个球都是黑球
(3)5个白球,1个黑球
(4)5个黑球,1个白球
【分析】(1)要使摸出的不可能是黑球,则盒子中没有黑球;
(2)要使摸出的一定是黑球,则盒子中只有6黑球;
(3)要使摸出白球的可能性大,则盒子中白球的数量最多,可放5个白球,1个黑球;
(4)要使摸出白球的可能性小,则盒子中白球的数量最少,可放5个黑球,1个白球。
【详解】(1)任意摸出一个球,不可能是黑球,即放入的6个球都是白球;
(2)任意摸出一个球,一定是黑球,放入的6个球都是黑球;
(3)摸多次,经常摸到白球,说明白球放得多,可以放5个白球,1个黑球;
(4)摸多次,偶尔摸到白球,说明放的白球少,可以放5个黑球,1个白球。
【点睛】本题考查了可能性,袋子中哪种颜色的球多,摸出的可能性就大。
30.1052名
【分析】士兵30人、50人或70人一排,结果都多出2名,则此时士兵的数量比30、50和70的公倍数多2。根据题意,韩信带领1500名将士与楚王大将李锋交战,汉军死伤四五百人,则剩下的士兵大约是1000名。先求出30、50和70的公倍数,再从中找出接近1000的数,最后加上2,就是韩信此时有士兵的数量。
用质因数分解法求几个数的最小公倍数,全部公有的质因数和各自独立的质因数,它们连乘的积就是这几个数的最小公倍数。再用最小公倍数分别乘2、3、4…,即可求出其他的公倍数。
【详解】30=3×2×5
50=5×2×5
70=7×2×5
30、50和70的最小公倍数是2×5×3×5×7=1050。
1050+2=1052(名)
答:韩信此时有1052名士兵。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
