第26章 反比例函数 章末综合练 2024--2025学年初中数学人教版九年级下册
文档属性
| 名称 | 第26章 反比例函数 章末综合练 2024--2025学年初中数学人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 706.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-03 17:35:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
反比例函数 章末综合练 2024--2025
学年初中数学人教版九年级下册
一、单选题
1.下列关系中,是反比例函数的是( )
A. B. C. D.
2.下列四个点中,在反比例函数y=的图象上的是( )
A.(﹣3,﹣2) B.(3,2) C.(﹣2,3) D.(﹣2,﹣3)
3.反比例函数经过点(2,1),则下列说法错误的是( )
A.点(﹣1,﹣2)在函数图象上
B.函数图象分布在第一、三象限
C.y随x的增大而减小
D.当y≥4时,0<x≤
4.如图所示,四边形ABCD的顶点都在坐标轴上,若AD∥BC,ACD与BCD的面积分别为20和40,若双曲线y=(k<0,x<0)恰好经过边AB的四等分点E(BE<AE),则k的值为( )
A.﹣5 B.﹣10 C.﹣15 D.﹣20
5.已知反比例函数,如果在这个函数图象所在的每一个象限内,y的值都随x的增大而增大,那么k的取值可能是( )
A.0 B.2 C.3 D.4
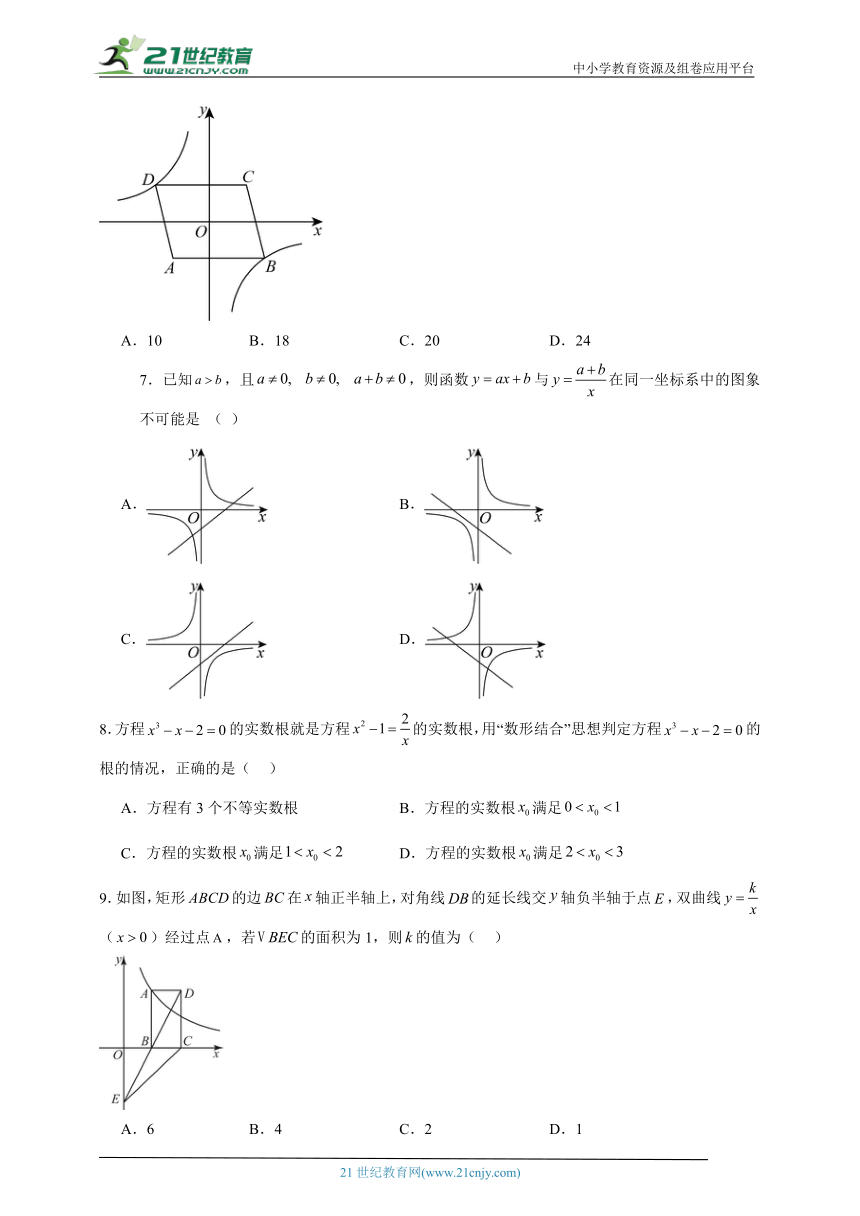
6.如图,在平面直角坐标系中,O为□ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB//x轴,反比例函数y=的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
A.10 B.18 C.20 D.24
7.已知,且,则函数与在同一坐标系中的图象不可能是 ( )
A. B.
C. D.
8.方程的实数根就是方程的实数根,用“数形结合”思想判定方程的根的情况,正确的是( )
A.方程有3个不等实数根 B.方程的实数根满足
C.方程的实数根满足 D.方程的实数根满足
9.如图,矩形的边在轴正半轴上,对角线的延长线交轴负半轴于点,双曲线()经过点,若的面积为1,则的值为( )
A.6 B.4 C.2 D.1
10.如图,正方形的顶点P,Q分别在反比例函数和的图象上,点M,N在x轴上,交y轴于点G,连接交y轴于点H,若,则( )
A. B. C. D.2
二、填空题
11.已知反比例函数 y=的图像都过A(1,3)则m= .
12.若点在函数图象上,那么的值为 .
13.如图,已知反比例函数和,点是上任意一点,连接交于点,分别过点、作轴、轴的平行线,得到矩形,则矩形的面积是 .
14.如图,A是反比例函数图象上的一点,AB垂直于x轴,垂足为B,AC垂直于y轴,垂足为C,若矩形ABOC的面积为5,则k的值为 .
15.如图,在平面直角坐标系中,函数y=(k>0)的图象经过点A(1,2)、B两点,过点A作x轴的垂线,垂足为C,连接AB、BC.若三角形ABC的面积为3,则点B的坐标为 .
三、解答题
16.已知与成正比例,与成反比例,当时,;当时,.
(1)求y与x的函数关系式;
(2)当时,求y的值.
17.已知一艘轮船上装有120吨货物,轮船到达目的地后开始卸货.设平均卸货速度为(单位:吨/小时),卸完这批货物所需的时间为(单位:小时).
(1)求关于的函数表达式;
(2)若要求不超过6小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
(3)按6小时卸完船上的这批货物,卸货2小时后,根据实际情况,要求剩下的货物要在2小时内卸完,在剩下的时间内每小时要多卸多少吨货物?
18.如图,一次函数 与反比例函数 的图象相交于,两点,连接,,延长交反比例函数图象于点C.
(1)求一次函数的表达式与反比例函数的表达式;
(2)当时,直接写出自变量x的取值范围为______;
(3)点P是x轴上一点,当时,请求出点P的坐标.
19.如图,菱形ABCD的顶点A、B分别在y轴与x轴正半轴上,C、D在第一象限,轴,反比例函数的图象经过顶点D.
(1)若,
①求反比例函数的解析式;
②证明:点C落在反比例函数的图象上;
(2)若,,求菱形ABCD的边长.
20.已知: 反比例函数经过点B(1,1) .
(1)求该反比例函数解析式;
(2)连接OB,再把点A(2,0)与点B连接,将△OAB绕点O按顺时针方向旋转135°得到△O,写出的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;
(3)若该反比例函数图象上有一点F(m,)(其中m>0),在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是,求代数式的值.
参考答案:
1.C
解:A和B均为正比例函数,D为平行于x轴的直线,只有C是反比例函数.
2.C
解:∵﹣3×(﹣2)=6,3×2=6,﹣2×3=﹣6,﹣2×(﹣3)=6,
∴点(﹣2,3)在反比例函数y=的图象上.
3.C
解:∵反比例函数经过点(2,1),
∴k=2.
∴﹣1×(﹣2)=2,故A正确;
∵k=2>0,
∴双曲线y=分布在第一、三象限,
故B选项正确;
∵当k=2>0时,反比例函数y=在每一个象限内y随x的增大而减小,故C选项错误,
当y≥4时,0<x≤,D选项正确,
综上,说法错误的是C,
4.A
解:∵AD∥BC,
∴.
∵△ACD与△BCD的面积分别为20和40,
∴△ABD和△BCD面积比为1:2,
∴根据同底得:AO:OC=DO:OB=1:2,
∴S△AOB=S△ABD=.
∵双曲线y=(k<0,x<0)恰好经过边AB的四等分点E(BE<AE),
∴,
∴,
∵双曲线经过第二象限,k<0,
∴k=﹣5.
5.A
解:∵反比例函数,如果在这个函数图象所在的每一个象限内,y的值都随x的增大而增大,
∴ ,
∴ ,所以k可能的取值只能是0.
6.C
∵AB=5,AB∥x轴交y轴于点E,点A的坐标为(-2,-2),
∴BE=5-2=3,OE=2,
∴B(3,-2)代入反比例函数的关系式得,k=-2×6=-6,
∴反比例函数的解析式为,
∵O为 ABCD的对称中心,点A的坐标为(-2,-2),
∴点C的坐标为(2,2),
平移后,如图,
当时,
∴点C′(2,-3),
∴CC′=2-(-3)=2+3=5,
CC′交AB于F,则AF=AE+EF=2+2=4,
∴平行四边形ACC′A′的面积为5×4=20,
7.B
A、由函数过一、三、四象限可知,>0,b<0;由函数的图象可知,>0,与已知>b,且≠0,b≠0,≠0,相吻合,故可能成立;
B、由函数过二、三、四象限可知,<0,b<0;由函数的图象可知,>0,两结论相矛盾,故不可能成立;
C、由函数过一、三、四象限可知,>0,b<0;由函数的图象可知,<0,与已知>b,且≠0,b≠0,≠0,相吻合,故可能成立;
D、由函数过一、三、四象限可知,<0,b<0;由函数的图象可知,<0,与已知>b,且≠0,b≠0,≠0,相吻合,故可能成立;故选B.
8.C
将方程的右边看作是反比例函数,左边看作是二次函数,
即反比例函数、二次函数在坐标系中的图像如下:
由图可知反比例函数、二次函数只有一个交点,且交点的横坐标在1和2之间,
则方程只有一个实数根,且实数根满足,
9.C
解:∵矩形的边在轴正半轴上,
∴轴,轴,,,
又∵,
∴,
即:.
又∵,
∴,
又∵反比例函数图象在第一象限,,
所以:.
10.B
解:∵正方形的顶点P,Q分别在反比例函数和的图象上,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴.
11.3.
解:把点A(1,3)代入函解析式得3=,解得m=3.
故答案为3.
12.
把点P(2,-3)代入函数数y=中可求出k的值.
由题意知,k=2×(-3)=-6,
故答案为-6.
13.
解:∵点A在上,
∴设A(a,),设直线OA的解析式为y=kx,
∴,则,即,
联立,解得:或(舍),
∴C(,),
∴在矩形ABCD中,
AB=CD=,AD=BC=,
∴矩形ABCD的面积为AB·AD==,
故答案为:.
14.5.
试题分析:由题意得:,则k=±5;又由于反比例函数图象位于一、三象限,k>0,则k=5,故答案为5.
考点:反比例函数系数k的几何意义.
15.(4,).
∵函数y=(x>0、常数k>0)的图象经过点A(1,2),
∴把(1,2)代入解析式得到2=,
∴k=2,
设B点的横坐标是m,
则AC边上的高是(m-1),
∵AC=2
∴根据三角形的面积公式得到×2 (m-1)=3,
∴m=4,把m=4代入y=,
∴B的纵坐标是,
∴点B的坐标是(4,).
故答案为(4,).
16.(1)
(2)5
(1)解:与成正比例,与成反比例,
设,,
,
,
把,代入得:,
解得:,
,
答:与的函数关系式是.
(2)解:当时,,
答:当时,的值是5.
17.(1)
(2)若货物不超过6小时卸完,则平均每小时至少要卸货20吨
(3)在剩下的时间内每小时要多卸20吨货物
(1)解:由题意可得:,则;
(2)解:把代入中,得:,
对于函数,当时,越小,越大.
这样若货物不超过6小时卸完,则平均每小时至少要卸货20吨.
(3)解:按6小时卸完船上的这批货物,卸货的速度为(吨/小时),
2小时后,货物还剩(吨),
则(吨/小时),
(吨),
在剩下的时间内每小时要多卸20吨货物.
18.(1),
(2)或
(3)或
(1)解:将,代入得 ,
解得 ,
∴一次函数为,
将代入 得,
解得,
∴反比例函数的解析式为 ;
(2)解:由图象可知,当时, 自变量x的取值范围为或,
故答案为:或;
(3)解:如图,由题意可知,,
∴,
把代入得,, 解得,
∴,
,
,
∴,
∴,即,
∴,
∴或,
19.(1)①;②见解析
(2)
(1)①解:过点D做y轴垂线交于点F,
∵为菱形,
∴,,
易证四边形AOBE、AEDF为矩形
∴,
∴,
∴
②证明:过点C做x轴垂线交于点G,
易证四边形AEBO、ACGO为矩形
∴,
∴,
∴C落在反比例函数的图象上;
(2)解:∵,,DB=2BE,AC=2AE,
∴设,则,,
∴BD=2BE=2,
∴
∵D在反比例函数上,
∴,
∴,
∴,
∴菱形ABCD的边长为6.
20.⑴;⑵点P在此双曲线上.⑶.
(1)设反比例函数关系式为y=(k≠0),
把(1,1)代入得:k=1,
∴反比例函数解析式:y=;
(2)∵已知B(1,1),A(2,0)
∴△OAB是等腰直角三角形
∵顺时针方向旋转135°,
∴B′(0,-),A′(-,-)
∴中点P为(-,-).
∵(-) (-)=1
∴点P在此双曲线上.
(3)∵EH=n,OM=m
∴S△OEM=OM EH=mn=,
∴m=
又∵F(m,m 1)在函数图象上
∴m(m 1)=1.
将m=代入上式,得
,
∴n2+n=
∴n2+n-2=-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
反比例函数 章末综合练 2024--2025
学年初中数学人教版九年级下册
一、单选题
1.下列关系中,是反比例函数的是( )
A. B. C. D.
2.下列四个点中,在反比例函数y=的图象上的是( )
A.(﹣3,﹣2) B.(3,2) C.(﹣2,3) D.(﹣2,﹣3)
3.反比例函数经过点(2,1),则下列说法错误的是( )
A.点(﹣1,﹣2)在函数图象上
B.函数图象分布在第一、三象限
C.y随x的增大而减小
D.当y≥4时,0<x≤
4.如图所示,四边形ABCD的顶点都在坐标轴上,若AD∥BC,ACD与BCD的面积分别为20和40,若双曲线y=(k<0,x<0)恰好经过边AB的四等分点E(BE<AE),则k的值为( )
A.﹣5 B.﹣10 C.﹣15 D.﹣20
5.已知反比例函数,如果在这个函数图象所在的每一个象限内,y的值都随x的增大而增大,那么k的取值可能是( )
A.0 B.2 C.3 D.4
6.如图,在平面直角坐标系中,O为□ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB//x轴,反比例函数y=的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
A.10 B.18 C.20 D.24
7.已知,且,则函数与在同一坐标系中的图象不可能是 ( )
A. B.
C. D.
8.方程的实数根就是方程的实数根,用“数形结合”思想判定方程的根的情况,正确的是( )
A.方程有3个不等实数根 B.方程的实数根满足
C.方程的实数根满足 D.方程的实数根满足
9.如图,矩形的边在轴正半轴上,对角线的延长线交轴负半轴于点,双曲线()经过点,若的面积为1,则的值为( )
A.6 B.4 C.2 D.1
10.如图,正方形的顶点P,Q分别在反比例函数和的图象上,点M,N在x轴上,交y轴于点G,连接交y轴于点H,若,则( )
A. B. C. D.2
二、填空题
11.已知反比例函数 y=的图像都过A(1,3)则m= .
12.若点在函数图象上,那么的值为 .
13.如图,已知反比例函数和,点是上任意一点,连接交于点,分别过点、作轴、轴的平行线,得到矩形,则矩形的面积是 .
14.如图,A是反比例函数图象上的一点,AB垂直于x轴,垂足为B,AC垂直于y轴,垂足为C,若矩形ABOC的面积为5,则k的值为 .
15.如图,在平面直角坐标系中,函数y=(k>0)的图象经过点A(1,2)、B两点,过点A作x轴的垂线,垂足为C,连接AB、BC.若三角形ABC的面积为3,则点B的坐标为 .
三、解答题
16.已知与成正比例,与成反比例,当时,;当时,.
(1)求y与x的函数关系式;
(2)当时,求y的值.
17.已知一艘轮船上装有120吨货物,轮船到达目的地后开始卸货.设平均卸货速度为(单位:吨/小时),卸完这批货物所需的时间为(单位:小时).
(1)求关于的函数表达式;
(2)若要求不超过6小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?
(3)按6小时卸完船上的这批货物,卸货2小时后,根据实际情况,要求剩下的货物要在2小时内卸完,在剩下的时间内每小时要多卸多少吨货物?
18.如图,一次函数 与反比例函数 的图象相交于,两点,连接,,延长交反比例函数图象于点C.
(1)求一次函数的表达式与反比例函数的表达式;
(2)当时,直接写出自变量x的取值范围为______;
(3)点P是x轴上一点,当时,请求出点P的坐标.
19.如图,菱形ABCD的顶点A、B分别在y轴与x轴正半轴上,C、D在第一象限,轴,反比例函数的图象经过顶点D.
(1)若,
①求反比例函数的解析式;
②证明:点C落在反比例函数的图象上;
(2)若,,求菱形ABCD的边长.
20.已知: 反比例函数经过点B(1,1) .
(1)求该反比例函数解析式;
(2)连接OB,再把点A(2,0)与点B连接,将△OAB绕点O按顺时针方向旋转135°得到△O,写出的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;
(3)若该反比例函数图象上有一点F(m,)(其中m>0),在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是,求代数式的值.
参考答案:
1.C
解:A和B均为正比例函数,D为平行于x轴的直线,只有C是反比例函数.
2.C
解:∵﹣3×(﹣2)=6,3×2=6,﹣2×3=﹣6,﹣2×(﹣3)=6,
∴点(﹣2,3)在反比例函数y=的图象上.
3.C
解:∵反比例函数经过点(2,1),
∴k=2.
∴﹣1×(﹣2)=2,故A正确;
∵k=2>0,
∴双曲线y=分布在第一、三象限,
故B选项正确;
∵当k=2>0时,反比例函数y=在每一个象限内y随x的增大而减小,故C选项错误,
当y≥4时,0<x≤,D选项正确,
综上,说法错误的是C,
4.A
解:∵AD∥BC,
∴.
∵△ACD与△BCD的面积分别为20和40,
∴△ABD和△BCD面积比为1:2,
∴根据同底得:AO:OC=DO:OB=1:2,
∴S△AOB=S△ABD=.
∵双曲线y=(k<0,x<0)恰好经过边AB的四等分点E(BE<AE),
∴,
∴,
∵双曲线经过第二象限,k<0,
∴k=﹣5.
5.A
解:∵反比例函数,如果在这个函数图象所在的每一个象限内,y的值都随x的增大而增大,
∴ ,
∴ ,所以k可能的取值只能是0.
6.C
∵AB=5,AB∥x轴交y轴于点E,点A的坐标为(-2,-2),
∴BE=5-2=3,OE=2,
∴B(3,-2)代入反比例函数的关系式得,k=-2×6=-6,
∴反比例函数的解析式为,
∵O为 ABCD的对称中心,点A的坐标为(-2,-2),
∴点C的坐标为(2,2),
平移后,如图,
当时,
∴点C′(2,-3),
∴CC′=2-(-3)=2+3=5,
CC′交AB于F,则AF=AE+EF=2+2=4,
∴平行四边形ACC′A′的面积为5×4=20,
7.B
A、由函数过一、三、四象限可知,>0,b<0;由函数的图象可知,>0,与已知>b,且≠0,b≠0,≠0,相吻合,故可能成立;
B、由函数过二、三、四象限可知,<0,b<0;由函数的图象可知,>0,两结论相矛盾,故不可能成立;
C、由函数过一、三、四象限可知,>0,b<0;由函数的图象可知,<0,与已知>b,且≠0,b≠0,≠0,相吻合,故可能成立;
D、由函数过一、三、四象限可知,<0,b<0;由函数的图象可知,<0,与已知>b,且≠0,b≠0,≠0,相吻合,故可能成立;故选B.
8.C
将方程的右边看作是反比例函数,左边看作是二次函数,
即反比例函数、二次函数在坐标系中的图像如下:
由图可知反比例函数、二次函数只有一个交点,且交点的横坐标在1和2之间,
则方程只有一个实数根,且实数根满足,
9.C
解:∵矩形的边在轴正半轴上,
∴轴,轴,,,
又∵,
∴,
即:.
又∵,
∴,
又∵反比例函数图象在第一象限,,
所以:.
10.B
解:∵正方形的顶点P,Q分别在反比例函数和的图象上,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴.
11.3.
解:把点A(1,3)代入函解析式得3=,解得m=3.
故答案为3.
12.
把点P(2,-3)代入函数数y=中可求出k的值.
由题意知,k=2×(-3)=-6,
故答案为-6.
13.
解:∵点A在上,
∴设A(a,),设直线OA的解析式为y=kx,
∴,则,即,
联立,解得:或(舍),
∴C(,),
∴在矩形ABCD中,
AB=CD=,AD=BC=,
∴矩形ABCD的面积为AB·AD==,
故答案为:.
14.5.
试题分析:由题意得:,则k=±5;又由于反比例函数图象位于一、三象限,k>0,则k=5,故答案为5.
考点:反比例函数系数k的几何意义.
15.(4,).
∵函数y=(x>0、常数k>0)的图象经过点A(1,2),
∴把(1,2)代入解析式得到2=,
∴k=2,
设B点的横坐标是m,
则AC边上的高是(m-1),
∵AC=2
∴根据三角形的面积公式得到×2 (m-1)=3,
∴m=4,把m=4代入y=,
∴B的纵坐标是,
∴点B的坐标是(4,).
故答案为(4,).
16.(1)
(2)5
(1)解:与成正比例,与成反比例,
设,,
,
,
把,代入得:,
解得:,
,
答:与的函数关系式是.
(2)解:当时,,
答:当时,的值是5.
17.(1)
(2)若货物不超过6小时卸完,则平均每小时至少要卸货20吨
(3)在剩下的时间内每小时要多卸20吨货物
(1)解:由题意可得:,则;
(2)解:把代入中,得:,
对于函数,当时,越小,越大.
这样若货物不超过6小时卸完,则平均每小时至少要卸货20吨.
(3)解:按6小时卸完船上的这批货物,卸货的速度为(吨/小时),
2小时后,货物还剩(吨),
则(吨/小时),
(吨),
在剩下的时间内每小时要多卸20吨货物.
18.(1),
(2)或
(3)或
(1)解:将,代入得 ,
解得 ,
∴一次函数为,
将代入 得,
解得,
∴反比例函数的解析式为 ;
(2)解:由图象可知,当时, 自变量x的取值范围为或,
故答案为:或;
(3)解:如图,由题意可知,,
∴,
把代入得,, 解得,
∴,
,
,
∴,
∴,即,
∴,
∴或,
19.(1)①;②见解析
(2)
(1)①解:过点D做y轴垂线交于点F,
∵为菱形,
∴,,
易证四边形AOBE、AEDF为矩形
∴,
∴,
∴
②证明:过点C做x轴垂线交于点G,
易证四边形AEBO、ACGO为矩形
∴,
∴,
∴C落在反比例函数的图象上;
(2)解:∵,,DB=2BE,AC=2AE,
∴设,则,,
∴BD=2BE=2,
∴
∵D在反比例函数上,
∴,
∴,
∴,
∴菱形ABCD的边长为6.
20.⑴;⑵点P在此双曲线上.⑶.
(1)设反比例函数关系式为y=(k≠0),
把(1,1)代入得:k=1,
∴反比例函数解析式:y=;
(2)∵已知B(1,1),A(2,0)
∴△OAB是等腰直角三角形
∵顺时针方向旋转135°,
∴B′(0,-),A′(-,-)
∴中点P为(-,-).
∵(-) (-)=1
∴点P在此双曲线上.
(3)∵EH=n,OM=m
∴S△OEM=OM EH=mn=,
∴m=
又∵F(m,m 1)在函数图象上
∴m(m 1)=1.
将m=代入上式,得
,
∴n2+n=
∴n2+n-2=-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
