2025届高考物理二轮复习讲义:微专题7 电磁感应中的单杆模型(含解析)
文档属性
| 名称 | 2025届高考物理二轮复习讲义:微专题7 电磁感应中的单杆模型(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 194.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-03 00:00:00 | ||
图片预览



文档简介
2025届高考物理二轮复习讲义:微专题7 电磁感应中的单杆模型
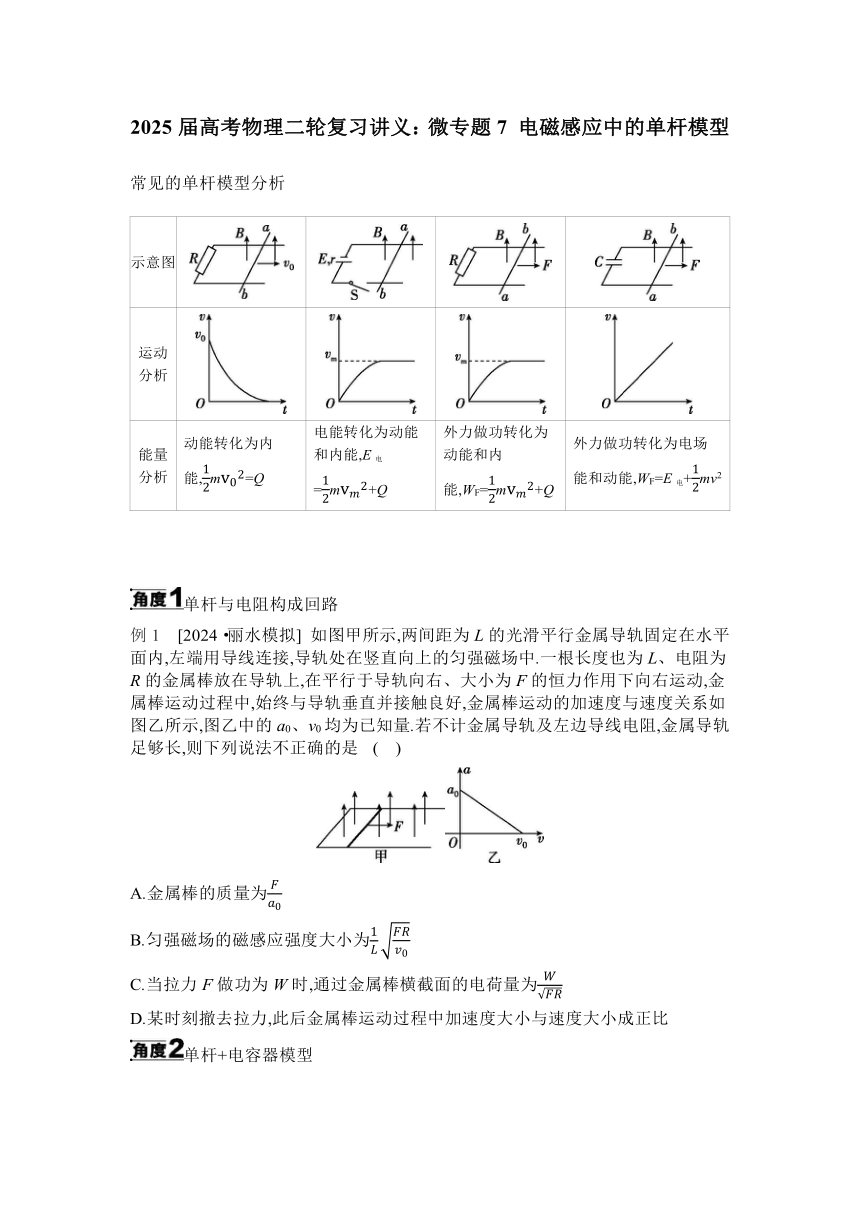
常见的单杆模型分析
示意图
运动 分析
能量 分析 动能转化为内能,m=Q 电能转化为动能和内能,E电=m+Q 外力做功转化为动能和内能,WF=m+Q 外力做功转化为电场能和动能,WF=E电+mv2
单杆与电阻构成回路
例1 [2024·丽水模拟] 如图甲所示,两间距为L的光滑平行金属导轨固定在水平面内,左端用导线连接,导轨处在竖直向上的匀强磁场中.一根长度也为L、电阻为R的金属棒放在导轨上,在平行于导轨向右、大小为F的恒力作用下向右运动,金属棒运动过程中,始终与导轨垂直并接触良好,金属棒运动的加速度与速度关系如图乙所示,图乙中的a0、v0均为已知量.若不计金属导轨及左边导线电阻,金属导轨足够长,则下列说法不正确的是 ( )
A.金属棒的质量为
B.匀强磁场的磁感应强度大小为
C.当拉力F做功为W时,通过金属棒横截面的电荷量为
D.某时刻撤去拉力,此后金属棒运动过程中加速度大小与速度大小成正比
单杆+电容器模型
例2 如图所示,光滑平行金属导轨弯折成对称的“V”字形,导轨间距为L,倾角为θ(很小)的倾斜部分与底部平滑连接,导轨位于方向竖直向上的匀强磁场中,磁感应强度大小为B(未知);在导轨左侧通过单刀双掷开关S可分别与电动势为E的电源(内阻为r)和极板为M和N的不带电的电容为C的电容器连接.将开关掷向1,长为L、质量为m的导体棒ab恰好能静止在倾斜导轨上高为h处.已知电容器始终工作在额定电压范围内,导体棒ab在运动过程中始终与导轨垂直且接触良好,重力加速度为g,不计其他电阻和电磁辐射.
(1)求磁感应强度B的大小;
(2)若将S掷向2,分析棒的运动情况.
单杆的振动(简谐运动)
例3 如图所示,PQ、MN是两条固定在水平面内的间距l=1 m的平行轨道,两轨道在O、O'处各有一小段长度可以忽略的绝缘体,绝缘体两侧为金属导轨,金属导轨电阻不计.轨道左端连接一个R=0.3 Ω的电阻,轨道右端连接一个“恒流源”,使导体棒ab在O、O'右侧时电流恒为I=0.5 A.沿轨道MN建立x轴,O为坐标原点,在两轨道间存在垂直于轨道平面向下的有界磁场,x≥0区域磁感应强度大小B随坐标x的变化规律为B=0.4x(T);-1 m≤x<0区域为匀强磁场,磁感应强度大小B0=0.2 T.开始时,质量m=0.05 kg、长度l=1 m、电阻r=0.1 Ω的导体棒ab在外力作用下静止在x=1.5 m处,ab棒与导轨间的动摩擦因数μ=0.2.现撤去外力,发现ab棒沿轨道向左运动.重力加速度g取10 m/s2.
(1)求撤去外力瞬间ab棒中的电流方向和ab棒的加速度大小;
(2)求撤去外力后ab棒由静止运动到x=0处的速度大小;
(3)若ab棒最终停在x0=-0.36 m处,其运动的总时间为多少 (已知:质量为m的物体做简谐运动时,回复力与物体偏离平衡位置的位移满足F回=-kx',且振动周期T=2π)
【跟踪训练】
1.[2024·宁波模拟] 如图所示,在水平桌面上固定两间距为d、长度足够的平行金属导轨,导轨间存在方向垂直于桌面向上、磁感应强度大小为B的匀强磁场.一质量为m的导体棒搁置于导轨间,通过水平绝缘细绳跨过轻质定滑轮与质量为M的重物相连.在导轨左侧,通过开关S可分别与含电阻、电容器和电感线圈的支路连接.在各种情况下导体棒均从静止开始运动,且在运动过程中始终垂直于导轨且接触良好,不计其他电阻、空气阻力、摩擦阻力和电磁辐射,当电感线圈中通有电流I时,电感线圈存储的磁能为LI2,重力加速度为g.
(1)若S掷向1,串接电阻,阻值为R,求导体棒运动的加速度与速度的关系;
(2)若S掷向2,串接一不带电的电容器,电容为C,求导体棒的速度与时间的关系;
(3)若S掷向3,串接一阻值为R的电阻和电感为L的电感线圈相串联的电路,当重物M下降高度为h时,重物开始做匀速运动.
①求重物匀速运动的速度大小v0;
②重物从静止开始下降高度为2h的过程中,求回路产生的焦耳热Q.
2.[2024·金华模拟] 某发光二极管D的伏安特性曲线如图甲所示,在达到正向导通电压UD=2.5 V后它才能够发光.因其发光时的伏安特性曲线斜率极大,可近似认为它发光后两端电压保持UD=2.5 V不变;电压小于UD或加反向电压时,它均处于截止状态,通过的电流为0.如图乙所示,现将其连接在固定于水平面上的电阻不计的两条平行导轨之间,两导轨间距离为L=0.1 m,整个导轨处于方向竖直向下、磁感应强度大小为B=10 T的匀强磁场中.取一根长度也为L、质量为m=0.01 kg、电阻为R=200 Ω的匀质导体棒,将其垂直置于两导轨上面,与两导轨间的动摩擦因数为μ=0.125.现给该导体棒一个水平向右、大小为v0=12.5 m/s的初速度,后续过程中导体棒与两导轨始终保持良好接触,经过t=3.2 s后发光二极管熄灭,g取10 m/s2.试求:
(1)D刚熄灭时,导体棒的速度大小;
(2)初始时刻,回路中的电流大小和导体棒的加速度大小;
(3)导体棒运动的整个过程中的位移大小;
(4)导体棒运动的整个过程中其产生的焦耳热.
参考答案与详细解析
例1 C [解析] 由牛顿第二定律可知F-=ma,整理得a=-v,结合图像可知=a0,解得m=,故A正确;结合图像可知=a0,解得B==,故B正确;当拉力F做功为W时,金属棒运动的距离为s=,则通过金属棒截面的电荷量q=Δt=Δt==,故C错误;某时刻撤去拉力,此后有=ma,则a=v,故D正确.
例2 (1)tan θ (2)见解析
[解析] (1)将开关掷向1,导体棒ab恰好静止在倾斜导轨上,故安培力沿导轨方向的分力与重力沿导轨方向的分力平衡,有
BILcos θ=mgsin θ
根据闭合电路欧姆定律得E=Ir
联立解得B=tan θ
(2)将开关掷向2,电容器两端电压与导体棒产生的感应电动势大小相等.以导体棒为研究对象,在左侧导轨上,由牛顿第二定律有
mgsin θ-BILcos θ=ma
回路中的电流I=====CBLacos θ
联立解得a=
所以a为定值,即棒在左侧导轨上做匀加速直线运动.同理,在右侧导轨上,由牛顿第二定律有
-BILcos θ-mgsin θ=ma'
回路中的电流I'===CBLa'cos θ
联立解得a'=-
所以a'为定值,即棒在右侧导轨上做匀减速运动,其运动情况与在左侧导轨上时对称.
例3 (1)b到a 4 m/s2 (2) m/s (3) s
[解析] (1)撤去外力瞬间ab棒沿轨道向左运动,说明受到向左的安培力作用,根据左手定则可判断出电流的方向从b到a.
对棒ab,由牛顿第二定律可得B1Il-μmg=ma
其中B1=0.4×1.5 T
解得a=4 m/s2
(2)撤去外力后ab棒由静止运动到x=0处的过程,由动能定理得
W安-μmgx1=m
由于磁感应强度B=0.4x(T)与x成线性关系,则安培力F安=BIl也与x成线性关系,所以W安=x1
其中x1=1.5 m-0
联立解得v0= m/s
(3)在x≥0区域中,棒受到的合力为F合=-BIL+μmg=-0.2(x-0.5) N
由简谐运动的性质可知,ab棒在x=1.5 m到x=0之间区域以x=0.5 m处为平衡位置做简谐运动,k=0.2 N/m,周期为T=2π=π s
ab棒从x=1.5 m处运动到x=0.5 m处所需时间t1== s
设ab棒从x=0.5 m处运动到x=0处所需时间为t2,由于==sin ,故t2== s
设棒ab在OO'左侧匀强磁场中运动时间为t3,由动量定理得
-B0lt3-μmgt3=0-mv0
其=,==
联立解得t3= s
则全程总时间t总=t1+t2+t3= s
【跟踪训练】
1.(1)a=g-v
(2)v=t
(3)①
②2Mgh--L
[解析] (1)若S掷向1,串接电阻,则闭合回路产生电流.设经过时间t,导体棒的速度为v,由牛顿第二定律,对重物有Mg-FT=Ma
对导体棒有FT-FA=ma
其中FA=BId,I=,E=Bdv
联立解得a=g-v
(2)若S掷向2,串接一不带电的电容器,则电容器两端电压与导体棒产生的感应电动势大小始终相等.同(1),有Mg-FT=Ma
FT-FA=ma
其中FA=BId,I====CBd=CBda
联立解得a=,
所以a为定值
则v=at=t
(3)①若S掷向3,串联一电阻和一电感线圈,则重物匀速运动时,电路稳恒,电感不起作用,有a0=g-v0=0
解得v0=
②由能量守恒定律有
2Mgh=+L+Q
其中I0=,E0=Bdv0
联立解得Q=2Mgh-(M+m)-L
2.(1)2.5 m/s
(2)0.05 A,6.25 m/s2 (3)22.5 m (4)0.35 J
[解析] (1)D刚熄灭时,有BLv=UD
解得导体棒的速度大小为v=2.5 m/s
(2)初始时刻,导体棒产生的电动势为E0=BLv0
根据闭合电路欧姆定律可得
E0=UD+I0R
解得回路中的电流大小为I0=0.05 A
以导体棒为对象,根据牛顿第二定律可得
BI0L+μmg=ma0
解得导体棒的加速度大小为a0=6.25 m/s2
(3)在发光二极管发光过程中,以导体棒为对象,根据动量定理可得-μmgt-BiLt=mv-mv0
其中i==
则有
联立解得该过程导体棒的位移大小为x1=20 m
发光二极管熄灭后,根据动能定理可得-μmgx2=0-mv2
解得该过程中导体棒的位移大小为x2=2.5 m
所以导体棒运动的整个过程中的位移大小为x=x1+x2=22.5 m
(4)导体棒运动的整个过程中,因摩擦产生的热量为Qf=μmgx
发光二极管发光过程中,发光二极管消耗的电能为
根据能量守恒定律可知,导体棒运动的整段过程中,导体棒产生的焦耳热为Q焦=m-Qf-ED
联立解得Q焦=0.35 J
常见的单杆模型分析
示意图
运动 分析
能量 分析 动能转化为内能,m=Q 电能转化为动能和内能,E电=m+Q 外力做功转化为动能和内能,WF=m+Q 外力做功转化为电场能和动能,WF=E电+mv2
单杆与电阻构成回路
例1 [2024·丽水模拟] 如图甲所示,两间距为L的光滑平行金属导轨固定在水平面内,左端用导线连接,导轨处在竖直向上的匀强磁场中.一根长度也为L、电阻为R的金属棒放在导轨上,在平行于导轨向右、大小为F的恒力作用下向右运动,金属棒运动过程中,始终与导轨垂直并接触良好,金属棒运动的加速度与速度关系如图乙所示,图乙中的a0、v0均为已知量.若不计金属导轨及左边导线电阻,金属导轨足够长,则下列说法不正确的是 ( )
A.金属棒的质量为
B.匀强磁场的磁感应强度大小为
C.当拉力F做功为W时,通过金属棒横截面的电荷量为
D.某时刻撤去拉力,此后金属棒运动过程中加速度大小与速度大小成正比
单杆+电容器模型
例2 如图所示,光滑平行金属导轨弯折成对称的“V”字形,导轨间距为L,倾角为θ(很小)的倾斜部分与底部平滑连接,导轨位于方向竖直向上的匀强磁场中,磁感应强度大小为B(未知);在导轨左侧通过单刀双掷开关S可分别与电动势为E的电源(内阻为r)和极板为M和N的不带电的电容为C的电容器连接.将开关掷向1,长为L、质量为m的导体棒ab恰好能静止在倾斜导轨上高为h处.已知电容器始终工作在额定电压范围内,导体棒ab在运动过程中始终与导轨垂直且接触良好,重力加速度为g,不计其他电阻和电磁辐射.
(1)求磁感应强度B的大小;
(2)若将S掷向2,分析棒的运动情况.
单杆的振动(简谐运动)
例3 如图所示,PQ、MN是两条固定在水平面内的间距l=1 m的平行轨道,两轨道在O、O'处各有一小段长度可以忽略的绝缘体,绝缘体两侧为金属导轨,金属导轨电阻不计.轨道左端连接一个R=0.3 Ω的电阻,轨道右端连接一个“恒流源”,使导体棒ab在O、O'右侧时电流恒为I=0.5 A.沿轨道MN建立x轴,O为坐标原点,在两轨道间存在垂直于轨道平面向下的有界磁场,x≥0区域磁感应强度大小B随坐标x的变化规律为B=0.4x(T);-1 m≤x<0区域为匀强磁场,磁感应强度大小B0=0.2 T.开始时,质量m=0.05 kg、长度l=1 m、电阻r=0.1 Ω的导体棒ab在外力作用下静止在x=1.5 m处,ab棒与导轨间的动摩擦因数μ=0.2.现撤去外力,发现ab棒沿轨道向左运动.重力加速度g取10 m/s2.
(1)求撤去外力瞬间ab棒中的电流方向和ab棒的加速度大小;
(2)求撤去外力后ab棒由静止运动到x=0处的速度大小;
(3)若ab棒最终停在x0=-0.36 m处,其运动的总时间为多少 (已知:质量为m的物体做简谐运动时,回复力与物体偏离平衡位置的位移满足F回=-kx',且振动周期T=2π)
【跟踪训练】
1.[2024·宁波模拟] 如图所示,在水平桌面上固定两间距为d、长度足够的平行金属导轨,导轨间存在方向垂直于桌面向上、磁感应强度大小为B的匀强磁场.一质量为m的导体棒搁置于导轨间,通过水平绝缘细绳跨过轻质定滑轮与质量为M的重物相连.在导轨左侧,通过开关S可分别与含电阻、电容器和电感线圈的支路连接.在各种情况下导体棒均从静止开始运动,且在运动过程中始终垂直于导轨且接触良好,不计其他电阻、空气阻力、摩擦阻力和电磁辐射,当电感线圈中通有电流I时,电感线圈存储的磁能为LI2,重力加速度为g.
(1)若S掷向1,串接电阻,阻值为R,求导体棒运动的加速度与速度的关系;
(2)若S掷向2,串接一不带电的电容器,电容为C,求导体棒的速度与时间的关系;
(3)若S掷向3,串接一阻值为R的电阻和电感为L的电感线圈相串联的电路,当重物M下降高度为h时,重物开始做匀速运动.
①求重物匀速运动的速度大小v0;
②重物从静止开始下降高度为2h的过程中,求回路产生的焦耳热Q.
2.[2024·金华模拟] 某发光二极管D的伏安特性曲线如图甲所示,在达到正向导通电压UD=2.5 V后它才能够发光.因其发光时的伏安特性曲线斜率极大,可近似认为它发光后两端电压保持UD=2.5 V不变;电压小于UD或加反向电压时,它均处于截止状态,通过的电流为0.如图乙所示,现将其连接在固定于水平面上的电阻不计的两条平行导轨之间,两导轨间距离为L=0.1 m,整个导轨处于方向竖直向下、磁感应强度大小为B=10 T的匀强磁场中.取一根长度也为L、质量为m=0.01 kg、电阻为R=200 Ω的匀质导体棒,将其垂直置于两导轨上面,与两导轨间的动摩擦因数为μ=0.125.现给该导体棒一个水平向右、大小为v0=12.5 m/s的初速度,后续过程中导体棒与两导轨始终保持良好接触,经过t=3.2 s后发光二极管熄灭,g取10 m/s2.试求:
(1)D刚熄灭时,导体棒的速度大小;
(2)初始时刻,回路中的电流大小和导体棒的加速度大小;
(3)导体棒运动的整个过程中的位移大小;
(4)导体棒运动的整个过程中其产生的焦耳热.
参考答案与详细解析
例1 C [解析] 由牛顿第二定律可知F-=ma,整理得a=-v,结合图像可知=a0,解得m=,故A正确;结合图像可知=a0,解得B==,故B正确;当拉力F做功为W时,金属棒运动的距离为s=,则通过金属棒截面的电荷量q=Δt=Δt==,故C错误;某时刻撤去拉力,此后有=ma,则a=v,故D正确.
例2 (1)tan θ (2)见解析
[解析] (1)将开关掷向1,导体棒ab恰好静止在倾斜导轨上,故安培力沿导轨方向的分力与重力沿导轨方向的分力平衡,有
BILcos θ=mgsin θ
根据闭合电路欧姆定律得E=Ir
联立解得B=tan θ
(2)将开关掷向2,电容器两端电压与导体棒产生的感应电动势大小相等.以导体棒为研究对象,在左侧导轨上,由牛顿第二定律有
mgsin θ-BILcos θ=ma
回路中的电流I=====CBLacos θ
联立解得a=
所以a为定值,即棒在左侧导轨上做匀加速直线运动.同理,在右侧导轨上,由牛顿第二定律有
-BILcos θ-mgsin θ=ma'
回路中的电流I'===CBLa'cos θ
联立解得a'=-
所以a'为定值,即棒在右侧导轨上做匀减速运动,其运动情况与在左侧导轨上时对称.
例3 (1)b到a 4 m/s2 (2) m/s (3) s
[解析] (1)撤去外力瞬间ab棒沿轨道向左运动,说明受到向左的安培力作用,根据左手定则可判断出电流的方向从b到a.
对棒ab,由牛顿第二定律可得B1Il-μmg=ma
其中B1=0.4×1.5 T
解得a=4 m/s2
(2)撤去外力后ab棒由静止运动到x=0处的过程,由动能定理得
W安-μmgx1=m
由于磁感应强度B=0.4x(T)与x成线性关系,则安培力F安=BIl也与x成线性关系,所以W安=x1
其中x1=1.5 m-0
联立解得v0= m/s
(3)在x≥0区域中,棒受到的合力为F合=-BIL+μmg=-0.2(x-0.5) N
由简谐运动的性质可知,ab棒在x=1.5 m到x=0之间区域以x=0.5 m处为平衡位置做简谐运动,k=0.2 N/m,周期为T=2π=π s
ab棒从x=1.5 m处运动到x=0.5 m处所需时间t1== s
设ab棒从x=0.5 m处运动到x=0处所需时间为t2,由于==sin ,故t2== s
设棒ab在OO'左侧匀强磁场中运动时间为t3,由动量定理得
-B0lt3-μmgt3=0-mv0
其=,==
联立解得t3= s
则全程总时间t总=t1+t2+t3= s
【跟踪训练】
1.(1)a=g-v
(2)v=t
(3)①
②2Mgh--L
[解析] (1)若S掷向1,串接电阻,则闭合回路产生电流.设经过时间t,导体棒的速度为v,由牛顿第二定律,对重物有Mg-FT=Ma
对导体棒有FT-FA=ma
其中FA=BId,I=,E=Bdv
联立解得a=g-v
(2)若S掷向2,串接一不带电的电容器,则电容器两端电压与导体棒产生的感应电动势大小始终相等.同(1),有Mg-FT=Ma
FT-FA=ma
其中FA=BId,I====CBd=CBda
联立解得a=,
所以a为定值
则v=at=t
(3)①若S掷向3,串联一电阻和一电感线圈,则重物匀速运动时,电路稳恒,电感不起作用,有a0=g-v0=0
解得v0=
②由能量守恒定律有
2Mgh=+L+Q
其中I0=,E0=Bdv0
联立解得Q=2Mgh-(M+m)-L
2.(1)2.5 m/s
(2)0.05 A,6.25 m/s2 (3)22.5 m (4)0.35 J
[解析] (1)D刚熄灭时,有BLv=UD
解得导体棒的速度大小为v=2.5 m/s
(2)初始时刻,导体棒产生的电动势为E0=BLv0
根据闭合电路欧姆定律可得
E0=UD+I0R
解得回路中的电流大小为I0=0.05 A
以导体棒为对象,根据牛顿第二定律可得
BI0L+μmg=ma0
解得导体棒的加速度大小为a0=6.25 m/s2
(3)在发光二极管发光过程中,以导体棒为对象,根据动量定理可得-μmgt-BiLt=mv-mv0
其中i==
则有
联立解得该过程导体棒的位移大小为x1=20 m
发光二极管熄灭后,根据动能定理可得-μmgx2=0-mv2
解得该过程中导体棒的位移大小为x2=2.5 m
所以导体棒运动的整个过程中的位移大小为x=x1+x2=22.5 m
(4)导体棒运动的整个过程中,因摩擦产生的热量为Qf=μmgx
发光二极管发光过程中,发光二极管消耗的电能为
根据能量守恒定律可知,导体棒运动的整段过程中,导体棒产生的焦耳热为Q焦=m-Qf-ED
联立解得Q焦=0.35 J
同课章节目录
