2025届高考物理二轮复习讲义:微专题9 电磁感应实践性应用专题 (含解析)
文档属性
| 名称 | 2025届高考物理二轮复习讲义:微专题9 电磁感应实践性应用专题 (含解析) | 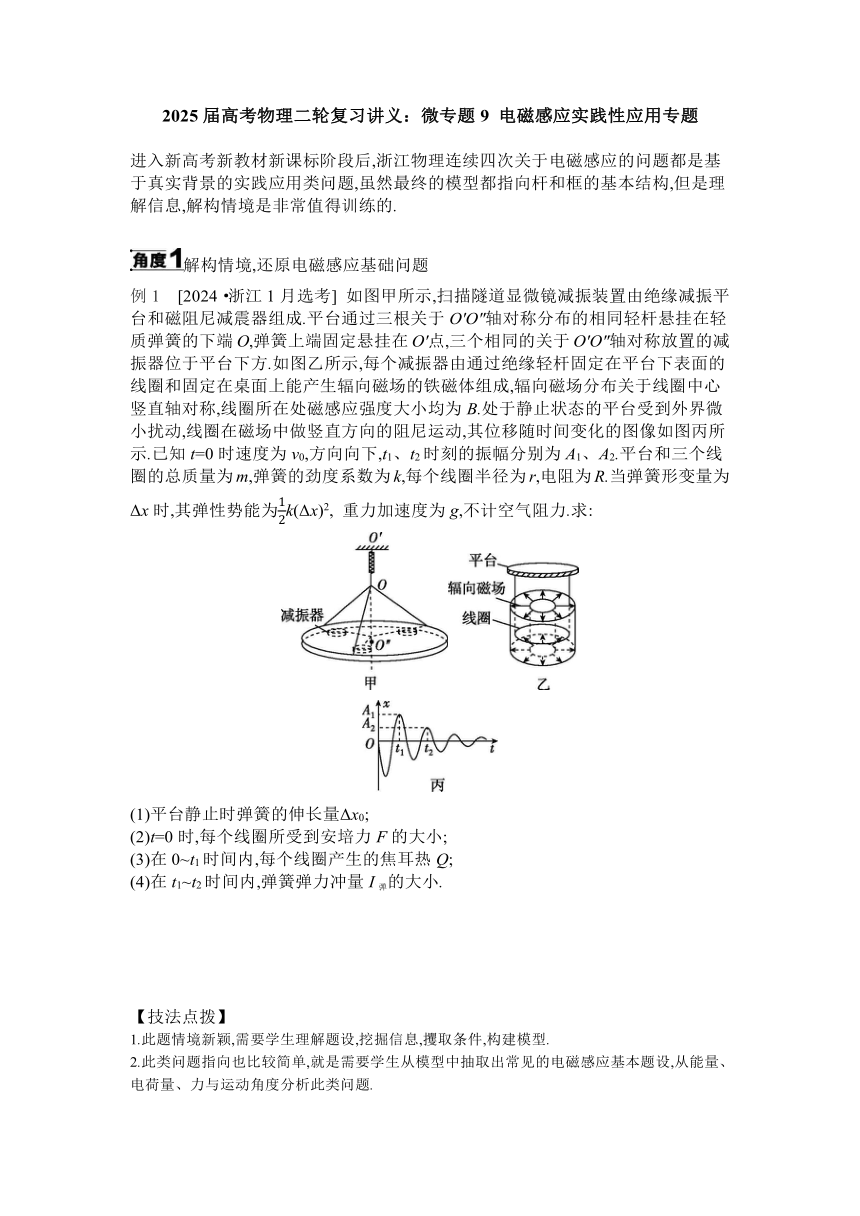 | |
| 格式 | docx | ||
| 文件大小 | 173.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-03 21:13:50 | ||
图片预览



文档简介
2025届高考物理二轮复习讲义:微专题9 电磁感应实践性应用专题
进入新高考新教材新课标阶段后,浙江物理连续四次关于电磁感应的问题都是基于真实背景的实践应用类问题,虽然最终的模型都指向杆和框的基本结构,但是理解信息,解构情境是非常值得训练的.
解构情境,还原电磁感应基础问题
例1 [2024·浙江1月选考] 如图甲所示,扫描隧道显微镜减振装置由绝缘减振平台和磁阻尼减震器组成.平台通过三根关于O'O″轴对称分布的相同轻杆悬挂在轻质弹簧的下端O,弹簧上端固定悬挂在O'点,三个相同的关于O'O″轴对称放置的减振器位于平台下方.如图乙所示,每个减振器由通过绝缘轻杆固定在平台下表面的线圈和固定在桌面上能产生辐向磁场的铁磁体组成,辐向磁场分布关于线圈中心竖直轴对称,线圈所在处磁感应强度大小均为B.处于静止状态的平台受到外界微小扰动,线圈在磁场中做竖直方向的阻尼运动,其位移随时间变化的图像如图丙所示.已知t=0时速度为v0,方向向下,t1、t2时刻的振幅分别为A1、A2.平台和三个线圈的总质量为m,弹簧的劲度系数为k,每个线圈半径为r,电阻为R.当弹簧形变量为Δx时,其弹性势能为k(Δx)2, 重力加速度为g,不计空气阻力.求:
(1)平台静止时弹簧的伸长量Δx0;
(2)t=0时,每个线圈所受到安培力F的大小;
(3)在0~t1时间内,每个线圈产生的焦耳热Q;
(4)在t1~t2时间内,弹簧弹力冲量I弹的大小.
【技法点拨】
1.此题情境新颖,需要学生理解题设,挖掘信息,攫取条件,构建模型.
2.此类问题指向也比较简单,就是需要学生从模型中抽取出常见的电磁感应基本题设,从能量、电荷量、力与运动角度分析此类问题.
利用题设信息运用创造性思维解决问题
例2 如图所示是简化的某种旋转磁极式发电机原理图.转子是中心在O点的条形磁铁,条形磁铁的长为2a,质量为m,横截面积为S,磁体两极的磁感应强度大小为B1;定子看成匝数n不同的两小线圈A、B,匝数n1>n2,二者轴线在同一平面内且相互垂直,两线圈到其轴线交点O的距离相等,且均连接阻值为R的电阻,线圈的长度远小于a,截面积小于S.线圈B通过单刀双掷开关K与两粗糙平行金属导轨相连,金属导轨所在平面与水平面的夹角为θ,处于垂直于导轨平面的匀强磁场中,磁感应强度的大小为B2,导轨间距为L,质量为M、电阻为r的金属棒PQ放置在导轨上,金属棒与导轨间的摩擦因数为μ(μ>tan θ).现用外力让条形磁铁绕O点在该平面内做角速度为ω的匀速圆周运动,两线圈输出正弦式交变电流.已知图示位置穿过线圈A的磁通量为穿过条形磁铁N极磁通量的k倍(k<1),条形磁铁以角速度ω匀速转动时,其动能Ek=ma2ω2,不计线圈、金属导轨的电阻及自感,忽略两线圈和磁场间的相互影响.
(1)以图示位置为t=0,写出A线圈中电流瞬时值的表达式;
(2)双掷开关K接1,条形磁铁匀速转动1圈,求A、B线圈所连电阻R产生的总焦耳热;
(3)双掷开关K接2,要使PQ始终静止在导轨上,求ω应满足的条件;
(4)双掷开关K接1,当撤去外力,条形磁铁将缓慢减速,经时间角速度减小量为Δω,求Δω的值.[当0【技法点拨】
1.此题和前述问题不一样在于题设情境更难把握,有些问题甚至从高视角俯瞰中学物理问题.
2.此类问题一般不会化简成固定范式,需要用一定创造力去解决,但计算复杂度和过程繁琐程度是远远小于一般问题的,难点在于是否能想到关键突破口.
【跟踪训练】
1.新能源汽车时代一项重要的技术是动能回收系统.其原理如图甲所示,当放开加速踏板时,汽车由于惯性会继续前行,此时回收系统会让机械组拖拽发电机线圈,切割磁感线产生感应电流,当逆变器输入电压高于UC时,电机可以为电池充电;当电压低于UC时,动能回收系统关闭.将质量为M的电动汽车的动能回收系统简化为如图乙所示的理想模型,间距为L的水平平行金属导轨处于竖直方向的磁感应强度为B的匀强磁场中,金属棒的质量等效为汽车的质量,金属棒在导轨上运动的速度等效为汽车速度,将动能回收系统的电阻等效为一外部电阻R.
(1)求逆变器输入电压等于UC时汽车的速度vC;
(2)求电动汽车以速度v(v>vC)开始制动时由动能回收系统产生的加速度的大小a;
(3)电动汽车以速度nvC(n>1)行驶时,突发情况采取紧急制动,动能回收系统开启时传统机械制动全程介入,传统机械制动阻力与车速成正比,即Ff=kv.速度降为vC时,动能回收系统关闭,传统机械制阻力变为车重的μ倍,重力加速度为g.若动能的回收率为η,求:
①制动过程中被回收的动能ΔEk;
②制动过程中电动汽车的总位移x.
2.[2024·宁波模拟] 现有一种利用电磁感应原理测血栓的传感器,该传感器部分的构成如图甲所示,激励线圈和反馈线圈分别装在两个圆盘上,两圆盘圆心在同一竖直线上.转盘a固定,其边缘围绕一组环形的激励线圈,内部铺装有许多点状磁感应强度传感器.转盘b可转动,内部单匝反馈线圈为“三叶式”,如图乙所示.该传感器工作原理:当检测部位放入两圆盘之间时,有血栓部位将导致反馈线圈所在圆盘对应区域磁感应强度发生变化,反馈线圈以角速度ω0转动时将产生感应电流,感应电流产生的磁场将导致磁传感器所在处的耦合磁场磁感应强度发生变化,从而确定血栓所在位置和大小.某次模拟测试时,放入半径为r2的扇形模拟血栓块,使得两圆盘之间对应区域磁感应强度为零.若反馈线圈处磁感应强度与激励线圈的电流关系为B=kI,反馈线圈单位长度的电阻为R,线圈内圈半径为r1=r,外圈半径r2=2r.[相关数学知识:sin =sin αcos β+cos αsin β,当Δθ≈0时,cos Δθ≈1,sin Δθ≈Δθ]
(1)若激励线圈接I=1 A的恒定电流,取k=0.1,ω0=30 rad/s,r= m,π≈3,R=0.1 Ω/m,求转动过程中反馈线圈所产生的感应电流大小;
(2)若反馈线圈不转动,模拟血栓块恰好与其中一叶片重叠,当激励线圈接i=Isin ωt的交流电时,求反馈线圈所产生的感应电动势;
(3)求(2)中单位时间内反馈线圈产生的热量.
参考答案与详细解析
例1 (1) (2)
(3)m- k
(4)mg(t2-t1)-(A1-A2)
[解析] (1)平台静止时,根据平衡条件有
kΔx0=mg
解得Δx0=
(2)t=0时,每个线圈切割磁感线产生的感应电动势E=BLv0
其中L=2πr
每个线圈中的电流I=
每个线圈所受安培力F=BIL
联立解得F=
(3)在0~t1时间内,弹簧的形变量Δx=-A1
根据能量守恒定律有
k(Δx0)2+ m=Q总+ k(Δx)2+mgA1
解得Q总=m- k
则Q=Q总=m- k
(4)在t1~t2时间内,根据动量定理有
I弹+I安-I重=0
其中,重力的冲量I重=mg(t2-t1)
安培力的冲量I安=3BLΔq
而Δq==
联立解得I弹=mg(t2-t1)-(A1-A2)
例2 (1)sin ωt
(2)
(3)ω≤
(4)
[解析] (1)A线圈产生的感应电动势的最大值Em=n1B1Sω·k
A线圈的电流随时间的表达式为i=sin ωt
(2)双掷开关K接1,条形磁铁匀速转1圈,两线圈产生的焦耳热分别为
QA=RT=·
QB=RT=·
所以总焦耳热
Q总=
(3)双掷开关K接2,电流从P流向Q时,有
FA1+Mgsin θ≤μMgcos θ
其中FA1=B2I1L=
解得ω1≤
电流从Q流向P时,有
FA2≤Mgsin θ+μMgcos θ
其中FA2=B2I2L=
解得ω2≤
所以要使PQ始终静止在导轨上,则角速度ω应满足
ω≤
(4)双掷开关K接1,撤去外力,条形磁铁将缓慢减速,动能转化为焦耳热,由于 1,所以经时间,条形磁铁转动近似1圈,有
Q总=ma2ω2-ma2(ω-Δω)2≈ω·Δω
联立解得Δω≈(+)
【跟踪训练】
1.(1) (2)
(3)①
②+
[解析] (1)逆变器输入电压等于UC时,有UC=BLvC
解得汽车速度vC=
(2)汽车速度为v时,感应电动势为E=BLv
电流为I=
安培力为F安=BIL
由动能回收系统产生的加速度的大小a=
联立解得a=
(3)①制动过程中被回收的动能ΔEk=×η=
②动能回收系统开启过程中,有(-F安-Ff)Δt=M(-Δv)
其中Ff=kv
联立可得Δt=MΔv
即x1=MvC(n-1)
解得x1=
动能回收系统关闭后,有
-μMgx2=0-M
解得x2=
制动过程中电动汽车的总位移x=x1+x2=+
2.(1)1 A (2)πr2kIωcos ωt (3)
[解析] (1)反馈线圈产生的感应电动势为E1=Bω0=kIω0(-)=0.5 V
反馈线圈的电阻为R1=R=0.5 Ω
则感应电流I1==1 A
(2)由题可知反馈线圈中有磁场覆盖的面积为S=π+π=πr2
由法拉第电磁感应定律可得
E=n===πr2k×
其中=I×=I×=I×=Iωcos ωt
故反馈线圈产生的感应电动势为Ea=πr2kIωcos ωt
(3)由(2)可知,励磁线圈在反馈线圈中产生的感应电动势为
Eb=πr2kIωcos ωt
其为交流电,有效值为E有效=
反馈线圈的电阻为Rb=πr2+πr1+6R=3rR
单位时间内反馈线圈产生的热量为Q=t
联立解得Q=
进入新高考新教材新课标阶段后,浙江物理连续四次关于电磁感应的问题都是基于真实背景的实践应用类问题,虽然最终的模型都指向杆和框的基本结构,但是理解信息,解构情境是非常值得训练的.
解构情境,还原电磁感应基础问题
例1 [2024·浙江1月选考] 如图甲所示,扫描隧道显微镜减振装置由绝缘减振平台和磁阻尼减震器组成.平台通过三根关于O'O″轴对称分布的相同轻杆悬挂在轻质弹簧的下端O,弹簧上端固定悬挂在O'点,三个相同的关于O'O″轴对称放置的减振器位于平台下方.如图乙所示,每个减振器由通过绝缘轻杆固定在平台下表面的线圈和固定在桌面上能产生辐向磁场的铁磁体组成,辐向磁场分布关于线圈中心竖直轴对称,线圈所在处磁感应强度大小均为B.处于静止状态的平台受到外界微小扰动,线圈在磁场中做竖直方向的阻尼运动,其位移随时间变化的图像如图丙所示.已知t=0时速度为v0,方向向下,t1、t2时刻的振幅分别为A1、A2.平台和三个线圈的总质量为m,弹簧的劲度系数为k,每个线圈半径为r,电阻为R.当弹簧形变量为Δx时,其弹性势能为k(Δx)2, 重力加速度为g,不计空气阻力.求:
(1)平台静止时弹簧的伸长量Δx0;
(2)t=0时,每个线圈所受到安培力F的大小;
(3)在0~t1时间内,每个线圈产生的焦耳热Q;
(4)在t1~t2时间内,弹簧弹力冲量I弹的大小.
【技法点拨】
1.此题情境新颖,需要学生理解题设,挖掘信息,攫取条件,构建模型.
2.此类问题指向也比较简单,就是需要学生从模型中抽取出常见的电磁感应基本题设,从能量、电荷量、力与运动角度分析此类问题.
利用题设信息运用创造性思维解决问题
例2 如图所示是简化的某种旋转磁极式发电机原理图.转子是中心在O点的条形磁铁,条形磁铁的长为2a,质量为m,横截面积为S,磁体两极的磁感应强度大小为B1;定子看成匝数n不同的两小线圈A、B,匝数n1>n2,二者轴线在同一平面内且相互垂直,两线圈到其轴线交点O的距离相等,且均连接阻值为R的电阻,线圈的长度远小于a,截面积小于S.线圈B通过单刀双掷开关K与两粗糙平行金属导轨相连,金属导轨所在平面与水平面的夹角为θ,处于垂直于导轨平面的匀强磁场中,磁感应强度的大小为B2,导轨间距为L,质量为M、电阻为r的金属棒PQ放置在导轨上,金属棒与导轨间的摩擦因数为μ(μ>tan θ).现用外力让条形磁铁绕O点在该平面内做角速度为ω的匀速圆周运动,两线圈输出正弦式交变电流.已知图示位置穿过线圈A的磁通量为穿过条形磁铁N极磁通量的k倍(k<1),条形磁铁以角速度ω匀速转动时,其动能Ek=ma2ω2,不计线圈、金属导轨的电阻及自感,忽略两线圈和磁场间的相互影响.
(1)以图示位置为t=0,写出A线圈中电流瞬时值的表达式;
(2)双掷开关K接1,条形磁铁匀速转动1圈,求A、B线圈所连电阻R产生的总焦耳热;
(3)双掷开关K接2,要使PQ始终静止在导轨上,求ω应满足的条件;
(4)双掷开关K接1,当撤去外力,条形磁铁将缓慢减速,经时间角速度减小量为Δω,求Δω的值.[当0
1.此题和前述问题不一样在于题设情境更难把握,有些问题甚至从高视角俯瞰中学物理问题.
2.此类问题一般不会化简成固定范式,需要用一定创造力去解决,但计算复杂度和过程繁琐程度是远远小于一般问题的,难点在于是否能想到关键突破口.
【跟踪训练】
1.新能源汽车时代一项重要的技术是动能回收系统.其原理如图甲所示,当放开加速踏板时,汽车由于惯性会继续前行,此时回收系统会让机械组拖拽发电机线圈,切割磁感线产生感应电流,当逆变器输入电压高于UC时,电机可以为电池充电;当电压低于UC时,动能回收系统关闭.将质量为M的电动汽车的动能回收系统简化为如图乙所示的理想模型,间距为L的水平平行金属导轨处于竖直方向的磁感应强度为B的匀强磁场中,金属棒的质量等效为汽车的质量,金属棒在导轨上运动的速度等效为汽车速度,将动能回收系统的电阻等效为一外部电阻R.
(1)求逆变器输入电压等于UC时汽车的速度vC;
(2)求电动汽车以速度v(v>vC)开始制动时由动能回收系统产生的加速度的大小a;
(3)电动汽车以速度nvC(n>1)行驶时,突发情况采取紧急制动,动能回收系统开启时传统机械制动全程介入,传统机械制动阻力与车速成正比,即Ff=kv.速度降为vC时,动能回收系统关闭,传统机械制阻力变为车重的μ倍,重力加速度为g.若动能的回收率为η,求:
①制动过程中被回收的动能ΔEk;
②制动过程中电动汽车的总位移x.
2.[2024·宁波模拟] 现有一种利用电磁感应原理测血栓的传感器,该传感器部分的构成如图甲所示,激励线圈和反馈线圈分别装在两个圆盘上,两圆盘圆心在同一竖直线上.转盘a固定,其边缘围绕一组环形的激励线圈,内部铺装有许多点状磁感应强度传感器.转盘b可转动,内部单匝反馈线圈为“三叶式”,如图乙所示.该传感器工作原理:当检测部位放入两圆盘之间时,有血栓部位将导致反馈线圈所在圆盘对应区域磁感应强度发生变化,反馈线圈以角速度ω0转动时将产生感应电流,感应电流产生的磁场将导致磁传感器所在处的耦合磁场磁感应强度发生变化,从而确定血栓所在位置和大小.某次模拟测试时,放入半径为r2的扇形模拟血栓块,使得两圆盘之间对应区域磁感应强度为零.若反馈线圈处磁感应强度与激励线圈的电流关系为B=kI,反馈线圈单位长度的电阻为R,线圈内圈半径为r1=r,外圈半径r2=2r.[相关数学知识:sin =sin αcos β+cos αsin β,当Δθ≈0时,cos Δθ≈1,sin Δθ≈Δθ]
(1)若激励线圈接I=1 A的恒定电流,取k=0.1,ω0=30 rad/s,r= m,π≈3,R=0.1 Ω/m,求转动过程中反馈线圈所产生的感应电流大小;
(2)若反馈线圈不转动,模拟血栓块恰好与其中一叶片重叠,当激励线圈接i=Isin ωt的交流电时,求反馈线圈所产生的感应电动势;
(3)求(2)中单位时间内反馈线圈产生的热量.
参考答案与详细解析
例1 (1) (2)
(3)m- k
(4)mg(t2-t1)-(A1-A2)
[解析] (1)平台静止时,根据平衡条件有
kΔx0=mg
解得Δx0=
(2)t=0时,每个线圈切割磁感线产生的感应电动势E=BLv0
其中L=2πr
每个线圈中的电流I=
每个线圈所受安培力F=BIL
联立解得F=
(3)在0~t1时间内,弹簧的形变量Δx=-A1
根据能量守恒定律有
k(Δx0)2+ m=Q总+ k(Δx)2+mgA1
解得Q总=m- k
则Q=Q总=m- k
(4)在t1~t2时间内,根据动量定理有
I弹+I安-I重=0
其中,重力的冲量I重=mg(t2-t1)
安培力的冲量I安=3BLΔq
而Δq==
联立解得I弹=mg(t2-t1)-(A1-A2)
例2 (1)sin ωt
(2)
(3)ω≤
(4)
[解析] (1)A线圈产生的感应电动势的最大值Em=n1B1Sω·k
A线圈的电流随时间的表达式为i=sin ωt
(2)双掷开关K接1,条形磁铁匀速转1圈,两线圈产生的焦耳热分别为
QA=RT=·
QB=RT=·
所以总焦耳热
Q总=
(3)双掷开关K接2,电流从P流向Q时,有
FA1+Mgsin θ≤μMgcos θ
其中FA1=B2I1L=
解得ω1≤
电流从Q流向P时,有
FA2≤Mgsin θ+μMgcos θ
其中FA2=B2I2L=
解得ω2≤
所以要使PQ始终静止在导轨上,则角速度ω应满足
ω≤
(4)双掷开关K接1,撤去外力,条形磁铁将缓慢减速,动能转化为焦耳热,由于 1,所以经时间,条形磁铁转动近似1圈,有
Q总=ma2ω2-ma2(ω-Δω)2≈ω·Δω
联立解得Δω≈(+)
【跟踪训练】
1.(1) (2)
(3)①
②+
[解析] (1)逆变器输入电压等于UC时,有UC=BLvC
解得汽车速度vC=
(2)汽车速度为v时,感应电动势为E=BLv
电流为I=
安培力为F安=BIL
由动能回收系统产生的加速度的大小a=
联立解得a=
(3)①制动过程中被回收的动能ΔEk=×η=
②动能回收系统开启过程中,有(-F安-Ff)Δt=M(-Δv)
其中Ff=kv
联立可得Δt=MΔv
即x1=MvC(n-1)
解得x1=
动能回收系统关闭后,有
-μMgx2=0-M
解得x2=
制动过程中电动汽车的总位移x=x1+x2=+
2.(1)1 A (2)πr2kIωcos ωt (3)
[解析] (1)反馈线圈产生的感应电动势为E1=Bω0=kIω0(-)=0.5 V
反馈线圈的电阻为R1=R=0.5 Ω
则感应电流I1==1 A
(2)由题可知反馈线圈中有磁场覆盖的面积为S=π+π=πr2
由法拉第电磁感应定律可得
E=n===πr2k×
其中=I×=I×=I×=Iωcos ωt
故反馈线圈产生的感应电动势为Ea=πr2kIωcos ωt
(3)由(2)可知,励磁线圈在反馈线圈中产生的感应电动势为
Eb=πr2kIωcos ωt
其为交流电,有效值为E有效=
反馈线圈的电阻为Rb=πr2+πr1+6R=3rR
单位时间内反馈线圈产生的热量为Q=t
联立解得Q=
同课章节目录
