人教版(2024)数学七年级下册 第七章 相交线与平行线 基础复习(含答案)
文档属性
| 名称 | 人教版(2024)数学七年级下册 第七章 相交线与平行线 基础复习(含答案) | 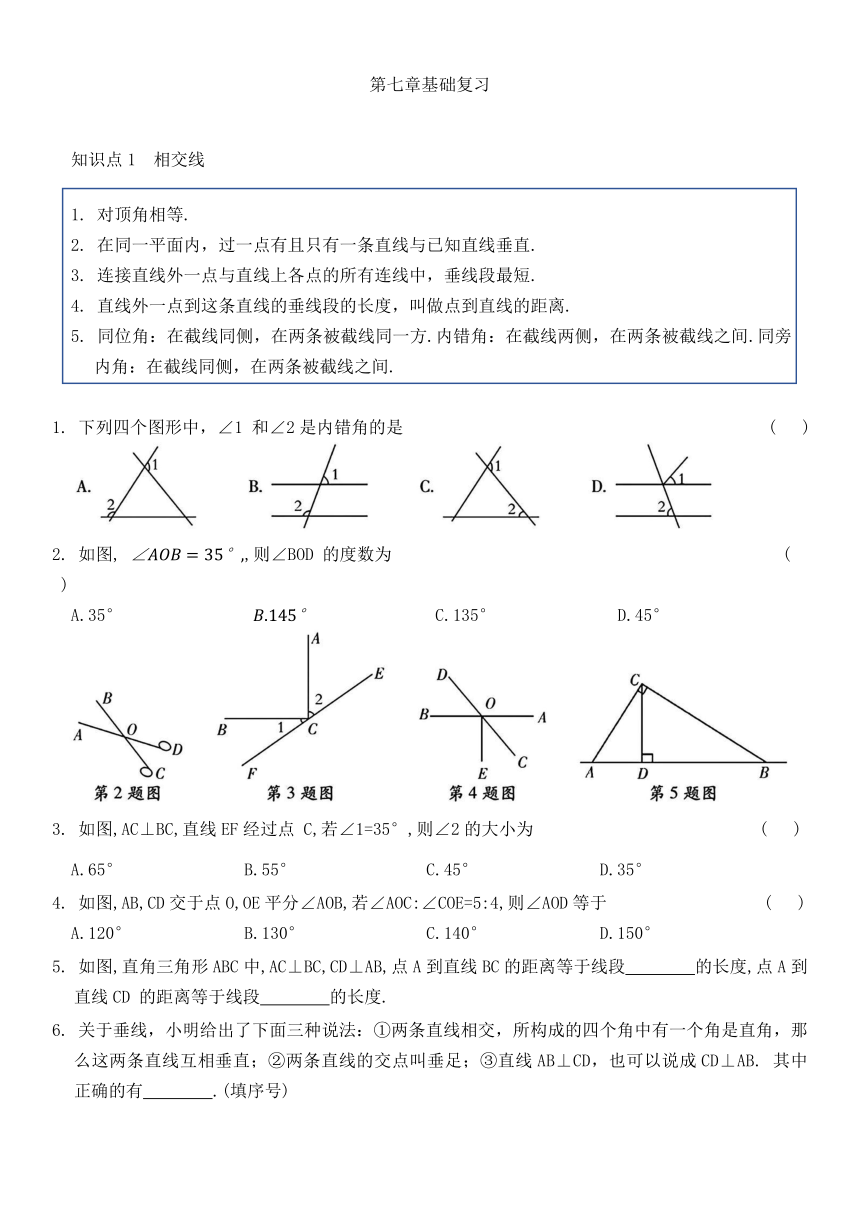 | |
| 格式 | docx | ||
| 文件大小 | 212.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 10:53:36 | ||
图片预览


文档简介
第七章基础复习
知识点1 相交线
1. 对顶角相等.
2. 在同一平面内,过一点有且只有一条直线与已知直线垂直.
3. 连接直线外一点与直线上各点的所有连线中,垂线段最短.
4. 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
5. 同位角:在截线同侧,在两条被截线同一方.内错角:在截线两侧,在两条被截线之间.同旁内角:在截线同侧,在两条被截线之间.
1. 下列四个图形中,∠1 和∠2是内错角的是 ( )
2. 如图, ,则∠BOD 的度数为 ( )
A.35° C.135° D.45°
3. 如图,AC⊥BC,直线EF经过点 C,若∠1=35°,则∠2的大小为 ( )
A.65° B.55° C.45° D.35°
4. 如图,AB,CD交于点O,OE平分∠AOB,若∠AOC:∠COE=5:4,则∠AOD等于 ( )
A.120° B.130° C.140° D.150°
5. 如图,直角三角形ABC中,AC⊥BC,CD⊥AB,点A到直线BC的距离等于线段 的长度,点A到直线CD 的距离等于线段 的长度.
6. 关于垂线,小明给出了下面三种说法:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直;②两条直线的交点叫垂足;③直线AB⊥CD,也可以说成CD⊥AB. 其中正确的有 .(填序号)
7. 如图所示,王师傅为了检验门框AB 是否垂直于地面,在门框AB 的上端A处用细线悬挂一铅锤,看门框AB 是否与铅锤线重合. 若门框AB 垂直于地面,则AB 会重合于AE,否则AB与AE不重合. 请你用所学的数学知识说明道理:
8. 如图,点O 是直线AB 上一点,射线OD 平分 若 求 的度数.
9. 如图,直线AB,CD相交于点O,OA平分.
的对顶角为 ,.∠AOC的邻补角为 .
(2)若 求 的度数.
(3)若 求 的度数.
知识点 2 平行线及其判定
1. 经过直线外一点,有且只有一条直线与这条直线平行.
2. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
3. 平行线的判定:①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行.
10. 下列语句正确的是 ( )
A. 60°角的余角是120°
B. 平面内,过直线外一点有且只有一条直线与已知直线平行
C. 不相交的两条直线叫平行线
D. 同旁内角互补
11. 木工师傅用图中的角尺画平行线,他依据的数学道理是 ( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 以上结论都不正确
12. 如图,下列推理中正确的是 ( )
A.∵∠1=∠4,∴BC∥AD B.∵∠2=∠3,∴AB∥CD
C.∵∠BCD+∠ADC=180°,∴AD∥BC D.∵∠CBA+∠C=180°,∴BC∥AD
13. 如图,直线a和b 被直线c所截,∠1 =110°,当 时,直线a∥b.
14. 如图,已知∠DAC=∠ACB,∠D+∠DFE=180°,那么EF与BC平行吗 为什么
知识点3平行线的性质
1. 平行线的性质:①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补.
2. 判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
15. 下列命题是真命题的是 ( )
A. 如果 那么a=b
B. 在同一平面内,平行于同一条直线的两直线平行
C. 两直线相交,其中相等的两个角是对顶角
D. 如果两个角是同位角,那么这两个角相等
16. 如图,AC∥BD,AE平分∠BAC交BD 于点E,若∠1=64°,则∠2= ( )
A.116° B.122° C.128° D.142°
17. 如图,如果∠1 =∠3,∠2=64°,那么∠4 的度数为 .
18. 如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
19. 完成下面的证明:
已知:如图,DE∥BC,BD平分∠ABC,EF平分∠AED. 求证:
证明:∵DE∥BC( ( ),∴∠ABC= ).
∵BD平分∠ABC,EF平分∠AED(已知),
∴∠1= ( ).
∴EF∥BD( ).
∴∠EFD +∠BDF=180°( ).
知识点4 平 移
把一个图形沿着一定的方向移动一定的距离,图形的这种移动,叫做平移,平移不改变图形的大小和形状.平移后,各组对应点的连线平行(或在同一条直线上)且相等.
20. 把三角形ABC沿BC方向平移,得到三角形 ,随着平移距离的不断增大,三角形 的面积大小变化情况是 ( )
A. 增大 B. 减小 C. 不变 D. 不确定
21. 如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE 的周长是10 cm,那么四边形ABFD 的周长是 ( )
A.12 cm B.16 cm C.18 cm D.20cm
22. 如图,三角形ABC沿AB 方向向右平移后到达三角形. 的位置,BC与 相交于点O,若∠C的度数为x,则∠A OC 的度数为 ( )
A. x B.90°-x
23. 如图,根据图中给出的数据判断两个图形的周长的关系: .(填“相等”或“不相等”或“无法判断”)
24. 如图,在三角形ABC中,BC=4 cm. 现将三角形ABC沿着垂直于 BC 的方向平移5cm 到达三角形 DEF的位置,则三角形ABC 的边AC,AB 所扫过的面积是 cm .
第七章基础复习
1. C 2. B 3. B 4. B 5. AC AD 6.①③
7. 在同一平面内,过一点有且只有一条直线与已知直线垂直
8. 解:因为OD平分∠AOC,所以∠AOD=∠DOC=30°.
又OD⊥OE,所以∠DOE=90°.
所以.
9. 解:(1)根据对顶角、邻补角的意义,得∠AOC 的对顶角为∠BOD;
∠AOC 的邻补角为∠BOC 或∠AOD. 故答案为:∠BOD;∠BOC或∠AOD.
(2)因为OA平分∠EOC,∠EOC=70°,所以∠AOE=∠AOC 又∠AOC=∠BOD,所以∠BOD=35°.
(3)因为∠EOC:∠EOD=2:3,∠EOC+∠EOD =180°,所以∠EOC = 72°,∠EOD = 108°. 因为 OA 平分∠EOC,所以 又∠AOC =∠BOD,所以∠BOD=36°.
10. B 11. A 12. C 13.70°
14. 解:EF∥BC,理由如下:∵∠DAC=∠ACB,∴AD∥BC.
∵∠D+∠DFE=180°,∴AD∥EF.∴EF∥BC.
15. B 16. B 17.116° 18.45°
19. 证明:∵DE∥BC(已知),
∴∠ABC=∠AED(两直线平行,同位角相等).
∵BD平分∠ABC,EF平分∠AED (已知),
( 角平分线的定义).
∴∠1=∠2(等量代换).
∴EF∥BD(同位角相等,两直线平行).
∴∠EFD+∠BDF=180°(两直线平行,同旁内角互补).
故答案为:已知;∠AED;两直线平行,同位角相等;∠ABC;∠AED;角平分线的定义;∠2;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
20. C 21. A 22. C 23. 不相等 24.20
知识点1 相交线
1. 对顶角相等.
2. 在同一平面内,过一点有且只有一条直线与已知直线垂直.
3. 连接直线外一点与直线上各点的所有连线中,垂线段最短.
4. 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
5. 同位角:在截线同侧,在两条被截线同一方.内错角:在截线两侧,在两条被截线之间.同旁内角:在截线同侧,在两条被截线之间.
1. 下列四个图形中,∠1 和∠2是内错角的是 ( )
2. 如图, ,则∠BOD 的度数为 ( )
A.35° C.135° D.45°
3. 如图,AC⊥BC,直线EF经过点 C,若∠1=35°,则∠2的大小为 ( )
A.65° B.55° C.45° D.35°
4. 如图,AB,CD交于点O,OE平分∠AOB,若∠AOC:∠COE=5:4,则∠AOD等于 ( )
A.120° B.130° C.140° D.150°
5. 如图,直角三角形ABC中,AC⊥BC,CD⊥AB,点A到直线BC的距离等于线段 的长度,点A到直线CD 的距离等于线段 的长度.
6. 关于垂线,小明给出了下面三种说法:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直;②两条直线的交点叫垂足;③直线AB⊥CD,也可以说成CD⊥AB. 其中正确的有 .(填序号)
7. 如图所示,王师傅为了检验门框AB 是否垂直于地面,在门框AB 的上端A处用细线悬挂一铅锤,看门框AB 是否与铅锤线重合. 若门框AB 垂直于地面,则AB 会重合于AE,否则AB与AE不重合. 请你用所学的数学知识说明道理:
8. 如图,点O 是直线AB 上一点,射线OD 平分 若 求 的度数.
9. 如图,直线AB,CD相交于点O,OA平分.
的对顶角为 ,.∠AOC的邻补角为 .
(2)若 求 的度数.
(3)若 求 的度数.
知识点 2 平行线及其判定
1. 经过直线外一点,有且只有一条直线与这条直线平行.
2. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
3. 平行线的判定:①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行.
10. 下列语句正确的是 ( )
A. 60°角的余角是120°
B. 平面内,过直线外一点有且只有一条直线与已知直线平行
C. 不相交的两条直线叫平行线
D. 同旁内角互补
11. 木工师傅用图中的角尺画平行线,他依据的数学道理是 ( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 以上结论都不正确
12. 如图,下列推理中正确的是 ( )
A.∵∠1=∠4,∴BC∥AD B.∵∠2=∠3,∴AB∥CD
C.∵∠BCD+∠ADC=180°,∴AD∥BC D.∵∠CBA+∠C=180°,∴BC∥AD
13. 如图,直线a和b 被直线c所截,∠1 =110°,当 时,直线a∥b.
14. 如图,已知∠DAC=∠ACB,∠D+∠DFE=180°,那么EF与BC平行吗 为什么
知识点3平行线的性质
1. 平行线的性质:①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补.
2. 判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
15. 下列命题是真命题的是 ( )
A. 如果 那么a=b
B. 在同一平面内,平行于同一条直线的两直线平行
C. 两直线相交,其中相等的两个角是对顶角
D. 如果两个角是同位角,那么这两个角相等
16. 如图,AC∥BD,AE平分∠BAC交BD 于点E,若∠1=64°,则∠2= ( )
A.116° B.122° C.128° D.142°
17. 如图,如果∠1 =∠3,∠2=64°,那么∠4 的度数为 .
18. 如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
19. 完成下面的证明:
已知:如图,DE∥BC,BD平分∠ABC,EF平分∠AED. 求证:
证明:∵DE∥BC( ( ),∴∠ABC= ).
∵BD平分∠ABC,EF平分∠AED(已知),
∴∠1= ( ).
∴EF∥BD( ).
∴∠EFD +∠BDF=180°( ).
知识点4 平 移
把一个图形沿着一定的方向移动一定的距离,图形的这种移动,叫做平移,平移不改变图形的大小和形状.平移后,各组对应点的连线平行(或在同一条直线上)且相等.
20. 把三角形ABC沿BC方向平移,得到三角形 ,随着平移距离的不断增大,三角形 的面积大小变化情况是 ( )
A. 增大 B. 减小 C. 不变 D. 不确定
21. 如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE 的周长是10 cm,那么四边形ABFD 的周长是 ( )
A.12 cm B.16 cm C.18 cm D.20cm
22. 如图,三角形ABC沿AB 方向向右平移后到达三角形. 的位置,BC与 相交于点O,若∠C的度数为x,则∠A OC 的度数为 ( )
A. x B.90°-x
23. 如图,根据图中给出的数据判断两个图形的周长的关系: .(填“相等”或“不相等”或“无法判断”)
24. 如图,在三角形ABC中,BC=4 cm. 现将三角形ABC沿着垂直于 BC 的方向平移5cm 到达三角形 DEF的位置,则三角形ABC 的边AC,AB 所扫过的面积是 cm .
第七章基础复习
1. C 2. B 3. B 4. B 5. AC AD 6.①③
7. 在同一平面内,过一点有且只有一条直线与已知直线垂直
8. 解:因为OD平分∠AOC,所以∠AOD=∠DOC=30°.
又OD⊥OE,所以∠DOE=90°.
所以.
9. 解:(1)根据对顶角、邻补角的意义,得∠AOC 的对顶角为∠BOD;
∠AOC 的邻补角为∠BOC 或∠AOD. 故答案为:∠BOD;∠BOC或∠AOD.
(2)因为OA平分∠EOC,∠EOC=70°,所以∠AOE=∠AOC 又∠AOC=∠BOD,所以∠BOD=35°.
(3)因为∠EOC:∠EOD=2:3,∠EOC+∠EOD =180°,所以∠EOC = 72°,∠EOD = 108°. 因为 OA 平分∠EOC,所以 又∠AOC =∠BOD,所以∠BOD=36°.
10. B 11. A 12. C 13.70°
14. 解:EF∥BC,理由如下:∵∠DAC=∠ACB,∴AD∥BC.
∵∠D+∠DFE=180°,∴AD∥EF.∴EF∥BC.
15. B 16. B 17.116° 18.45°
19. 证明:∵DE∥BC(已知),
∴∠ABC=∠AED(两直线平行,同位角相等).
∵BD平分∠ABC,EF平分∠AED (已知),
( 角平分线的定义).
∴∠1=∠2(等量代换).
∴EF∥BD(同位角相等,两直线平行).
∴∠EFD+∠BDF=180°(两直线平行,同旁内角互补).
故答案为:已知;∠AED;两直线平行,同位角相等;∠ABC;∠AED;角平分线的定义;∠2;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
20. C 21. A 22. C 23. 不相等 24.20
同课章节目录
