人教版(2024)数学七年级下册 第七章 相交线与平行线 综合测试卷(含答案)
文档属性
| 名称 | 人教版(2024)数学七年级下册 第七章 相交线与平行线 综合测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 240.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 10:54:19 | ||
图片预览

文档简介
第七章综合测试卷
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
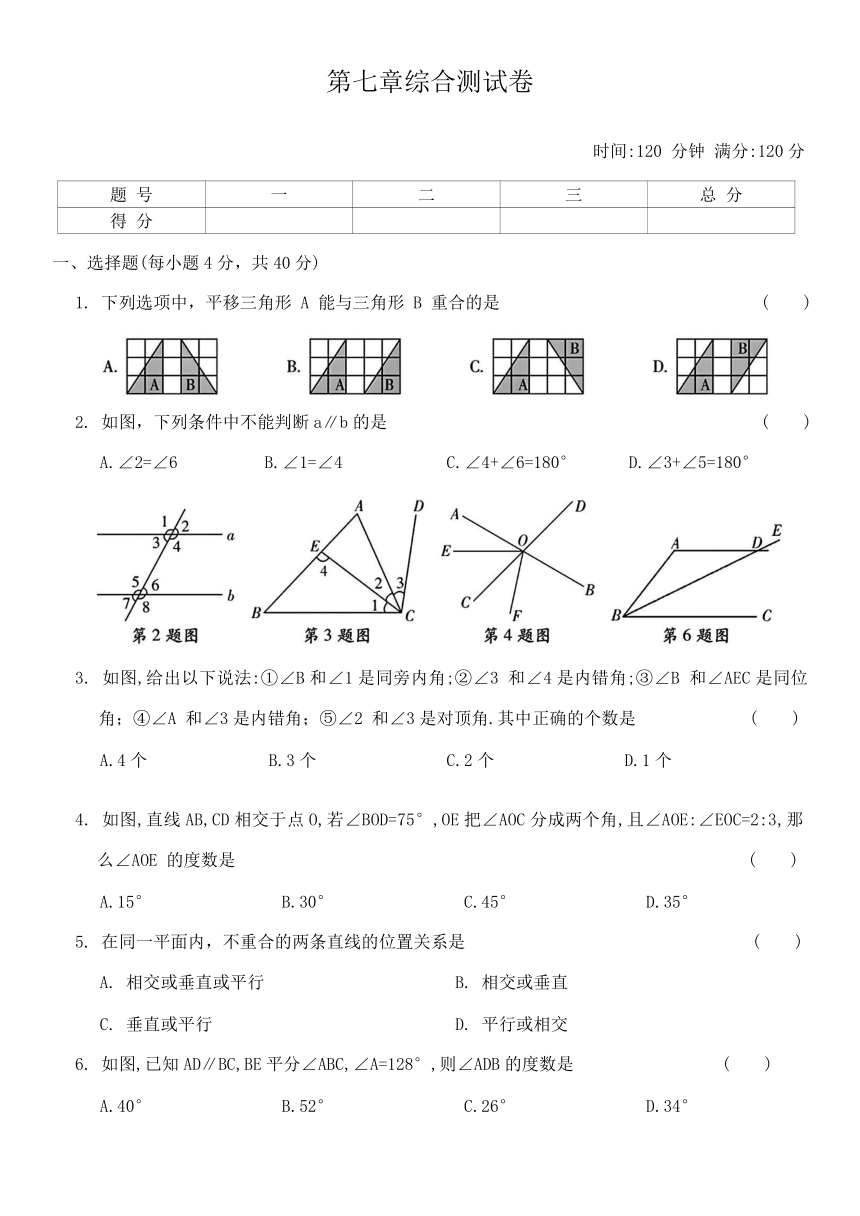
1. 下列选项中,平移三角形 A 能与三角形 B 重合的是 ( )
2. 如图,下列条件中不能判断a∥b的是 ( )
A.∠2=∠6 B.∠1=∠4 C.∠4+∠6=180° D.∠3+∠5=180°
3. 如图,给出以下说法:①∠B和∠1是同旁内角;②∠3 和∠4是内错角;③∠B 和∠AEC是同位角;④∠A 和∠3是内错角;⑤∠2 和∠3是对顶角.其中正确的个数是 ( )
A.4个 B.3个 C.2个 D.1个
4. 如图,直线AB,CD相交于点O,若∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3,那么∠AOE 的度数是 ( )
A.15° B.30° C.45° D.35°
5. 在同一平面内,不重合的两条直线的位置关系是 ( )
A. 相交或垂直或平行 B. 相交或垂直
C. 垂直或平行 D. 平行或相交
6. 如图,已知AD∥BC,BE平分∠ABC,∠A=128°,则∠ADB的度数是 ( )
A.40° B.52° C.26° D.34°
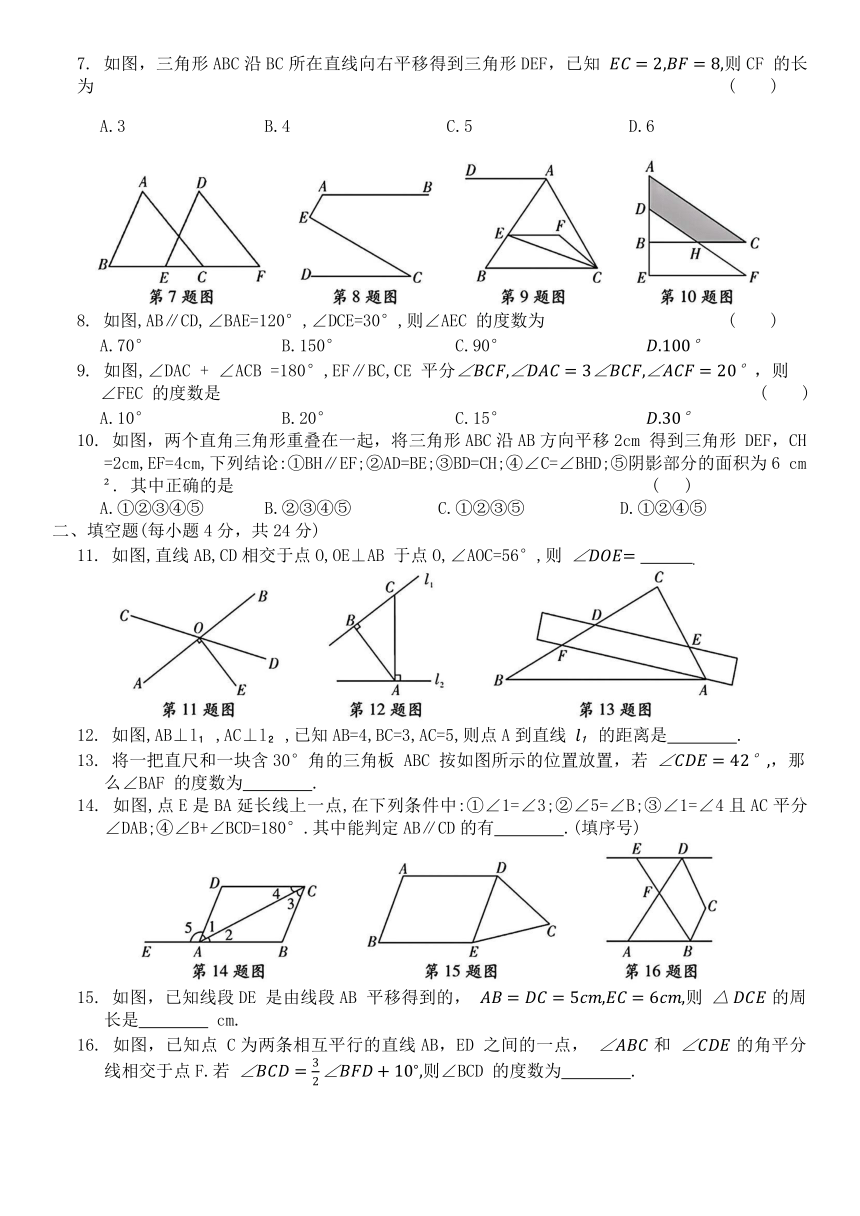
7. 如图,三角形ABC沿BC所在直线向右平移得到三角形DEF,已知 则CF 的长为 ( )
A.3 B.4 C.5 D.6
8. 如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC 的度数为 ( )
A.70° B.150° C.90°
9. 如图,∠DAC + ∠ACB =180°,EF∥BC,CE 平分,则 ∠FEC 的度数是 ( )
A.10° B.20° C.15°
10. 如图,两个直角三角形重叠在一起,将三角形ABC沿AB方向平移2cm 得到三角形 DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6 cm . 其中正确的是 ( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
二、填空题(每小题4分,共24分)
11. 如图,直线AB,CD相交于点O,OE⊥AB 于点O,∠AOC=56°,则
12. 如图,AB⊥l ,AC⊥l ,已知AB=4,BC=3,AC=5,则点A到直线 的距离是 .
13. 将一把直尺和一块含30°角的三角板 ABC 按如图所示的位置放置,若 ,那么∠BAF 的度数为 .
14. 如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°.其中能判定AB∥CD的有 .(填序号)
15. 如图,已知线段DE 是由线段AB 平移得到的, 则 的周长是 cm.
16. 如图,已知点 C为两条相互平行的直线AB,ED 之间的一点, 和 的角平分线相交于点F.若 则∠BCD 的度数为 .
三、解答题(共56分)
17.(6分)已知点B,E,C,F在同一直线上, 求证:
18.(6分)如图,直线AB,CD 相交于点O,OE平分 求∠EOF 的度数.
19. (6分)如图,点E在直线BH,DC之间,点A 为BH上一点,且 求证:
20. (7分)如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有 ,请解释进入潜望镜的光线l为什么和离开潜望镜的光线 m是平行的.
21. (9分)如图,直线AB,CD 相交于点O,OD平分∠BOE,OF平分∠AOE.
(1)若∠BOE=58°,∠AOE=122°,判断OF与OD 的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
22. (10分)如图,已知点E在直线DC上,射线EF平分∠AED,过点 E作EB⊥EF,G为射线EC上一点,连接BG,且∠EBG+∠BEG=90°.
(1)求证:∠DEF=∠EBG.
(2)若∠EBG=∠A,试判断AB与EF的位置关系,并说明理由.
23. (12分)如图,直线CB∥OA,∠C=∠OAB=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)直线OC与AB有何位置关系 请说明理由.
(2)求∠EOB 的度数.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA 若存在,求出其度数;若不存在,说明理由.
第七章综合测试卷
1. B 2. B 3. B 4. B 5. D 6. C 7. A 8. C 9. B 10. D11.34° 12.4 13.12° 14.③④ 15.16 16.160°
17. 证明:∵AB∥DE,∴∠B=∠DEF,∵∠A=∠D,∠ACB=180°-∠A-∠B,∠DFE=180°-∠D-∠DEF,
∴∠ACB=∠DFE,∴AC∥DF.
18. 解:∵∠AOC与∠BOD是对顶角,∠BOD=62°,∴∠AOC=62°.∵ OE 平分∠ 31°. ∵ OF ⊥OD,∴ ∠COF = ∠DOF =90°.∴ ∠EOF +∠COE=90°.∴∠EOF=90°-∠COE=90°-31°=59°.
19. 证明:过点 E 作 EF∥BH,∴ ∠HAE =∠AEF.
∵AE⊥CE,∴ ∠AEC =90°, 即
∠CEF=90°.
∴ ∠CEF =90°-∠HAE.∵ ∠ECG = 90° - ∠HAE,
∴ ∠CEF =∠ECG.∴EF∥DG.
∵EF∥BH,∴BH∥DG.
20. 解:∵
=∠
即∠5=∠6.
∴l∥m.∴进入潜望镜的光线l和离开潜望镜的光线m是平行的.
21. 解:(1)OF⊥OD. 证明如下:
∵OD 平分∠BOE,OF 平分
∠EOD=61°+29°=90°,∴OF⊥OD.
C与∠BOD 是对顶角,∴∠AOC=∠BOD =30°.∵ OD 平分∠BOE,∴ ∠BOE =2∠BOD=60°.∴∠AOE=180°-∠BOE=120°,又OF平分
22. (1)证明:∵ EB⊥EF,∴ ∠FEB=90°,∴∠DEF+∠BEG=180° – 90° = 90°. ∵ ∠EBG + ∠BEG = 90°,∴ ∠DEF=∠EBG.
(2)解:AB∥EF.理由如下:∵ EF 平分∠AED,∴ ∠AEF =∠DEF,∵∠EBG=∠A,∠DEF=∠EBG,∴∠A=∠DEF=∠AEF,∴AB∥EF.
23. 解:(1)AB∥OC,理由如下:∵CB∥OA,∴∠ABC+∠OAB =180°,∵ ∠C=∠OAB =100°,∴ ∠C+∠ABC=180°,∴AB∥OC.
(2)∵ CB∥OA,∠C =100°,∴ ∠AOC =80°. 又∠FOB =∠AOB,OE 平分∠COF,∴ ∠EOB = ∠BOF + ∠EOF =
(3)存在. 理由如下:∵ ∠COE + ∠CEO + ∠C = 180°,∠BOA +∠OAB + ∠ABO = 180°,∠OEC = ∠OBA,∠C =∠OAB,∴∠COE=∠AOB,∴OB,OE,OF是∠AOC的四等分线, 180°-∠C--∠COE=180°-100°-20°=60°,故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 下列选项中,平移三角形 A 能与三角形 B 重合的是 ( )
2. 如图,下列条件中不能判断a∥b的是 ( )
A.∠2=∠6 B.∠1=∠4 C.∠4+∠6=180° D.∠3+∠5=180°
3. 如图,给出以下说法:①∠B和∠1是同旁内角;②∠3 和∠4是内错角;③∠B 和∠AEC是同位角;④∠A 和∠3是内错角;⑤∠2 和∠3是对顶角.其中正确的个数是 ( )
A.4个 B.3个 C.2个 D.1个
4. 如图,直线AB,CD相交于点O,若∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3,那么∠AOE 的度数是 ( )
A.15° B.30° C.45° D.35°
5. 在同一平面内,不重合的两条直线的位置关系是 ( )
A. 相交或垂直或平行 B. 相交或垂直
C. 垂直或平行 D. 平行或相交
6. 如图,已知AD∥BC,BE平分∠ABC,∠A=128°,则∠ADB的度数是 ( )
A.40° B.52° C.26° D.34°
7. 如图,三角形ABC沿BC所在直线向右平移得到三角形DEF,已知 则CF 的长为 ( )
A.3 B.4 C.5 D.6
8. 如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC 的度数为 ( )
A.70° B.150° C.90°
9. 如图,∠DAC + ∠ACB =180°,EF∥BC,CE 平分,则 ∠FEC 的度数是 ( )
A.10° B.20° C.15°
10. 如图,两个直角三角形重叠在一起,将三角形ABC沿AB方向平移2cm 得到三角形 DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6 cm . 其中正确的是 ( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
二、填空题(每小题4分,共24分)
11. 如图,直线AB,CD相交于点O,OE⊥AB 于点O,∠AOC=56°,则
12. 如图,AB⊥l ,AC⊥l ,已知AB=4,BC=3,AC=5,则点A到直线 的距离是 .
13. 将一把直尺和一块含30°角的三角板 ABC 按如图所示的位置放置,若 ,那么∠BAF 的度数为 .
14. 如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°.其中能判定AB∥CD的有 .(填序号)
15. 如图,已知线段DE 是由线段AB 平移得到的, 则 的周长是 cm.
16. 如图,已知点 C为两条相互平行的直线AB,ED 之间的一点, 和 的角平分线相交于点F.若 则∠BCD 的度数为 .
三、解答题(共56分)
17.(6分)已知点B,E,C,F在同一直线上, 求证:
18.(6分)如图,直线AB,CD 相交于点O,OE平分 求∠EOF 的度数.
19. (6分)如图,点E在直线BH,DC之间,点A 为BH上一点,且 求证:
20. (7分)如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有 ,请解释进入潜望镜的光线l为什么和离开潜望镜的光线 m是平行的.
21. (9分)如图,直线AB,CD 相交于点O,OD平分∠BOE,OF平分∠AOE.
(1)若∠BOE=58°,∠AOE=122°,判断OF与OD 的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
22. (10分)如图,已知点E在直线DC上,射线EF平分∠AED,过点 E作EB⊥EF,G为射线EC上一点,连接BG,且∠EBG+∠BEG=90°.
(1)求证:∠DEF=∠EBG.
(2)若∠EBG=∠A,试判断AB与EF的位置关系,并说明理由.
23. (12分)如图,直线CB∥OA,∠C=∠OAB=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)直线OC与AB有何位置关系 请说明理由.
(2)求∠EOB 的度数.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA 若存在,求出其度数;若不存在,说明理由.
第七章综合测试卷
1. B 2. B 3. B 4. B 5. D 6. C 7. A 8. C 9. B 10. D11.34° 12.4 13.12° 14.③④ 15.16 16.160°
17. 证明:∵AB∥DE,∴∠B=∠DEF,∵∠A=∠D,∠ACB=180°-∠A-∠B,∠DFE=180°-∠D-∠DEF,
∴∠ACB=∠DFE,∴AC∥DF.
18. 解:∵∠AOC与∠BOD是对顶角,∠BOD=62°,∴∠AOC=62°.∵ OE 平分∠ 31°. ∵ OF ⊥OD,∴ ∠COF = ∠DOF =90°.∴ ∠EOF +∠COE=90°.∴∠EOF=90°-∠COE=90°-31°=59°.
19. 证明:过点 E 作 EF∥BH,∴ ∠HAE =∠AEF.
∵AE⊥CE,∴ ∠AEC =90°, 即
∠CEF=90°.
∴ ∠CEF =90°-∠HAE.∵ ∠ECG = 90° - ∠HAE,
∴ ∠CEF =∠ECG.∴EF∥DG.
∵EF∥BH,∴BH∥DG.
20. 解:∵
=∠
即∠5=∠6.
∴l∥m.∴进入潜望镜的光线l和离开潜望镜的光线m是平行的.
21. 解:(1)OF⊥OD. 证明如下:
∵OD 平分∠BOE,OF 平分
∠EOD=61°+29°=90°,∴OF⊥OD.
C与∠BOD 是对顶角,∴∠AOC=∠BOD =30°.∵ OD 平分∠BOE,∴ ∠BOE =2∠BOD=60°.∴∠AOE=180°-∠BOE=120°,又OF平分
22. (1)证明:∵ EB⊥EF,∴ ∠FEB=90°,∴∠DEF+∠BEG=180° – 90° = 90°. ∵ ∠EBG + ∠BEG = 90°,∴ ∠DEF=∠EBG.
(2)解:AB∥EF.理由如下:∵ EF 平分∠AED,∴ ∠AEF =∠DEF,∵∠EBG=∠A,∠DEF=∠EBG,∴∠A=∠DEF=∠AEF,∴AB∥EF.
23. 解:(1)AB∥OC,理由如下:∵CB∥OA,∴∠ABC+∠OAB =180°,∵ ∠C=∠OAB =100°,∴ ∠C+∠ABC=180°,∴AB∥OC.
(2)∵ CB∥OA,∠C =100°,∴ ∠AOC =80°. 又∠FOB =∠AOB,OE 平分∠COF,∴ ∠EOB = ∠BOF + ∠EOF =
(3)存在. 理由如下:∵ ∠COE + ∠CEO + ∠C = 180°,∠BOA +∠OAB + ∠ABO = 180°,∠OEC = ∠OBA,∠C =∠OAB,∴∠COE=∠AOB,∴OB,OE,OF是∠AOC的四等分线, 180°-∠C--∠COE=180°-100°-20°=60°,故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
同课章节目录
