5.2.1平行线课件(共15张PPT)
图片预览




文档简介
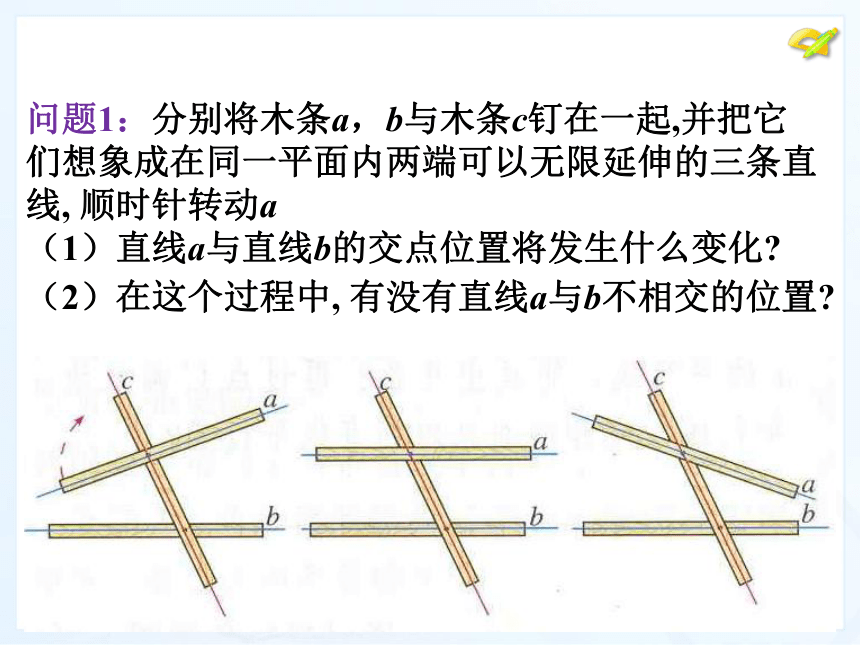
课件15张PPT。5.2.1 平行线问题1:分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线, 顺时针转动a
(1)直线a与直线b的交点位置将发生什么变化?(2)在这个过程中, 有没有直线a与b不相交的位置?平行概念: 同一平面内, 不相交的两条直
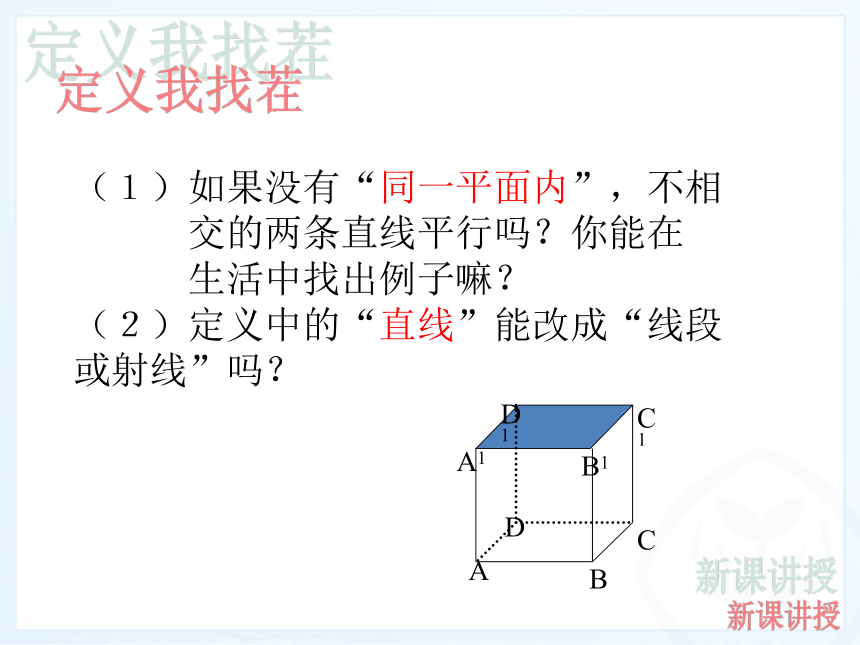
线叫做平行线.我们通常用“//”表示平行 记作:AB ∥ CD 记作:m ∥ n读作: “ m平行于n ” 读作: “AB 平行于 CD” (1)如果没有“同一平面内”,不相
交的两条直线平行吗?你能在
生活中找出例子嘛?
(2)定义中的“直线”能改成“线段或射线”吗?定义我找茬新课讲授问题2:同一平面内,两条直线存在哪些位置关系?问题3:平行线在生活中很常见, 你能举出一些例子吗? 相交和平行问题4:如何画平行线呢?给一条直线a,
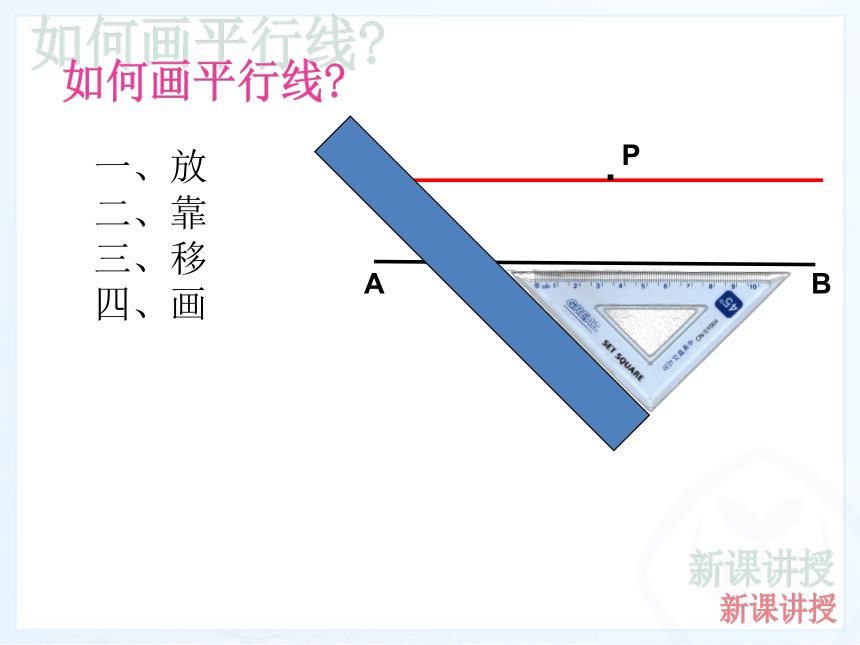
你能画出直线a的平行线吗?· A B P如何画平行线?一、放
二、靠
三、移
四、画新课讲授AB可以画多少条平行线呢?无数条问题5:过点B画直线a的平行线,能画出几条?(三)平行公理及其推论平行公理:经过直线外一点,有且只有一条直线与这条直线平行.问题6:再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?(三)平行公理及其推论平行公理推论:如果两条直线都与第三条直线平行,那么这条直线也互相平行.实质是:平行具有传递性如果b∥a,c∥a,那么b∥c. 1、判断正误:(1)两条不相交的直线叫做平行线。
(2)有且只有一个公共点的两直线
是相交直线。
(3)在同一平面内的两条直线一定
平行。
(4)一个平面内的两条直线,必把
这个平面分为四部分。( × ) ( √) ( × ) ( × ) 随堂练一练2、下列语句中,正确的个数是 ( )
(1)不相交的两条直线是平行线
(2)同一平面内,两直线的位置关系有两种,即相交或平行
(3)若线段AB与CD没有交点则AB//CD
(4)若a//b,b//c,则a 与c不相交
(A)1个 (B)2个 (C)3个 (D)4个B3、下列说法正确的是( )
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行D随堂练一练3、如图,长方体的各棱中,与AA1平行的条数有( )
A、1 B、2 C、3 D、4C随堂练一练4、已知直线a与b都经过点P,并且a//c,b//c,那
么a与b必重合,这是因为1.平面内两条直线有哪些位置关系?
2.平行公理及其推论的内容是什么? (四)归纳小结(五)布置作业教科书第12页练习
(1)直线a与直线b的交点位置将发生什么变化?(2)在这个过程中, 有没有直线a与b不相交的位置?平行概念: 同一平面内, 不相交的两条直
线叫做平行线.我们通常用“//”表示平行 记作:AB ∥ CD 记作:m ∥ n读作: “ m平行于n ” 读作: “AB 平行于 CD” (1)如果没有“同一平面内”,不相
交的两条直线平行吗?你能在
生活中找出例子嘛?
(2)定义中的“直线”能改成“线段或射线”吗?定义我找茬新课讲授问题2:同一平面内,两条直线存在哪些位置关系?问题3:平行线在生活中很常见, 你能举出一些例子吗? 相交和平行问题4:如何画平行线呢?给一条直线a,
你能画出直线a的平行线吗?· A B P如何画平行线?一、放
二、靠
三、移
四、画新课讲授AB可以画多少条平行线呢?无数条问题5:过点B画直线a的平行线,能画出几条?(三)平行公理及其推论平行公理:经过直线外一点,有且只有一条直线与这条直线平行.问题6:再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?(三)平行公理及其推论平行公理推论:如果两条直线都与第三条直线平行,那么这条直线也互相平行.实质是:平行具有传递性如果b∥a,c∥a,那么b∥c. 1、判断正误:(1)两条不相交的直线叫做平行线。
(2)有且只有一个公共点的两直线
是相交直线。
(3)在同一平面内的两条直线一定
平行。
(4)一个平面内的两条直线,必把
这个平面分为四部分。( × ) ( √) ( × ) ( × ) 随堂练一练2、下列语句中,正确的个数是 ( )
(1)不相交的两条直线是平行线
(2)同一平面内,两直线的位置关系有两种,即相交或平行
(3)若线段AB与CD没有交点则AB//CD
(4)若a//b,b//c,则a 与c不相交
(A)1个 (B)2个 (C)3个 (D)4个B3、下列说法正确的是( )
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行D随堂练一练3、如图,长方体的各棱中,与AA1平行的条数有( )
A、1 B、2 C、3 D、4C随堂练一练4、已知直线a与b都经过点P,并且a//c,b//c,那
么a与b必重合,这是因为1.平面内两条直线有哪些位置关系?
2.平行公理及其推论的内容是什么? (四)归纳小结(五)布置作业教科书第12页练习
