冀教版七年级下册提取公因式法举例

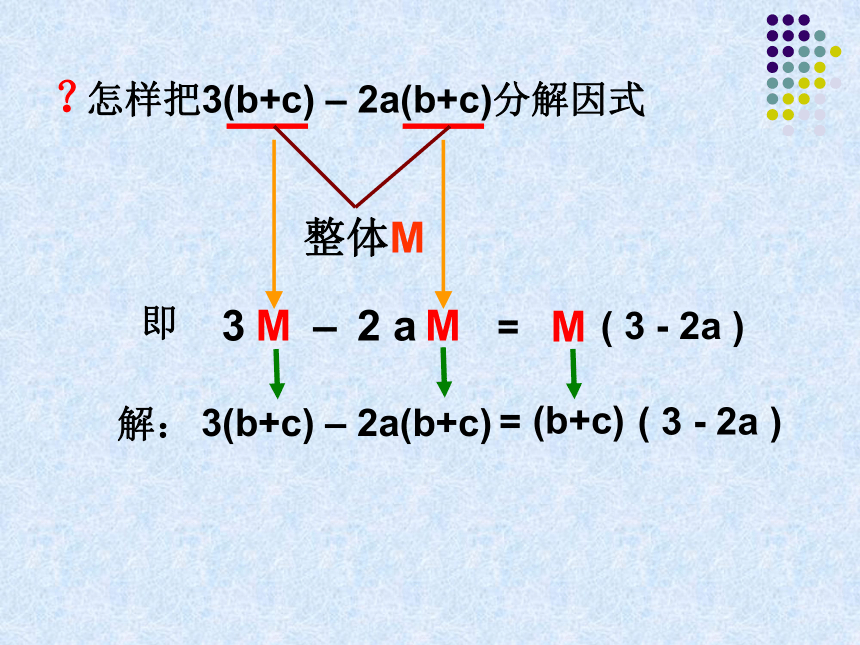
课件15张PPT。提取公因式法举例3 M – 2 a M 能用提取公因式法分解吗？M M 能公因式是什么？是 M怎样把3(b+c) – 2a(b+c)分解因式？整体M3即MM2 a–3(b+c) – 2a(b+c)( 3 - 2a )解：=(b+c)=M( 3 - 2a )例1 把 3 ( x – y ) 2 – ( x – y ) 3 分解因式最大
公因数1相同因式
最低次幂( x – y ) 23 ( x – y ) 2 – ( x – y ) 3 ( x – y ) 2= ( x – y ) 2 ( 3 – x + y )[ 3 – ( x – y ) ]解：=所以，公因式是 ( x – y ) 2 须化简? a ( x + y ) + b ( x + y )
? x ( a + 5 ) – y ( a + 5 )
? 3m ( p – 2 ) + 15n ( p – 2 )
? 3a ( x – y + z ) – 5b ( x – y + z )
? 2 a2 (a – b) 2 – 4a ( a – b) 3
? 7 ( x – 3 ) – x ( 3 – x )下列各式的公因式分别是什么？找一找：( x + y ) ( a + 5 )3 ( p – 2 )( x – y + z )2a( a – b) 2? y – x = ( y – x )
? b – a = ( a – b )
? – x 2 + y 2 = ( x 2 – y 2)
? – x 2 – y 2 = ( x 2 + y 2 )
? – m 2 + n 2 = ( n 2 – m 2)填符号: 例2 把 7 ( x – 3 ) – x ( 3 – x ) 分解因式.7 ( x – 3 ) + x ( x – 3 ) 解：7 ( x – 3 ) – x ( 3 – x )==( x – 3 ) ( 7 + x ).想一想 ( a – b )1 = – (b – a )1( a – b )2 = (b – a )2 ( a – b )3 = – (b – a )3( a – b )4 = (b – a )4…… ……从中你能发现什么规律？例3 把 18b ( b – a )2 – 12 ( a – b )3分解因式.例3 把 18b ( b – a )2 – 12 ( a – b )3分解因式.18b ( b – a )2 – 12 ( a – b )318b ( a – b )2 – 12 ( a – b )36( a – b )26( a – b )2 ( 3b – 2a + 2b )6( a – b )2 ( 5b – 2a )====解：∴( b – a )2=[– ( a – b )]2=( a – b )2∵[ 3b – 2 ( a – b ) ]例3 把 18b ( b – a )2 – 12 ( a – b )3分解因式.18b ( b – a )2 – 12 ( a – b )318b ( b – a )2 + 12 ( b – a )36( b – a )26( b – a )2 ( 3b + 2b –2a )6( b – a )2 ( 5b – 2a )====解：∴–12( b – a )3=+12( b – a )3∵[ 3b + 2 ( b – a ) ]本节结构:(2)遇只差一个“ – ”号的因式，可统一形式后，再用提取公因式法分解因式，(3)分解因式时，最后应将每一个因式化简.b – a = –(a – b); (b – a)2= (a – b)2;(b – a)3= –(a – b)3特别要注意以下的变形：一个数一个字母单项式多项式（1）公因式 具有广泛性“整体”看成练习1.把下列各式分解因式:
? x (a + b ) + y ( a + b )
? 2x ( a – b ) + b – a
? – a2( a + b ) + ( a + b )3
? xy ( x – y ) – x ( y – x )22.计算 :
21 ? 3.14 + 62 ? 3.14 + 17 ? 3.141、提取公因式法分解因式的基本公式是：am + bm + cm = m (a + b + c)其中a,b,c,m可以是单项式，也可以是多项式，公因式具有广泛性。2、要学会以下的变形：b – a = –(a – b); (b – a)2= (a – b)2;(b – a)3= –(a – b)34、常用的数学思想方法整体思想小结3、注意：?化简每个因式 ?分解彻底作业：作业本再 见