人教版(2024)数学七年级下册 第八、九章综合测试卷(含答案)
文档属性
| 名称 | 人教版(2024)数学七年级下册 第八、九章综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 160.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 10:56:38 | ||
图片预览


文档简介
第八、九章综合测试卷
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 下列实数中最小的是 ( )
A. -π B. - 3 D. - 2
的平方根是 ( )
A.9 B.9或-9 C.3 D.3或-3
3. 若a>0,则点M(a,-7)在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 下列说法中,正确的是 ( )
A.(-2) 的立方根是-2 B.0.4的算术平方根是0.2
的立方根是4 D.16的平方根是4
5. 已知点A的坐标为(1,3),将点A向左平移1个单位长度,再向下平移4个单位长度,则点A的对应点的坐标为 ( )
A.(5,3) B.(-1,-2) C.(-1,-1) D.(0,-1)
6. 若实数 的小数部分为a, 的小数部分为b,则a-b的值为 ( )
A.
7. 在平面直角坐标系中,线段AB的端点分别为A(2,0),B(0,4),将线段AB平移到A B ,且点 A 的坐标为(8,4),则点 B 的坐标为 ( )
A.(7,6) B.(6,7) C.(6,8) D.(8,6)
8. 如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若p+m=0,则m,n,p,q四个数中,绝对值最小的一个是 ( )
A. m B. n C. p D. q
9. 已知 min{ ,x ,x}表示取三个数中最小的那个数,例如,当x=9, min{ ,x ,x} = min{ ,9 ,9}=3,当 时,x的值为 ( )
A. B. C. D.
10. 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2025个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是 ( )
A.(1,0) B.(0,1)
C.(-1,1) D.(-1,-2)
二、填空题(每小题3分,共18分)
11. 在实数 中,无理数是 .
12. 在平面直角坐标系中,点 在第 象限.
13. 已知实数x的两个平方根分别为2a+1和3-4a,实数y的立方根为-a,则 的值为 .
14. 在平面直角坐标系中,若点M(1-m,m+2)与点N(2m+3,m+2)之间的距离是5,则m= .
15. 对于两个不相等的实数a,b,定义一种新运算: 例如: 那么15*(6*3)= .
16. 如图①,某广场地面是用A,B,C三种类型地砖平铺而成的,三种类型地砖上表面图案如图②所示.现在用有序数对表示每一块地砖的位置:第一行的第一块(A型)地砖记作(1,1),第二块(B型)地砖记作(2,1)...若(m,n)位置恰好为A型地砖,则正整数m,n须满足的条件是 .
三、解答题(共62分)
17. (6分)求下列各式中x的值.
18. (8分)计算:
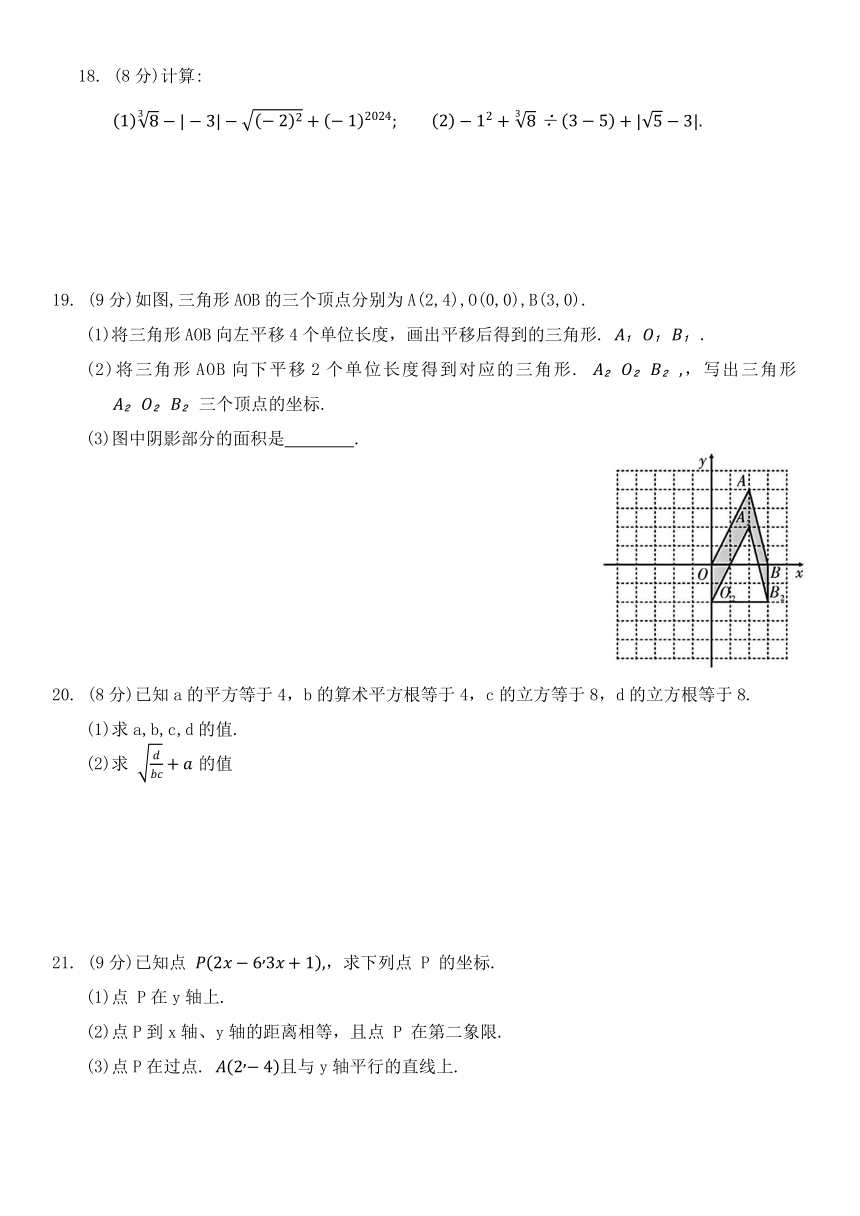
19. (9分)如图,三角形AOB的三个顶点分别为A(2,4),O(0,0),B(3,0).
(1)将三角形AOB向左平移4个单位长度,画出平移后得到的三角形.
(2)将三角形AOB向下平移2个单位长度得到对应的三角形. ,写出三角形 三个顶点的坐标.
(3)图中阴影部分的面积是 .
20. (8分)已知a的平方等于4,b的算术平方根等于4,c的立方等于8,d的立方根等于8.
(1)求a,b,c,d的值.
(2)求 的值
21. (9分)已知点 ,求下列点 P 的坐标.
(1)点 P在y轴上.
(2)点P到x轴、y轴的距离相等,且点 P 在第二象限.
(3)点P在过点. 且与y轴平行的直线上.
22. (10分)阅读下面文字,然后解答问题.
大家知道 是无理数,而无理数是无限不循环小数,所以 的小数部分我们不可能全部写出来,由于 的整数部分是1,用 减去它的整数部分,差就是它的小数部分,因此 的小数部分可用 表示. 由此我们得到一个真命题:如果 其中x是整数,且 那么x
请解答下列问题:
(1)如果 其中a是整数,且 那么
(2)已知 其中m是整数,且 求 的值.
23. (12分)先阅读下列一段文字,再回答后面的问题:已知在平面直角坐标系内两点 其两点间的距离 同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为 或
(1)已知A(1,3),E ,试求A,B两点间的距离.
(2)已知线段 轴, ,若点M 的坐标为 ,试求点N的坐标.
(3)已知一个三角形各顶点坐标为D(0,6),E(-3,2),F(3,2),你能判定此三角形的形状吗 说明理由.
第八、九章综合测试卷
1. A 2. D 3. D 4. A 5. D 6. D 7. C 8. B 9. C 10. B 12. 四 13.3 或1
16. m,n同为奇数或m,n同为偶数
17. 解:(1)开方得x-1 =2 或: 解得 或x =
(2)方程整理得 开立方得 解得
(3)方程整理得 开立方得
18. 解:(1)原式
(2)原式:
19. 解:(1)如图所示,三角形. 即为所求.
(2)由图知,
(3)阴影部分的面积为 故答案为:6.
20. 解:
(2)当 时,
当 时, 的值为6或2.
21. 解:(1)∵点P(2x-6,3x+1),且点 P在y轴上,∴2x-6=0,解得x=3.
∴3x+1=10,∴点P的坐标为(0,10).
(2)∵点P(2x-6,3x+1),点 P到x轴、y轴的距离相等,且点 P在第二象限,
∴2x-6=--(3x+1),解得x=1,∴2x-6=-4,3x+1=4,∴点 P的坐标为( - 4,4).
(3)∵点P(2x-6,3x+1)在过点A(2,-4)且与y轴平行的直线上,∴2x-6=2,解得x=4,∴3x+1=13,∴点 P的坐标为(2,13).
22. 解: 其中a是整数,且0故答案为:2
其中m是整数,且0则|
23. 解:(1)A,B两点间的距离
(2)∵线段MN∥y轴,∴M,N的横坐标相同,设N(2,t),由题意,得|t+1|=4,解得t=3或-5,∴点N的坐标为(2,3)或(2,-5).
(3)三角形 DEF 为等腰三角形.理由如下:
∵ D (0, 6), E ( - 3, 2), F (3, 2),
∴ DE =
,∴三角形DEF 为等腰三角形.
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 下列实数中最小的是 ( )
A. -π B. - 3 D. - 2
的平方根是 ( )
A.9 B.9或-9 C.3 D.3或-3
3. 若a>0,则点M(a,-7)在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 下列说法中,正确的是 ( )
A.(-2) 的立方根是-2 B.0.4的算术平方根是0.2
的立方根是4 D.16的平方根是4
5. 已知点A的坐标为(1,3),将点A向左平移1个单位长度,再向下平移4个单位长度,则点A的对应点的坐标为 ( )
A.(5,3) B.(-1,-2) C.(-1,-1) D.(0,-1)
6. 若实数 的小数部分为a, 的小数部分为b,则a-b的值为 ( )
A.
7. 在平面直角坐标系中,线段AB的端点分别为A(2,0),B(0,4),将线段AB平移到A B ,且点 A 的坐标为(8,4),则点 B 的坐标为 ( )
A.(7,6) B.(6,7) C.(6,8) D.(8,6)
8. 如图,四个实数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若p+m=0,则m,n,p,q四个数中,绝对值最小的一个是 ( )
A. m B. n C. p D. q
9. 已知 min{ ,x ,x}表示取三个数中最小的那个数,例如,当x=9, min{ ,x ,x} = min{ ,9 ,9}=3,当 时,x的值为 ( )
A. B. C. D.
10. 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2025个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是 ( )
A.(1,0) B.(0,1)
C.(-1,1) D.(-1,-2)
二、填空题(每小题3分,共18分)
11. 在实数 中,无理数是 .
12. 在平面直角坐标系中,点 在第 象限.
13. 已知实数x的两个平方根分别为2a+1和3-4a,实数y的立方根为-a,则 的值为 .
14. 在平面直角坐标系中,若点M(1-m,m+2)与点N(2m+3,m+2)之间的距离是5,则m= .
15. 对于两个不相等的实数a,b,定义一种新运算: 例如: 那么15*(6*3)= .
16. 如图①,某广场地面是用A,B,C三种类型地砖平铺而成的,三种类型地砖上表面图案如图②所示.现在用有序数对表示每一块地砖的位置:第一行的第一块(A型)地砖记作(1,1),第二块(B型)地砖记作(2,1)...若(m,n)位置恰好为A型地砖,则正整数m,n须满足的条件是 .
三、解答题(共62分)
17. (6分)求下列各式中x的值.
18. (8分)计算:
19. (9分)如图,三角形AOB的三个顶点分别为A(2,4),O(0,0),B(3,0).
(1)将三角形AOB向左平移4个单位长度,画出平移后得到的三角形.
(2)将三角形AOB向下平移2个单位长度得到对应的三角形. ,写出三角形 三个顶点的坐标.
(3)图中阴影部分的面积是 .
20. (8分)已知a的平方等于4,b的算术平方根等于4,c的立方等于8,d的立方根等于8.
(1)求a,b,c,d的值.
(2)求 的值
21. (9分)已知点 ,求下列点 P 的坐标.
(1)点 P在y轴上.
(2)点P到x轴、y轴的距离相等,且点 P 在第二象限.
(3)点P在过点. 且与y轴平行的直线上.
22. (10分)阅读下面文字,然后解答问题.
大家知道 是无理数,而无理数是无限不循环小数,所以 的小数部分我们不可能全部写出来,由于 的整数部分是1,用 减去它的整数部分,差就是它的小数部分,因此 的小数部分可用 表示. 由此我们得到一个真命题:如果 其中x是整数,且 那么x
请解答下列问题:
(1)如果 其中a是整数,且 那么
(2)已知 其中m是整数,且 求 的值.
23. (12分)先阅读下列一段文字,再回答后面的问题:已知在平面直角坐标系内两点 其两点间的距离 同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为 或
(1)已知A(1,3),E ,试求A,B两点间的距离.
(2)已知线段 轴, ,若点M 的坐标为 ,试求点N的坐标.
(3)已知一个三角形各顶点坐标为D(0,6),E(-3,2),F(3,2),你能判定此三角形的形状吗 说明理由.
第八、九章综合测试卷
1. A 2. D 3. D 4. A 5. D 6. D 7. C 8. B 9. C 10. B 12. 四 13.3 或1
16. m,n同为奇数或m,n同为偶数
17. 解:(1)开方得x-1 =2 或: 解得 或x =
(2)方程整理得 开立方得 解得
(3)方程整理得 开立方得
18. 解:(1)原式
(2)原式:
19. 解:(1)如图所示,三角形. 即为所求.
(2)由图知,
(3)阴影部分的面积为 故答案为:6.
20. 解:
(2)当 时,
当 时, 的值为6或2.
21. 解:(1)∵点P(2x-6,3x+1),且点 P在y轴上,∴2x-6=0,解得x=3.
∴3x+1=10,∴点P的坐标为(0,10).
(2)∵点P(2x-6,3x+1),点 P到x轴、y轴的距离相等,且点 P在第二象限,
∴2x-6=--(3x+1),解得x=1,∴2x-6=-4,3x+1=4,∴点 P的坐标为( - 4,4).
(3)∵点P(2x-6,3x+1)在过点A(2,-4)且与y轴平行的直线上,∴2x-6=2,解得x=4,∴3x+1=13,∴点 P的坐标为(2,13).
22. 解: 其中a是整数,且0
其中m是整数,且0
23. 解:(1)A,B两点间的距离
(2)∵线段MN∥y轴,∴M,N的横坐标相同,设N(2,t),由题意,得|t+1|=4,解得t=3或-5,∴点N的坐标为(2,3)或(2,-5).
(3)三角形 DEF 为等腰三角形.理由如下:
∵ D (0, 6), E ( - 3, 2), F (3, 2),
∴ DE =
,∴三角形DEF 为等腰三角形.
同课章节目录
