人教版(2024)数学七年级下册 专项训练卷(一)相交线与平行线、实数、平面直角坐标系(含答案)
文档属性
| 名称 | 人教版(2024)数学七年级下册 专项训练卷(一)相交线与平行线、实数、平面直角坐标系(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 200.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 11:07:52 | ||
图片预览



文档简介
专项训练卷(一)相交线与平行线、实数、平面直角坐标系
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
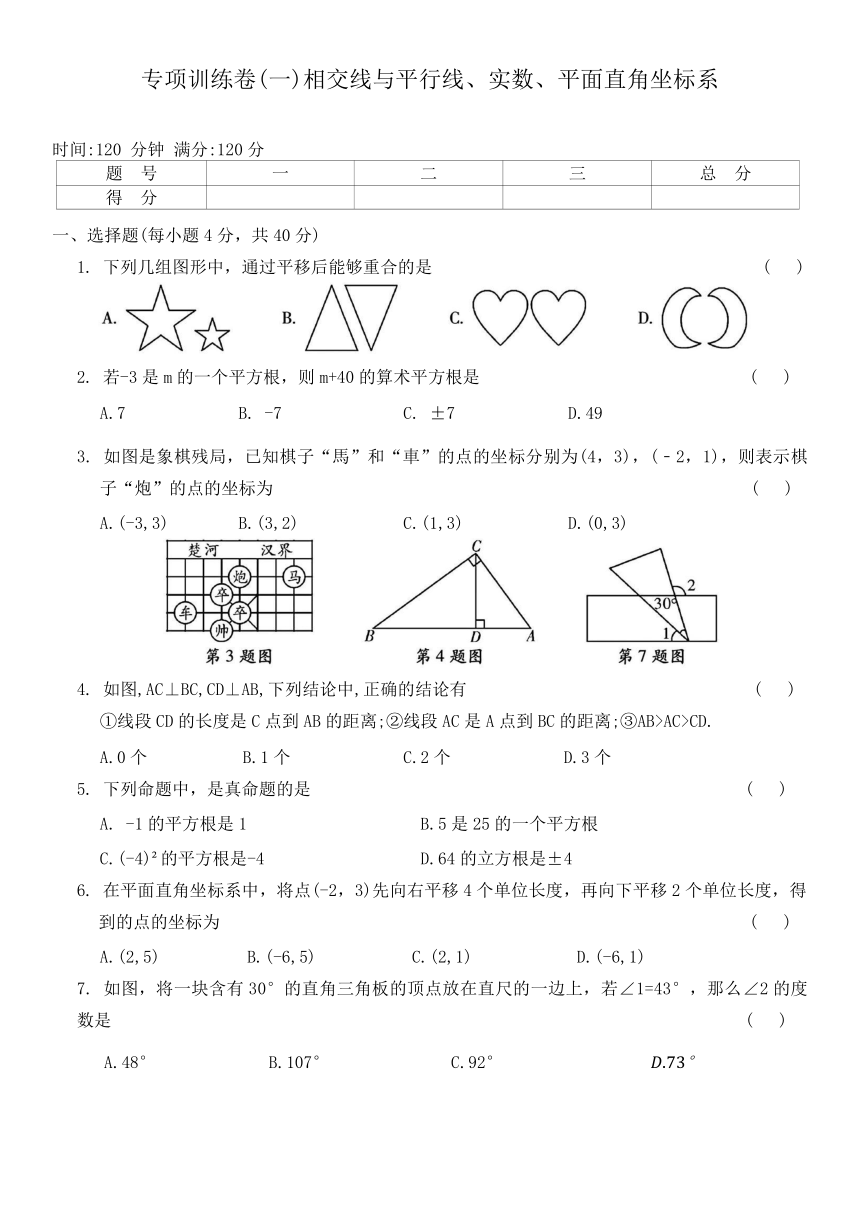
1. 下列几组图形中,通过平移后能够重合的是 ( )
2. 若-3是m的一个平方根,则m+40的算术平方根是 ( )
A.7 B. -7 C. ±7 D.49
3. 如图是象棋残局,已知棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为 ( )
A.(-3,3) B.(3,2) C.(1,3) D.(0,3)
4. 如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有 ( )
①线段CD的长度是C点到AB的距离;②线段AC是A点到BC的距离;③AB>AC>CD.
A.0个 B.1个 C.2个 D.3个
5. 下列命题中,是真命题的是 ( )
A. -1的平方根是1 B.5是25的一个平方根
C.(-4) 的平方根是-4 D.64的立方根是±4
6. 在平面直角坐标系中,将点(-2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为 ( )
A.(2,5) B.(-6,5) C.(2,1) D.(-6,1)
7. 如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=43°,那么∠2的度数是 ( )
A.48° B.107° C.92°
8. 已知x,y为正整数,且 则y 的最小值为 ( )
A.1 B.3 C.4 D.9
9. 在平面直角坐标系xOy中,对于点 P(x,y),我们把 叫做点 P 的友好点.已知点A 的友好点为A ,点A 的友好点为A ,点A 的友好点为 ,这样依次得到各点.若点 的坐标为(-3,2),设A (x,y),则x+y的值是 ( )
A. - 5 B. - 1 C.3 D.5
10. 如图,AD∥BC,∠D=∠ABC,点 E 是边 DC上一点,连接AE交BC的延长线于点 H,点F 是边 AB 上一点,使得 作∠FEH的平分线EG交BH于点G,若∠DEH=100°,则. 的度数为( )
A.30° B.40° C.50°
二、填空题(每小题4分,共24分)
的平方根是 , = .
12. 如果将点A(-3,-2)向右平移2个单位长度,再向上平移3个单位长度得到点 B,那么点B在第 象限.
13. 如图,直线 EF,CD 相交于点 O,OA⊥OB,OD 平分∠AOF,若. 则 = .
14. 实数a,b,c在数轴上的位置如图所示,则c-a-b 0(填“>”“<”或“=”).
15. 如图,直线AB∥CD,∠A=60°,∠D=40°,则∠E= .
16. 在平面直角坐标系中有一点P(a+1,a-3),其中a为任意实数,m,n分别表示点 P到x轴和y轴的距离,则m+n的最小值为 .
三、解答题(共56分)
17. (8分)求下列x的值:
18. (6分)定义如下的运算“ ”:对于任意实数a,b,都有 例如: 是 否存在负整数x,使得3 x的值小于4 若存在,求出所有的x;若不存在,请说明理由.
19. (8分)如图,在平面直角坐标系中,图中的网格是由边长相等的小正方形组成的,点A,B,C的坐标分别为
(1)请写出点D,E,F,G的坐标.
(2)求图中阴影部分(多边形ABCDEFG)的面积.
20. (10分)如图,直线AB,CD 相交于点O,过点O作 且OF平分.
(1)求证:
(2)求 的度数.
21. (12分)在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ ay),则称点Q是点P的“a级关联点”(其中a为常数,且a≠0),例如,点P(1,4)的“2级关联点”为Q(2×1+4,1+2×4),即Q(6,9).
(1)若点 P 的坐标为( -1,5),则它的“3级关联点”的坐标为 .
(2)若点 P 的“5级关联点”的坐标为(9,-3),求点 P 的坐标.
(3)若点P(m-1,2m)的“-3级关联点” P'位于坐标轴上,求点 P'的坐标.
22. (12分)如图1,AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE,DE所在直线交于点 E,∠ADC=80°.
(1)若∠ABC=50°,求∠BED 的度数.
(2)将线段BC沿DC方向平移,使得点B 在点A 的右侧,其他条件不变,若∠ABC=120°,求∠BED 的度数.
专项训练卷(一)
1. C 2. A 3. C 4. C 5. B 6. C 7. B 8. B 9. C 10. B11. ± -3 12. 二 13.36° 14. > 15.20° 16.4
17. 解:( 移项,得 开平方,得x--2=4或x-2=-4,解得x=6或x=-2.
开立方,得2x--1 = - 9,移项、合并得2x=-8,解得x= - 4.
18. 解:存在. 理由如下:
∵3 x=-3(3+x)+1=-8-3x;由题意-8-3x<4,解得x>-4.∴满足条件的负整数有-3,-2,--1.
19. 解:(1)点D,E,F,G的坐标分别为:(0,-2),(5,-3),(3,4),(-1,2).
(2)阴影部分(多边形ABCDEFG)的面积为:
70-5-7-8-3.5=46.5
20. (1)证明:∵ OF平分∠AOD,∴∠AOF=∠DOF.又∠AOC=∠BOD,∴ ∠AOF + ∠AOC = ∠DOF +∠BOD,即∠COF=∠BOF.
(2)解:∠AOD=180°--∠BOD=180°-24°=156°,
又OE⊥AB,∴∠AOE=90°,∴ ∠EOF =∠AOE - ∠AOF =90°-78°=12°.
21. 解:(1)根据题意,得3×(--1) +5=2;--1+3×5=14,∴若点P 的坐标为( --1,5),则它的“3 级关联点”的坐标为(2,14). 故答案为:(2,14).
(2)设点P的坐标为(a,b),由题意可得 解得 点 P的坐标为(2,-1).
(3)由题意得点 的“-3级关联点”为
①当点 位于x轴上时, 解得 m =
②当点 位于y轴上时, 解得 m= 3, 。
综上所述,点 的坐标为 或
22. 解:(1)如图 1,作 EF∥AB,∵ BE 平分. DE 平分
(2)如图2,作EF∥AB,∵BE平分 DE平分
)
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 下列几组图形中,通过平移后能够重合的是 ( )
2. 若-3是m的一个平方根,则m+40的算术平方根是 ( )
A.7 B. -7 C. ±7 D.49
3. 如图是象棋残局,已知棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为 ( )
A.(-3,3) B.(3,2) C.(1,3) D.(0,3)
4. 如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有 ( )
①线段CD的长度是C点到AB的距离;②线段AC是A点到BC的距离;③AB>AC>CD.
A.0个 B.1个 C.2个 D.3个
5. 下列命题中,是真命题的是 ( )
A. -1的平方根是1 B.5是25的一个平方根
C.(-4) 的平方根是-4 D.64的立方根是±4
6. 在平面直角坐标系中,将点(-2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为 ( )
A.(2,5) B.(-6,5) C.(2,1) D.(-6,1)
7. 如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=43°,那么∠2的度数是 ( )
A.48° B.107° C.92°
8. 已知x,y为正整数,且 则y 的最小值为 ( )
A.1 B.3 C.4 D.9
9. 在平面直角坐标系xOy中,对于点 P(x,y),我们把 叫做点 P 的友好点.已知点A 的友好点为A ,点A 的友好点为A ,点A 的友好点为 ,这样依次得到各点.若点 的坐标为(-3,2),设A (x,y),则x+y的值是 ( )
A. - 5 B. - 1 C.3 D.5
10. 如图,AD∥BC,∠D=∠ABC,点 E 是边 DC上一点,连接AE交BC的延长线于点 H,点F 是边 AB 上一点,使得 作∠FEH的平分线EG交BH于点G,若∠DEH=100°,则. 的度数为( )
A.30° B.40° C.50°
二、填空题(每小题4分,共24分)
的平方根是 , = .
12. 如果将点A(-3,-2)向右平移2个单位长度,再向上平移3个单位长度得到点 B,那么点B在第 象限.
13. 如图,直线 EF,CD 相交于点 O,OA⊥OB,OD 平分∠AOF,若. 则 = .
14. 实数a,b,c在数轴上的位置如图所示,则c-a-b 0(填“>”“<”或“=”).
15. 如图,直线AB∥CD,∠A=60°,∠D=40°,则∠E= .
16. 在平面直角坐标系中有一点P(a+1,a-3),其中a为任意实数,m,n分别表示点 P到x轴和y轴的距离,则m+n的最小值为 .
三、解答题(共56分)
17. (8分)求下列x的值:
18. (6分)定义如下的运算“ ”:对于任意实数a,b,都有 例如: 是 否存在负整数x,使得3 x的值小于4 若存在,求出所有的x;若不存在,请说明理由.
19. (8分)如图,在平面直角坐标系中,图中的网格是由边长相等的小正方形组成的,点A,B,C的坐标分别为
(1)请写出点D,E,F,G的坐标.
(2)求图中阴影部分(多边形ABCDEFG)的面积.
20. (10分)如图,直线AB,CD 相交于点O,过点O作 且OF平分.
(1)求证:
(2)求 的度数.
21. (12分)在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ ay),则称点Q是点P的“a级关联点”(其中a为常数,且a≠0),例如,点P(1,4)的“2级关联点”为Q(2×1+4,1+2×4),即Q(6,9).
(1)若点 P 的坐标为( -1,5),则它的“3级关联点”的坐标为 .
(2)若点 P 的“5级关联点”的坐标为(9,-3),求点 P 的坐标.
(3)若点P(m-1,2m)的“-3级关联点” P'位于坐标轴上,求点 P'的坐标.
22. (12分)如图1,AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE,DE所在直线交于点 E,∠ADC=80°.
(1)若∠ABC=50°,求∠BED 的度数.
(2)将线段BC沿DC方向平移,使得点B 在点A 的右侧,其他条件不变,若∠ABC=120°,求∠BED 的度数.
专项训练卷(一)
1. C 2. A 3. C 4. C 5. B 6. C 7. B 8. B 9. C 10. B11. ± -3 12. 二 13.36° 14. > 15.20° 16.4
17. 解:( 移项,得 开平方,得x--2=4或x-2=-4,解得x=6或x=-2.
开立方,得2x--1 = - 9,移项、合并得2x=-8,解得x= - 4.
18. 解:存在. 理由如下:
∵3 x=-3(3+x)+1=-8-3x;由题意-8-3x<4,解得x>-4.∴满足条件的负整数有-3,-2,--1.
19. 解:(1)点D,E,F,G的坐标分别为:(0,-2),(5,-3),(3,4),(-1,2).
(2)阴影部分(多边形ABCDEFG)的面积为:
70-5-7-8-3.5=46.5
20. (1)证明:∵ OF平分∠AOD,∴∠AOF=∠DOF.又∠AOC=∠BOD,∴ ∠AOF + ∠AOC = ∠DOF +∠BOD,即∠COF=∠BOF.
(2)解:∠AOD=180°--∠BOD=180°-24°=156°,
又OE⊥AB,∴∠AOE=90°,∴ ∠EOF =∠AOE - ∠AOF =90°-78°=12°.
21. 解:(1)根据题意,得3×(--1) +5=2;--1+3×5=14,∴若点P 的坐标为( --1,5),则它的“3 级关联点”的坐标为(2,14). 故答案为:(2,14).
(2)设点P的坐标为(a,b),由题意可得 解得 点 P的坐标为(2,-1).
(3)由题意得点 的“-3级关联点”为
①当点 位于x轴上时, 解得 m =
②当点 位于y轴上时, 解得 m= 3, 。
综上所述,点 的坐标为 或
22. 解:(1)如图 1,作 EF∥AB,∵ BE 平分. DE 平分
(2)如图2,作EF∥AB,∵BE平分 DE平分
)
同课章节目录
