广东省汕头市潮南区井都中学人教版数学七年级下册 期末综合测试卷(含答案)
文档属性
| 名称 | 广东省汕头市潮南区井都中学人教版数学七年级下册 期末综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 476.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 11:10:02 | ||
图片预览




文档简介
期末综合测试卷
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 在下列各数 ,3.1415926,0.23,, ,0.2020020002……(每两个2之间依次多1个0)中,无理数的个数有 ( )
A.1个 B.2个 C.3个 D.4个
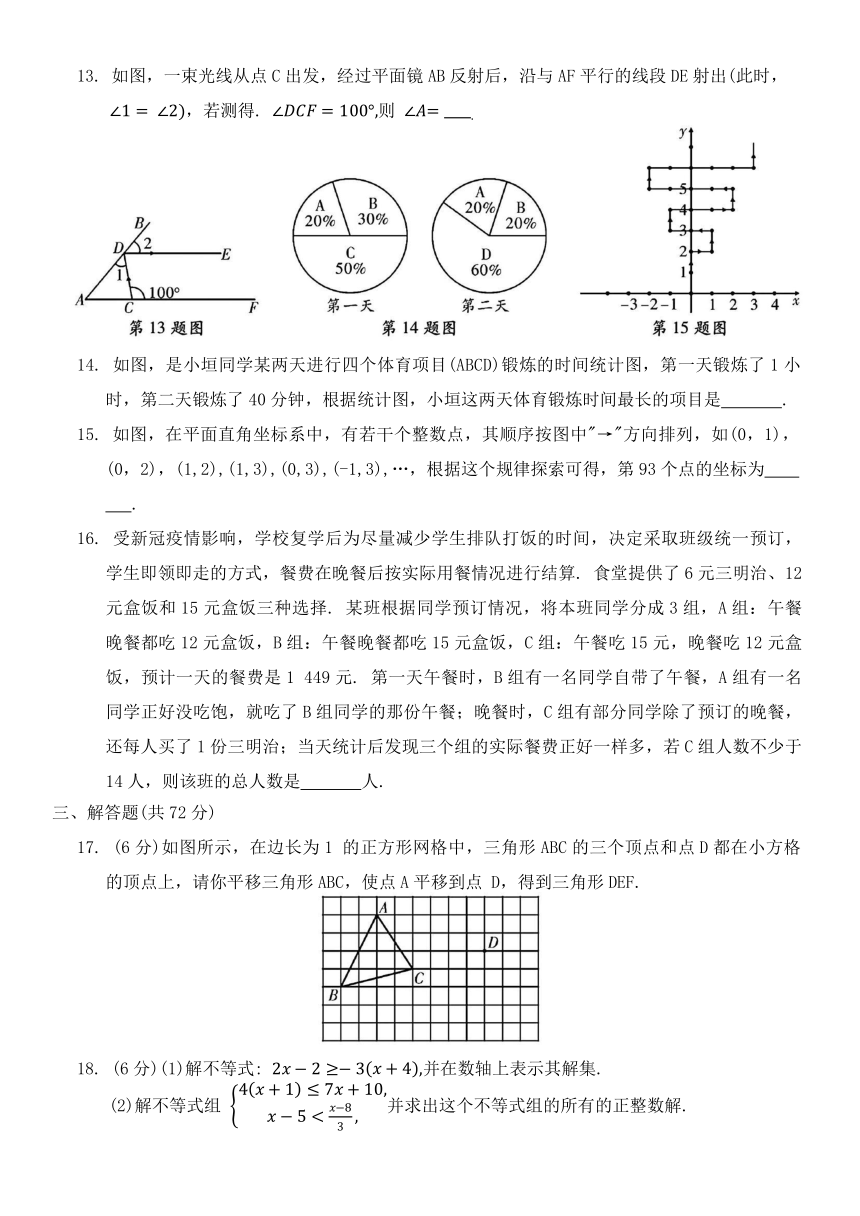
2. 为了保障艺术节表演的整体效果,某校在操场中标记了几个关键位置,如图是利用平面坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示点A的坐标为(1,0),表示点 B的坐标为(3,3),则表示其他位置的点的坐标正确的是( )
A. C(-1,0) B. D(-3,1) C. E( - 1,-5) D. F(5,-1)
3. 如图,由下列已知条件推出的结论中,正确的是 ( )
A. 由∠1=∠5,可以推出AD∥BC
B. 由∠2=∠6,可以推出AD∥BC
C. 由∠1+∠4=90°,可以推出AB∥CD
D. 由∠ABC+∠BCD=180°,可以推出AD∥BC
4. 如图,AB⊥BC,∠ABD的度数比∠DBC的度数多15°,设∠ABD和∠DBC的度数分别为x°,y°,根据题意,下列方程正确的是 ( )
5. 如图,按下面的程序进行运算. 规定:程序运行到“判断结果是否大于28”为一次运算. 若运算进行了3次才停止,则x的取值范围是 ( )
A.26. 某校七年级开展"阳光体育"活动,对爱好乒乓球、足球、篮球、羽毛球的学生人数进行统计,得到如图所示的扇形统计图. 若爱好羽毛球的人数是爱好足球的人数的4倍,爱好乒乓球的人数是21人,则下列正确的是 ( )
A. 被调查的学生人数为80人
B. 喜欢篮球的人数为16人
C. 喜欢羽毛球的人数为30人
D. 喜欢足球的扇形的圆心角为36°
7. 如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为 ( )
A.(1,3) B.(5,1) C.(1,3)或(3,5) D.(1,3)或(5,1)
8. 去年某市空气质量良好(二级以上)的天数与全年天数(365天)之比达到64%,如果明年(365天)这样的比值要超过80%,那么明年空气质量良好的天数比去年至少要增加的天数为 ( )
A.58 B.59 C.60 D.61
9. 如图所示,现有如图(1)的小长方形纸片若干块,已知小长方形的长为a,宽为b.用3个如图(2)的全等图形和8个如图(1)的小长方形,拼成如图(3)的大长方形,若大长方形的宽为30 cm,则图(3)中阴影部分面积与整个图形的面积之比为 ( )
A. B. C. D.
10. 已知AB∥CD,点E,F分别在直线AB,CD上,点P在AB,CD之间且在 EF 的左侧,若将射线EA沿EP折叠,射线FC沿FP 折叠,折叠后的两条射线互相垂直,则∠EPF 的度数为 ( )
A.120° B.135° C.45°或135° D.60°或120°
二、填空题(每小题3分,共18分)
11. 不等式 的解为 .
12. 若 则a-b+c= .
13. 如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时, ,若测得. 则
14. 如图,是小垣同学某两天进行四个体育项目(ABCD)锻炼的时间统计图,第一天锻炼了1小时,第二天锻炼了40分钟,根据统计图,小垣这两天体育锻炼时间最长的项目是 .
15. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中"→"方向排列,如(0,1),(0,2),(1,2),(1,3),(0,3),(-1,3),…,根据这个规律探索可得,第93个点的坐标为 .
16. 受新冠疫情影响,学校复学后为尽量减少学生排队打饭的时间,决定采取班级统一预订,学生即领即走的方式,餐费在晚餐后按实际用餐情况进行结算. 食堂提供了6元三明治、12元盒饭和15元盒饭三种选择. 某班根据同学预订情况,将本班同学分成3组,A组:午餐晚餐都吃12元盒饭,B组:午餐晚餐都吃15元盒饭,C组:午餐吃15元,晚餐吃12元盒饭,预计一天的餐费是1 449元. 第一天午餐时,B组有一名同学自带了午餐,A组有一名同学正好没吃饱,就吃了B组同学的那份午餐;晚餐时,C组有部分同学除了预订的晚餐,还每人买了1份三明治;当天统计后发现三个组的实际餐费正好一样多,若C组人数不少于14人,则该班的总人数是 人.
三、解答题(共72分)
17. (6分)如图所示,在边长为1 的正方形网格中,三角形ABC的三个顶点和点D都在小方格的顶点上,请你平移三角形ABC,使点A平移到点 D,得到三角形DEF.
18. (6分)(1)解不等式: 并在数轴上表示其解集.
(2)解不等式组 并求出这个不等式组的所有的正整数解.
19. (6分)某高速公路规定行驶汽车的速度不得超过100 km/h,当发生交通事故时,交通警察通常根据刹车后车轮滑过的距离估计车辆的行驶速度,所用的检验公式是 其中v(km/h)表示车速,d(m)表示刹车后车轮滑过的距离,f表示摩擦系数.在一次交通事故中,经测量 ,请你判断一下,肇事汽车当时是否超出了规定的速度
20. (6分)为了取得扶贫工作的胜利,某市对扶贫工作人员进行了扶贫知识的培训与测试,随机抽取了部分人员的测试成绩作为样本,并将成绩划分为A,B,C,D四个不同的等级,绘制成不完整统计图如图,请根据图中的信息,解答下列问题:
(1)样本容量为 .
(2)补全条形统计图,并填空:
(3)若全市有10 000人参加了本次测试,估计本次测试成绩为A级的人数为多少
21. (6分)已知点 P(3a-15,2-a).
(1)若点P到x轴的距离是 试求出a的值.
(2)在(1)的条件下,点Q 如果是点 P向上平移3个单位长度得到的,试求出点Q 的坐标.
(3)若点 P 位于第三象限且横、纵坐标都是整数,试求点 P 的坐标.
22. (6分)(1)在关于x,y的二元一次方程组 中,x>1,y<0,求a的取值范围.
(2)已知x-2y=4,且x>8,y<4,求3x+2y的取值范围.
(3)已知a-b=m,在关于x,y的二元一次方程组 中,x<0,y>0,化简2la+b-3+ ml+3|m-4+a+ bl.
23. (8分)将一副三角板中的两块直角三角尺的直角顶点O 按如图方式叠放在一起.
(1)如图①,若∠BOD=35°,则∠AOC= ;若∠AOC=135°,则∠BOD= .(直接写出结论即可)
(2)如图②,若∠AOC=140°,则∠BOD= .(直接写出结论即可)
(3)猜想∠AOC与∠BOD 的大小关系,并结合图①说明理由.
(4)三角尺AOB不动,将三角尺COD的OD 边与OA 边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当. )等于多少度时,这两块三角尺各有一条边互相垂直,直接写出 角度所有可能的值,不用说明理由.
24. (9分)某制纸厂生产A型,B型两种不同规格的纸,需用甲、乙两种不同的原料. 若甲原料成本为0.5元,乙原料成本为1元/ kg,其他相关数据如下表所示:
甲原料/m 乙原料/ kg 售价/元
每百张A型纸 1 2 4
每百张B型纸 1.2 3 5
(1)若生产这两种纸需用甲原料 、乙原料240 kg,则能生产这两种规格的纸各多少百张
(2)若该厂生产A型纸a百张,则生产a百张这种 A 型纸的利润是多少元(用含a的式子表示) (利润=售价-成本)
(3)该厂发现,当制纸总量超过10 000百张时,需额外支出8 800 元的设备维护费,现该厂接到一笔订单,要求生产A 型纸的数量是B型纸数量的2倍,若该厂希望获得13 200 元的利润,则有哪几种生产方案
25. (9分)小龙在学校组织的社会调查活动中负责了解他所居住的小区452户居民的家庭收入情况,他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图.
分组 频数 百分比
600≤x<800 2 5%
800≤x<1 000 6 15%
1 000≤x<1 200 ——— 45%
——— 9 22.5%
——— ——
1 600≤x<1 800 2
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)请你估计该居民小区家庭属于中等收入(大于1000 不足1600元)的大约有多少户
26. (10分)在平面直角坐标系中, ,直角三角形ABC 的边与x轴分别相交于O,G两点,与直线DM分别交于E,F两点,
(1)将直角三角形ABC如图1位置摆放,如果 则
(2)将直角三角形 ABC 如图2位置摆放,N 为AC 上一点, ,请写出 与 之间的关系,并说明理由.
(3)将直角三角形ABC 如图3位置摆放,若 ,延长AC交DM于点 Q,点 P 是射线 GF 上一动点,探究 与 的数量关系,请直接写出结论.(题中的所有角都大于 小于
期末综合测试卷
1. C 2. D 3. B 4. D 5. A 6. D 7. D 8. B9. B 10. C16. x<1 12.6 13.50° 14. C 15.( -5,14) 16.54
17. 解:如图所示:
18. 解: ,
在数轴上表示不等式的解集为:
解不等式①得 ,解不等式
②得 ∴不等式组的解集为 ∴不等式组的所有的正整数解为:1,2,3.
19. 解:将d=32,f=2代入 得 128(km/h).
∵128>100,∴肇事汽车当时的速度超出了规定的速度.
20. 解:(1)样本容量为:1 ,故答案为:60.
(2)C等级的学生有: (人),
补全条形统计图如图所示, ,故答案为:10.
(人),答:本次测试成绩为 A 级的人数为4 000人.
21. 解:(1)∵点 解得 或
(2)当 时点
当 时,点
∴点Q的坐标为 或
(3)∵点P(3a--15,2--a)位于第三象限,解得222. 解:(1)解方程组 ←
解得0(2)设 ,联立得方程组 解得
解得 ∴28<3x+2y<44.
(3)解方程组 得
解得1.523. 解:(1)若∠BOD=35°,∵∠AOB =∠COD =90°,
∴ ∠AOC=∠AOB +∠COD - ∠BOD =90°+90°-35°= 145°.
若∠AOC=135°,则∠BOD=∠AOB+∠COD-∠AOC=90°+90°-135°=45°.故答案为:145°;45°.
(2)若∠AOC=140°,则∠BOD =360°-∠AOC-∠AOB -∠COD=360°-140°-90°-90°=40°. 故答案为:40°.
(3)∠AOC与∠BOD互补. 理由如下:∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵ ∠AOD+∠BOD + ∠BOC = ∠AOC,∴ ∠AOC + ∠BOD = 180°,∴∠AOC与∠BOD互补.
(4)当OD⊥AB时,∠AOD=30°,当CD⊥OB 时,∠AOD =45°,当CD⊥AB时,∠AOD=75°,
当OC⊥AB 时,∠AOD =60°,当CD⊥OA时,∠AOD=45°,
综上所述,∠AOD 角度可能为30°,45°,60°,75°.
24. 解:(1)设生产 A 型纸x百张,B 型纸y百张,由题意得 解得
答:生产A 型纸60百张,B型纸40 百张.
(2)4a-(0.5×a×1+1×a×2)=1.5a,
答:生产a百张这种A 型纸的利润是1.5a元.
(3)设生产B型纸m百张,则生产A 型纸2m 百张,则2m百张A 型纸的利润为1.5×2m=3m,,m百张B型纸的利润为5 ,①当m+2m<10000时,有3m+1.4m=13 200,解得m=3000,则2m=6000,即生产A型纸6000百张,则生产B型纸3000百张.②当m+2m>10000时,3m+1.4m=13 200+8 800,解得m=5000,则2m=10000,即生产A型纸10000百张,生产B型纸5 000 百张;因此有两种生产方案,生产 A 型纸6000百张,B型纸3 000百张或生产A 型纸 10 000 百张,B型纸5 000 百张.
25. 解: 的频数为
的频数为 其对应百分比为 对应的百分比为 补全频数分布表如下:
分组 频数 百分比
600≤x<800 2 5%
800≤x<1 000 6 15%
l 000≤x<1 200 18 45%
1 200≤x<1 400 9 22.5%
1 400≤x<1 600 3 7.5%
1 600≤x<1 800 2 5%
合计 40 100%
(2)补全频数分布直方图如下:
(3)估计该居民小区家庭属于中等收入(大于1 000 不足1 600元)的大约有
339(户).
26. 解:(1)如图1,作CP∥x轴,
∵D(0,-3),M(4,-3),∴DM∥x轴,∴CP∥DM∥x轴,
∴ ∠AOG = ∠1,∠2 + ∠CEF = 180°,∴ ∠2 = 180° -∠CEF.∵∠1+∠2=90°,∴∠AOG+180°-∠CEF=90°.
∵∠AOG=46°,∴∠CEF=136°.故答案为:136°.
(2)∠AOG+∠NEF=90°. 理由如下:如图2,作CP∥x轴,
∴CP∥DM∥x轴,∴∠AOG=∠1,∠2+∠CEF = 180°. ∵ ∠NED + ∠CEF =180°,∴ ∠2 = ∠NED. ∵ ∠1 + ∠2 =90°,∴ ∠AOG+∠NEF=90°.
(3)如图3,当点 P 在线段GF 上时,过点P作PN∥OG,
∴NP∥OG∥DM,∴ ∠GOP =∠NPO,∠PQF=∠NPQ,∴ ∠OPQ =∠OPN+∠NPQ=∠GOP+∠PQF,∴∠OPQ =140°-∠POQ+∠PQF;
如图4,当点 P 在线段GF 的延长线上时,过点 P作PN∥OG,
∴NP∥OG∥DM,∴∠GOP =∠OPN,∠PQF = ∠NPQ,∵ ∠OPN = ∠OPQ+ ∠QPN, ∴ ∠GOP = ∠OPQ +∠PQF,∴ 140° - ∠POQ = ∠OPQ+∠PQF.
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 在下列各数 ,3.1415926,0.23,, ,0.2020020002……(每两个2之间依次多1个0)中,无理数的个数有 ( )
A.1个 B.2个 C.3个 D.4个
2. 为了保障艺术节表演的整体效果,某校在操场中标记了几个关键位置,如图是利用平面坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示点A的坐标为(1,0),表示点 B的坐标为(3,3),则表示其他位置的点的坐标正确的是( )
A. C(-1,0) B. D(-3,1) C. E( - 1,-5) D. F(5,-1)
3. 如图,由下列已知条件推出的结论中,正确的是 ( )
A. 由∠1=∠5,可以推出AD∥BC
B. 由∠2=∠6,可以推出AD∥BC
C. 由∠1+∠4=90°,可以推出AB∥CD
D. 由∠ABC+∠BCD=180°,可以推出AD∥BC
4. 如图,AB⊥BC,∠ABD的度数比∠DBC的度数多15°,设∠ABD和∠DBC的度数分别为x°,y°,根据题意,下列方程正确的是 ( )
5. 如图,按下面的程序进行运算. 规定:程序运行到“判断结果是否大于28”为一次运算. 若运算进行了3次才停止,则x的取值范围是 ( )
A.2
A. 被调查的学生人数为80人
B. 喜欢篮球的人数为16人
C. 喜欢羽毛球的人数为30人
D. 喜欢足球的扇形的圆心角为36°
7. 如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为 ( )
A.(1,3) B.(5,1) C.(1,3)或(3,5) D.(1,3)或(5,1)
8. 去年某市空气质量良好(二级以上)的天数与全年天数(365天)之比达到64%,如果明年(365天)这样的比值要超过80%,那么明年空气质量良好的天数比去年至少要增加的天数为 ( )
A.58 B.59 C.60 D.61
9. 如图所示,现有如图(1)的小长方形纸片若干块,已知小长方形的长为a,宽为b.用3个如图(2)的全等图形和8个如图(1)的小长方形,拼成如图(3)的大长方形,若大长方形的宽为30 cm,则图(3)中阴影部分面积与整个图形的面积之比为 ( )
A. B. C. D.
10. 已知AB∥CD,点E,F分别在直线AB,CD上,点P在AB,CD之间且在 EF 的左侧,若将射线EA沿EP折叠,射线FC沿FP 折叠,折叠后的两条射线互相垂直,则∠EPF 的度数为 ( )
A.120° B.135° C.45°或135° D.60°或120°
二、填空题(每小题3分,共18分)
11. 不等式 的解为 .
12. 若 则a-b+c= .
13. 如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时, ,若测得. 则
14. 如图,是小垣同学某两天进行四个体育项目(ABCD)锻炼的时间统计图,第一天锻炼了1小时,第二天锻炼了40分钟,根据统计图,小垣这两天体育锻炼时间最长的项目是 .
15. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中"→"方向排列,如(0,1),(0,2),(1,2),(1,3),(0,3),(-1,3),…,根据这个规律探索可得,第93个点的坐标为 .
16. 受新冠疫情影响,学校复学后为尽量减少学生排队打饭的时间,决定采取班级统一预订,学生即领即走的方式,餐费在晚餐后按实际用餐情况进行结算. 食堂提供了6元三明治、12元盒饭和15元盒饭三种选择. 某班根据同学预订情况,将本班同学分成3组,A组:午餐晚餐都吃12元盒饭,B组:午餐晚餐都吃15元盒饭,C组:午餐吃15元,晚餐吃12元盒饭,预计一天的餐费是1 449元. 第一天午餐时,B组有一名同学自带了午餐,A组有一名同学正好没吃饱,就吃了B组同学的那份午餐;晚餐时,C组有部分同学除了预订的晚餐,还每人买了1份三明治;当天统计后发现三个组的实际餐费正好一样多,若C组人数不少于14人,则该班的总人数是 人.
三、解答题(共72分)
17. (6分)如图所示,在边长为1 的正方形网格中,三角形ABC的三个顶点和点D都在小方格的顶点上,请你平移三角形ABC,使点A平移到点 D,得到三角形DEF.
18. (6分)(1)解不等式: 并在数轴上表示其解集.
(2)解不等式组 并求出这个不等式组的所有的正整数解.
19. (6分)某高速公路规定行驶汽车的速度不得超过100 km/h,当发生交通事故时,交通警察通常根据刹车后车轮滑过的距离估计车辆的行驶速度,所用的检验公式是 其中v(km/h)表示车速,d(m)表示刹车后车轮滑过的距离,f表示摩擦系数.在一次交通事故中,经测量 ,请你判断一下,肇事汽车当时是否超出了规定的速度
20. (6分)为了取得扶贫工作的胜利,某市对扶贫工作人员进行了扶贫知识的培训与测试,随机抽取了部分人员的测试成绩作为样本,并将成绩划分为A,B,C,D四个不同的等级,绘制成不完整统计图如图,请根据图中的信息,解答下列问题:
(1)样本容量为 .
(2)补全条形统计图,并填空:
(3)若全市有10 000人参加了本次测试,估计本次测试成绩为A级的人数为多少
21. (6分)已知点 P(3a-15,2-a).
(1)若点P到x轴的距离是 试求出a的值.
(2)在(1)的条件下,点Q 如果是点 P向上平移3个单位长度得到的,试求出点Q 的坐标.
(3)若点 P 位于第三象限且横、纵坐标都是整数,试求点 P 的坐标.
22. (6分)(1)在关于x,y的二元一次方程组 中,x>1,y<0,求a的取值范围.
(2)已知x-2y=4,且x>8,y<4,求3x+2y的取值范围.
(3)已知a-b=m,在关于x,y的二元一次方程组 中,x<0,y>0,化简2la+b-3+ ml+3|m-4+a+ bl.
23. (8分)将一副三角板中的两块直角三角尺的直角顶点O 按如图方式叠放在一起.
(1)如图①,若∠BOD=35°,则∠AOC= ;若∠AOC=135°,则∠BOD= .(直接写出结论即可)
(2)如图②,若∠AOC=140°,则∠BOD= .(直接写出结论即可)
(3)猜想∠AOC与∠BOD 的大小关系,并结合图①说明理由.
(4)三角尺AOB不动,将三角尺COD的OD 边与OA 边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当. )等于多少度时,这两块三角尺各有一条边互相垂直,直接写出 角度所有可能的值,不用说明理由.
24. (9分)某制纸厂生产A型,B型两种不同规格的纸,需用甲、乙两种不同的原料. 若甲原料成本为0.5元,乙原料成本为1元/ kg,其他相关数据如下表所示:
甲原料/m 乙原料/ kg 售价/元
每百张A型纸 1 2 4
每百张B型纸 1.2 3 5
(1)若生产这两种纸需用甲原料 、乙原料240 kg,则能生产这两种规格的纸各多少百张
(2)若该厂生产A型纸a百张,则生产a百张这种 A 型纸的利润是多少元(用含a的式子表示) (利润=售价-成本)
(3)该厂发现,当制纸总量超过10 000百张时,需额外支出8 800 元的设备维护费,现该厂接到一笔订单,要求生产A 型纸的数量是B型纸数量的2倍,若该厂希望获得13 200 元的利润,则有哪几种生产方案
25. (9分)小龙在学校组织的社会调查活动中负责了解他所居住的小区452户居民的家庭收入情况,他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图.
分组 频数 百分比
600≤x<800 2 5%
800≤x<1 000 6 15%
1 000≤x<1 200 ——— 45%
——— 9 22.5%
——— ——
1 600≤x<1 800 2
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)请你估计该居民小区家庭属于中等收入(大于1000 不足1600元)的大约有多少户
26. (10分)在平面直角坐标系中, ,直角三角形ABC 的边与x轴分别相交于O,G两点,与直线DM分别交于E,F两点,
(1)将直角三角形ABC如图1位置摆放,如果 则
(2)将直角三角形 ABC 如图2位置摆放,N 为AC 上一点, ,请写出 与 之间的关系,并说明理由.
(3)将直角三角形ABC 如图3位置摆放,若 ,延长AC交DM于点 Q,点 P 是射线 GF 上一动点,探究 与 的数量关系,请直接写出结论.(题中的所有角都大于 小于
期末综合测试卷
1. C 2. D 3. B 4. D 5. A 6. D 7. D 8. B9. B 10. C16. x<1 12.6 13.50° 14. C 15.( -5,14) 16.54
17. 解:如图所示:
18. 解: ,
在数轴上表示不等式的解集为:
解不等式①得 ,解不等式
②得 ∴不等式组的解集为 ∴不等式组的所有的正整数解为:1,2,3.
19. 解:将d=32,f=2代入 得 128(km/h).
∵128>100,∴肇事汽车当时的速度超出了规定的速度.
20. 解:(1)样本容量为:1 ,故答案为:60.
(2)C等级的学生有: (人),
补全条形统计图如图所示, ,故答案为:10.
(人),答:本次测试成绩为 A 级的人数为4 000人.
21. 解:(1)∵点 解得 或
(2)当 时点
当 时,点
∴点Q的坐标为 或
(3)∵点P(3a--15,2--a)位于第三象限,解得2
解得0
解得 ∴28<3x+2y<44.
(3)解方程组 得
解得1.5
∴ ∠AOC=∠AOB +∠COD - ∠BOD =90°+90°-35°= 145°.
若∠AOC=135°,则∠BOD=∠AOB+∠COD-∠AOC=90°+90°-135°=45°.故答案为:145°;45°.
(2)若∠AOC=140°,则∠BOD =360°-∠AOC-∠AOB -∠COD=360°-140°-90°-90°=40°. 故答案为:40°.
(3)∠AOC与∠BOD互补. 理由如下:∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵ ∠AOD+∠BOD + ∠BOC = ∠AOC,∴ ∠AOC + ∠BOD = 180°,∴∠AOC与∠BOD互补.
(4)当OD⊥AB时,∠AOD=30°,当CD⊥OB 时,∠AOD =45°,当CD⊥AB时,∠AOD=75°,
当OC⊥AB 时,∠AOD =60°,当CD⊥OA时,∠AOD=45°,
综上所述,∠AOD 角度可能为30°,45°,60°,75°.
24. 解:(1)设生产 A 型纸x百张,B 型纸y百张,由题意得 解得
答:生产A 型纸60百张,B型纸40 百张.
(2)4a-(0.5×a×1+1×a×2)=1.5a,
答:生产a百张这种A 型纸的利润是1.5a元.
(3)设生产B型纸m百张,则生产A 型纸2m 百张,则2m百张A 型纸的利润为1.5×2m=3m,,m百张B型纸的利润为5 ,①当m+2m<10000时,有3m+1.4m=13 200,解得m=3000,则2m=6000,即生产A型纸6000百张,则生产B型纸3000百张.②当m+2m>10000时,3m+1.4m=13 200+8 800,解得m=5000,则2m=10000,即生产A型纸10000百张,生产B型纸5 000 百张;因此有两种生产方案,生产 A 型纸6000百张,B型纸3 000百张或生产A 型纸 10 000 百张,B型纸5 000 百张.
25. 解: 的频数为
的频数为 其对应百分比为 对应的百分比为 补全频数分布表如下:
分组 频数 百分比
600≤x<800 2 5%
800≤x<1 000 6 15%
l 000≤x<1 200 18 45%
1 200≤x<1 400 9 22.5%
1 400≤x<1 600 3 7.5%
1 600≤x<1 800 2 5%
合计 40 100%
(2)补全频数分布直方图如下:
(3)估计该居民小区家庭属于中等收入(大于1 000 不足1 600元)的大约有
339(户).
26. 解:(1)如图1,作CP∥x轴,
∵D(0,-3),M(4,-3),∴DM∥x轴,∴CP∥DM∥x轴,
∴ ∠AOG = ∠1,∠2 + ∠CEF = 180°,∴ ∠2 = 180° -∠CEF.∵∠1+∠2=90°,∴∠AOG+180°-∠CEF=90°.
∵∠AOG=46°,∴∠CEF=136°.故答案为:136°.
(2)∠AOG+∠NEF=90°. 理由如下:如图2,作CP∥x轴,
∴CP∥DM∥x轴,∴∠AOG=∠1,∠2+∠CEF = 180°. ∵ ∠NED + ∠CEF =180°,∴ ∠2 = ∠NED. ∵ ∠1 + ∠2 =90°,∴ ∠AOG+∠NEF=90°.
(3)如图3,当点 P 在线段GF 上时,过点P作PN∥OG,
∴NP∥OG∥DM,∴ ∠GOP =∠NPO,∠PQF=∠NPQ,∴ ∠OPQ =∠OPN+∠NPQ=∠GOP+∠PQF,∴∠OPQ =140°-∠POQ+∠PQF;
如图4,当点 P 在线段GF 的延长线上时,过点 P作PN∥OG,
∴NP∥OG∥DM,∴∠GOP =∠OPN,∠PQF = ∠NPQ,∵ ∠OPN = ∠OPQ+ ∠QPN, ∴ ∠GOP = ∠OPQ +∠PQF,∴ 140° - ∠POQ = ∠OPQ+∠PQF.
同课章节目录
