1.2.3直角三角形的性质和判定 课件(共23张PPT)
文档属性
| 名称 | 1.2.3直角三角形的性质和判定 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-04 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第一章 直角三角形
1.2.3直角三角形的性质和判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
掌握直角三角形的判别条件.
熟记一些勾股数.
掌握勾股定理的逆定理的探究方法.
02
新知导入
一个三角形满足什么条件才能是直角三角形
(1)有一个角是直角的三角形是直角三角形
(2)有两个角的和为90°的三角形是直角三角形
(3)如果一个三角形的三边a,b,c满足
那么这个三角形是直角三角形吗?
03
新知探究
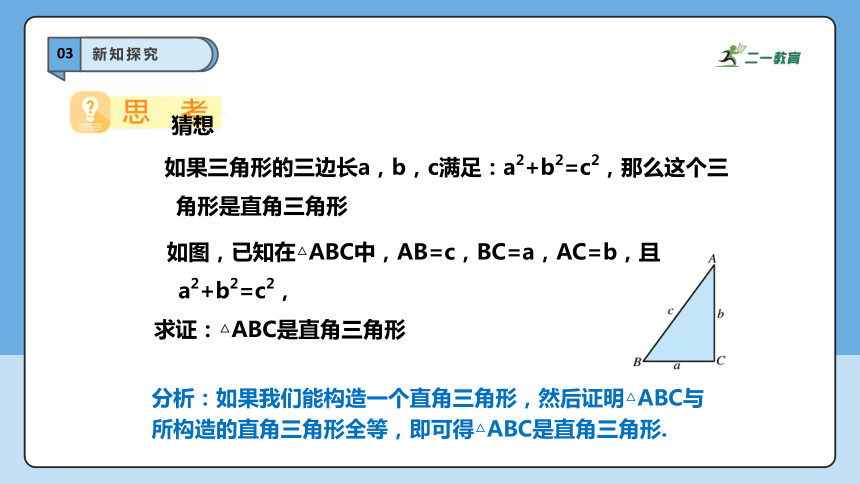
如图,已知在△ABC中,AB=c,BC=a,AC=b,且a2+b2=c2,
求证:△ABC是直角三角形
猜想
如果三角形的三边长a,b,c满足:a2+b2=c2,那么这个三角形是直角三角形
分析:如果我们能构造一个直角三角形,然后证明△ABC与所构造的直角三角形全等,即可得△ABC是直角三角形.
03
新知探究
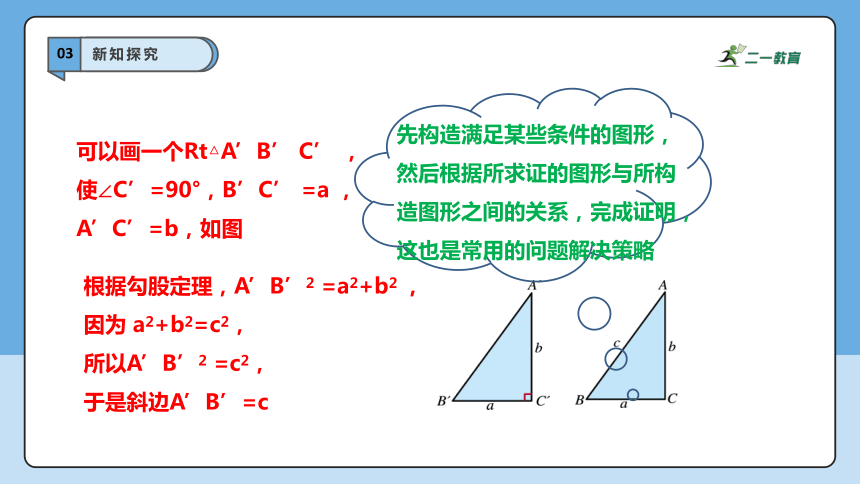
可以画一个Rt△A’B’ C’ ,
使∠C’=90°,B’C’ =a ,
A’C’=b,如图
根据勾股定理,A’B’2 =a2+b2 ,
因为 a2+b2=c2,
所以A’B’2 =c2,
于是斜边A’B’=c
先构造满足某些条件的图形,然后根据所求证的图形与所构造图形之间的关系,完成证明,这也是常用的问题解决策略
03
新知探究
因为BC=B’C’=a,AC=A’C’=b,
AB=A’B’=c
所以△ABC ≌ △A’B’C’(SSS)
于是∠C=∠C’=90° (全等三角形的对应角相等)
所以△ABC是直角三角形.
在△ABC和△A’B’C’中,
03
新知探究
结论
如果三角形的边长a,b,c有下面的关系:
a2 + b2 = c2,那么这个三角形是直角三角形.
直角三角形的判定定理:
C
B
A
c
b
a
注意:(1)这个定理实际就是勾股定理的逆定理。
(2)运用时注意条件。
如图, △ABC的三边为a、b、c,
∵a2 + b2 = c2,
∴ △ABC是直角三角形。
03
新知探究
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
勾股定理
如果三角形的三边长a、b、c满足那么这个三角形是直角三角形。且边C边所对的角为直角.
互逆命题
新课探究
例1
例1 判断由a、b、c 组成的三角形是不是直角三角形:
a=15 , b =8 , c=17
(2) a=13 , b =15 , c=14
满足的三个正整数称为勾股数
根据勾股定理逆定理,判断一个三角形是不是直角三角形,只要看两条较短边长的平方和是否等于最长边的平方。
分析:
(2)∵132+142=169+196=365
而152=225
∴ 132+142≠152
∴这个三角形不是直角三角形
注意:书写格式。
解:(1)∵152+82=225+64=289
而172=289
∴ 152+82=172
∴这个三角形是直角三角形
03
新知讲解
例2
例2 如图,在△ABC中,已知AB=10,BD=6, AC=17,求DC的长.
∠ADC=180°-∠ADB=90°.
即 ADC是直角三角形。
在Rt△ADC中,根据勾股定理,
可得 DC2=AC2-AD2,
解:在△ABD中,
已知 AB = 10,BD=6,AD=8,
根据62+82=102, 即AD2+BD2=AB2.
所以∠ADB = 90°,
所以DC=
04
课堂练习
【知识技能类作业】必做题:
1.满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为1∶2∶3 B.三边长的平方之比为1∶2∶3
C.三边长之比为3∶4∶5 D.三内角之比为3∶4∶5
2.如图,△ABC中,CD⊥AB于D,若AD=2BD,AC=6,BC=3,则BD的长为( )
A.3 B. C.1 D.4
D
A
04
课堂练习
【知识技能类作业】选做题:
3.已知△ABC的三边分别为a,b,c且a=,b=2mn,c=+(m>n,m,n是正整数),△ABC是直角三角形吗?说明理由
∴△ABC是直角三角形
解:∵
04
课堂练习
【综合拓展类作业】
4、如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
04
课堂练习
【综合拓展类作业】
解:连接AC,在Rt△ABC中,
AC2=AB2+BC2=32+42=25,
∴ AC=5.
在△ACD中,∵ AC2+CD2=25+122=169,
而 AB2=132=169,
∴ AC2+CD2=AB2,
∴ ∠ACD=90°.
故S四边形ABCD=S△ABC+S△ACD= AB·BC+AC·CD
=×3×4+ ×5×12=6+30=36.
05
课堂小结
直角三角形的性质与判定
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
勾股定理逆定理:
勾股定理逆定理的运用步骤:
(1)先确定最长边;(2)计算较短的两边的平方和;
(3)若较短两边的平方和等于较长边的平方,则是直角三角形,否则不是直角三角形
06
作业布置
【知识技能类作业】必做题:
1、如图,一电线杆AB的高为10米,当太阳光线与地面的夹角为60°时,其影长AC约为( ≈1.732,结果保留三个有效数字)( )
A.5.00米 B.8.66米 C.17.3米 D.5.77米
2.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为 .
D
120cm2
06
作业布置
【知识技能类作业】选做题:
3.已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD.
求证:△ABC是直角三角形.
证明:∵AC2=AD2+CD2,BC2=CD2+BD2,
∴AC2+BC2=AD2+2CD2+BD2
=AD2+2AD·BD+BD2
=(AD+BD)2=AB2.
∴△ABC是直角三角形.
06
作业布置
【综合拓展类作业】
4、已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.
解:由已知可得a2-10a+25+b2-24b+144+c2-26c+169=0,
配方并化简得,(a-5)2+(b-12)2+(c-13)2=0.
∵(a-5)2≥0,(b-12)2≥0,(c-13)2≥0.
∴a-5=0,b-12=0,c-13=0.
解得a=5,b=12,c=13.
又∵a2+b2=169=c2,
∴△ABC是直角三角形.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.2.3直角三角形的性质和判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
掌握直角三角形的判别条件.
熟记一些勾股数.
掌握勾股定理的逆定理的探究方法.
02
新知导入
一个三角形满足什么条件才能是直角三角形
(1)有一个角是直角的三角形是直角三角形
(2)有两个角的和为90°的三角形是直角三角形
(3)如果一个三角形的三边a,b,c满足
那么这个三角形是直角三角形吗?
03
新知探究
如图,已知在△ABC中,AB=c,BC=a,AC=b,且a2+b2=c2,
求证:△ABC是直角三角形
猜想
如果三角形的三边长a,b,c满足:a2+b2=c2,那么这个三角形是直角三角形
分析:如果我们能构造一个直角三角形,然后证明△ABC与所构造的直角三角形全等,即可得△ABC是直角三角形.
03
新知探究
可以画一个Rt△A’B’ C’ ,
使∠C’=90°,B’C’ =a ,
A’C’=b,如图
根据勾股定理,A’B’2 =a2+b2 ,
因为 a2+b2=c2,
所以A’B’2 =c2,
于是斜边A’B’=c
先构造满足某些条件的图形,然后根据所求证的图形与所构造图形之间的关系,完成证明,这也是常用的问题解决策略
03
新知探究
因为BC=B’C’=a,AC=A’C’=b,
AB=A’B’=c
所以△ABC ≌ △A’B’C’(SSS)
于是∠C=∠C’=90° (全等三角形的对应角相等)
所以△ABC是直角三角形.
在△ABC和△A’B’C’中,
03
新知探究
结论
如果三角形的边长a,b,c有下面的关系:
a2 + b2 = c2,那么这个三角形是直角三角形.
直角三角形的判定定理:
C
B
A
c
b
a
注意:(1)这个定理实际就是勾股定理的逆定理。
(2)运用时注意条件。
如图, △ABC的三边为a、b、c,
∵a2 + b2 = c2,
∴ △ABC是直角三角形。
03
新知探究
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
勾股定理
如果三角形的三边长a、b、c满足那么这个三角形是直角三角形。且边C边所对的角为直角.
互逆命题
新课探究
例1
例1 判断由a、b、c 组成的三角形是不是直角三角形:
a=15 , b =8 , c=17
(2) a=13 , b =15 , c=14
满足的三个正整数称为勾股数
根据勾股定理逆定理,判断一个三角形是不是直角三角形,只要看两条较短边长的平方和是否等于最长边的平方。
分析:
(2)∵132+142=169+196=365
而152=225
∴ 132+142≠152
∴这个三角形不是直角三角形
注意:书写格式。
解:(1)∵152+82=225+64=289
而172=289
∴ 152+82=172
∴这个三角形是直角三角形
03
新知讲解
例2
例2 如图,在△ABC中,已知AB=10,BD=6, AC=17,求DC的长.
∠ADC=180°-∠ADB=90°.
即 ADC是直角三角形。
在Rt△ADC中,根据勾股定理,
可得 DC2=AC2-AD2,
解:在△ABD中,
已知 AB = 10,BD=6,AD=8,
根据62+82=102, 即AD2+BD2=AB2.
所以∠ADB = 90°,
所以DC=
04
课堂练习
【知识技能类作业】必做题:
1.满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为1∶2∶3 B.三边长的平方之比为1∶2∶3
C.三边长之比为3∶4∶5 D.三内角之比为3∶4∶5
2.如图,△ABC中,CD⊥AB于D,若AD=2BD,AC=6,BC=3,则BD的长为( )
A.3 B. C.1 D.4
D
A
04
课堂练习
【知识技能类作业】选做题:
3.已知△ABC的三边分别为a,b,c且a=,b=2mn,c=+(m>n,m,n是正整数),△ABC是直角三角形吗?说明理由
∴△ABC是直角三角形
解:∵
04
课堂练习
【综合拓展类作业】
4、如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
04
课堂练习
【综合拓展类作业】
解:连接AC,在Rt△ABC中,
AC2=AB2+BC2=32+42=25,
∴ AC=5.
在△ACD中,∵ AC2+CD2=25+122=169,
而 AB2=132=169,
∴ AC2+CD2=AB2,
∴ ∠ACD=90°.
故S四边形ABCD=S△ABC+S△ACD= AB·BC+AC·CD
=×3×4+ ×5×12=6+30=36.
05
课堂小结
直角三角形的性质与判定
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
勾股定理逆定理:
勾股定理逆定理的运用步骤:
(1)先确定最长边;(2)计算较短的两边的平方和;
(3)若较短两边的平方和等于较长边的平方,则是直角三角形,否则不是直角三角形
06
作业布置
【知识技能类作业】必做题:
1、如图,一电线杆AB的高为10米,当太阳光线与地面的夹角为60°时,其影长AC约为( ≈1.732,结果保留三个有效数字)( )
A.5.00米 B.8.66米 C.17.3米 D.5.77米
2.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为 .
D
120cm2
06
作业布置
【知识技能类作业】选做题:
3.已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD.
求证:△ABC是直角三角形.
证明:∵AC2=AD2+CD2,BC2=CD2+BD2,
∴AC2+BC2=AD2+2CD2+BD2
=AD2+2AD·BD+BD2
=(AD+BD)2=AB2.
∴△ABC是直角三角形.
06
作业布置
【综合拓展类作业】
4、已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.
解:由已知可得a2-10a+25+b2-24b+144+c2-26c+169=0,
配方并化简得,(a-5)2+(b-12)2+(c-13)2=0.
∵(a-5)2≥0,(b-12)2≥0,(c-13)2≥0.
∴a-5=0,b-12=0,c-13=0.
解得a=5,b=12,c=13.
又∵a2+b2=169=c2,
∴△ABC是直角三角形.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
