云南省2024—2025学年秋季学期九年级数学期末猜题卷(含答案)
文档属性
| 名称 | 云南省2024—2025学年秋季学期九年级数学期末猜题卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
云南省2024—2025学年秋季学期九年级数学期末猜题卷
(全卷三个大题,共24个小题,共6页;满分100分;考试用时120分钟)
一、选择题(本大题共15小题,每小题只有一个正确选项,每小题2分,共30分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2. 下列说法错误是( )
A. 必然事件的概率为1 B. 心想事成是不可能事件
C. 平分弦(非直径)的直径垂直于弦 D. 三角形的内心到三边的距离相等
3.方程的根是( )
A. B. C. D.无实数根
4.若⊙O的半径为4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
5.某地2018年为做好“精准扶贫”,投入资金1480万元用于异地安置,并规划投入资金逐年增加,2020年在2018年的基础上增加投入资金2000万元.若设从2018年到2020年该地投入异地安置资金的年平均增长率为,则下列方程正确的是( )
A. B.
C. D.
6.关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )
A.k≤﹣ B.k≤﹣且k≠0 C.k≥﹣ D.k≥﹣且k≠0
7.如图,四边形是的内接四边形,若,则的度数为( )
A. B. C. D.
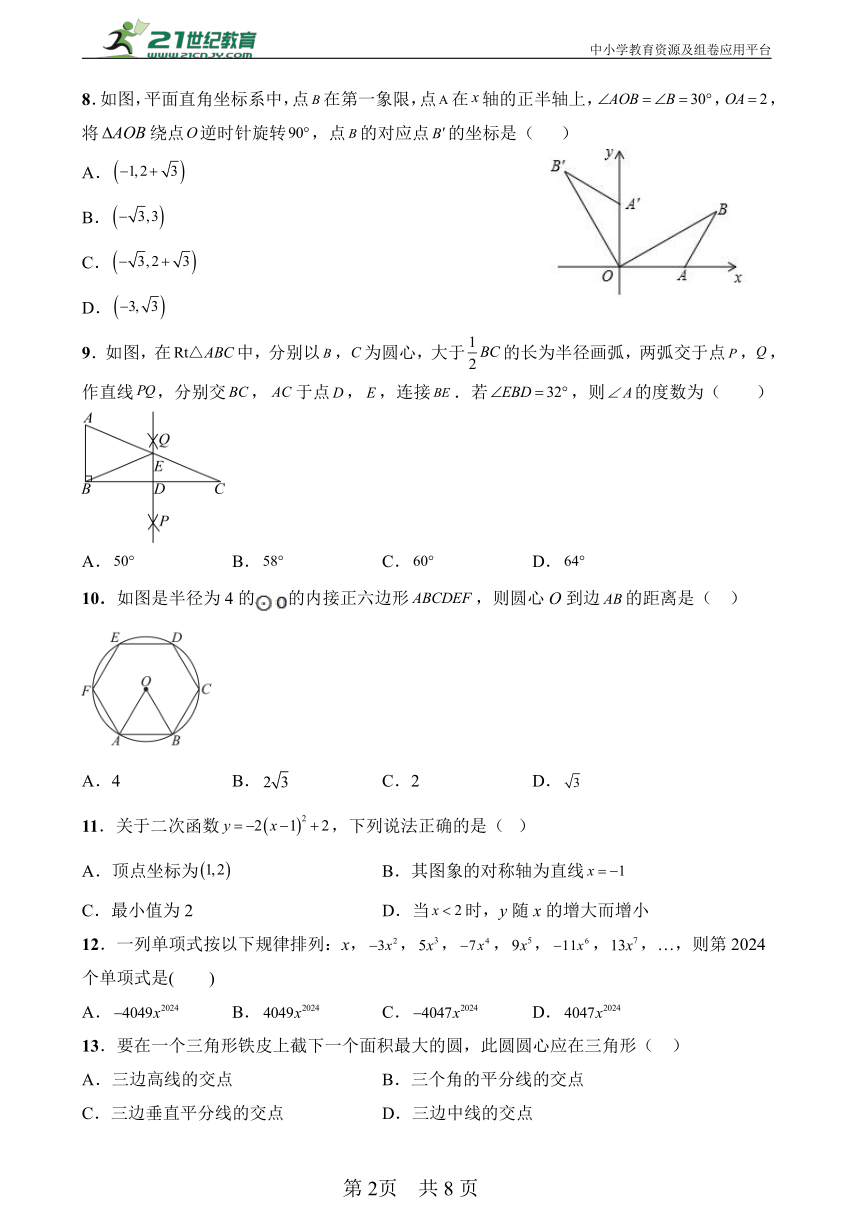
8.如图,平面直角坐标系中,点在第一象限,点在轴的正半轴上,,,将绕点逆时针旋转,点的对应点的坐标是( )
A.
B.
C.
D.
9.如图,在中,分别以,为圆心,大于的长为半径画弧,两弧交于点,,作直线,分别交,于点,,连接.若,则的度数为( )
A. B. C. D.
10.如图是半径为4的的内接正六边形,则圆心O到边的距离是( )
A.4 B. C.2 D.
11.关于二次函数,下列说法正确的是( )
A.顶点坐标为 B.其图象的对称轴为直线
C.最小值为2 D.当时,y随x的增大而增小
12.一列单项式按以下规律排列:x,,,,,,,…,则第2024个单项式是( )
A. B. C. D.
13.要在一个三角形铁皮上截下一个面积最大的圆,此圆圆心应在三角形( )
A.三边高线的交点 B.三个角的平分线的交点
C.三边垂直平分线的交点 D.三边中线的交点
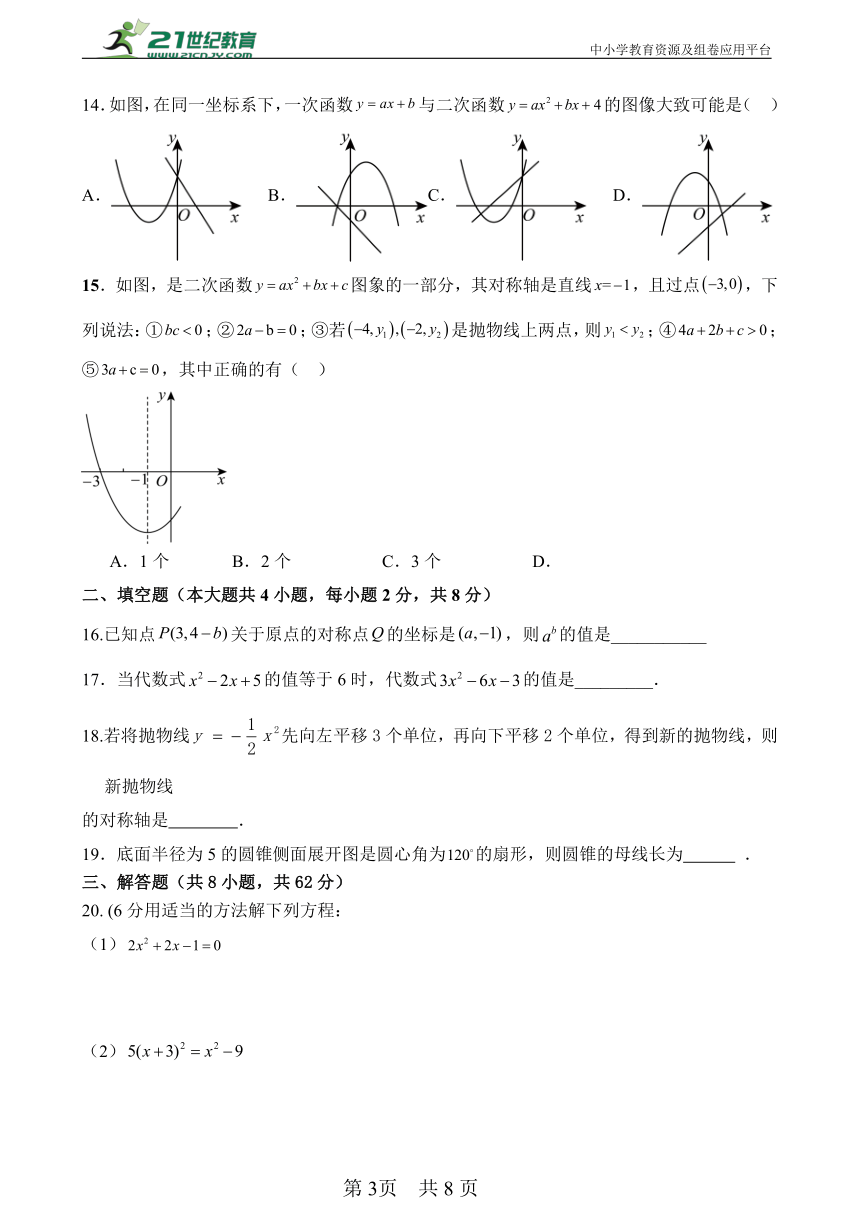
14.如图,在同一坐标系下,一次函数与二次函数的图像大致可能是( )
A. B.C. D.
15.如图,是二次函数图象的一部分,其对称轴是直线,且过点,下列说法:①;②;③若是抛物线上两点,则;④;⑤,其中正确的有( )
A.1个 B.2个 C.3个 D.
二、填空题(本大题共4小题,每小题2分,共8分)
16.已知点关于原点的对称点的坐标是,则的值是___________
17.当代数式的值等于6时,代数式的值是_________.
18.若将抛物线先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线
的对称轴是 .
19.底面半径为5的圆锥侧面展开图是圆心角为的扇形,则圆锥的母线长为 .
三、解答题(共8小题,共62分)
20. (6分用适当的方法解下列方程:
(1)
(2)
22.(7分)现有一个六面分别标有数字1,2,3,4,5,6且质地均匀的正方形骰子,另有三张正面分别标有数字1,2,3的卡片(卡片除数字外,其他都相同),先由小明投骰子一次,记下骰子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字.
(1)请用列表或画树形图(树状图)的方法,求出骰子向上一面出现的数字与卡片上的数字之积为6的概率;
(2)小明和小王做游戏,约定游戏规则如下:若骰子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若骰子向上一面出现的数字与卡片上的数字之积小于7,则小王赢,问小明和小王谁赢的可能性更大?请说明理由.
23.(7分)如图,某小区规划在长32米,宽20米的矩形场地ABCD上修建三条同样宽的3条小路,使其中两条与AB平行,一条与AD平行,其余部分种植草坪,若使草坪的面积为570米,问小路宽为多少米?
24.(7分)方程是关于的一元二次方程.
(1)若这个方程有两个不相等的实数根,求的取值范围;
(2)若等腰三角形的三边分别用表示,其中一边长为4,另外两边长恰好是这方程的两个根,求的周长.
25.(8分)某商店购进一批成本为每件30元的商品,经调查发现,当售价为每件60元时,每天销售量是40件,而销售单价每下降2元,每天的销售量就增加4件,且规定商品售价不低于成本价.设每件商品的售价为x元时,每天的销售量为y件.
(1)请求出y与x之间的函数关系式;
(2)当售价定为多少元时,能使销售该商品每天获得的利润(元)最大?最大利润是多少元?
26.(9分)如图,是的直径,为上一点,点在的延长线上,.
(1)求证:是的切线;
(2)若,的半径为,求圆中阴影部分的面积.
27.(12分)已知二次函数的图象与x轴分别交于A,B两点(点A位于点B的左侧),与y轴交于点C,连接.
(1)求A、B两点的坐标;
(2)点D是y轴上任意一点,连接,使得,在抛物线的对称轴上是否存在一点E,使得最小,若存在,请求出点E的坐标;若不存在,请说明理由;
(3)已知和是抛物线上任意两点,当时,求代数式的值.
答案与解析
一、单选题
1. B
2. A
3. D.
4. D.
5. B.
6. B
7. D.
8. B.
9. B.
10. B.
11. A.
12. C.
13. B.
14. C.
15. D
二、填空题
16. .
17. (a+2b)(a-2b) .
18. 15
19.2.
三、解答题
20.解方程.
(1)解:,
,
,
∴,
解得,
(2)解:
这里,,,
∴,
∴ ,
解得,
21.
22.
解:(1)如图所示:
共18种情况,数字之积为6的情况数有3种,P(数字之积为6)==.
(2)由上表可知,该游戏所有可能的结果共18种,其中骰子向上一面出现的数字与卡片上的数字之积大于7的有7种,骰子向上一面出现的数字与卡片上的数字之积小于7的有11种,所以小明赢的概率=,小王赢的概率=,故小王赢的可能性更大.
23.
解:设小路宽为x米,则种植草坪的六块区域可合成长为米、宽为米的矩形,
根据题意得:,
整理得:,
解得:,不符合题意,舍去.
答:小路宽为1米.
24.
(1)解:方程有两个不相等的实数根,
,解得:.
(2)解:①当时,则,解得,
把代入原方程得:
方程可化为解方程得,所以,
的周长;
②当或时,
把代入方程,可解得
当时,方程化为,解得.
即为或,不符合题意,舍去.
所以综合①②,的周长为10.
25.
(1)解:由题意得,,
∴与x之间的函数关系式为;
(2)解:由题意得,
∵,
∴当时,W的值最大,最大值为1250元.
答:当售价定为55元时,销售该商品每天获得的利润最大,最大利润是1250元.
26.
解:(1)证明:连接,
∵是的直径,
∴,
∵,
∴,
∵,
∴,
∴,即,
∴是的切线;
(2)解:过点C作于点E,
∵,,
∴,
∴,,
∵的半径为,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
27.
(1)解:存在,理由如下:
∵二次函数的图象与x轴分别交于A,B两点(点A位于点B的左侧),与y轴交于点C,
∴令,则,
解得
令,则,
即:,,,
对称轴为直线,
在y轴上找到一点D,连接,如图,
,
在中,,
,
即
点A关于对称轴的对称点为点B,连接交对称轴于点E,
则线段的长为的最小值.
设直线:,代入和,
得:
解得
直线:,
令,则,
故;
(2)解:,
和关于对称轴直线对称,
则,
,
答案与解析
一、单选题
1. B
2. A
3. D.
4. D.
5. B.
6. B
7. D.
8. B.
9. B.
10. B.
11. A.
12. C.
13. B.
14. C.
15. D
二、填空题
16. .
17. (a+2b)(a-2b) .
18. 15
19.2.
三、解答题
20.解方程.
(1)解:,
,
,
∴,
解得,
(2)解:
这里,,,
∴,
∴ ,
解得,
21.
22.
解:(1)如图所示:
共18种情况,数字之积为6的情况数有3种,P(数字之积为6)==.
(2)由上表可知,该游戏所有可能的结果共18种,其中骰子向上一面出现的数字与卡片上的数字之积大于7的有7种,骰子向上一面出现的数字与卡片上的数字之积小于7的有11种,所以小明赢的概率=,小王赢的概率=,故小王赢的可能性更大.
23.
解:设小路宽为x米,则种植草坪的六块区域可合成长为米、宽为米的矩形,
根据题意得:,
整理得:,
解得:,不符合题意,舍去.
答:小路宽为1米.
24.
(1)解:方程有两个不相等的实数根,
,解得:.
(2)解:①当时,则,解得,
把代入原方程得:
方程可化为解方程得,所以,
的周长;
②当或时,
把代入方程,可解得
当时,方程化为,解得.
即为或,不符合题意,舍去.
所以综合①②,的周长为10.
25.
(1)解:由题意得,,
∴与x之间的函数关系式为;
(2)解:由题意得,
∵,
∴当时,W的值最大,最大值为1250元.
答:当售价定为55元时,销售该商品每天获得的利润最大,最大利润是1250元.
26.
解:(1)证明:连接,
∵是的直径,
∴,
∵,
∴,
∵,
∴,
∴,即,
∴是的切线;
(2)解:过点C作于点E,
∵,,
∴,
∴,,
∵的半径为,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
27.
(1)解:存在,理由如下:
∵二次函数的图象与x轴分别交于A,B两点(点A位于点B的左侧),与y轴交于点C,
∴令,则,
解得
令,则,
即:,,,
对称轴为直线,
在y轴上找到一点D,连接,如图,
,
在中,,
,
即
点A关于对称轴的对称点为点B,连接交对称轴于点E,
则线段的长为的最小值.
设直线:,代入和,
得:
解得
直线:,
令,则,
故;
(2)解:,
和关于对称轴直线对称,
则,
,
PAGE
第6页 共8页
云南省2024—2025学年秋季学期九年级数学期末猜题卷
(全卷三个大题,共24个小题,共6页;满分100分;考试用时120分钟)
一、选择题(本大题共15小题,每小题只有一个正确选项,每小题2分,共30分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2. 下列说法错误是( )
A. 必然事件的概率为1 B. 心想事成是不可能事件
C. 平分弦(非直径)的直径垂直于弦 D. 三角形的内心到三边的距离相等
3.方程的根是( )
A. B. C. D.无实数根
4.若⊙O的半径为4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
5.某地2018年为做好“精准扶贫”,投入资金1480万元用于异地安置,并规划投入资金逐年增加,2020年在2018年的基础上增加投入资金2000万元.若设从2018年到2020年该地投入异地安置资金的年平均增长率为,则下列方程正确的是( )
A. B.
C. D.
6.关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )
A.k≤﹣ B.k≤﹣且k≠0 C.k≥﹣ D.k≥﹣且k≠0
7.如图,四边形是的内接四边形,若,则的度数为( )
A. B. C. D.
8.如图,平面直角坐标系中,点在第一象限,点在轴的正半轴上,,,将绕点逆时针旋转,点的对应点的坐标是( )
A.
B.
C.
D.
9.如图,在中,分别以,为圆心,大于的长为半径画弧,两弧交于点,,作直线,分别交,于点,,连接.若,则的度数为( )
A. B. C. D.
10.如图是半径为4的的内接正六边形,则圆心O到边的距离是( )
A.4 B. C.2 D.
11.关于二次函数,下列说法正确的是( )
A.顶点坐标为 B.其图象的对称轴为直线
C.最小值为2 D.当时,y随x的增大而增小
12.一列单项式按以下规律排列:x,,,,,,,…,则第2024个单项式是( )
A. B. C. D.
13.要在一个三角形铁皮上截下一个面积最大的圆,此圆圆心应在三角形( )
A.三边高线的交点 B.三个角的平分线的交点
C.三边垂直平分线的交点 D.三边中线的交点
14.如图,在同一坐标系下,一次函数与二次函数的图像大致可能是( )
A. B.C. D.
15.如图,是二次函数图象的一部分,其对称轴是直线,且过点,下列说法:①;②;③若是抛物线上两点,则;④;⑤,其中正确的有( )
A.1个 B.2个 C.3个 D.
二、填空题(本大题共4小题,每小题2分,共8分)
16.已知点关于原点的对称点的坐标是,则的值是___________
17.当代数式的值等于6时,代数式的值是_________.
18.若将抛物线先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线
的对称轴是 .
19.底面半径为5的圆锥侧面展开图是圆心角为的扇形,则圆锥的母线长为 .
三、解答题(共8小题,共62分)
20. (6分用适当的方法解下列方程:
(1)
(2)
22.(7分)现有一个六面分别标有数字1,2,3,4,5,6且质地均匀的正方形骰子,另有三张正面分别标有数字1,2,3的卡片(卡片除数字外,其他都相同),先由小明投骰子一次,记下骰子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字.
(1)请用列表或画树形图(树状图)的方法,求出骰子向上一面出现的数字与卡片上的数字之积为6的概率;
(2)小明和小王做游戏,约定游戏规则如下:若骰子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若骰子向上一面出现的数字与卡片上的数字之积小于7,则小王赢,问小明和小王谁赢的可能性更大?请说明理由.
23.(7分)如图,某小区规划在长32米,宽20米的矩形场地ABCD上修建三条同样宽的3条小路,使其中两条与AB平行,一条与AD平行,其余部分种植草坪,若使草坪的面积为570米,问小路宽为多少米?
24.(7分)方程是关于的一元二次方程.
(1)若这个方程有两个不相等的实数根,求的取值范围;
(2)若等腰三角形的三边分别用表示,其中一边长为4,另外两边长恰好是这方程的两个根,求的周长.
25.(8分)某商店购进一批成本为每件30元的商品,经调查发现,当售价为每件60元时,每天销售量是40件,而销售单价每下降2元,每天的销售量就增加4件,且规定商品售价不低于成本价.设每件商品的售价为x元时,每天的销售量为y件.
(1)请求出y与x之间的函数关系式;
(2)当售价定为多少元时,能使销售该商品每天获得的利润(元)最大?最大利润是多少元?
26.(9分)如图,是的直径,为上一点,点在的延长线上,.
(1)求证:是的切线;
(2)若,的半径为,求圆中阴影部分的面积.
27.(12分)已知二次函数的图象与x轴分别交于A,B两点(点A位于点B的左侧),与y轴交于点C,连接.
(1)求A、B两点的坐标;
(2)点D是y轴上任意一点,连接,使得,在抛物线的对称轴上是否存在一点E,使得最小,若存在,请求出点E的坐标;若不存在,请说明理由;
(3)已知和是抛物线上任意两点,当时,求代数式的值.
答案与解析
一、单选题
1. B
2. A
3. D.
4. D.
5. B.
6. B
7. D.
8. B.
9. B.
10. B.
11. A.
12. C.
13. B.
14. C.
15. D
二、填空题
16. .
17. (a+2b)(a-2b) .
18. 15
19.2.
三、解答题
20.解方程.
(1)解:,
,
,
∴,
解得,
(2)解:
这里,,,
∴,
∴ ,
解得,
21.
22.
解:(1)如图所示:
共18种情况,数字之积为6的情况数有3种,P(数字之积为6)==.
(2)由上表可知,该游戏所有可能的结果共18种,其中骰子向上一面出现的数字与卡片上的数字之积大于7的有7种,骰子向上一面出现的数字与卡片上的数字之积小于7的有11种,所以小明赢的概率=,小王赢的概率=,故小王赢的可能性更大.
23.
解:设小路宽为x米,则种植草坪的六块区域可合成长为米、宽为米的矩形,
根据题意得:,
整理得:,
解得:,不符合题意,舍去.
答:小路宽为1米.
24.
(1)解:方程有两个不相等的实数根,
,解得:.
(2)解:①当时,则,解得,
把代入原方程得:
方程可化为解方程得,所以,
的周长;
②当或时,
把代入方程,可解得
当时,方程化为,解得.
即为或,不符合题意,舍去.
所以综合①②,的周长为10.
25.
(1)解:由题意得,,
∴与x之间的函数关系式为;
(2)解:由题意得,
∵,
∴当时,W的值最大,最大值为1250元.
答:当售价定为55元时,销售该商品每天获得的利润最大,最大利润是1250元.
26.
解:(1)证明:连接,
∵是的直径,
∴,
∵,
∴,
∵,
∴,
∴,即,
∴是的切线;
(2)解:过点C作于点E,
∵,,
∴,
∴,,
∵的半径为,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
27.
(1)解:存在,理由如下:
∵二次函数的图象与x轴分别交于A,B两点(点A位于点B的左侧),与y轴交于点C,
∴令,则,
解得
令,则,
即:,,,
对称轴为直线,
在y轴上找到一点D,连接,如图,
,
在中,,
,
即
点A关于对称轴的对称点为点B,连接交对称轴于点E,
则线段的长为的最小值.
设直线:,代入和,
得:
解得
直线:,
令,则,
故;
(2)解:,
和关于对称轴直线对称,
则,
,
答案与解析
一、单选题
1. B
2. A
3. D.
4. D.
5. B.
6. B
7. D.
8. B.
9. B.
10. B.
11. A.
12. C.
13. B.
14. C.
15. D
二、填空题
16. .
17. (a+2b)(a-2b) .
18. 15
19.2.
三、解答题
20.解方程.
(1)解:,
,
,
∴,
解得,
(2)解:
这里,,,
∴,
∴ ,
解得,
21.
22.
解:(1)如图所示:
共18种情况,数字之积为6的情况数有3种,P(数字之积为6)==.
(2)由上表可知,该游戏所有可能的结果共18种,其中骰子向上一面出现的数字与卡片上的数字之积大于7的有7种,骰子向上一面出现的数字与卡片上的数字之积小于7的有11种,所以小明赢的概率=,小王赢的概率=,故小王赢的可能性更大.
23.
解:设小路宽为x米,则种植草坪的六块区域可合成长为米、宽为米的矩形,
根据题意得:,
整理得:,
解得:,不符合题意,舍去.
答:小路宽为1米.
24.
(1)解:方程有两个不相等的实数根,
,解得:.
(2)解:①当时,则,解得,
把代入原方程得:
方程可化为解方程得,所以,
的周长;
②当或时,
把代入方程,可解得
当时,方程化为,解得.
即为或,不符合题意,舍去.
所以综合①②,的周长为10.
25.
(1)解:由题意得,,
∴与x之间的函数关系式为;
(2)解:由题意得,
∵,
∴当时,W的值最大,最大值为1250元.
答:当售价定为55元时,销售该商品每天获得的利润最大,最大利润是1250元.
26.
解:(1)证明:连接,
∵是的直径,
∴,
∵,
∴,
∵,
∴,
∴,即,
∴是的切线;
(2)解:过点C作于点E,
∵,,
∴,
∴,,
∵的半径为,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
27.
(1)解:存在,理由如下:
∵二次函数的图象与x轴分别交于A,B两点(点A位于点B的左侧),与y轴交于点C,
∴令,则,
解得
令,则,
即:,,,
对称轴为直线,
在y轴上找到一点D,连接,如图,
,
在中,,
,
即
点A关于对称轴的对称点为点B,连接交对称轴于点E,
则线段的长为的最小值.
设直线:,代入和,
得:
解得
直线:,
令,则,
故;
(2)解:,
和关于对称轴直线对称,
则,
,
PAGE
第6页 共8页
同课章节目录
