第6章 一次方程组 学情评估卷(含答案)华师版数学七年级下册(2024)
文档属性
| 名称 | 第6章 一次方程组 学情评估卷(含答案)华师版数学七年级下册(2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 90.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 11:15:40 | ||
图片预览




文档简介
第6章学情评估卷
一、选择题(每小题3分,共30分,下列各小题均有四个选项,其中只有一个是正确的)
1.下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
2.已知二元一次方程,用的代数式表示,正确的是( )
A. B. C. D.
3.下列方程组:其中用加减消元法解较为简便的是( )
A.①② B.①③ C.②③ D.①②③
4.已知与都是方程的解,则与的值分别为( )
A., B.,4 C.,4 D.,
5.已知,当取一个确定的值时,就会得到一个关于,的二元一次方程,所有这些方程有一个公共解,则这个公共解是( )
A. B. C. D.
6.如图①是一个长为,宽为的长方形,将这样四个完全相同的长方形摆放在一个长为5,宽为4的大长方形中,如图②所示,则图②中阴影部分的面积是( )
A.8 B.12 C.15 D.16
7.若方程组的解为则被“”和“”遮挡的两个数分别是( )
A.7,9 B.9,7 C.1, D.,1
8.学校组织劳技社会实践活动,甲、乙两班同时参加了陶艺品制作项目.活动结束后,两个班统计了制作陶艺品的总数,结果发现甲、乙两班制作的陶艺品的总数比为,甲班制作的陶艺品总数的2倍比乙班制作的陶艺品总数的3倍少30个.设甲、乙两班制作的陶艺品的总数分别为个和个,根据题意,可列方程组为( )
A. B.
C. D.
9.已知方程组的解是则方程组的解是( )
A. B. C. D.
10.小月去买文具,打算买5支单价相同的签字笔和3本单价相同的笔记本,她与售货员的对话如下,那么购买一支签字笔和一本笔记本应付( )
小月:“您好,我要买5支单价相同的签字笔和3本单价相同的笔记本.” 售货员:“好的,那你应付款52元.” 小月:“刚才我把两种文具的单价弄反了,以为要付44元.”
A.11元 B.12元 C.13元 D.14元
二、填空题(每小题3分,共15分)
11.请写出一个二元一次方程:____________________________,使该方程的解为
12.若方程,与有公共解,则______.
13.已知则______.
14.《九章算术》中有这样一个问题:若2人坐一辆车,则9人需要步行,若…….问:人与车各多少?小明同学设有辆车,人数为,根据题意,可列方程组为根据已有信息,题中用“……”表示的缺失条件应补为________________________________,__.
15.在某市举行的中学生运动会初中组足球项目比赛中,某足球队共进行了8场比赛,得了12分,根据比赛规定:胜一场得3分,平一场得1分,负一场得0分,则该队获胜的场数有______种可能.
三、解答题(本大题共8个小题,共75分)
16.(10分)解二元一次方程组:
(1)
(2)
17.(8分)已知关于,的二元一次方程组甲同学正确解得而乙同学粗心,把看错了,解得求的值.
18.(9分)已知关于,的方程组其中常数.
(1) 直接写出的值(结果用含 的代数式表示);
(2) 无论取何值,试说明的值总是不变的.
19.(8分)学校和博物馆相距20千米,小明与小强分别从学校和博物馆出发,相向而行.如果小明比小强早出发30分钟,那么在小强出发2小时后,他们相遇;如果他们同时出发,那么1小时后两人还相距11千米.求小明、小强每小时各走多少千米.
20.(9分)定义:数对经过一种运算可以得到数对,将该运算记作:,其中(,为常数).
例如:当,时,.
(1) 当,时,求数对经过运算得到的数对;
(2) 若,求和的值.
21.(9分)阅读材料:善于思考的小明在解方程组时,采用了一种“整体代换”的解法,解法如下:
解:将方程②变形为,③
把方程①代入③,得,解得,把代入①,得, 方程组的解为
请你解决以下问题:
(1) 试用小明的“整体代换”的方法解方程组
(2) 已知,,满足 试求的值.
22.(10分)放学后,小贤和小艺来到学校附近的超市里购买一种特殊型号的笔芯和卡通笔记本,这种笔芯每盒10支,如果整盒买比单支买每支可优惠0.5元,小贤买3支笔芯,2本笔记本需花费19元,小艺买7支笔芯,1本笔记本需花费26元.
(1) 求笔记本的单价和单独购买一支笔芯的价格;
(2) 小贤和小艺都还想再买一件单价为3元的小工艺品,但他们各自为要买的文具付款后,只有小贤还剩2元钱,他们要怎样做才能既买到各自的文具,又都买到小工艺品,请通过运算说明.
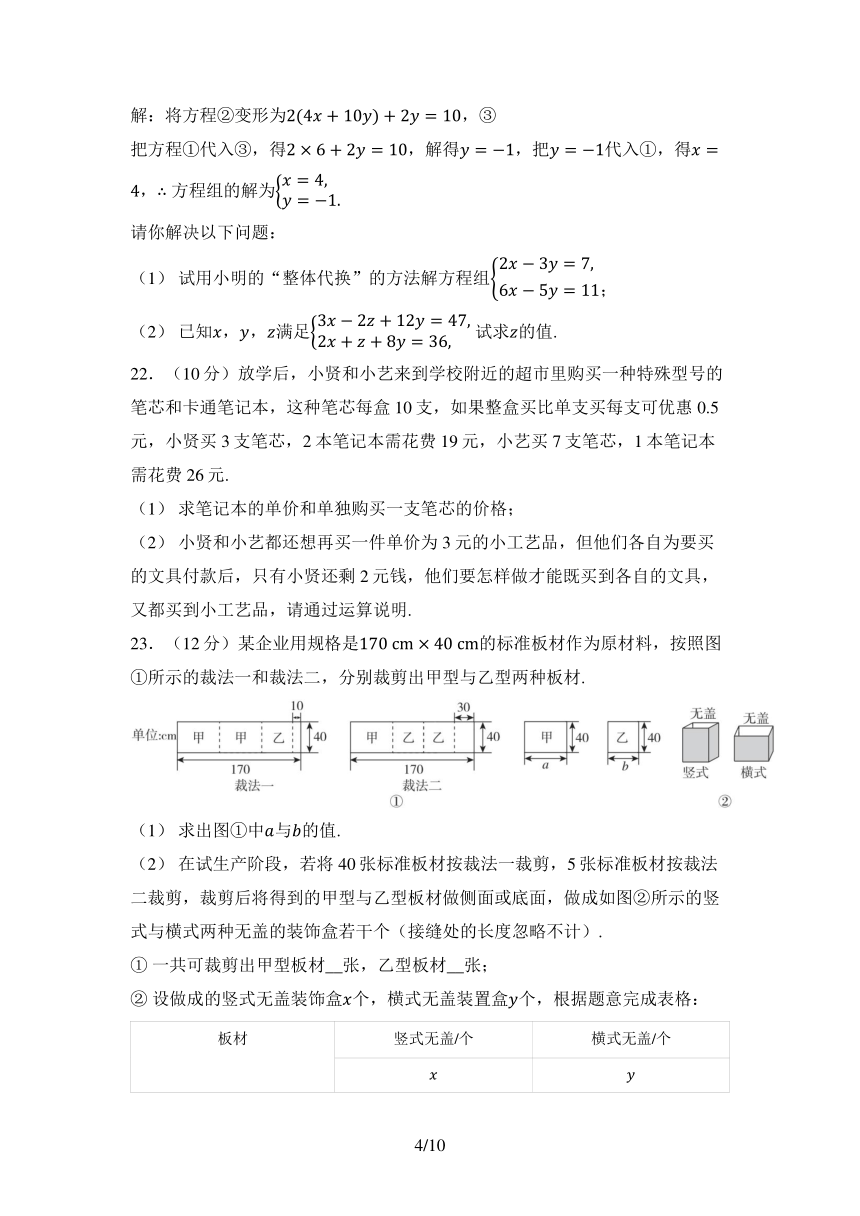
23.(12分)某企业用规格是的标准板材作为原材料,按照图①所示的裁法一和裁法二,分别裁剪出甲型与乙型两种板材.
(1) 求出图①中与的值.
(2) 在试生产阶段,若将40张标准板材按裁法一裁剪,5张标准板材按裁法二裁剪,裁剪后将得到的甲型与乙型板材做侧面或底面,做成如图②所示的竖式与横式两种无盖的装饰盒若干个(接缝处的长度忽略不计).
① 一共可裁剪出甲型板材__张,乙型板材__张;
② 设做成的竖式无盖装饰盒个,横式无盖装置盒个,根据题意完成表格:
板材 竖式无盖/个 横式无盖/个
甲型/张
乙型/张
③ 恰好一共可以做出竖式和横式两种无盖装饰盒多少个?
【参考答案】
第6章学情评估卷
一、选择题(每小题3分,共30分,下列各小题均有四个选项,其中只有一个是正确的)
1.C
2.C
3.C
4.A
5.A
6.B
7.A
8.C
9.B
[解析]点拨:由方程组
得
方程组的解是
方程组的解为
10.B
[解析]点拨:设签字笔的单价为元,笔记本的单价为元,
则
,得,
.
购买一支签字笔和一本笔记本应付12元.
二、填空题(每小题3分,共15分)
11.(答案不唯一)
12.4
13.1
[解析]点拨:
,得,
,,得,
,
.
14.3人坐一辆车,则有两辆空车; 39
15.3
[解析]点拨:设该队胜场,平场,则负场,依题意,得,
,
又,
该队可能获胜2场、3场或4场.
故该队获胜的场数有3种可能.
三、解答题(本大题共8个小题,共75分)
16.(1) 解:,得,
解得.
把代入①,得,
原方程组的解为
(2) 原方程组整理,得
,得,
解得.
把代入③,得,
原方程组的解为
17.解:
将代入方程②,得,解得.
将代入方程①,得,③
将代入方程①,得,④
联立③④,得
解得
所以.
18.(1) 解:.
(2) 由(1)知,③
,得,
.
把代入③,得,
,
无论取何值,的值总是不变的.
19.解:设小明每小时走千米,小强每小时走千米,
根据题意,得
解得
答:小明每小时走4千米,小强每小时走5千米.
20.(1) 解:当,时,
,,
,,
.
(2) ,
解得
和的值分别为,.
21.(1) 解:
将②变形,得,③
将①代入③,得,
解得,
把代入①,得,
方程组的解为
(2)
由①,得,③
由②,得,④
,得,
解得.
22.(1) 解:设单独购买一支笔芯的价格为元,一本笔记本的价格为元,
根据题意,得
解得
笔记本的单价为5元,单独购买一支笔芯的价格为3元.
(2) 由题意得要买到小工艺品可以两人一起合买笔芯.
一起买笔芯后,小贤剩余的钱为(元),
小艺剩余的钱为(元).
因为,所以两人一起合买笔芯能既买到各自的文具,又都买到小工艺品.
23.(1) 解:根据题意,得
解得
(2) ① 85; 50
② ;;;
③ 根据题意,得
解得
.
故恰好一共可以做出竖式和横式两种无盖装饰盒27个.
/
一、选择题(每小题3分,共30分,下列各小题均有四个选项,其中只有一个是正确的)
1.下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
2.已知二元一次方程,用的代数式表示,正确的是( )
A. B. C. D.
3.下列方程组:其中用加减消元法解较为简便的是( )
A.①② B.①③ C.②③ D.①②③
4.已知与都是方程的解,则与的值分别为( )
A., B.,4 C.,4 D.,
5.已知,当取一个确定的值时,就会得到一个关于,的二元一次方程,所有这些方程有一个公共解,则这个公共解是( )
A. B. C. D.
6.如图①是一个长为,宽为的长方形,将这样四个完全相同的长方形摆放在一个长为5,宽为4的大长方形中,如图②所示,则图②中阴影部分的面积是( )
A.8 B.12 C.15 D.16
7.若方程组的解为则被“”和“”遮挡的两个数分别是( )
A.7,9 B.9,7 C.1, D.,1
8.学校组织劳技社会实践活动,甲、乙两班同时参加了陶艺品制作项目.活动结束后,两个班统计了制作陶艺品的总数,结果发现甲、乙两班制作的陶艺品的总数比为,甲班制作的陶艺品总数的2倍比乙班制作的陶艺品总数的3倍少30个.设甲、乙两班制作的陶艺品的总数分别为个和个,根据题意,可列方程组为( )
A. B.
C. D.
9.已知方程组的解是则方程组的解是( )
A. B. C. D.
10.小月去买文具,打算买5支单价相同的签字笔和3本单价相同的笔记本,她与售货员的对话如下,那么购买一支签字笔和一本笔记本应付( )
小月:“您好,我要买5支单价相同的签字笔和3本单价相同的笔记本.” 售货员:“好的,那你应付款52元.” 小月:“刚才我把两种文具的单价弄反了,以为要付44元.”
A.11元 B.12元 C.13元 D.14元
二、填空题(每小题3分,共15分)
11.请写出一个二元一次方程:____________________________,使该方程的解为
12.若方程,与有公共解,则______.
13.已知则______.
14.《九章算术》中有这样一个问题:若2人坐一辆车,则9人需要步行,若…….问:人与车各多少?小明同学设有辆车,人数为,根据题意,可列方程组为根据已有信息,题中用“……”表示的缺失条件应补为________________________________,__.
15.在某市举行的中学生运动会初中组足球项目比赛中,某足球队共进行了8场比赛,得了12分,根据比赛规定:胜一场得3分,平一场得1分,负一场得0分,则该队获胜的场数有______种可能.
三、解答题(本大题共8个小题,共75分)
16.(10分)解二元一次方程组:
(1)
(2)
17.(8分)已知关于,的二元一次方程组甲同学正确解得而乙同学粗心,把看错了,解得求的值.
18.(9分)已知关于,的方程组其中常数.
(1) 直接写出的值(结果用含 的代数式表示);
(2) 无论取何值,试说明的值总是不变的.
19.(8分)学校和博物馆相距20千米,小明与小强分别从学校和博物馆出发,相向而行.如果小明比小强早出发30分钟,那么在小强出发2小时后,他们相遇;如果他们同时出发,那么1小时后两人还相距11千米.求小明、小强每小时各走多少千米.
20.(9分)定义:数对经过一种运算可以得到数对,将该运算记作:,其中(,为常数).
例如:当,时,.
(1) 当,时,求数对经过运算得到的数对;
(2) 若,求和的值.
21.(9分)阅读材料:善于思考的小明在解方程组时,采用了一种“整体代换”的解法,解法如下:
解:将方程②变形为,③
把方程①代入③,得,解得,把代入①,得, 方程组的解为
请你解决以下问题:
(1) 试用小明的“整体代换”的方法解方程组
(2) 已知,,满足 试求的值.
22.(10分)放学后,小贤和小艺来到学校附近的超市里购买一种特殊型号的笔芯和卡通笔记本,这种笔芯每盒10支,如果整盒买比单支买每支可优惠0.5元,小贤买3支笔芯,2本笔记本需花费19元,小艺买7支笔芯,1本笔记本需花费26元.
(1) 求笔记本的单价和单独购买一支笔芯的价格;
(2) 小贤和小艺都还想再买一件单价为3元的小工艺品,但他们各自为要买的文具付款后,只有小贤还剩2元钱,他们要怎样做才能既买到各自的文具,又都买到小工艺品,请通过运算说明.
23.(12分)某企业用规格是的标准板材作为原材料,按照图①所示的裁法一和裁法二,分别裁剪出甲型与乙型两种板材.
(1) 求出图①中与的值.
(2) 在试生产阶段,若将40张标准板材按裁法一裁剪,5张标准板材按裁法二裁剪,裁剪后将得到的甲型与乙型板材做侧面或底面,做成如图②所示的竖式与横式两种无盖的装饰盒若干个(接缝处的长度忽略不计).
① 一共可裁剪出甲型板材__张,乙型板材__张;
② 设做成的竖式无盖装饰盒个,横式无盖装置盒个,根据题意完成表格:
板材 竖式无盖/个 横式无盖/个
甲型/张
乙型/张
③ 恰好一共可以做出竖式和横式两种无盖装饰盒多少个?
【参考答案】
第6章学情评估卷
一、选择题(每小题3分,共30分,下列各小题均有四个选项,其中只有一个是正确的)
1.C
2.C
3.C
4.A
5.A
6.B
7.A
8.C
9.B
[解析]点拨:由方程组
得
方程组的解是
方程组的解为
10.B
[解析]点拨:设签字笔的单价为元,笔记本的单价为元,
则
,得,
.
购买一支签字笔和一本笔记本应付12元.
二、填空题(每小题3分,共15分)
11.(答案不唯一)
12.4
13.1
[解析]点拨:
,得,
,,得,
,
.
14.3人坐一辆车,则有两辆空车; 39
15.3
[解析]点拨:设该队胜场,平场,则负场,依题意,得,
,
又,
该队可能获胜2场、3场或4场.
故该队获胜的场数有3种可能.
三、解答题(本大题共8个小题,共75分)
16.(1) 解:,得,
解得.
把代入①,得,
原方程组的解为
(2) 原方程组整理,得
,得,
解得.
把代入③,得,
原方程组的解为
17.解:
将代入方程②,得,解得.
将代入方程①,得,③
将代入方程①,得,④
联立③④,得
解得
所以.
18.(1) 解:.
(2) 由(1)知,③
,得,
.
把代入③,得,
,
无论取何值,的值总是不变的.
19.解:设小明每小时走千米,小强每小时走千米,
根据题意,得
解得
答:小明每小时走4千米,小强每小时走5千米.
20.(1) 解:当,时,
,,
,,
.
(2) ,
解得
和的值分别为,.
21.(1) 解:
将②变形,得,③
将①代入③,得,
解得,
把代入①,得,
方程组的解为
(2)
由①,得,③
由②,得,④
,得,
解得.
22.(1) 解:设单独购买一支笔芯的价格为元,一本笔记本的价格为元,
根据题意,得
解得
笔记本的单价为5元,单独购买一支笔芯的价格为3元.
(2) 由题意得要买到小工艺品可以两人一起合买笔芯.
一起买笔芯后,小贤剩余的钱为(元),
小艺剩余的钱为(元).
因为,所以两人一起合买笔芯能既买到各自的文具,又都买到小工艺品.
23.(1) 解:根据题意,得
解得
(2) ① 85; 50
② ;;;
③ 根据题意,得
解得
.
故恰好一共可以做出竖式和横式两种无盖装饰盒27个.
/
