期末测试卷(含答案)华师版数学七年级下册(2024)
文档属性
| 名称 | 期末测试卷(含答案)华师版数学七年级下册(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 186.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 11:19:27 | ||
图片预览




文档简介
期末综合测试卷
一、选择题(本大题共8小题,每小题3分,共24分)
1.[2024·长春期末]如图有关环保的四个图形中,是中心对称图形的是( )
A. B.
C. D.
2.已知是关于的方程的解,则的值是( )
A. B. C. D.8
3.已知一个三角形的两边长分别为和,则该三角形第三边的长不可能是( )
A. B. C. D.
4.把方程改写成“用含的式子表示”的形式,正确的是( )
A. B. C. D.
5.下面解方程的过程,你认为正确的是( )
A.方程,合并同类项,得
B.方程,去括号,得
C.方程,去分母,得
D.方程,系数化为1,得
6.二十边形的内角和是( )
A. B. C. D.
7.若关于的不等式组仅有3个整数解,则的取值范围是( )
A. B.
C. D.
8.如图,在两个长、宽都分别为、的大长方形中,有若干个形状、大小完全相同的小长方形,拼成了“南开”两字,则每个小长方形的面积为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
9.若,则______.(填“ ”“”或“ ”)
10.[2024·长春期末]不等式的非负整数解为______.
11.关于,的二元一次方程组的解满足,则的值是__________.
12.如图,将沿着射线的方向平移到的位置,若点是的中点,,则平移的距离为______.
(第12题)
13.《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:买鸡的人数和鸡的价格各是多少?”设有个人共同出钱买鸡,根据题意,可列一元一次方程为____________________.
14.如图,是的角平分线,是的高, , ,点为边上一点,当为直角三角形时,的度数为______________________.
(第14题)
三、解答题(本大题共10小题,共78分)
15.(6分)解不等式,并把解集在数轴上表示出来:.
16.(6分)解方程:.
17.(6分)解方程组:
18.(7分)下面是小明同学解不等式组的过程,请认真阅读,完成相应的任务.
解:由不等式①,得, 第一步
解得. 第二步
由不等式②,得, 第三步
移项,得, 第四步
合并同类项,得, 第五步
解得.第六步
所以,原不等式组的解集是.第七步
任务一:
(1) 小明的解答过程中,第三步的依据是__________________________;
(2) 第__步开始出现错误,错误的原因是______________________________________________________;
任务二:
(3) 求这个不等式组正确的解集.
19.(7分)先阅读材料,再解方程组.
解方程组 时,可由①得,③然后再将③代入②,得
,解得,从而进一步得 这种方法被称为“整体代入法”.
请用上述方法解方程组:
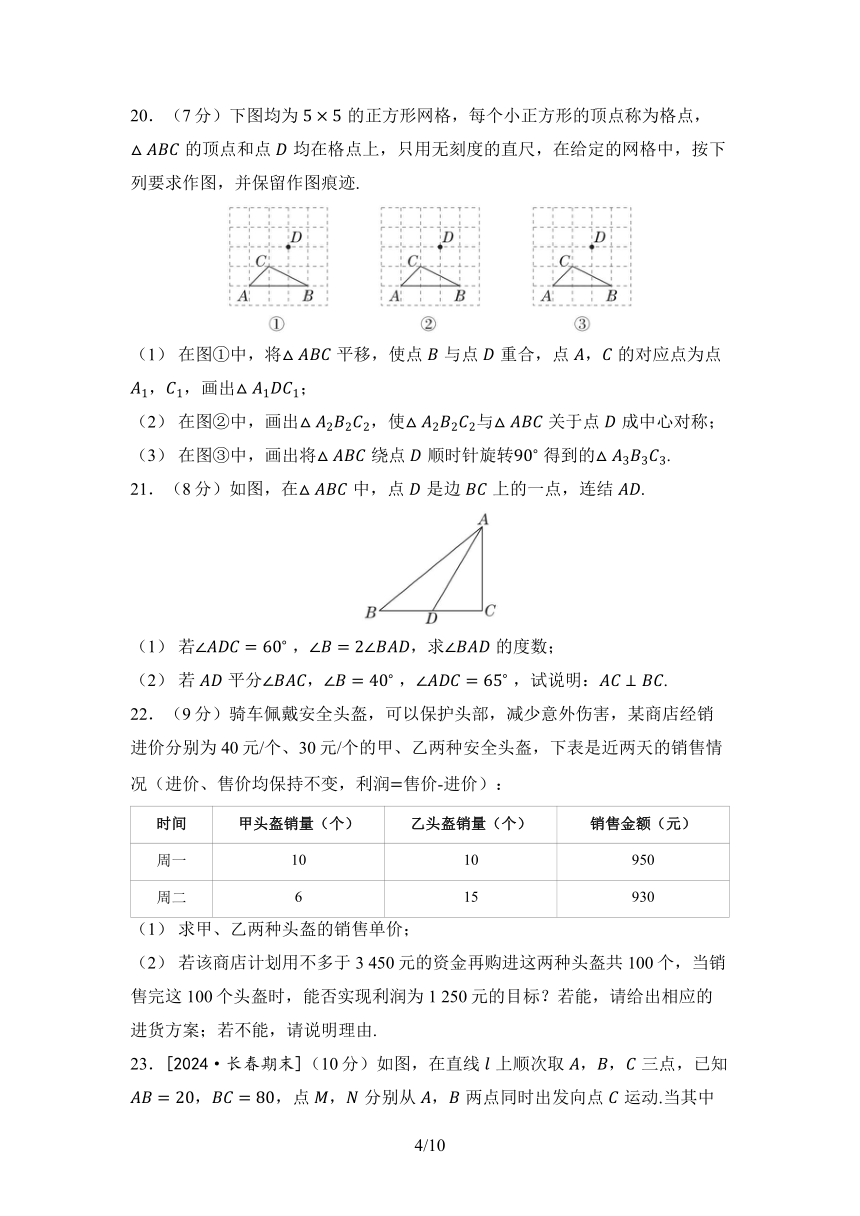
20.(7分)下图均为的正方形网格,每个小正方形的顶点称为格点,的顶点和点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图,并保留作图痕迹.
(1) 在图①中,将平移,使点与点重合,点,的对应点为点,,画出;
(2) 在图②中,画出,使与关于点成中心对称;
(3) 在图③中,画出将绕点顺时针旋转 得到的.
21.(8分)如图,在中,点是边上的一点,连结.
(1) 若 ,,求的度数;
(2) 若平分, , ,试说明:.
22.(9分)骑车佩戴安全头盔,可以保护头部,减少意外伤害,某商店经销进价分别为40元/个、30元/个的甲、乙两种安全头盔,下表是近两天的销售情况(进价、售价均保持不变,利润售价-进价)
时间 甲头盔销量(个) 乙头盔销量(个) 销售金额(元)
周一 10 10 950
周二 6 15 930
(1) 求甲、乙两种头盔的销售单价;
(2) 若该商店计划用不多于3 450元的资金再购进这两种头盔共100个,当销售完这100个头盔时,能否实现利润为1 250元的目标?若能,请给出相应的进货方案;若不能,请说明理由.
23.[2024·长春期末](10分)如图,在直线上顺次取,,三点,已知,,点,分别从,两点同时出发向点运动.当其中一动点到达点时,,同时停止运动.已知点的速度为每秒2个单位长度,点的速度为每秒1个单位长度,设运动时间为秒.
(1) 用含的式子表示线段的长度为________;
(2) 当为何值时,,两点重合?
(3) 若点为中点,点为中点.问:为何值时,的长度为5?
24.(12分)
(1) 【问题背景】小明在学习多边形时,把如图①所示的图形看成“8”字形,并得出如下结论:,请你说明理由.
(2) 【尝试应用】如图②,、分别平分、,若 , ,求的度数.
小明结合(1)中的结论并利用方程思想轻松解答如下:
解:由、分别平分、,可设,,
由(1)的结论,得
…
请你帮小明把求解过程补充完整.
(3) 【拓展延伸】如图③,已知 , ,,,请利用上述结论或方法直接写出的度数.(用含 , 的代数式表示)
【参考答案】
一、选择题(本大题共8小题,每小题3分,共24分)
1.B
2.C
3.A
4.B
5.D
6.B
7.D
8.C
[解析]点拨:设每个小长方形的长为,宽为,
由题意得
解得
则每个小长方形的面积为.
二、填空题(本大题共6小题,每小题3分,共18分)
9.
10.0,1,2
11.
12.4
[解析]思路点睛:根据平移的性质得到,然后根据线段中点的定义得到,即可计算得到答案.
13.
14. 或
[解析]点拨:如图①所示,当 时,
是的角平分线, ,
,
;
如图②,当 时,
同理可得 .
是的高, ,
易知 ,
.
综上所述,的度数为 或 .
三、解答题(本大题共10小题,共78分)
15.解:去括号,得,
移项,得,
合并同类项,得,
系数化为1,得.
解集在数轴上的表示如图.
16.解:去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得.
17.解:,得,
解得,
将代入①,得,
解得,
所以原方程组的解为
18.(1) 解:不等式的基本性质2
(2) 六; 系数化为1时两边同乘负数没有改变不等号方向
(3) 由不等式①,得.
解得.
由不等式②,得.
解得.
所以原不等式组正确的解集是.
19.解:
由①,得,③
将③代入②,得,
解得,
将代入③,得,
解得.
故原方程组的解为
20.(1) 解:如图①,即为所作.
(2) 如图②,即为所作.
(3) 如图③,即为所作.
21.(1) 解: ,,,
,
.
(2) , ,
.
平分,
,
,
即.
22.(1) 解:设甲种头盔的销售单价为元,乙种头盔的销售单价为元,
依题意得
解得
答:甲种头盔的销售单价为55元,乙种头盔的销售单价为40元.
(2) 不能.理由如下:设购进甲种头盔个,则购进乙种头盔个,依题意得
解不等式①,得,
解方程②,得,
不存在符合题意的的值,即当销售完这100个头盔时,不能实现利润为1 250元的目标.
23.(1)
(2) 解:由题意得,,,
当,两点重合时,,
,
解得,
当时,、两点重合.
(3) 由题意得,,,
点为中点,点为中点.
,,
.
当点在点的左边时,,
解得;
当点在点的右边时,,
解得,
当或50时,的长度为5.
24.(1) 解:在中, ,
在中, .
,
.
(2) ,得,
即,
.
(3) .
/
一、选择题(本大题共8小题,每小题3分,共24分)
1.[2024·长春期末]如图有关环保的四个图形中,是中心对称图形的是( )
A. B.
C. D.
2.已知是关于的方程的解,则的值是( )
A. B. C. D.8
3.已知一个三角形的两边长分别为和,则该三角形第三边的长不可能是( )
A. B. C. D.
4.把方程改写成“用含的式子表示”的形式,正确的是( )
A. B. C. D.
5.下面解方程的过程,你认为正确的是( )
A.方程,合并同类项,得
B.方程,去括号,得
C.方程,去分母,得
D.方程,系数化为1,得
6.二十边形的内角和是( )
A. B. C. D.
7.若关于的不等式组仅有3个整数解,则的取值范围是( )
A. B.
C. D.
8.如图,在两个长、宽都分别为、的大长方形中,有若干个形状、大小完全相同的小长方形,拼成了“南开”两字,则每个小长方形的面积为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
9.若,则______.(填“ ”“”或“ ”)
10.[2024·长春期末]不等式的非负整数解为______.
11.关于,的二元一次方程组的解满足,则的值是__________.
12.如图,将沿着射线的方向平移到的位置,若点是的中点,,则平移的距离为______.
(第12题)
13.《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:买鸡的人数和鸡的价格各是多少?”设有个人共同出钱买鸡,根据题意,可列一元一次方程为____________________.
14.如图,是的角平分线,是的高, , ,点为边上一点,当为直角三角形时,的度数为______________________.
(第14题)
三、解答题(本大题共10小题,共78分)
15.(6分)解不等式,并把解集在数轴上表示出来:.
16.(6分)解方程:.
17.(6分)解方程组:
18.(7分)下面是小明同学解不等式组的过程,请认真阅读,完成相应的任务.
解:由不等式①,得, 第一步
解得. 第二步
由不等式②,得, 第三步
移项,得, 第四步
合并同类项,得, 第五步
解得.第六步
所以,原不等式组的解集是.第七步
任务一:
(1) 小明的解答过程中,第三步的依据是__________________________;
(2) 第__步开始出现错误,错误的原因是______________________________________________________;
任务二:
(3) 求这个不等式组正确的解集.
19.(7分)先阅读材料,再解方程组.
解方程组 时,可由①得,③然后再将③代入②,得
,解得,从而进一步得 这种方法被称为“整体代入法”.
请用上述方法解方程组:
20.(7分)下图均为的正方形网格,每个小正方形的顶点称为格点,的顶点和点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图,并保留作图痕迹.
(1) 在图①中,将平移,使点与点重合,点,的对应点为点,,画出;
(2) 在图②中,画出,使与关于点成中心对称;
(3) 在图③中,画出将绕点顺时针旋转 得到的.
21.(8分)如图,在中,点是边上的一点,连结.
(1) 若 ,,求的度数;
(2) 若平分, , ,试说明:.
22.(9分)骑车佩戴安全头盔,可以保护头部,减少意外伤害,某商店经销进价分别为40元/个、30元/个的甲、乙两种安全头盔,下表是近两天的销售情况(进价、售价均保持不变,利润售价-进价)
时间 甲头盔销量(个) 乙头盔销量(个) 销售金额(元)
周一 10 10 950
周二 6 15 930
(1) 求甲、乙两种头盔的销售单价;
(2) 若该商店计划用不多于3 450元的资金再购进这两种头盔共100个,当销售完这100个头盔时,能否实现利润为1 250元的目标?若能,请给出相应的进货方案;若不能,请说明理由.
23.[2024·长春期末](10分)如图,在直线上顺次取,,三点,已知,,点,分别从,两点同时出发向点运动.当其中一动点到达点时,,同时停止运动.已知点的速度为每秒2个单位长度,点的速度为每秒1个单位长度,设运动时间为秒.
(1) 用含的式子表示线段的长度为________;
(2) 当为何值时,,两点重合?
(3) 若点为中点,点为中点.问:为何值时,的长度为5?
24.(12分)
(1) 【问题背景】小明在学习多边形时,把如图①所示的图形看成“8”字形,并得出如下结论:,请你说明理由.
(2) 【尝试应用】如图②,、分别平分、,若 , ,求的度数.
小明结合(1)中的结论并利用方程思想轻松解答如下:
解:由、分别平分、,可设,,
由(1)的结论,得
…
请你帮小明把求解过程补充完整.
(3) 【拓展延伸】如图③,已知 , ,,,请利用上述结论或方法直接写出的度数.(用含 , 的代数式表示)
【参考答案】
一、选择题(本大题共8小题,每小题3分,共24分)
1.B
2.C
3.A
4.B
5.D
6.B
7.D
8.C
[解析]点拨:设每个小长方形的长为,宽为,
由题意得
解得
则每个小长方形的面积为.
二、填空题(本大题共6小题,每小题3分,共18分)
9.
10.0,1,2
11.
12.4
[解析]思路点睛:根据平移的性质得到,然后根据线段中点的定义得到,即可计算得到答案.
13.
14. 或
[解析]点拨:如图①所示,当 时,
是的角平分线, ,
,
;
如图②,当 时,
同理可得 .
是的高, ,
易知 ,
.
综上所述,的度数为 或 .
三、解答题(本大题共10小题,共78分)
15.解:去括号,得,
移项,得,
合并同类项,得,
系数化为1,得.
解集在数轴上的表示如图.
16.解:去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得.
17.解:,得,
解得,
将代入①,得,
解得,
所以原方程组的解为
18.(1) 解:不等式的基本性质2
(2) 六; 系数化为1时两边同乘负数没有改变不等号方向
(3) 由不等式①,得.
解得.
由不等式②,得.
解得.
所以原不等式组正确的解集是.
19.解:
由①,得,③
将③代入②,得,
解得,
将代入③,得,
解得.
故原方程组的解为
20.(1) 解:如图①,即为所作.
(2) 如图②,即为所作.
(3) 如图③,即为所作.
21.(1) 解: ,,,
,
.
(2) , ,
.
平分,
,
,
即.
22.(1) 解:设甲种头盔的销售单价为元,乙种头盔的销售单价为元,
依题意得
解得
答:甲种头盔的销售单价为55元,乙种头盔的销售单价为40元.
(2) 不能.理由如下:设购进甲种头盔个,则购进乙种头盔个,依题意得
解不等式①,得,
解方程②,得,
不存在符合题意的的值,即当销售完这100个头盔时,不能实现利润为1 250元的目标.
23.(1)
(2) 解:由题意得,,,
当,两点重合时,,
,
解得,
当时,、两点重合.
(3) 由题意得,,,
点为中点,点为中点.
,,
.
当点在点的左边时,,
解得;
当点在点的右边时,,
解得,
当或50时,的长度为5.
24.(1) 解:在中, ,
在中, .
,
.
(2) ,得,
即,
.
(3) .
/
同课章节目录
