第6章 一次方程组 测试卷(含答案)华师版数学七年级下册(2024)
文档属性
| 名称 | 第6章 一次方程组 测试卷(含答案)华师版数学七年级下册(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 53.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 15:31:45 | ||
图片预览



文档简介
第6章 一次方程组
一、选择题(本大题共8小题,每小题3分,共24分)
1.[2024·长春开学考试]下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
2.[2024·吉林期末]下列四组数中,不是二元一次方程的解的是( )
A. B. C. D.
3.[2024·吉林长春期末]解方程组时,把②代入①,正确的是( )
A. B.
C. D.
4.已知,满足方程组则的值为( )
A. B. C.2 D.3
5.方程组 的解是( )
A. B. C. D.
6.一种饮料有大盒,小盒两种包装,5大盒和3小盒共有150瓶,2大盒和6小盒共有100瓶,大盒,小盒每盒各有多少瓶?设大盒每盒有瓶,小盒每盒有瓶,则可列方程组为( )
A. B.
C. D.
7.端午节前夕,某食品加工厂准备将生产的粽子装入A、B两种食品盒中,A种食品盒每盒装8个粽子,B种食品盒每盒装10个粽子,若要将200个粽子分别装入A、B两种食品盒中(两种食品盒均要使用并且装满),则不同的分装方式有( )
A.3种 B.4种 C.5种 D.6种
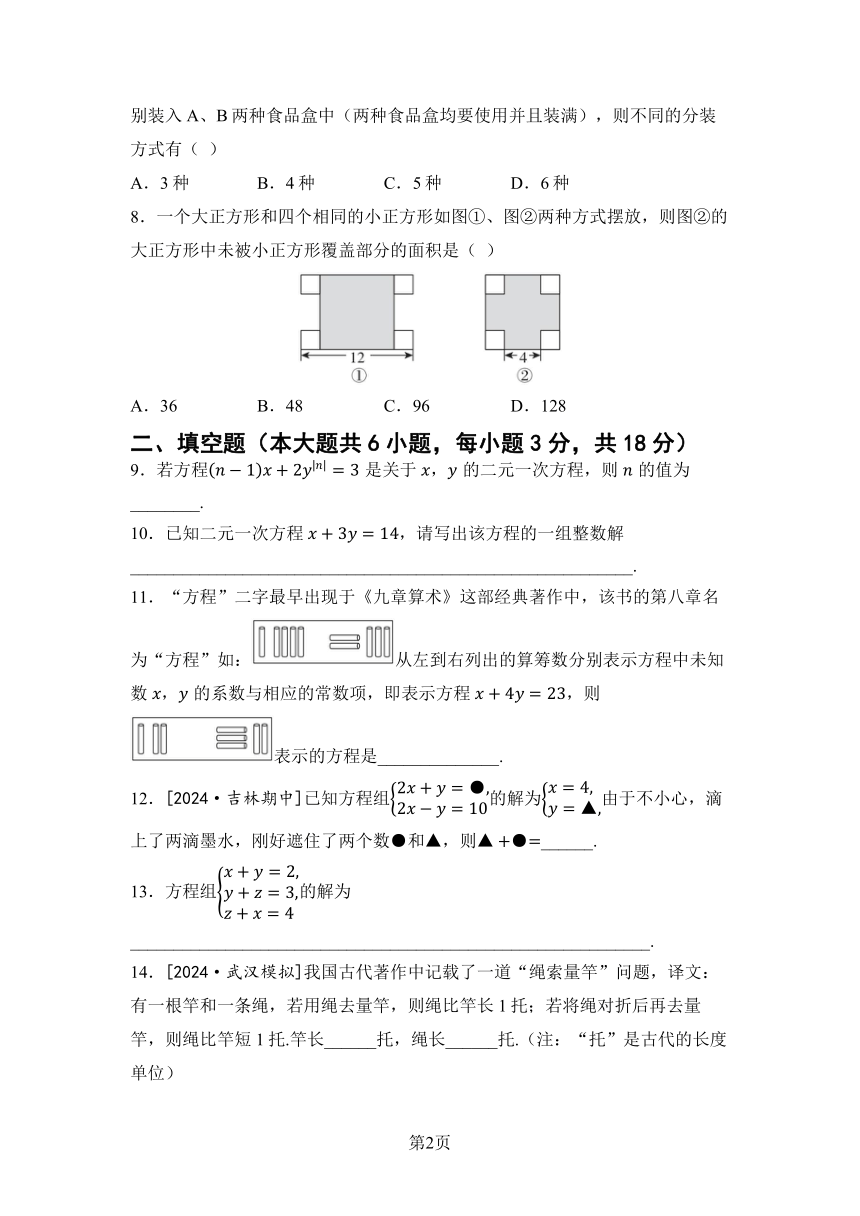
8.一个大正方形和四个相同的小正方形如图①、图②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是( )
A.36 B.48 C.96 D.128
二、填空题(本大题共6小题,每小题3分,共18分)
9.若方程是关于,的二元一次方程,则的值为________.
10.已知二元一次方程,请写出该方程的一组整数解 __________________________________________________________.
11.“方程”二字最早出现于《九章算术》这部经典著作中,该书的第八章名为“方程”如:从左到右列出的算筹数分别表示方程中未知数,的系数与相应的常数项,即表示方程,则表示的方程是______________.
12.[2024·吉林期中]已知方程组的解为由于不小心,滴上了两滴墨水,刚好遮住了两个数●和,则●______.
13.方程组的解为____________________________________________________________.
14.[2024·武汉模拟]我国古代著作中记载了一道“绳索量竿”问题,译文:有一根竿和一条绳,若用绳去量竿,则绳比竿长1托;若将绳对折后再去量竿,则绳比竿短1托.竿长______托,绳长______托.(注:“托”是古代的长度单位)
三、解答题(本大题共10小题,共78分)
15.(6分)解方程组:
(1)
(2)
(3)
16.(6分)已知,与,都是方程的解.
(1) 求与的值;
(2) 当时,求的值.
17.(6分)已知关于,的方程组的解互为相反数,求的值和这个方程组的解.
18.[2024·吉林期末](7分)我们定义一个关于非零常数,的新运算,规定:.例如:.若,,求,的值.
19.(7分)盲盒近来火爆,这种不确定的“盲抽”模式受到了年轻人的青睐.某商场计划采购潮玩盲盒和高品质精品盲盒这两种盲盒共500盒,这两种盲盒的进价如下表:
类型 进价(元/盒)
潮玩盲盒 20
高品质精品盲盒 68
若采购共用去14 800元,则两种盲盒各采购多少盒?
20.(7分)A、B两地相距,一辆慢车从A地开出,一辆快车从B地开出.如果两车同时相向而行,那么后相遇;如果两车同时同向(B到A的方向)而行,那么快车可追上慢车,求快车和慢车的速度各是多少?
21.[2024·长春模拟](8分)甲、乙两人同时解方程组甲看错了,求得的解为乙看错了,求得的解为求原方程组的正确的解.
22.(9分)“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆型车和1辆型车载满脐橙一次可运走;用1辆型车和2辆型车载满脐橙一次可运走,现有脐橙,计划同时租用型车辆,型车辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1) 1辆型车和1辆型车都载满脐橙一次可分别运送多少吨
(2) 请你帮该物流公司设计租车方案.
23.[2024·长春开学考试](10分)阅读理解:已知实数,满足①,,求 和 的值.仔细观察两个方程未知数的系数之间的关系,本题可以通过将两个方程进行加减或适当变形后进行加减,整体求得代数式的值,如:由 可得,由 可得.这样的解题思想就是通常所说的“整体思想”.
利用“整体思想”,解决下列问题:
(1) 已知二元一次方程组:则________,______;
(2) 买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,求购买5支铅笔、5块橡皮、5本日记本共需多少元?
(3) 对于有理数,,定义新运算:,其中,,是常数.已知,,求的值.
24.(12分) 根据以下信息,探索完成任务:
如何设计招聘方案?
素材1 某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.每名熟练工均能独立安装电动汽车,由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人,经过培训上岗可以独立进行安装.
素材2 调研部门发现:2名熟练工和3名新工人每月可安装14辆电动汽车;3名熟练工和2名新工人每月可安装16辆电动汽车.
素材3 工厂给安装电动汽车的每名熟练工每月发6 000元工资,每名新工人每月发3 600元工资.
问题解决
任务一:.分析数量关系
每名熟练工和每名新工人每月分别可以安装多少辆电动汽车?
任务二:.确定可行方案
如果工厂招聘 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种抽调熟练工和招聘新工人的方案?
任务三:.选取最优方案
在上述方案中,为了节省成本,应该招聘新工人______名.(直接写出答案)
【参考答案】
一、选择题(本大题共8小题,每小题3分,共24分)
1.B 2.D 3.A 4.C 5.D 6.D 7.B 8.B
二、填空题(本大题共6小题,每小题3分,共18分)
9.
[解析]点拨:由题意,得且,
所以.
10.(答案不唯一)
11.
12.4
13.
14.3; 4
三、解答题(本大题共10小题,共78分)
15.(1) 解:由①得,③
把③代入②,得,解得,
把代入③,得,
所以原方程组的解是
(2) 由①得,③
,得,
解得,
把代入②,得,
解得,
所以原方程组的解是
(3) ,得,解得,
由②得,④
把和④代入①,得,解得,
把,代入④,得,
所以原方程组的解是
16.(1) 解:根据题意,得
解得
(2) 由(1)可得,
将代入,得.
17.解:,得,即.
,得,即.
根据题意,得,即,
解得.
所以原方程组为解得
18.解:由题意可得
,得,解得.
将代入①,得,
解得.
,.
19.解:设采购潮玩盲盒盒,高品质精品盲盒盒,
由题意得解得
答:采购潮玩盲盒400盒,高品质精品盲盒100盒.
20.解:设快车和慢车的速度分别是和.
根据题意,得解得
答:快车和慢车的速度分别是和.
21.解:根据题意,
把代入①中,得,解得,
把代入②中,得,解得,
故原方程组为
,得,解得.
把代入②中,得,解得,故原方程组的正确的解为
22.(1) 解:设1辆型车载满脐橙一次可运送,1辆型车载满脐橙一次可运送,
依题意,得
解得
解:1辆型车载满脐橙一次可运送,1辆型车载满脐橙一次可运送;
(2) 依题意,得,
又,均为正整数,
或或
一共有3种租车方案:
方案一:租型车1辆,型车7辆;
方案二:租型车5辆,型车4辆;
方案三:租型车9辆,型车1辆.
23.(1) ; 5
(2) 解:设每支铅笔元,每块橡皮元,每本日记本元,由题意,得
,得,
所以.
答:购买5支铅笔、5块橡皮、5本日记本共需30元.
(3) 由题意,得
,得,
所以.
24.任务一: 解:设每名熟练工每月可以安装辆电动汽车,每名新工人每月可以安装辆电动汽车,
由题意,得解得
答:每名熟练工每月可以安装4辆电动汽车,每名新工人每月可以安装2辆电动汽车.
任务二: 设抽调熟练工名,
由题意,得,整理,得.
因为,为整数,且,所以或
所以有两种方案:①抽调熟练工3名,招聘新工人4名;
②抽调熟练工4名,招聘新工人2名.
任务三: 2
第页
一、选择题(本大题共8小题,每小题3分,共24分)
1.[2024·长春开学考试]下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
2.[2024·吉林期末]下列四组数中,不是二元一次方程的解的是( )
A. B. C. D.
3.[2024·吉林长春期末]解方程组时,把②代入①,正确的是( )
A. B.
C. D.
4.已知,满足方程组则的值为( )
A. B. C.2 D.3
5.方程组 的解是( )
A. B. C. D.
6.一种饮料有大盒,小盒两种包装,5大盒和3小盒共有150瓶,2大盒和6小盒共有100瓶,大盒,小盒每盒各有多少瓶?设大盒每盒有瓶,小盒每盒有瓶,则可列方程组为( )
A. B.
C. D.
7.端午节前夕,某食品加工厂准备将生产的粽子装入A、B两种食品盒中,A种食品盒每盒装8个粽子,B种食品盒每盒装10个粽子,若要将200个粽子分别装入A、B两种食品盒中(两种食品盒均要使用并且装满),则不同的分装方式有( )
A.3种 B.4种 C.5种 D.6种
8.一个大正方形和四个相同的小正方形如图①、图②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是( )
A.36 B.48 C.96 D.128
二、填空题(本大题共6小题,每小题3分,共18分)
9.若方程是关于,的二元一次方程,则的值为________.
10.已知二元一次方程,请写出该方程的一组整数解 __________________________________________________________.
11.“方程”二字最早出现于《九章算术》这部经典著作中,该书的第八章名为“方程”如:从左到右列出的算筹数分别表示方程中未知数,的系数与相应的常数项,即表示方程,则表示的方程是______________.
12.[2024·吉林期中]已知方程组的解为由于不小心,滴上了两滴墨水,刚好遮住了两个数●和,则●______.
13.方程组的解为____________________________________________________________.
14.[2024·武汉模拟]我国古代著作中记载了一道“绳索量竿”问题,译文:有一根竿和一条绳,若用绳去量竿,则绳比竿长1托;若将绳对折后再去量竿,则绳比竿短1托.竿长______托,绳长______托.(注:“托”是古代的长度单位)
三、解答题(本大题共10小题,共78分)
15.(6分)解方程组:
(1)
(2)
(3)
16.(6分)已知,与,都是方程的解.
(1) 求与的值;
(2) 当时,求的值.
17.(6分)已知关于,的方程组的解互为相反数,求的值和这个方程组的解.
18.[2024·吉林期末](7分)我们定义一个关于非零常数,的新运算,规定:.例如:.若,,求,的值.
19.(7分)盲盒近来火爆,这种不确定的“盲抽”模式受到了年轻人的青睐.某商场计划采购潮玩盲盒和高品质精品盲盒这两种盲盒共500盒,这两种盲盒的进价如下表:
类型 进价(元/盒)
潮玩盲盒 20
高品质精品盲盒 68
若采购共用去14 800元,则两种盲盒各采购多少盒?
20.(7分)A、B两地相距,一辆慢车从A地开出,一辆快车从B地开出.如果两车同时相向而行,那么后相遇;如果两车同时同向(B到A的方向)而行,那么快车可追上慢车,求快车和慢车的速度各是多少?
21.[2024·长春模拟](8分)甲、乙两人同时解方程组甲看错了,求得的解为乙看错了,求得的解为求原方程组的正确的解.
22.(9分)“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆型车和1辆型车载满脐橙一次可运走;用1辆型车和2辆型车载满脐橙一次可运走,现有脐橙,计划同时租用型车辆,型车辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1) 1辆型车和1辆型车都载满脐橙一次可分别运送多少吨
(2) 请你帮该物流公司设计租车方案.
23.[2024·长春开学考试](10分)阅读理解:已知实数,满足①,,求 和 的值.仔细观察两个方程未知数的系数之间的关系,本题可以通过将两个方程进行加减或适当变形后进行加减,整体求得代数式的值,如:由 可得,由 可得.这样的解题思想就是通常所说的“整体思想”.
利用“整体思想”,解决下列问题:
(1) 已知二元一次方程组:则________,______;
(2) 买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,求购买5支铅笔、5块橡皮、5本日记本共需多少元?
(3) 对于有理数,,定义新运算:,其中,,是常数.已知,,求的值.
24.(12分) 根据以下信息,探索完成任务:
如何设计招聘方案?
素材1 某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.每名熟练工均能独立安装电动汽车,由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人,经过培训上岗可以独立进行安装.
素材2 调研部门发现:2名熟练工和3名新工人每月可安装14辆电动汽车;3名熟练工和2名新工人每月可安装16辆电动汽车.
素材3 工厂给安装电动汽车的每名熟练工每月发6 000元工资,每名新工人每月发3 600元工资.
问题解决
任务一:.分析数量关系
每名熟练工和每名新工人每月分别可以安装多少辆电动汽车?
任务二:.确定可行方案
如果工厂招聘 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种抽调熟练工和招聘新工人的方案?
任务三:.选取最优方案
在上述方案中,为了节省成本,应该招聘新工人______名.(直接写出答案)
【参考答案】
一、选择题(本大题共8小题,每小题3分,共24分)
1.B 2.D 3.A 4.C 5.D 6.D 7.B 8.B
二、填空题(本大题共6小题,每小题3分,共18分)
9.
[解析]点拨:由题意,得且,
所以.
10.(答案不唯一)
11.
12.4
13.
14.3; 4
三、解答题(本大题共10小题,共78分)
15.(1) 解:由①得,③
把③代入②,得,解得,
把代入③,得,
所以原方程组的解是
(2) 由①得,③
,得,
解得,
把代入②,得,
解得,
所以原方程组的解是
(3) ,得,解得,
由②得,④
把和④代入①,得,解得,
把,代入④,得,
所以原方程组的解是
16.(1) 解:根据题意,得
解得
(2) 由(1)可得,
将代入,得.
17.解:,得,即.
,得,即.
根据题意,得,即,
解得.
所以原方程组为解得
18.解:由题意可得
,得,解得.
将代入①,得,
解得.
,.
19.解:设采购潮玩盲盒盒,高品质精品盲盒盒,
由题意得解得
答:采购潮玩盲盒400盒,高品质精品盲盒100盒.
20.解:设快车和慢车的速度分别是和.
根据题意,得解得
答:快车和慢车的速度分别是和.
21.解:根据题意,
把代入①中,得,解得,
把代入②中,得,解得,
故原方程组为
,得,解得.
把代入②中,得,解得,故原方程组的正确的解为
22.(1) 解:设1辆型车载满脐橙一次可运送,1辆型车载满脐橙一次可运送,
依题意,得
解得
解:1辆型车载满脐橙一次可运送,1辆型车载满脐橙一次可运送;
(2) 依题意,得,
又,均为正整数,
或或
一共有3种租车方案:
方案一:租型车1辆,型车7辆;
方案二:租型车5辆,型车4辆;
方案三:租型车9辆,型车1辆.
23.(1) ; 5
(2) 解:设每支铅笔元,每块橡皮元,每本日记本元,由题意,得
,得,
所以.
答:购买5支铅笔、5块橡皮、5本日记本共需30元.
(3) 由题意,得
,得,
所以.
24.任务一: 解:设每名熟练工每月可以安装辆电动汽车,每名新工人每月可以安装辆电动汽车,
由题意,得解得
答:每名熟练工每月可以安装4辆电动汽车,每名新工人每月可以安装2辆电动汽车.
任务二: 设抽调熟练工名,
由题意,得,整理,得.
因为,为整数,且,所以或
所以有两种方案:①抽调熟练工3名,招聘新工人4名;
②抽调熟练工4名,招聘新工人2名.
任务三: 2
第页
