第8章 三角形 测试卷(含答案)华师版数学七年级下册(2024)
文档属性
| 名称 | 第8章 三角形 测试卷(含答案)华师版数学七年级下册(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 224.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 15:33:44 | ||
图片预览




文档简介
第8章 三角形
一、选择题(本大题共8小题,每小题3分,共24分)
1.在中, , ,则的形状是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.无法确定
2.[2024·长春期末]以下列长度的各组线段为边,能组成三角形的是( )
A.、、 B.、、
C.、、 D.、、
3.如图,虚线部分是小刚作的辅助线,你认为线段( )
(第3题)
A.是边上的高 B.是边上的高
C.是边上的高 D.不是的高
4.[2024·长春中考改编]在剪纸活动中,小花同学想用一张长方形纸片剪出一个正五边形,其中正五边形的一条边与长方形的边重合,如图所示,则 的大小为( )
(第4题)
A. B. C. D.
5.[2024·长春期末]如图,将一张长方形纸片与含 角的三角尺摆放在一起,若 ,则的度数是( )
(第5题)
A. B. C. D.
6.[2024·长春期末]李明同学在学完用正多边形铺设地面这节课之后,建议爸爸为他家房屋地面进行装修.爸爸选中了一种漂亮的正八边形地砖,他告诉爸爸,只用一种正八边形地砖是不能铺满地面的,需要与另外一种边长相等的正多边形地砖组合使用,你认为要使地面铺满,李明应建议爸爸选择另一种地砖的形状为( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
7.如图,已知,是它的一个外角,为上一点,点在边的延长线上,连结,则下列结论中不一定正确的是( )
(第7题)
A. B. C. D.
8.如图,( )
(第8题)
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
9.[2024·长春开学考试]三角形在日常生活和生产中有很多应用,如家用梯子(如图)的设计中都有三角形结构,这样做的依据是三角形具有________.
(第9题)
10.如图,已知直线, , ,则____________.
(第10题)
11.[2024·长春模拟]一个多边形的内角和等于它的外角和的两倍,那么这个多边形是__边形.
12.已知三角形的三边长分别为1,,3,则化简的结果为______.
13.如图,,分别是的一条高和一条中线.若,,则______.
(第13题)
14.[2024·苏州期末]如图,在中, ,,,点是的中点,动点从点出发,以每秒的速度沿运动,若设点运动时间是秒,那么当____________时,的面积等于.
(第14题)
三、解答题(本大题共10小题,共78分)
15.(6分)如图,在中,平分, , .求和的度数.
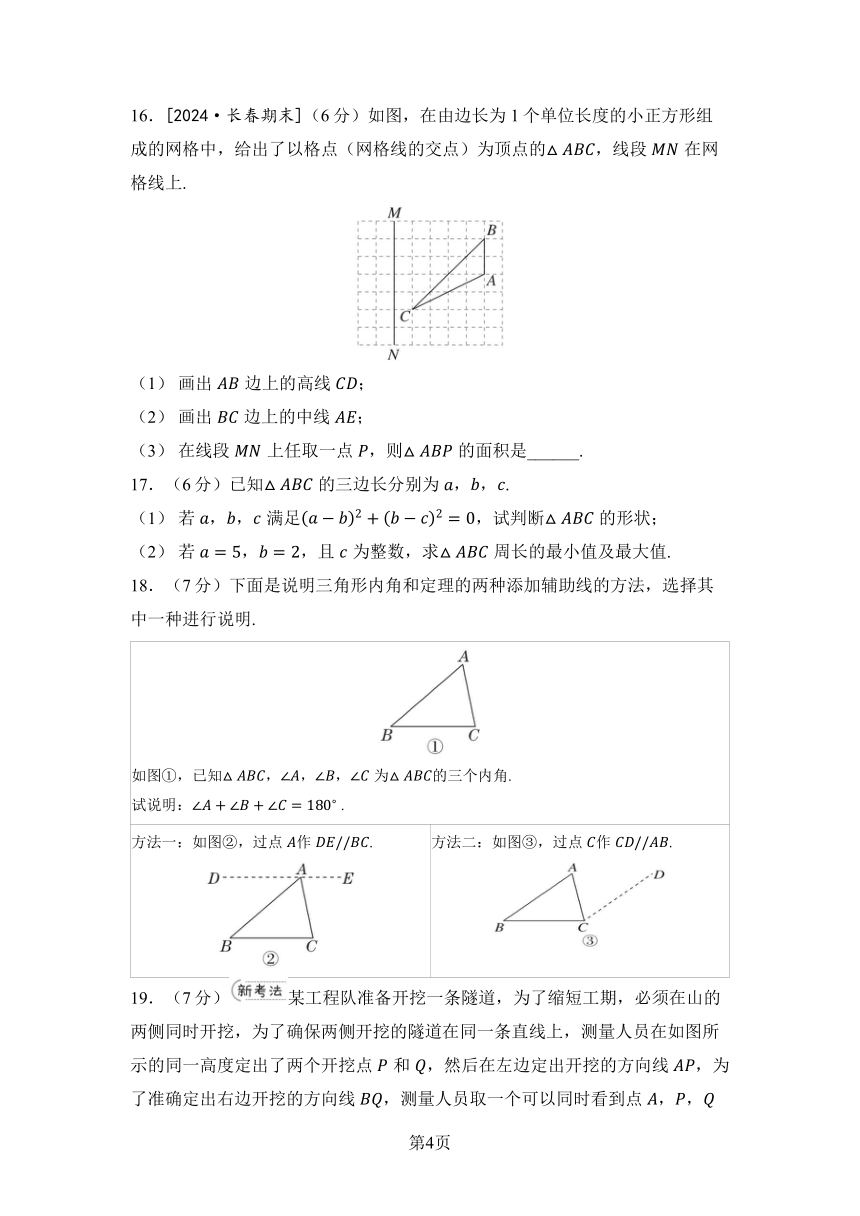
16.[2024·长春期末](6分)如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的,线段在网格线上.
(1) 画出边上的高线;
(2) 画出边上的中线;
(3) 在线段上任取一点,则的面积是______.
17.(6分)已知的三边长分别为,,.
(1) 若,,满足,试判断的形状;
(2) 若,,且为整数,求周长的最小值及最大值.
18.(7分)下面是说明三角形内角和定理的两种添加辅助线的方法,选择其中一种进行说明.
如图①,已知,,,为 的三个内角. 试说明: .
方法一:如图②,过点 作. 方法二:如图③,过点 作.
19.(7分)某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图所示的同一高度定出了两个开挖点和,然后在左边定出开挖的方向线,为了准确定出右边开挖的方向线,测量人员取一个可以同时看到点,,的点,测得 , ,那么应等于多少度才能确保与在同一条直线上?
20.(7分)如图,在中,为的平分线,为边上的高,与交于点, , .
(1) __ ;
(2) 求的度数.
21.(8分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大 .
(1) 求这个多边形的边数;
(2) 若将这个多边形剪去一个角,剩下多边形的内角和为多少?
22.(9分)已知,是直角三角形,且 ,交于点,交于点.
(1) 当的位置如图①所示时,与的数量关系是______________________;
(2) 当的位置如图②所示时,试说明: ;
(3) 在(2)的条件下,若与交于点,且 , ,求的度数.
23.(10分)在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角时,就拼成了一个平面图形.
(1) 请根据下列图形,填写表中空格.
正多边形边数 3 4 5 6 …
正多边形每个内角的度数 ________ ________ __________ __________ … ____________________
(2) 如果限于用如图所示的其中一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
(3) 从正三角形、正方形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形
24.(12分)在中,与的平分线相交于点.
(1) 如图①,若 ,则____ ;
(2) 如图②,作的外角,的平分线,交于点,试探索,之间的数量关系;
(3) 如图③,在图②的基础上延长,,交于点,若在中存在一个内角等于另一个内角的2倍,求的度数.
【参考答案】
一、选择题(本大题共8小题,每小题3分,共24分)
1.C 2.B 3.B 4.D 5.A 6.B 7.D 8.B
二、填空题(本大题共6小题,每小题3分,共18分)
9.稳定性
10.
11.六
12.2
[解析]点拨:由三角形的三边关系可得,所以.所以.
13.5
[解析]点拨:是的一条中线,,,.
14.2或
[解析]点拨:,点是的中点,
.
当点在线段上时,如图①所示,,
,
,
由,得.
当点在线段上时,如图②所示,易得,
,
由,得.
三、解答题(本大题共10小题,共78分)
15.解:平分, ,
.
, .
是的一个外角,
.
16.(1) 解:边上的高线如图所示.
(2) 边上的中线如图所示.
(3) 5
17.(1) 解:,
,,,
是等边三角形.
(2) ,,
,即.
为整数,,5,6.
当时,的周长最小,最小值为;
当时,的周长最大,最大值为.
18.解:选择方法一,,
,.
,
.
选择方法二,,
,.
.(选择一种方法即可)
19.解:当点、、、共线,即点、在的边上时,两侧开挖的隧道在同一条直线上.
,
,
即应等于 才能确保与在同一条直线上.
20.(1) 40
(2) 解:由(1)易知 .
为边上的高,
,
,
.
21.(1) 解:设每一个内角的相邻外角为,则每一个内角为 ,所以 ,解得 ,
,
所以这个多边形的边数为9.
(2) 分以下三种情况:
①剪去一个角后,多边形的边数减少1条,即变成八边形,则剩下多边形的内角和为 ;
②剪去一个角后,多边形的边数不变,即还是九边形,
则剩下多边形的内角和为 ;
③剪去一个角后,多边形的边数增加1条,即变成十边形,则剩下多边形的内角和为 .
所以若将这个多边形剪去一个角,剩下多边形的内角和为 或 或 .
22.(1)
(2) 解:设交于点.
,.
,,
.
(3) , ,
.
, .
,
.
23.(1) ; ; ; ;
(2) 解:设这种正多边形的边数为,当为正整数时,求出的的值符合题意.
,
要使为正整数,则4为的倍数.
所以或2或4,所以或4或6.
所以正三角形、正方形、正六边形能镶嵌成一个平面图形.
(3) (答案不唯一)选正方形和正八边形,镶嵌成的平面图形如图所示.
正八边形每个内角的度数为 .
设在一个顶点周围有个正方形,个正八边形,
则,应是方程,
即的正整数解,
因为此方程的正整数解只有,一组,
所以正方形和正八边形共能镶嵌成一种平面图形.
24.(1) 130
(2) 解:,的平分线交于点,
,,
.
, ,
,,
.
,
.
(3) 延长至,是的平分线,
易得是的平分线,
.
平分,.
,
,即.
又,.
.
在中存在一个内角等于另一个内角的2倍的情况分四种:
① ,则 ,
;
② ,则 ,
,
;
③,
,
, ,
;
④,则 ,
, .
综上所述,的度数是 或 或 .
第页
一、选择题(本大题共8小题,每小题3分,共24分)
1.在中, , ,则的形状是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.无法确定
2.[2024·长春期末]以下列长度的各组线段为边,能组成三角形的是( )
A.、、 B.、、
C.、、 D.、、
3.如图,虚线部分是小刚作的辅助线,你认为线段( )
(第3题)
A.是边上的高 B.是边上的高
C.是边上的高 D.不是的高
4.[2024·长春中考改编]在剪纸活动中,小花同学想用一张长方形纸片剪出一个正五边形,其中正五边形的一条边与长方形的边重合,如图所示,则 的大小为( )
(第4题)
A. B. C. D.
5.[2024·长春期末]如图,将一张长方形纸片与含 角的三角尺摆放在一起,若 ,则的度数是( )
(第5题)
A. B. C. D.
6.[2024·长春期末]李明同学在学完用正多边形铺设地面这节课之后,建议爸爸为他家房屋地面进行装修.爸爸选中了一种漂亮的正八边形地砖,他告诉爸爸,只用一种正八边形地砖是不能铺满地面的,需要与另外一种边长相等的正多边形地砖组合使用,你认为要使地面铺满,李明应建议爸爸选择另一种地砖的形状为( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
7.如图,已知,是它的一个外角,为上一点,点在边的延长线上,连结,则下列结论中不一定正确的是( )
(第7题)
A. B. C. D.
8.如图,( )
(第8题)
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
9.[2024·长春开学考试]三角形在日常生活和生产中有很多应用,如家用梯子(如图)的设计中都有三角形结构,这样做的依据是三角形具有________.
(第9题)
10.如图,已知直线, , ,则____________.
(第10题)
11.[2024·长春模拟]一个多边形的内角和等于它的外角和的两倍,那么这个多边形是__边形.
12.已知三角形的三边长分别为1,,3,则化简的结果为______.
13.如图,,分别是的一条高和一条中线.若,,则______.
(第13题)
14.[2024·苏州期末]如图,在中, ,,,点是的中点,动点从点出发,以每秒的速度沿运动,若设点运动时间是秒,那么当____________时,的面积等于.
(第14题)
三、解答题(本大题共10小题,共78分)
15.(6分)如图,在中,平分, , .求和的度数.
16.[2024·长春期末](6分)如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的,线段在网格线上.
(1) 画出边上的高线;
(2) 画出边上的中线;
(3) 在线段上任取一点,则的面积是______.
17.(6分)已知的三边长分别为,,.
(1) 若,,满足,试判断的形状;
(2) 若,,且为整数,求周长的最小值及最大值.
18.(7分)下面是说明三角形内角和定理的两种添加辅助线的方法,选择其中一种进行说明.
如图①,已知,,,为 的三个内角. 试说明: .
方法一:如图②,过点 作. 方法二:如图③,过点 作.
19.(7分)某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图所示的同一高度定出了两个开挖点和,然后在左边定出开挖的方向线,为了准确定出右边开挖的方向线,测量人员取一个可以同时看到点,,的点,测得 , ,那么应等于多少度才能确保与在同一条直线上?
20.(7分)如图,在中,为的平分线,为边上的高,与交于点, , .
(1) __ ;
(2) 求的度数.
21.(8分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大 .
(1) 求这个多边形的边数;
(2) 若将这个多边形剪去一个角,剩下多边形的内角和为多少?
22.(9分)已知,是直角三角形,且 ,交于点,交于点.
(1) 当的位置如图①所示时,与的数量关系是______________________;
(2) 当的位置如图②所示时,试说明: ;
(3) 在(2)的条件下,若与交于点,且 , ,求的度数.
23.(10分)在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角时,就拼成了一个平面图形.
(1) 请根据下列图形,填写表中空格.
正多边形边数 3 4 5 6 …
正多边形每个内角的度数 ________ ________ __________ __________ … ____________________
(2) 如果限于用如图所示的其中一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
(3) 从正三角形、正方形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形
24.(12分)在中,与的平分线相交于点.
(1) 如图①,若 ,则____ ;
(2) 如图②,作的外角,的平分线,交于点,试探索,之间的数量关系;
(3) 如图③,在图②的基础上延长,,交于点,若在中存在一个内角等于另一个内角的2倍,求的度数.
【参考答案】
一、选择题(本大题共8小题,每小题3分,共24分)
1.C 2.B 3.B 4.D 5.A 6.B 7.D 8.B
二、填空题(本大题共6小题,每小题3分,共18分)
9.稳定性
10.
11.六
12.2
[解析]点拨:由三角形的三边关系可得,所以.所以.
13.5
[解析]点拨:是的一条中线,,,.
14.2或
[解析]点拨:,点是的中点,
.
当点在线段上时,如图①所示,,
,
,
由,得.
当点在线段上时,如图②所示,易得,
,
由,得.
三、解答题(本大题共10小题,共78分)
15.解:平分, ,
.
, .
是的一个外角,
.
16.(1) 解:边上的高线如图所示.
(2) 边上的中线如图所示.
(3) 5
17.(1) 解:,
,,,
是等边三角形.
(2) ,,
,即.
为整数,,5,6.
当时,的周长最小,最小值为;
当时,的周长最大,最大值为.
18.解:选择方法一,,
,.
,
.
选择方法二,,
,.
.(选择一种方法即可)
19.解:当点、、、共线,即点、在的边上时,两侧开挖的隧道在同一条直线上.
,
,
即应等于 才能确保与在同一条直线上.
20.(1) 40
(2) 解:由(1)易知 .
为边上的高,
,
,
.
21.(1) 解:设每一个内角的相邻外角为,则每一个内角为 ,所以 ,解得 ,
,
所以这个多边形的边数为9.
(2) 分以下三种情况:
①剪去一个角后,多边形的边数减少1条,即变成八边形,则剩下多边形的内角和为 ;
②剪去一个角后,多边形的边数不变,即还是九边形,
则剩下多边形的内角和为 ;
③剪去一个角后,多边形的边数增加1条,即变成十边形,则剩下多边形的内角和为 .
所以若将这个多边形剪去一个角,剩下多边形的内角和为 或 或 .
22.(1)
(2) 解:设交于点.
,.
,,
.
(3) , ,
.
, .
,
.
23.(1) ; ; ; ;
(2) 解:设这种正多边形的边数为,当为正整数时,求出的的值符合题意.
,
要使为正整数,则4为的倍数.
所以或2或4,所以或4或6.
所以正三角形、正方形、正六边形能镶嵌成一个平面图形.
(3) (答案不唯一)选正方形和正八边形,镶嵌成的平面图形如图所示.
正八边形每个内角的度数为 .
设在一个顶点周围有个正方形,个正八边形,
则,应是方程,
即的正整数解,
因为此方程的正整数解只有,一组,
所以正方形和正八边形共能镶嵌成一种平面图形.
24.(1) 130
(2) 解:,的平分线交于点,
,,
.
, ,
,,
.
,
.
(3) 延长至,是的平分线,
易得是的平分线,
.
平分,.
,
,即.
又,.
.
在中存在一个内角等于另一个内角的2倍的情况分四种:
① ,则 ,
;
② ,则 ,
,
;
③,
,
, ,
;
④,则 ,
, .
综上所述,的度数是 或 或 .
第页
