第六章《特殊平行四边形》综合测试卷(含答案)
文档属性
| 名称 | 第六章《特殊平行四边形》综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 19.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-04 20:02:42 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章综合测试卷
时间: 60分钟 满分: 100分
一、选择题(每小题3分,共36分)
1.下列条件中,能使平行四边形 ABCD成为菱形的是 ( )
A. AC⊥BD B. AB⊥BC C. AB=CD
2.如图,菱形 ABCD 对角线交点与坐标原点O 重合,点 A(-2,5),则点 C 的坐标是 ( )
A.(5,-2) B.(2,-5) C.(2,5) D.(-2,-5)
3.已知菱形的周长为40,两条对角线之比3:4,则菱形面积为 ( )
A. 12 B. 24 C. 48 D. 96
4.下列是4 位同学所画的菱形,依据所标数据,不一定为菱形的是 ( )
5.小米同学在喝水时想到了这样一个问题:如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与AD的交点为E,当水杯底面AB 与水平面的夹角为 时,的大小为 ( )
第5题图 第6题图
6.如图,将矩形纸片ABCD沿对角线AC 对折,使得点B落在点E 处,CE交AD 于点 F,若CE平分∠ACD,AF=3,则 EF的长是 ( )
B.
7.如图,正方形ABCD的边长为4,菱形 BEDF 的边长为3,则菱形 BEDF 的面积为 ( )
B.8 C. 4
第7题图 第8题图
8.如图,在矩形ABCD中,对角线AC与BD 相交于点O,点E在AC 上,CE=BC,BE的延长线交AD 于点 F,若∠ACB=36°,连接OF,则下列结论正确的是 ( )
A. BF=BC B. BF=CD C. OF⊥BD D. OE=2AE
9.如图,在正方形ABCD中,点 E,F 分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于 ( )
A. 2α B. 90°-2α C. 45°-α D. 90°-α
第9题图 第10题图
10.如图,在正方形ABCD中,O为对角线AC 的中点,E为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE的平分线交于点F,连接OF,若AB=2,则OF的长度为 ( )
A. 2 B. C. 1
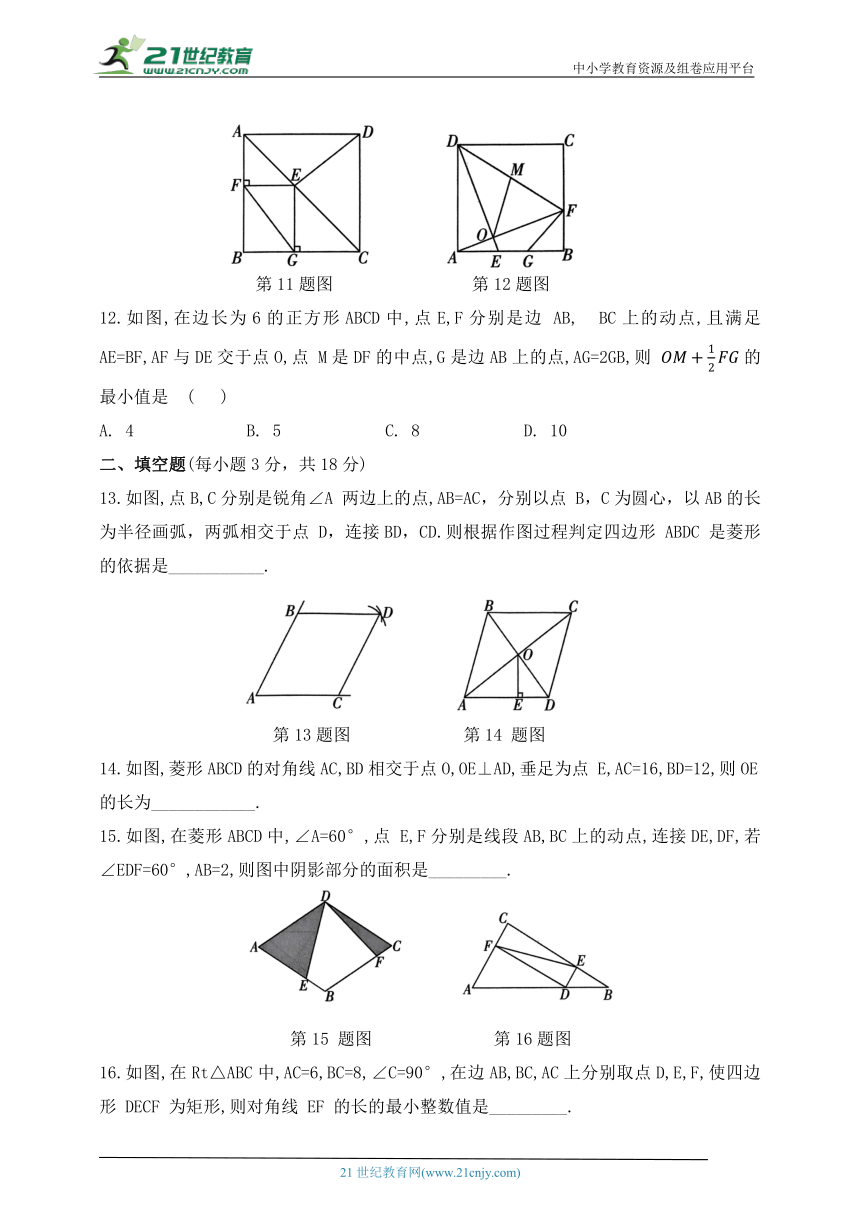
11.如图,在正方形 ABCD中,AB=4,E为对角线AC 上与A,C不重合的一个动点,过点E作EF⊥AB于点 F,EG⊥BC于点G, 连接DE,FG,下列结论:①DE=FG ②DE⊥FG ③∠BFG=∠ADE ④FG 的最小值为3.其中正确的结论有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
第11题图 第12题图
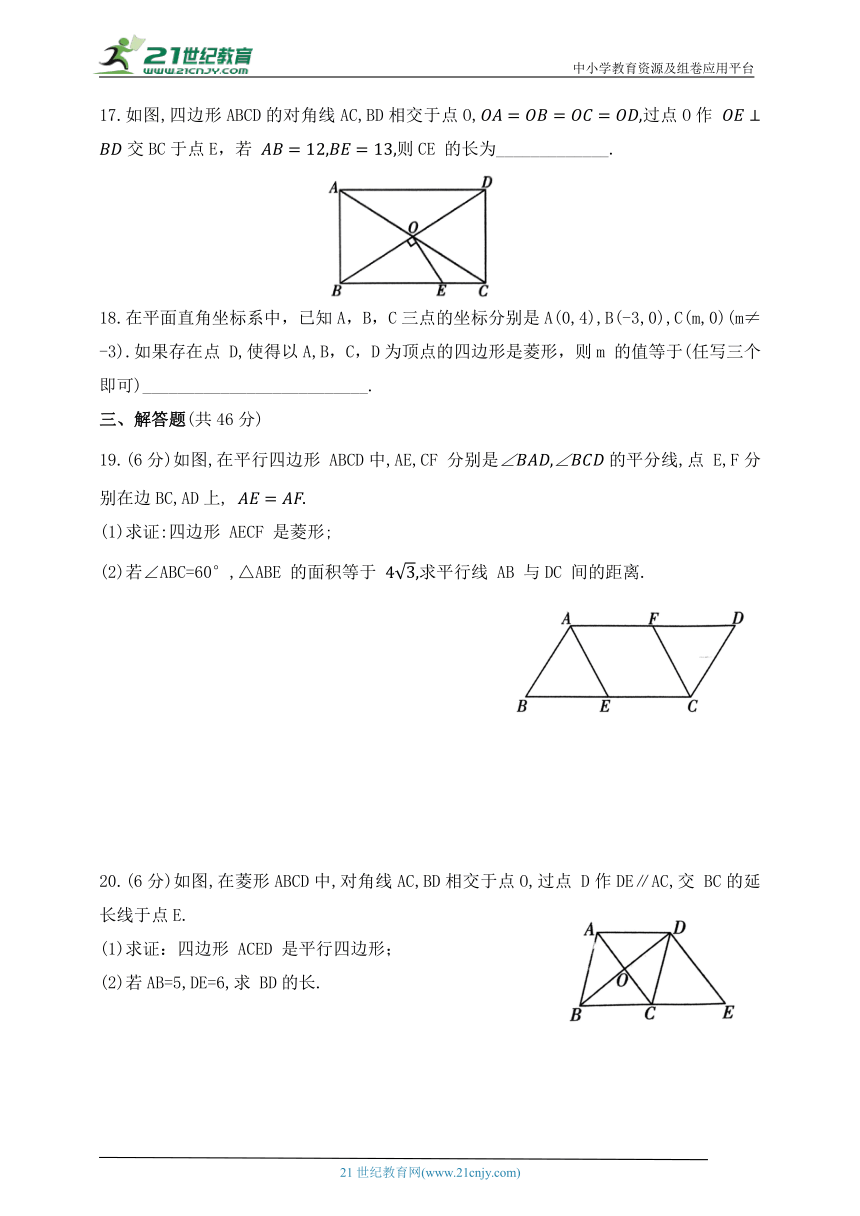
12.如图,在边长为6的正方形ABCD中,点E,F分别是边 AB, BC上的动点,且满足AE=BF,AF与DE交于点O,点 M是DF的中点,G是边AB上的点,AG=2GB,则 的最小值是 ( )
A. 4 B. 5 C. 8 D. 10
二、填空题(每小题3分,共18分)
13.如图,点B,C分别是锐角∠A 两边上的点,AB=AC,分别以点 B,C为圆心,以AB的长为半径画弧,两弧相交于点 D,连接BD,CD.则根据作图过程判定四边形 ABDC 是菱形的依据是___________.
第13题图 第14 题图
14.如图,菱形ABCD的对角线AC,BD相交于点O,OE⊥AD,垂足为点 E,AC=16,BD=12,则OE的长为____________.
15.如图,在菱形ABCD中,∠A=60°,点 E,F分别是线段AB,BC上的动点,连接DE,DF,若 ∠EDF=60°,AB=2,则图中阴影部分的面积是_________.
第15 题图 第16题图
16.如图,在Rt△ABC中,AC=6,BC=8,∠C=90°,在边AB,BC,AC上分别取点D,E,F,使四边形 DECF 为矩形,则对角线 EF 的长的最小整数值是_________.
17.如图,四边形ABCD的对角线AC,BD相交于点O,过点O作 交BC于点E,若 则CE 的长为_____________.
18.在平面直角坐标系中,已知A,B,C三点的坐标分别是A(0,4),B(-3,0),C(m,0)(m≠-3).如果存在点 D,使得以A,B,C,D为顶点的四边形是菱形,则m 的值等于(任写三个即可)__________________________.
三、解答题(共46分)
19.(6分)如图,在平行四边形 ABCD中,AE,CF 分别是的平分线,点 E,F分别在边BC,AD上,
(1)求证:四边形 AECF 是菱形;
(2)若∠ABC=60°,△ABE 的面积等于 求平行线 AB 与DC 间的距离.
20.(6分)如图,在菱形ABCD中,对角线AC,BD相交于点O,过点 D作DE∥AC,交 BC的延长线于点E.
(1)求证:四边形 ACED 是平行四边形;
(2)若AB=5,DE=6,求 BD的长.
21.(6分)如图,在矩形ABCD中,点E是BC 边上一点, 于点F.
(1)求证:
(2)若 求 BC 的长.
22.(6分)“三等分一个任意角”是数学史上一个著名问题.今天,人们已经知道,仅用圆规和直尺是不可能作出的.在探索中,有人曾利用过如图所示的图形,其中,ABCD是矩形,F是DA 延长线上一点,G是CF 上一点,并且
(1)求证:∠ACB=3∠ECB;
(2)若∠F=15°,矩形 ABCD面积为4,请直接写出 的周长.
23.(6分)在 中,AB=AC,点 D 为射线BC 上一动点(点 D 不与B,C重合),以AD为边作菱形ADEF,使 连接CF.
(1)如图1,当点 D 在线段BC上时,求证:BD=CF;
(2)如图2,当点D 在线段BC 的延长线上时,求证:BD=CF.
24.(8分)如图,四边形 ABCD 是菱形,过点A作BC,垂足分别为点 E,F,AE,AF 分别交BD 于点G,H.
(1)求证:
(2)延长AF,BC相交于点 P,当 时,求证:
25.(8分)如图,在正方形ABCD 中, E 是对角线AC上一动点,连接DE,作 EF⊥DE 交边 BC 或边 BC 的延长线于点F,以 DE 和EF 为邻边构造矩形DEFG,连接CG.
(1)若点 E 到边 BC 的距离为3,则它到边 DC 的距离为_________;
(2)求证:矩形 DEFG 是正方形;
(3)线段 AE 和线段CG.的数量关系是_________,位置关系是_________.
参考答案
1. A 2. B 3. D 4. B 5. C 6. A 7. D 8. C 9. A
10. D 解析:如图,连接AF,
∵四边形ABCD 是正方形,∴AB=BE=BC,∠ABC=90°,
∴∠BEC=∠BCE,∴∠EBC=180°-2∠BEC,∴∠ABE=∠ABC-∠EBC=2∠BEC-90°,
∵BF平分∠ABE, 45°,
∴∠BFE=∠BEC-∠EBF=45°,
在△BAF与△BEF中, ∴△BAF≌△BEF(SAS),
∴∠BFE=∠BFA=45°,∴∠AFC=∠BFA+∠BFE=90°,
∵O为对角线AC 的中点,
11. C
12. B 解析:∵四边形 ABCD是正方形, ∴AD=AB,∠DAB=∠ABC=90°,
又∵AE=BF,∴△ADE≌△BAF(SAS),∴∠ADE=∠BAF,
∴∠DOF =∠ADO+∠DAO=∠BAF+∠DAO=∠DAB=90°,
∵点 M 是 DF 的中点,
如图所示,在 AB 延长线上截取BH=BG,连接FH,
∵∠FBG=∠FBH=90°,FB=FB,BG=BH,∴△FBG≌△FBH(SAS),
∴FH=FG,
∴当H,D,F三点共线时,DF+HF有最小值,即此时 有最小值,最小值即为DH的长的一半,
∵AG=2GB,AB=6,∴BH=BG=2,∴AH=8,
在 Rt△ADH 中,由勾股定理得 DH = 的最小值为5.
13.四边相等的四边形是菱形 16. 5 17. 5
18. 3或-8或2或 (任写3个即可)
解析:如图1所示,
∵四边形ABDC 是菱形,∴点 B 与点 C 关于 AD 对称,AD 在 y轴上,
∴点C的坐标为(3,0),∴m的值等于3;
如图2所示,
∵四边形 ABCD 是菱形,
∴C点坐标为( ∴m的值等于
如图3所示,
∵四边形 ABCD 是菱形,
∴C点坐标为(2,0),∴m的值等于2;
如图4所示,
四边形 ADBC是菱形,
即 解得
综上所述,m的值等于3或 或2或
19.解:(1)证明:∵四边形 ABCD是平行四边形, ∥
∵AE,CF 分别是 的平分线,
∥
∥∴四边形 AECF 是平行四边形.
∵AE=AF,∴四边形AECF 是菱形;
(2)连接AC,
∵四边形 ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠AEB,
∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=EB,
∵∠ABC=60°,∴△ABE 是等边三角形,∴∠BAE=∠AEB=∠ABE=60°,
∵△ABE的面积等于 ∴AB=4,即AB=AE=EB=4,
由(1),得四边形 AECF 是菱形,∴AE=CE=4,∴∠EAC=∠ECA,
∵∠AEB 是△AEC的一个外角,∴∠AEB=∠EAC+∠ECA=60°,∴∠EAC=∠ECA=30°,
∴∠BAC=∠BAE+∠EAC=90°,即AC⊥AB,
由勾股定理得
即平行线 AB 与DC间的距离是
20.解:(1)证明:∵四边形 ABCD 是菱形,∴AD∥BC,即AD∥CE,
∵AC∥DE,∴四边形 ACED 是平行四边形;
(2)∵由(1),得四边形 ACED 是平行四边形,∴AC=DE=6,AC∥DE,
∵四边形ABCD为菱形,∴AB=AD=BC=5,AC⊥BD,∴BE=BC+CE=BC+AD=5+5=10,
∵AC∥DE,∴BD⊥DE,∴∠BDE=90°,
在 Rt△BDE 中,由勾股定理,得 BD = ∴BD的长为8.
21.解:(1)证明:∵四边形 ABCD为矩形,∴AD∥BC,∠B=90°,∴∠FAD=∠BEA.
∵DF⊥AE,∴∠DFA=90°=∠B.
在△ABE 和△DFA中, ∴△ABE≌△DFA(AAS),∴AB=DF;
(2)∵四边形ABCD 是矩形,∴BC=AD,∠B=90°,
设BC=x,则AD=BC=AE=x,BE=x-4,
解得x=10,∴BC=10.
22.解:(1)证明:∵∠GAF=∠F,∴∠AGC=∠F+∠GAF=2∠F,
∵∠ACG=∠AGC,∴∠ACG=2∠F,
∵四边形 ABCD是矩形,∴AD∥BC,∴∠ECB=∠F,
∴∠ACB=∠ACG+∠BCE=3∠F,即∠ACB=3∠ECB;
(2)∵∠F=15°,∴∠ACB=3×15°=45°=∠CAB,∴AB=BC,
又∵四边形ABCD 是矩形,∴四边形ABCD 是正方形,
∵正方形 ABCD面积为4,
∴△ABC的周长
23.证明:(1)∵四边形ADEF 是菱形,∴AD=AF,
∵∠BAC=∠DAF,∴∠BAD=∠CAF,
∵AB=AC,∴△BAD≌△CAF(SAS),∴BD=CF;
(2)∵四边形ADEF 是菱形,∴AD=AF,
∵∠BAC=∠DAF,∴∠BAD=∠CAF,
∵AB=AC,∴△BAD≌△CAF(SAS),∴BD=CF.
24.证明:(1)∵四边形ABCD 是菱形,∴AB=AD,AB∥CD,AD∥BC,∴∠ABD=∠ADB,
∵AE⊥BC,AF⊥CD,∴AE⊥AD,AF⊥AB,∴∠DAG=∠BAH=90°,
∴∠AHB=90°-∠ABD=90°-∠ADB=∠AGD,∴AH=AG;
(2)∵BG=GH,∴G是直角三角形ABH 斜边 BH 的中点,∴AG=BG=GH,
由(1),得AH=AG,∴AG=AH=GH,∴△AGH 是等边三角形,∴∠AHG=60°,
∴∠ABH=30°,∴∠ABC=60°,
∵AF⊥AB,∴∠BAP=90°,∴∠P=30°,
又∵AB∥CD,∴∠CFP=90°,∴CP=2CF,
如图,连接AC,
∵∠ADC=∠ABC=60°,AD=CD,∴△ADC是等边三角形,
∵AF⊥CD,∴CF=DF,
25.解:(1)如图,作EQ⊥BC于点Q,则EQ=3, EP⊥CD于点 P,
∵四边形ABCD是正方形,∴∠ACB=∠ACD=45°.
∵EP⊥CD,EQ⊥BC,∴EP=EQ=3.∴点 E 到边 DC 的距离为3,
故答案为:3;
(2)证明:∵∠EQC=∠EPC=∠BCD=90°,∴四边形 EQCP 是矩形.∴∠QEP=90°.
∵四边形 DEFG 是矩形,∴∠DEF=90°.∴∠DEP=∠FEQ.
∵∠EPD=∠EQF=90°,EP=EQ,∴△EPD≌△EQF(ASA).∴DE=FE,∴矩形 DEFG是正方形;
(3)∵四边形 DEFG是正方形,∴∠EDG=90°,DE=DG,
∵四边形ABCD是正方形,∴∠DAE=∠ACD=45°,∠ADC=90°,AD=CD,
∴∠ADC=∠EDG=90°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,∴∠ACD+∠DCG=90°,∴AE⊥CG,
综上可知,线段 AE 和线段CG 的数量关系是AE=CG,位置关系是AE⊥CG,
故答案为:AE=CG,AE⊥CG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章综合测试卷
时间: 60分钟 满分: 100分
一、选择题(每小题3分,共36分)
1.下列条件中,能使平行四边形 ABCD成为菱形的是 ( )
A. AC⊥BD B. AB⊥BC C. AB=CD
2.如图,菱形 ABCD 对角线交点与坐标原点O 重合,点 A(-2,5),则点 C 的坐标是 ( )
A.(5,-2) B.(2,-5) C.(2,5) D.(-2,-5)
3.已知菱形的周长为40,两条对角线之比3:4,则菱形面积为 ( )
A. 12 B. 24 C. 48 D. 96
4.下列是4 位同学所画的菱形,依据所标数据,不一定为菱形的是 ( )
5.小米同学在喝水时想到了这样一个问题:如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与AD的交点为E,当水杯底面AB 与水平面的夹角为 时,的大小为 ( )
第5题图 第6题图
6.如图,将矩形纸片ABCD沿对角线AC 对折,使得点B落在点E 处,CE交AD 于点 F,若CE平分∠ACD,AF=3,则 EF的长是 ( )
B.
7.如图,正方形ABCD的边长为4,菱形 BEDF 的边长为3,则菱形 BEDF 的面积为 ( )
B.8 C. 4
第7题图 第8题图
8.如图,在矩形ABCD中,对角线AC与BD 相交于点O,点E在AC 上,CE=BC,BE的延长线交AD 于点 F,若∠ACB=36°,连接OF,则下列结论正确的是 ( )
A. BF=BC B. BF=CD C. OF⊥BD D. OE=2AE
9.如图,在正方形ABCD中,点 E,F 分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于 ( )
A. 2α B. 90°-2α C. 45°-α D. 90°-α
第9题图 第10题图
10.如图,在正方形ABCD中,O为对角线AC 的中点,E为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE的平分线交于点F,连接OF,若AB=2,则OF的长度为 ( )
A. 2 B. C. 1
11.如图,在正方形 ABCD中,AB=4,E为对角线AC 上与A,C不重合的一个动点,过点E作EF⊥AB于点 F,EG⊥BC于点G, 连接DE,FG,下列结论:①DE=FG ②DE⊥FG ③∠BFG=∠ADE ④FG 的最小值为3.其中正确的结论有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
第11题图 第12题图
12.如图,在边长为6的正方形ABCD中,点E,F分别是边 AB, BC上的动点,且满足AE=BF,AF与DE交于点O,点 M是DF的中点,G是边AB上的点,AG=2GB,则 的最小值是 ( )
A. 4 B. 5 C. 8 D. 10
二、填空题(每小题3分,共18分)
13.如图,点B,C分别是锐角∠A 两边上的点,AB=AC,分别以点 B,C为圆心,以AB的长为半径画弧,两弧相交于点 D,连接BD,CD.则根据作图过程判定四边形 ABDC 是菱形的依据是___________.
第13题图 第14 题图
14.如图,菱形ABCD的对角线AC,BD相交于点O,OE⊥AD,垂足为点 E,AC=16,BD=12,则OE的长为____________.
15.如图,在菱形ABCD中,∠A=60°,点 E,F分别是线段AB,BC上的动点,连接DE,DF,若 ∠EDF=60°,AB=2,则图中阴影部分的面积是_________.
第15 题图 第16题图
16.如图,在Rt△ABC中,AC=6,BC=8,∠C=90°,在边AB,BC,AC上分别取点D,E,F,使四边形 DECF 为矩形,则对角线 EF 的长的最小整数值是_________.
17.如图,四边形ABCD的对角线AC,BD相交于点O,过点O作 交BC于点E,若 则CE 的长为_____________.
18.在平面直角坐标系中,已知A,B,C三点的坐标分别是A(0,4),B(-3,0),C(m,0)(m≠-3).如果存在点 D,使得以A,B,C,D为顶点的四边形是菱形,则m 的值等于(任写三个即可)__________________________.
三、解答题(共46分)
19.(6分)如图,在平行四边形 ABCD中,AE,CF 分别是的平分线,点 E,F分别在边BC,AD上,
(1)求证:四边形 AECF 是菱形;
(2)若∠ABC=60°,△ABE 的面积等于 求平行线 AB 与DC 间的距离.
20.(6分)如图,在菱形ABCD中,对角线AC,BD相交于点O,过点 D作DE∥AC,交 BC的延长线于点E.
(1)求证:四边形 ACED 是平行四边形;
(2)若AB=5,DE=6,求 BD的长.
21.(6分)如图,在矩形ABCD中,点E是BC 边上一点, 于点F.
(1)求证:
(2)若 求 BC 的长.
22.(6分)“三等分一个任意角”是数学史上一个著名问题.今天,人们已经知道,仅用圆规和直尺是不可能作出的.在探索中,有人曾利用过如图所示的图形,其中,ABCD是矩形,F是DA 延长线上一点,G是CF 上一点,并且
(1)求证:∠ACB=3∠ECB;
(2)若∠F=15°,矩形 ABCD面积为4,请直接写出 的周长.
23.(6分)在 中,AB=AC,点 D 为射线BC 上一动点(点 D 不与B,C重合),以AD为边作菱形ADEF,使 连接CF.
(1)如图1,当点 D 在线段BC上时,求证:BD=CF;
(2)如图2,当点D 在线段BC 的延长线上时,求证:BD=CF.
24.(8分)如图,四边形 ABCD 是菱形,过点A作BC,垂足分别为点 E,F,AE,AF 分别交BD 于点G,H.
(1)求证:
(2)延长AF,BC相交于点 P,当 时,求证:
25.(8分)如图,在正方形ABCD 中, E 是对角线AC上一动点,连接DE,作 EF⊥DE 交边 BC 或边 BC 的延长线于点F,以 DE 和EF 为邻边构造矩形DEFG,连接CG.
(1)若点 E 到边 BC 的距离为3,则它到边 DC 的距离为_________;
(2)求证:矩形 DEFG 是正方形;
(3)线段 AE 和线段CG.的数量关系是_________,位置关系是_________.
参考答案
1. A 2. B 3. D 4. B 5. C 6. A 7. D 8. C 9. A
10. D 解析:如图,连接AF,
∵四边形ABCD 是正方形,∴AB=BE=BC,∠ABC=90°,
∴∠BEC=∠BCE,∴∠EBC=180°-2∠BEC,∴∠ABE=∠ABC-∠EBC=2∠BEC-90°,
∵BF平分∠ABE, 45°,
∴∠BFE=∠BEC-∠EBF=45°,
在△BAF与△BEF中, ∴△BAF≌△BEF(SAS),
∴∠BFE=∠BFA=45°,∴∠AFC=∠BFA+∠BFE=90°,
∵O为对角线AC 的中点,
11. C
12. B 解析:∵四边形 ABCD是正方形, ∴AD=AB,∠DAB=∠ABC=90°,
又∵AE=BF,∴△ADE≌△BAF(SAS),∴∠ADE=∠BAF,
∴∠DOF =∠ADO+∠DAO=∠BAF+∠DAO=∠DAB=90°,
∵点 M 是 DF 的中点,
如图所示,在 AB 延长线上截取BH=BG,连接FH,
∵∠FBG=∠FBH=90°,FB=FB,BG=BH,∴△FBG≌△FBH(SAS),
∴FH=FG,
∴当H,D,F三点共线时,DF+HF有最小值,即此时 有最小值,最小值即为DH的长的一半,
∵AG=2GB,AB=6,∴BH=BG=2,∴AH=8,
在 Rt△ADH 中,由勾股定理得 DH = 的最小值为5.
13.四边相等的四边形是菱形 16. 5 17. 5
18. 3或-8或2或 (任写3个即可)
解析:如图1所示,
∵四边形ABDC 是菱形,∴点 B 与点 C 关于 AD 对称,AD 在 y轴上,
∴点C的坐标为(3,0),∴m的值等于3;
如图2所示,
∵四边形 ABCD 是菱形,
∴C点坐标为( ∴m的值等于
如图3所示,
∵四边形 ABCD 是菱形,
∴C点坐标为(2,0),∴m的值等于2;
如图4所示,
四边形 ADBC是菱形,
即 解得
综上所述,m的值等于3或 或2或
19.解:(1)证明:∵四边形 ABCD是平行四边形, ∥
∵AE,CF 分别是 的平分线,
∥
∥∴四边形 AECF 是平行四边形.
∵AE=AF,∴四边形AECF 是菱形;
(2)连接AC,
∵四边形 ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠AEB,
∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=EB,
∵∠ABC=60°,∴△ABE 是等边三角形,∴∠BAE=∠AEB=∠ABE=60°,
∵△ABE的面积等于 ∴AB=4,即AB=AE=EB=4,
由(1),得四边形 AECF 是菱形,∴AE=CE=4,∴∠EAC=∠ECA,
∵∠AEB 是△AEC的一个外角,∴∠AEB=∠EAC+∠ECA=60°,∴∠EAC=∠ECA=30°,
∴∠BAC=∠BAE+∠EAC=90°,即AC⊥AB,
由勾股定理得
即平行线 AB 与DC间的距离是
20.解:(1)证明:∵四边形 ABCD 是菱形,∴AD∥BC,即AD∥CE,
∵AC∥DE,∴四边形 ACED 是平行四边形;
(2)∵由(1),得四边形 ACED 是平行四边形,∴AC=DE=6,AC∥DE,
∵四边形ABCD为菱形,∴AB=AD=BC=5,AC⊥BD,∴BE=BC+CE=BC+AD=5+5=10,
∵AC∥DE,∴BD⊥DE,∴∠BDE=90°,
在 Rt△BDE 中,由勾股定理,得 BD = ∴BD的长为8.
21.解:(1)证明:∵四边形 ABCD为矩形,∴AD∥BC,∠B=90°,∴∠FAD=∠BEA.
∵DF⊥AE,∴∠DFA=90°=∠B.
在△ABE 和△DFA中, ∴△ABE≌△DFA(AAS),∴AB=DF;
(2)∵四边形ABCD 是矩形,∴BC=AD,∠B=90°,
设BC=x,则AD=BC=AE=x,BE=x-4,
解得x=10,∴BC=10.
22.解:(1)证明:∵∠GAF=∠F,∴∠AGC=∠F+∠GAF=2∠F,
∵∠ACG=∠AGC,∴∠ACG=2∠F,
∵四边形 ABCD是矩形,∴AD∥BC,∴∠ECB=∠F,
∴∠ACB=∠ACG+∠BCE=3∠F,即∠ACB=3∠ECB;
(2)∵∠F=15°,∴∠ACB=3×15°=45°=∠CAB,∴AB=BC,
又∵四边形ABCD 是矩形,∴四边形ABCD 是正方形,
∵正方形 ABCD面积为4,
∴△ABC的周长
23.证明:(1)∵四边形ADEF 是菱形,∴AD=AF,
∵∠BAC=∠DAF,∴∠BAD=∠CAF,
∵AB=AC,∴△BAD≌△CAF(SAS),∴BD=CF;
(2)∵四边形ADEF 是菱形,∴AD=AF,
∵∠BAC=∠DAF,∴∠BAD=∠CAF,
∵AB=AC,∴△BAD≌△CAF(SAS),∴BD=CF.
24.证明:(1)∵四边形ABCD 是菱形,∴AB=AD,AB∥CD,AD∥BC,∴∠ABD=∠ADB,
∵AE⊥BC,AF⊥CD,∴AE⊥AD,AF⊥AB,∴∠DAG=∠BAH=90°,
∴∠AHB=90°-∠ABD=90°-∠ADB=∠AGD,∴AH=AG;
(2)∵BG=GH,∴G是直角三角形ABH 斜边 BH 的中点,∴AG=BG=GH,
由(1),得AH=AG,∴AG=AH=GH,∴△AGH 是等边三角形,∴∠AHG=60°,
∴∠ABH=30°,∴∠ABC=60°,
∵AF⊥AB,∴∠BAP=90°,∴∠P=30°,
又∵AB∥CD,∴∠CFP=90°,∴CP=2CF,
如图,连接AC,
∵∠ADC=∠ABC=60°,AD=CD,∴△ADC是等边三角形,
∵AF⊥CD,∴CF=DF,
25.解:(1)如图,作EQ⊥BC于点Q,则EQ=3, EP⊥CD于点 P,
∵四边形ABCD是正方形,∴∠ACB=∠ACD=45°.
∵EP⊥CD,EQ⊥BC,∴EP=EQ=3.∴点 E 到边 DC 的距离为3,
故答案为:3;
(2)证明:∵∠EQC=∠EPC=∠BCD=90°,∴四边形 EQCP 是矩形.∴∠QEP=90°.
∵四边形 DEFG 是矩形,∴∠DEF=90°.∴∠DEP=∠FEQ.
∵∠EPD=∠EQF=90°,EP=EQ,∴△EPD≌△EQF(ASA).∴DE=FE,∴矩形 DEFG是正方形;
(3)∵四边形 DEFG是正方形,∴∠EDG=90°,DE=DG,
∵四边形ABCD是正方形,∴∠DAE=∠ACD=45°,∠ADC=90°,AD=CD,
∴∠ADC=∠EDG=90°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,∴∠ACD+∠DCG=90°,∴AE⊥CG,
综上可知,线段 AE 和线段CG 的数量关系是AE=CG,位置关系是AE⊥CG,
故答案为:AE=CG,AE⊥CG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
