第六章 特殊平行四边形 1 菱形的性质与判定 第1课时 菱形的性质(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 1 菱形的性质与判定 第1课时 菱形的性质(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-04 20:05:15 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
1 菱形的性质与判定
第1课时 菱形的性质
轻松过关
1.下列性质中,菱形不一定具备的是 ( )
A.四条边都相等 B.每一条对角线平分一组对角
C.邻角互补 D.对角线相等
2.如图,在菱形AOBC中, 点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )
第2题图 第3题图
3.如图所示,在菱形ABCD中,AB 的垂直平分线EF 交对角线 AC 于点 F,连接 DF,则等于 ( )
4.如图,菱形 ABCD 的边长为4,则菱形 ABCD 的面积为 ( )
A. 6 D. 12
第4题图 第5 题图
5.如图,菱形 ABCD的对角线AC 与BD 相交于点O,OE⊥BC于点E.若 则 ____________.
6.如图,菱形 ABCD的对角线的长分别为 4 和8,P是对角线AC上任一点(点P 不与点A,C重合),且 ∥BC交AB 于点E,PF∥CD交AD 于点F,则阴影部分的面积是__________.
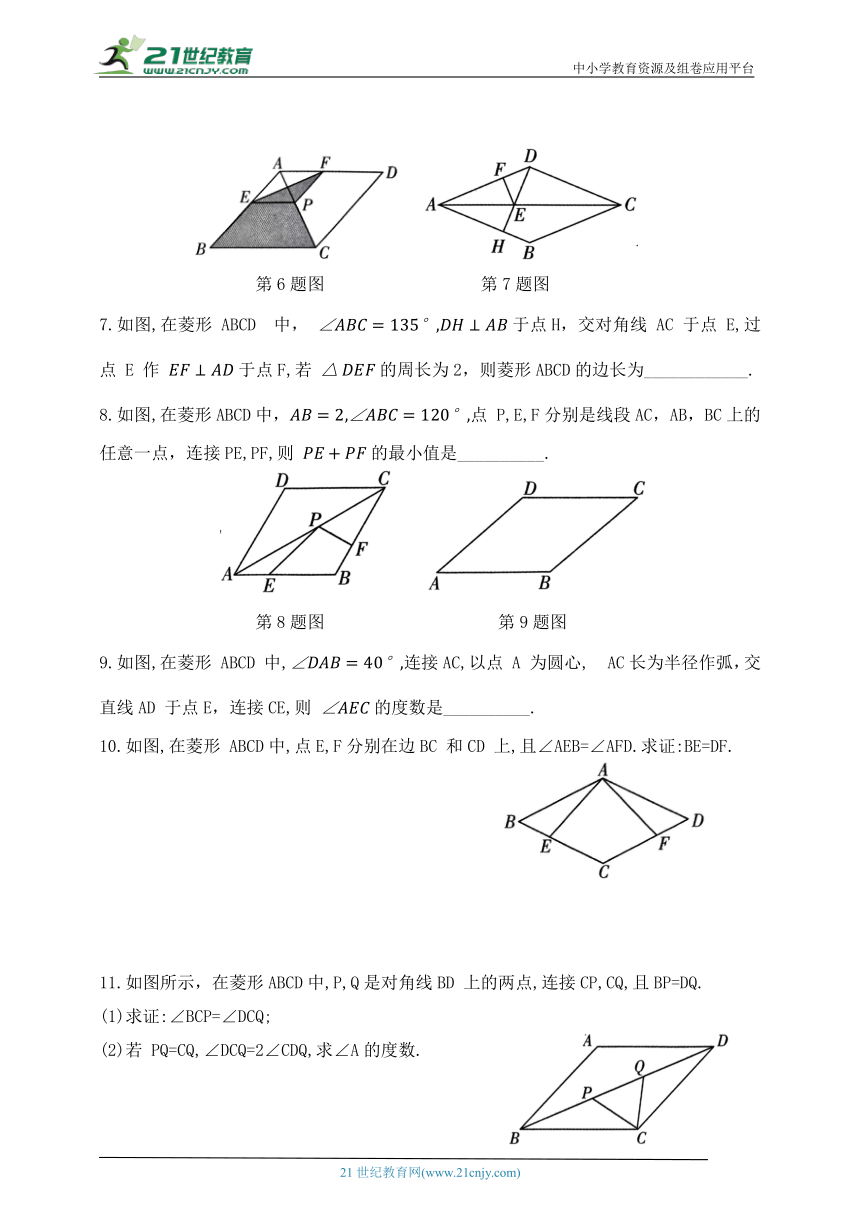
第6题图 第7题图
7.如图,在菱形 ABCD 中, 于点H,交对角线 AC 于点 E,过点 E 作 于点F,若 的周长为2,则菱形ABCD的边长为____________.
8.如图,在菱形ABCD中,点 P,E,F分别是线段AC,AB,BC上的任意一点,连接PE,PF,则 的最小值是__________.
第8题图 第9题图
9.如图,在菱形 ABCD 中,连接AC,以点 A 为圆心, AC长为半径作弧,交直线AD 于点E,连接CE,则 的度数是__________.
10.如图,在菱形 ABCD中,点E,F分别在边BC 和CD 上,且∠AEB=∠AFD.求证:BE=DF.
11.如图所示,在菱形ABCD中,P,Q是对角线BD 上的两点,连接CP,CQ,且BP=DQ.
(1)求证:∠BCP=∠DCQ;
(2)若 PQ=CQ,∠DCQ=2∠CDQ,求∠A的度数.
12.如图,四边形 ABCD 是菱形,AE⊥BC于点E,AF⊥CD 于点F.
(1)求证:△ABE≌△ADF;
(2)若AE=4,CF=2,求菱形的边长.
13.如图所示,在菱形ABCD中,60°<∠ABC<90°,点 E 在边BC 上(不与点 B,点 C 重合),线段 EC 的中垂线交对角线 BD 于点 F,连接 AE,AF,EF,CF.
(1)求证:AF=EF;
(2)若∠ABC=2∠AEF,AB=AE,AB∥FE,求证:BF=CF+CE.
快乐拓展
14.如图,四边形 ABCD 为菱形,AB=2,∠ABC =60°,E,F为BD 上的两个动点,且 BE+DF=EF,点 M 是AD 的中点,连接CE,MF,则CE+MF 的最小值为____________.
15.如图,菱形 ABCD 的边长为2,BD=2,E,F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)试探究△DEF 的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△DEF 周长的最小值.
参考答案
1. D 2. A 3. D 4. C
7. 2 8. 9.10°或80°
10.证明:∵四边形 ABCD是菱形,∴AB=AD,∠B=∠D.
在△ABE和△ADF 中, ∴△ABE≌△ADF(AAS),∴BE=DF.
11.解:(1)证明:∵四边形 ABCD 是菱形,∴BC=CD,∠CBD=∠CDB,
在△BCP 和△DCQ中, ∴△BCP≌△DCQ(SAS),
∴∠BCP=∠DCQ;
(2)∵△BCP≌△DCQ,∴CP=CQ,
∵PQ=CQ,∴△PCQ是等边三角形,∴∠PQC=60°,
∵∠DCQ=2∠CDQ,∠PQC=∠DCQ+∠CDQ,∴∠DCQ=∠BCP=40°,∴∠BCD=140°,
∵四边形ABCD 是菱形,∴∠A=∠BCD=140°.
12.解:(1)证明:∵四边形 ABCD 是菱形,∴AB=BC=CD=AD,∠B=∠D,
∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD,
在△ABE和△ADF中, ∴△ABE≌△ADF(AAS);
(2)设菱形的边长为x,即AB=CD=x,又∵CF=2,∴DF=x-2,
∵△ABE≌△ADF,∴BE=DF=x-2,
在 Rt△ABE中,由勾股定理,得
即 解得x=5,∴菱形的边长是5.
13.证明:(1)∵四边形 ABCD 是菱形,∴∠ABD=∠CBD,AB=CB,
∵BF=BF,∴△ABF≌△CBF(SAS),∴AF=CF,
又∵线段 EC的中垂线交BD 于点 F,∴EF=CF,∴AF=FE;
(2)∵AB=AE,∴∠ABE=∠AEB,
∵AB∥FE,∴∠FEC=∠ABE,∴∠FEC=∠ABE=∠AEB=∠ECF,
∵∠AEB+∠CEF+∠AEF=180°,∠ABC=2∠AEF,∴∠AEF = 36°=∠CBF, ∠FEC =∠BCF=72°,
∴∠BFC=72°,∠BFE=36°,
∵∠BFC=∠BCF=72°,∴BF=BC,
∵∠BFE=∠FBC=36°,∴BE=EF=CF,
∴BF=BC=BE+CE=CF+CE.
15.解:(1)证明:∵菱形 ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,∴△ABD与△BCD都是等边三角形,∴∠BDE=∠C=60°,
∵AE+CF=2,∴CF=2-AE,
又∵DE=AD-AE=2-AE,∴DE=CF,
在△BDE和△BCF中,∴△BDE≌△BCF(SAS);
(2)△BEF 是等边三角形.理由如下:
由(1),得△BDE≌△BCF,∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF 是等边三角形;
(3)存在.如图所示:
∵△BDE≌△BCF,∴DE=FC,∴DE+DF=AD=2,
故当△DEF的周长最小,则EF最小即可,
∵△BEF 是等边三角形,△ABD 与△BCD都是等边三角形,
∴当BE⊥AD时,EF最小,此时
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
1 菱形的性质与判定
第1课时 菱形的性质
轻松过关
1.下列性质中,菱形不一定具备的是 ( )
A.四条边都相等 B.每一条对角线平分一组对角
C.邻角互补 D.对角线相等
2.如图,在菱形AOBC中, 点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )
第2题图 第3题图
3.如图所示,在菱形ABCD中,AB 的垂直平分线EF 交对角线 AC 于点 F,连接 DF,则等于 ( )
4.如图,菱形 ABCD 的边长为4,则菱形 ABCD 的面积为 ( )
A. 6 D. 12
第4题图 第5 题图
5.如图,菱形 ABCD的对角线AC 与BD 相交于点O,OE⊥BC于点E.若 则 ____________.
6.如图,菱形 ABCD的对角线的长分别为 4 和8,P是对角线AC上任一点(点P 不与点A,C重合),且 ∥BC交AB 于点E,PF∥CD交AD 于点F,则阴影部分的面积是__________.
第6题图 第7题图
7.如图,在菱形 ABCD 中, 于点H,交对角线 AC 于点 E,过点 E 作 于点F,若 的周长为2,则菱形ABCD的边长为____________.
8.如图,在菱形ABCD中,点 P,E,F分别是线段AC,AB,BC上的任意一点,连接PE,PF,则 的最小值是__________.
第8题图 第9题图
9.如图,在菱形 ABCD 中,连接AC,以点 A 为圆心, AC长为半径作弧,交直线AD 于点E,连接CE,则 的度数是__________.
10.如图,在菱形 ABCD中,点E,F分别在边BC 和CD 上,且∠AEB=∠AFD.求证:BE=DF.
11.如图所示,在菱形ABCD中,P,Q是对角线BD 上的两点,连接CP,CQ,且BP=DQ.
(1)求证:∠BCP=∠DCQ;
(2)若 PQ=CQ,∠DCQ=2∠CDQ,求∠A的度数.
12.如图,四边形 ABCD 是菱形,AE⊥BC于点E,AF⊥CD 于点F.
(1)求证:△ABE≌△ADF;
(2)若AE=4,CF=2,求菱形的边长.
13.如图所示,在菱形ABCD中,60°<∠ABC<90°,点 E 在边BC 上(不与点 B,点 C 重合),线段 EC 的中垂线交对角线 BD 于点 F,连接 AE,AF,EF,CF.
(1)求证:AF=EF;
(2)若∠ABC=2∠AEF,AB=AE,AB∥FE,求证:BF=CF+CE.
快乐拓展
14.如图,四边形 ABCD 为菱形,AB=2,∠ABC =60°,E,F为BD 上的两个动点,且 BE+DF=EF,点 M 是AD 的中点,连接CE,MF,则CE+MF 的最小值为____________.
15.如图,菱形 ABCD 的边长为2,BD=2,E,F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)试探究△DEF 的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△DEF 周长的最小值.
参考答案
1. D 2. A 3. D 4. C
7. 2 8. 9.10°或80°
10.证明:∵四边形 ABCD是菱形,∴AB=AD,∠B=∠D.
在△ABE和△ADF 中, ∴△ABE≌△ADF(AAS),∴BE=DF.
11.解:(1)证明:∵四边形 ABCD 是菱形,∴BC=CD,∠CBD=∠CDB,
在△BCP 和△DCQ中, ∴△BCP≌△DCQ(SAS),
∴∠BCP=∠DCQ;
(2)∵△BCP≌△DCQ,∴CP=CQ,
∵PQ=CQ,∴△PCQ是等边三角形,∴∠PQC=60°,
∵∠DCQ=2∠CDQ,∠PQC=∠DCQ+∠CDQ,∴∠DCQ=∠BCP=40°,∴∠BCD=140°,
∵四边形ABCD 是菱形,∴∠A=∠BCD=140°.
12.解:(1)证明:∵四边形 ABCD 是菱形,∴AB=BC=CD=AD,∠B=∠D,
∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD,
在△ABE和△ADF中, ∴△ABE≌△ADF(AAS);
(2)设菱形的边长为x,即AB=CD=x,又∵CF=2,∴DF=x-2,
∵△ABE≌△ADF,∴BE=DF=x-2,
在 Rt△ABE中,由勾股定理,得
即 解得x=5,∴菱形的边长是5.
13.证明:(1)∵四边形 ABCD 是菱形,∴∠ABD=∠CBD,AB=CB,
∵BF=BF,∴△ABF≌△CBF(SAS),∴AF=CF,
又∵线段 EC的中垂线交BD 于点 F,∴EF=CF,∴AF=FE;
(2)∵AB=AE,∴∠ABE=∠AEB,
∵AB∥FE,∴∠FEC=∠ABE,∴∠FEC=∠ABE=∠AEB=∠ECF,
∵∠AEB+∠CEF+∠AEF=180°,∠ABC=2∠AEF,∴∠AEF = 36°=∠CBF, ∠FEC =∠BCF=72°,
∴∠BFC=72°,∠BFE=36°,
∵∠BFC=∠BCF=72°,∴BF=BC,
∵∠BFE=∠FBC=36°,∴BE=EF=CF,
∴BF=BC=BE+CE=CF+CE.
15.解:(1)证明:∵菱形 ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,∴△ABD与△BCD都是等边三角形,∴∠BDE=∠C=60°,
∵AE+CF=2,∴CF=2-AE,
又∵DE=AD-AE=2-AE,∴DE=CF,
在△BDE和△BCF中,∴△BDE≌△BCF(SAS);
(2)△BEF 是等边三角形.理由如下:
由(1),得△BDE≌△BCF,∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF 是等边三角形;
(3)存在.如图所示:
∵△BDE≌△BCF,∴DE=FC,∴DE+DF=AD=2,
故当△DEF的周长最小,则EF最小即可,
∵△BEF 是等边三角形,△ABD 与△BCD都是等边三角形,
∴当BE⊥AD时,EF最小,此时
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
