第六章 特殊平行四边形 1 菱形的性质与判定 第2课时 菱形的判定(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 1 菱形的性质与判定 第2课时 菱形的判定(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-04 20:09:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
1 菱形的性质与判定
第2课时 菱形的判定
轻松过关
1.下列选项中能使 ABCD成为菱形的是 ( )
A. AB=CD B. AB=BC C.∠BAD=90° D. AC=BD
2.如图,在 ABCD中, E,F分别是AB,CD的中点,连接EF.如果只添加一个条件即可证明四边形AEFD是菱形,那么这个条件可以是 ( )
第2题图 第3题图
A. AB⊥AD B.∠BAD=60° C. AD=EF D. CD=2AD
3.如图,在△ABC中, AD是角平分线,DE∥AC 交AB 于点 E, DF∥AB交AC 于点F,若AE=3,那么四边形 AEDF 周长为 ( )
A. 9 B. 12 C. 15 D. 18
4.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得 A,C 两点之间的距离为12 cm,B,D两点之间的距离为16 cm,则这两张纸条的宽为 ( )
A. 19.2 cm B. 10 cm C. 9.6 cm D. 4.8 cm
第4题图 第5题图
5.如图,在菱形ABCD 中,∠BAD=60°,AC与BD 交于点O,E为CD 延长线上的一点,且DE=CD,连接BE 分别交AC,AD于点F,G,连接OG.则下列结论:① ②∠FOG=30° ③S四边形ODEG=S四边形ABOG ④由点 A,B,D,E构成的四边形是菱形.其中正确的个数是 ( )
A. 4 B. 3 C. 2 D. 1
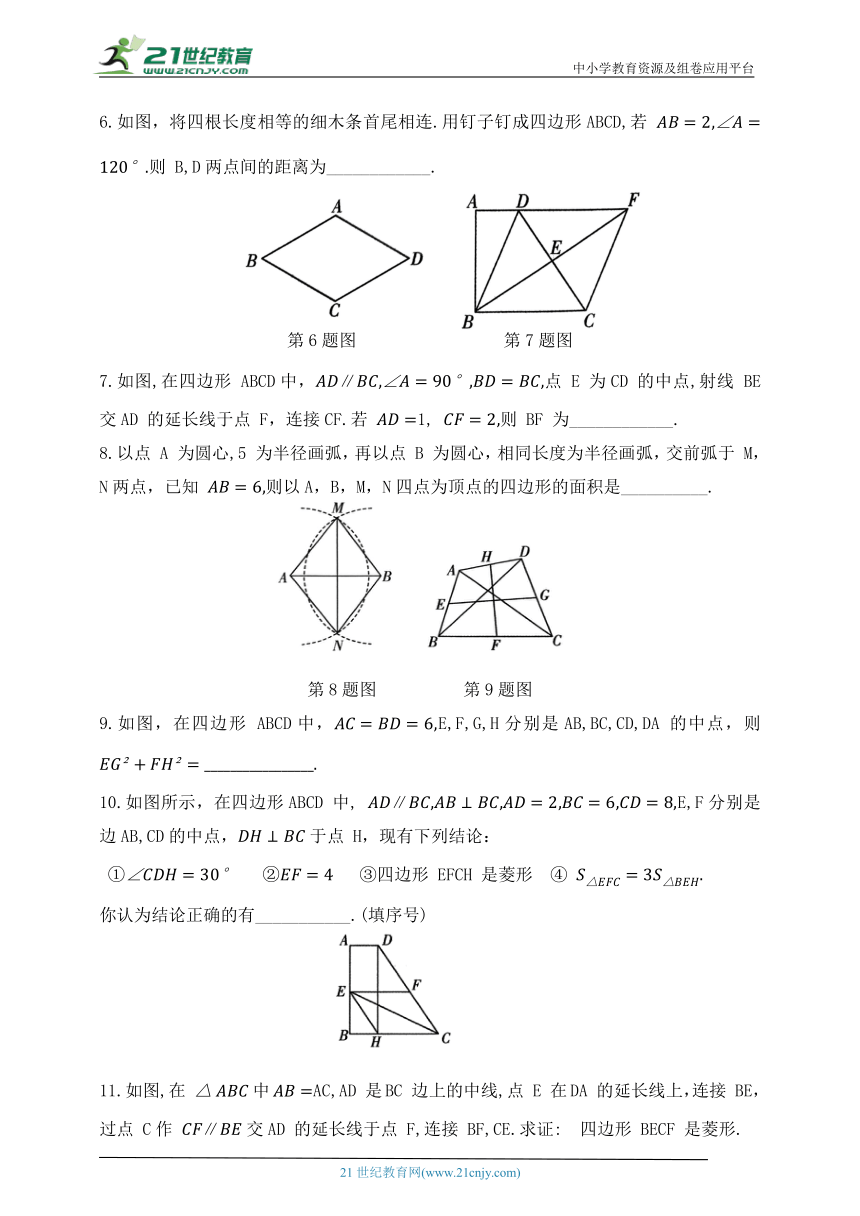
6.如图,将四根长度相等的细木条首尾相连.用钉子钉成四边形ABCD,若 则 B,D两点间的距离为____________.
第6题图 第7题图
7.如图,在四边形 ABCD中,∥点 E 为CD 的中点,射线 BE交AD 的延长线于点 F,连接CF.若 1, 则 BF 为____________.
8.以点 A 为圆心,5 为半径画弧,再以点 B 为圆心,相同长度为半径画弧,交前弧于 M,N两点,已知 则以A,B,M,N四点为顶点的四边形的面积是__________.
第8题图 第9题图
9.如图,在四边形 ABCD中,E,F,G,H分别是AB,BC,CD,DA 的中点,则
10.如图所示,在四边形ABCD 中, ∥E,F分别是边AB,CD的中点,于点 H,现有下列结论:
③四边形 EFCH 是菱形 ④
你认为结论正确的有___________.(填序号)
11.如图,在 中AC,AD 是BC 边上的中线,点 E 在DA 的延长线上,连接 BE,过点 C作 ∥交AD 的延长线于点 F,连接 BF,CE.求证: 四边形 BECF 是菱形.
12.如图,在 中,AC,BD交于点O,点E,F在AC上,
(1)求证:四边形 EBFD是平行四边形;
(2)若 求证:四边形EBFD是菱形.
13.如图,在 中,D是AB 上一点, 于点 E,F 是AD 的中点, 于点G,与 DE 交于点H,若 AG平分 连接GE,GD.
(1)求证:
(2)当 为多少度时,四边形AEGF 为菱形,请说明理由.
快乐拓展
14.如图,在 中,点 D 从点 C 出发沿CA 方向以每秒2个单位长度的速度向点 A 匀速运动,同时点 E 从点 A 出发沿AB 方向以每秒1个单位长度的速度向点 B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点 D,E运动的时间是t秒 过点 D 作 于点F,连接 DE,EF.
(用含t的式子表示);
(2)四边形 AEFD 能成为菱形吗 如果能,求出相应的 t 的值;如果不能,说明理由;
(3)当 ___________秒时, 为直角三角形.
15.如图,在边长为10的菱形 ABCD中,对角线 对角线AC,BD 相交于点G,点 O 是直线BD上的动点, 于点E, 于点F.
(1)求对角线 AC 的长及菱形 ABCD的面积;
(2)如图1,当点 O 在对角线 BD 上运动时, 的值是否发生变化 请说明理由;
(3)如图2,当点O在对角线 BD 的延长线上时, 的值是否发生变化 若不变,请说明理由;若变化,请探究 OE,OF之间的数量关系.
参考答案
1. B 2. D 3. B 4. C 5. A
8. 24 9. 36 10. ①②③
11.证明: AD是BC 边上的中线,∴AD垂直平分BC,
∥
∵DB=CD,∴△EBD≌△FCD(AAS),∴BE=FC,
∴EB=BF=FC=EC,∴四边形 BECF 是菱形.
12.证明:(1)∵四边形ABCD为平行四边形,∴OA=OC,OB=OD,
∵AE=CF,∴OE=OF,∴四边形 EBFD是平行四边形;
(2)∵四边形 ABCD是平行四边形,∴AB∥DC,∴∠BAC=∠DCA,
∵∠BAC=∠DAC,∴∠DCA=∠DAC,∴DA=DC,
∴平行四边形ABCD为菱形,∴DB⊥EF,∴平行四边形 EBFD 是菱形.
13.解:(1)证明:∵AF=FG,∴∠FAG=∠FGA,
∵AG平分∠CAB,∴∠CAG=∠FAG,∴∠CAG=∠FGA,∴AC∥FG,
∵DE⊥AC,∴FG⊥DE,
∵FG⊥BC,∴DE∥BC,∴AC⊥BC,∠CGE=∠GED,∴∠C=90°,
∵F是AD的中点,FG∥AE,∴FH 是△ADE的中位线,∴H是ED的中点
∴FG 是线段ED的垂直平分线,∴GE=GD,∠DHG=90°,
∴∠GDE=∠GED,∴∠CGE=∠GDE,
在△ECG 和△GHD中, ∴△ECG≌△GHD(AAS);
(2)当∠B为30°时,四边形 AEGF 为菱形,理由如下:
由(1),得 DE∥BC,∴∠ADE=∠B=30°, ∴AE=AF=FG,
由(1),得AE∥FG,∴四边形 AEGF 是平行四边形,
∵AE=AF,∴四边形AEGF 是菱形.
14.解:(1)由题意,得CD=2t,AE=t.
∵DF⊥BC,∠C=30°, ∴AE=t,DF=t.
故答案为:t;t;
(2)四边形AEFD 能成为菱形, 理由:
由(1),得AE=DF.
∵∠B=90°,∴AB⊥BC,
∵DF⊥BC,∴AE∥DF,∴四边形 AEFD为平行四边形,
∴四边形 AEFD 如果能够成为菱形,则需AE=AD.
∵∠B=90°,∠C=30°,AB=5,∴AC=2AB=10,∴AD=AC-CD=10-2t,
∴t=10-2t,解得
∴四边形AEFD能够成为菱形,
(3)①∵DF⊥BC,∴∠DFB=90°,
∵∠DFE<∠DFB,∴∠DFE<90°.∴∠DFE不可能为直角;
②当∠EDF=90°时,
∵DE⊥DF,DF⊥BC,∴DE∥BC,
∵AB∥DF,∴四边形 EBFD为平行四边形,∴DF=BE,∴t=5-t,
③当∠DEF=90°时,如图,
由(1)得四边形AEFD为平行四边形,∥
解得
综上所述,当 或4 时, 为直角三角形.故答案为: 或4.
15.解:(1)∵四边形 ABCD为菱形,
由勾股定理,得 ∴AC=2AG=2×6=12,
96;
的值不变,理由:
如图 1,连接 AO,则 OF,
即 解得 是定值,不变;
的值改变,
如图 2,连 接 AO,则
即 解得( 是定值,不变,
的值变化,OE,OF 之间的数量关系为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
1 菱形的性质与判定
第2课时 菱形的判定
轻松过关
1.下列选项中能使 ABCD成为菱形的是 ( )
A. AB=CD B. AB=BC C.∠BAD=90° D. AC=BD
2.如图,在 ABCD中, E,F分别是AB,CD的中点,连接EF.如果只添加一个条件即可证明四边形AEFD是菱形,那么这个条件可以是 ( )
第2题图 第3题图
A. AB⊥AD B.∠BAD=60° C. AD=EF D. CD=2AD
3.如图,在△ABC中, AD是角平分线,DE∥AC 交AB 于点 E, DF∥AB交AC 于点F,若AE=3,那么四边形 AEDF 周长为 ( )
A. 9 B. 12 C. 15 D. 18
4.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得 A,C 两点之间的距离为12 cm,B,D两点之间的距离为16 cm,则这两张纸条的宽为 ( )
A. 19.2 cm B. 10 cm C. 9.6 cm D. 4.8 cm
第4题图 第5题图
5.如图,在菱形ABCD 中,∠BAD=60°,AC与BD 交于点O,E为CD 延长线上的一点,且DE=CD,连接BE 分别交AC,AD于点F,G,连接OG.则下列结论:① ②∠FOG=30° ③S四边形ODEG=S四边形ABOG ④由点 A,B,D,E构成的四边形是菱形.其中正确的个数是 ( )
A. 4 B. 3 C. 2 D. 1
6.如图,将四根长度相等的细木条首尾相连.用钉子钉成四边形ABCD,若 则 B,D两点间的距离为____________.
第6题图 第7题图
7.如图,在四边形 ABCD中,∥点 E 为CD 的中点,射线 BE交AD 的延长线于点 F,连接CF.若 1, 则 BF 为____________.
8.以点 A 为圆心,5 为半径画弧,再以点 B 为圆心,相同长度为半径画弧,交前弧于 M,N两点,已知 则以A,B,M,N四点为顶点的四边形的面积是__________.
第8题图 第9题图
9.如图,在四边形 ABCD中,E,F,G,H分别是AB,BC,CD,DA 的中点,则
10.如图所示,在四边形ABCD 中, ∥E,F分别是边AB,CD的中点,于点 H,现有下列结论:
③四边形 EFCH 是菱形 ④
你认为结论正确的有___________.(填序号)
11.如图,在 中AC,AD 是BC 边上的中线,点 E 在DA 的延长线上,连接 BE,过点 C作 ∥交AD 的延长线于点 F,连接 BF,CE.求证: 四边形 BECF 是菱形.
12.如图,在 中,AC,BD交于点O,点E,F在AC上,
(1)求证:四边形 EBFD是平行四边形;
(2)若 求证:四边形EBFD是菱形.
13.如图,在 中,D是AB 上一点, 于点 E,F 是AD 的中点, 于点G,与 DE 交于点H,若 AG平分 连接GE,GD.
(1)求证:
(2)当 为多少度时,四边形AEGF 为菱形,请说明理由.
快乐拓展
14.如图,在 中,点 D 从点 C 出发沿CA 方向以每秒2个单位长度的速度向点 A 匀速运动,同时点 E 从点 A 出发沿AB 方向以每秒1个单位长度的速度向点 B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点 D,E运动的时间是t秒 过点 D 作 于点F,连接 DE,EF.
(用含t的式子表示);
(2)四边形 AEFD 能成为菱形吗 如果能,求出相应的 t 的值;如果不能,说明理由;
(3)当 ___________秒时, 为直角三角形.
15.如图,在边长为10的菱形 ABCD中,对角线 对角线AC,BD 相交于点G,点 O 是直线BD上的动点, 于点E, 于点F.
(1)求对角线 AC 的长及菱形 ABCD的面积;
(2)如图1,当点 O 在对角线 BD 上运动时, 的值是否发生变化 请说明理由;
(3)如图2,当点O在对角线 BD 的延长线上时, 的值是否发生变化 若不变,请说明理由;若变化,请探究 OE,OF之间的数量关系.
参考答案
1. B 2. D 3. B 4. C 5. A
8. 24 9. 36 10. ①②③
11.证明: AD是BC 边上的中线,∴AD垂直平分BC,
∥
∵DB=CD,∴△EBD≌△FCD(AAS),∴BE=FC,
∴EB=BF=FC=EC,∴四边形 BECF 是菱形.
12.证明:(1)∵四边形ABCD为平行四边形,∴OA=OC,OB=OD,
∵AE=CF,∴OE=OF,∴四边形 EBFD是平行四边形;
(2)∵四边形 ABCD是平行四边形,∴AB∥DC,∴∠BAC=∠DCA,
∵∠BAC=∠DAC,∴∠DCA=∠DAC,∴DA=DC,
∴平行四边形ABCD为菱形,∴DB⊥EF,∴平行四边形 EBFD 是菱形.
13.解:(1)证明:∵AF=FG,∴∠FAG=∠FGA,
∵AG平分∠CAB,∴∠CAG=∠FAG,∴∠CAG=∠FGA,∴AC∥FG,
∵DE⊥AC,∴FG⊥DE,
∵FG⊥BC,∴DE∥BC,∴AC⊥BC,∠CGE=∠GED,∴∠C=90°,
∵F是AD的中点,FG∥AE,∴FH 是△ADE的中位线,∴H是ED的中点
∴FG 是线段ED的垂直平分线,∴GE=GD,∠DHG=90°,
∴∠GDE=∠GED,∴∠CGE=∠GDE,
在△ECG 和△GHD中, ∴△ECG≌△GHD(AAS);
(2)当∠B为30°时,四边形 AEGF 为菱形,理由如下:
由(1),得 DE∥BC,∴∠ADE=∠B=30°, ∴AE=AF=FG,
由(1),得AE∥FG,∴四边形 AEGF 是平行四边形,
∵AE=AF,∴四边形AEGF 是菱形.
14.解:(1)由题意,得CD=2t,AE=t.
∵DF⊥BC,∠C=30°, ∴AE=t,DF=t.
故答案为:t;t;
(2)四边形AEFD 能成为菱形, 理由:
由(1),得AE=DF.
∵∠B=90°,∴AB⊥BC,
∵DF⊥BC,∴AE∥DF,∴四边形 AEFD为平行四边形,
∴四边形 AEFD 如果能够成为菱形,则需AE=AD.
∵∠B=90°,∠C=30°,AB=5,∴AC=2AB=10,∴AD=AC-CD=10-2t,
∴t=10-2t,解得
∴四边形AEFD能够成为菱形,
(3)①∵DF⊥BC,∴∠DFB=90°,
∵∠DFE<∠DFB,∴∠DFE<90°.∴∠DFE不可能为直角;
②当∠EDF=90°时,
∵DE⊥DF,DF⊥BC,∴DE∥BC,
∵AB∥DF,∴四边形 EBFD为平行四边形,∴DF=BE,∴t=5-t,
③当∠DEF=90°时,如图,
由(1)得四边形AEFD为平行四边形,∥
解得
综上所述,当 或4 时, 为直角三角形.故答案为: 或4.
15.解:(1)∵四边形 ABCD为菱形,
由勾股定理,得 ∴AC=2AG=2×6=12,
96;
的值不变,理由:
如图 1,连接 AO,则 OF,
即 解得 是定值,不变;
的值改变,
如图 2,连 接 AO,则
即 解得( 是定值,不变,
的值变化,OE,OF 之间的数量关系为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
