第六章 特殊平行四边形 3 正方形的性质与判定 第2课时 正方形的判定(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 3 正方形的性质与判定 第2课时 正方形的判定(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-04 20:10:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
3 正方形的性质与判定
第2课时 正方形的判定
轻松过关
1.学习了正方形之后,老师提出问题:要判断一个四边形是正方形,有哪些思路
甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:先判定四边形的对角线相等,再确定对角线互相垂直;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是 ( )
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丁
2.一个四边形顺次添加下列条件中的三个条件便得到正方形:a.两组对边分别相等;b.一组对边平行且相等;c.一组邻边相等;d.一个角是直角.顺次添加的条件:①a→c→d ②b→d→c ③a→b→c.其中正确的是 ( )
A. ①② B. 仅③ C. 仅① D. ②③
3.如图, 在 △ABC 中,∠ACB=90°, BC 的垂直平分线 EF 交 BC 于点D,交 AB 于点 E,且BE= BF,添加一个条件,仍不能证明四边形BECF 为正方形的是 ( )
A. BC=AC B. BD=DF C. AC=BF D. CF⊥BF
第3题图 第4题图
4.如图,AC,BD 是四边形ABCD 的对角线,点E,F分别是AD,BC 的中点,点 M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是 ( )
∥
5.在矩形 ABCD中,M,N,P,Q分别为边 AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下列结论:①存在无数个四边形 MNPQ是平行四边形 ②存在无数个四边形 MNPQ是矩形 ③存在无数个四边形 MNPQ是菱形 ④至少存在一个四边形 MNPQ是正方形.
其中正确结论的序号是 ( )
A. ①③ B. ②③ C. ①②③ D. ①②③④
6.如图,在平行四边形ABCD中,对角线 AC与BD 相交于点E,点 G 为 AD 的中点,连接 CG,CG 的延长线交BA 的延长线于点 F,连接 DF.当 满足__________时,四边形 ACDF 为正方形.
第6题图 第7题图
7.如图,在矩形ABCD中,AC交 BD 于点O,且. 10 cm,将AC绕点C 顺时针旋转 至CE,连接AE,且 F,G分别为AE,EC的中点,则四边形 OFGC 的面积是________.
8.如图,□ABCD的对角线 AC,BD 相交于点 O,且 AE∥BD,BE∥AC,OE=CD.若AD=2,则当四边形ABCD 的形状是_时,四边形 AOBE的面积取得最大值是___________.
第8题图 第9题图
9.已知平行四边形ABCD,对角线AC与BD 相交于点O,点 P在边AD上,过点 P 分别作PE⊥AC,PF⊥BD,垂足分别为点 E,F,PE=PF.
(1)如图,若∠EPF=60°,EO=1,则 PE 的长_____________;
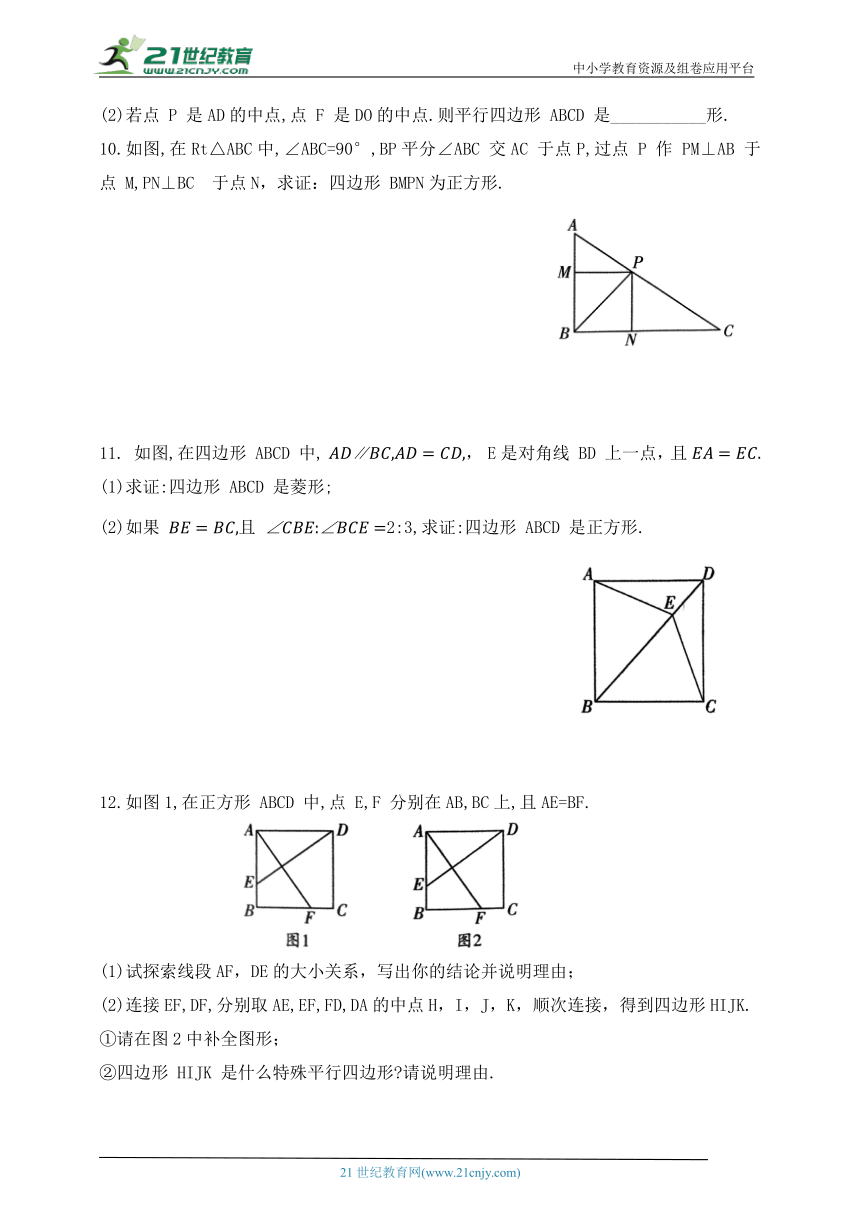
(2)若点 P 是AD的中点,点 F 是DO的中点.则平行四边形 ABCD 是___________形.
10.如图,在Rt△ABC中,∠ABC=90°,BP平分∠ABC 交AC 于点P,过点 P 作 PM⊥AB 于点 M,PN⊥BC 于点N,求证:四边形 BMPN为正方形.
11. 如图,在四边形 ABCD 中, ∥, E是对角线 BD 上一点,且
(1)求证:四边形 ABCD 是菱形;
(2)如果 且 2:3,求证:四边形 ABCD 是正方形.
12.如图1,在正方形 ABCD 中,点 E,F 分别在AB,BC上,且AE=BF.
(1)试探索线段AF,DE的大小关系,写出你的结论并说明理由;
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,顺次连接,得到四边形HIJK.
①请在图2中补全图形;
②四边形 HIJK 是什么特殊平行四边形 请说明理由.
13.如图,在等腰直角三角形ABC中, D是AB 的中点,E,F 分别是AC,BC 上的点(点E 不与端点 A,C重合),且连接 EF 并取EF 的中点O,连接DO并延长至点G,使 连接DE,DF,GE,GF.
(1)求证:四边形 EDFG是正方形;
(2)当点 E 在什么位置时,四边形 EDFG的面积最小 并求四边形 EDFG 面积的最小值.
快乐拓展
14.如图,以△ABC的三边为边在 BC上方分别作等边△ACD,△ABE,△BCF,且点 A 在△BCF 内部.给出下列结论:①四边形ADFE 是平行四边形 ②当AB=AC时,四边形 ADFE 是菱形③当∠BAC=90°时,四边形ADFE 是矩形 ④当AB=AC,且 时,四边形ADFE 是正方形.其中正确结论有__________(填序号).
15.四边形ABCD为正方形,点 E 为对角线AC上一点,连接 DE,BE.过点 E作交射线 BC 于点 F.
(1)如图 1,若点 F 在边 BC 上,求证:
(2)如图 2,以 DE,EF 为邻边作矩形DEFG,连接CG,若 求CG的长度;
(3)若矩形 DEFG 的边 DE 与正方形ABCD一边的夹角是时,直接写出的度数.
参考答案
1. D 2. A 3. C 4. A 5. C
6. AB=AC,∠BAC=90° 8.正方形 2 (2) 正方
10.证明:∵PM⊥AB,PN⊥BC,∴∠PMB=∠PNB=90°,
∵∠ABC=90°,∴四边形 BMPN 是矩形,
∵BP平分∠ABC,PM⊥AB,PN⊥BC,∴PM=PN,∴四边形 BMPN 为正方形.
11.证明:(1)在△ADE与△CDE中,
∴△ADE≌△CDE(SSS),∴∠ADE=∠CDE,
∵AD∥BC,∴∠ADE=∠CBD,∴∠CDE=∠CBD,∴BC=CD,
∵AD=CD,∴BC=AD,∴四边形 ABCD为平行四边形,
∵AD=CD,∴四边形 ABCD 是菱形;
(2)∵BE=BC,∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,
∵四边形 ABCD 是菱形,∴∠ABE=45°,∴∠ABC=90°,∴四边形 ABCD 是正方形.
12.解:(1)AF=DE,理由如下:
∵四边形 ABCD是正方形,∴AD=AB,∠DAE=∠ABF=90°,
∵AE=BF,∴△DAE≌△ABF(SAS),∴AF=DE;
(2)①如图:
②四边形 HIJK 是正方形.理由如下:
∵H,I分别是AE,EF的中点,∴HI是△AEF的中位线, ∥
同理 ∥∴HI=KJ,HI∥KJ,同理 HK=IJ,HK∥IJ,
∵AF=DE,∴HI=KJ=HK=IJ,∴四边形 HIJK 是菱形.
∵△DAE≌△ABF,∴∠ADE=∠BAF,
∵∠ADE+∠AED=90°,∴∠BAF+∠AED=90°,∴∠AOE=90°,
又∵ED∥HK,HI∥AF,∴HK⊥HI,∴∠KHI=90°,
∴四边形 HIJK 是正方形.
13.解:(1)证明:连接CD,如图1所示.
∵△ABC为等腰直角三角形,∠ACB=90°,D是AB 的中点,∴∠A=∠DCF=45°,AD=CD.
在△ADE和△CDF中,∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF.
∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,∴△EDF为等腰直角三角形.
∵OE=OF,OG=OD,∴四边形 EDFG为平行四边形,
∵DE=DF,∴平行四边形 EDFG 为菱形,
∵∠EDF=90°,∴四边形 EDFG 是正方形;
(2)过点 D 作. 于点 如图2所示.
∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC=4,
点 E'为AC的中点,
(点E 与点 重合时取等号).
∴当点 E 为线段 AC 的中点时,四边形EDFG的面积最小,该最小值为4.
14. ①②
15.解:(1)证明:
∵四边形 ABCD 是正方形,AC 为其对角线,∴BC=DC,∠BCE=∠DCE,
∵EC=EC,∴△BCE≌△DCE(SAS),∴∠EBF=∠EDC,BE=DE,
∵四边形 ABCD是正方形,∴∠DCF=90°,
∵DE⊥EF,∴∠DEF=90°,∴∠CDE+∠CFE = 360°-(∠DCF+∠DEF)=180°,
∵∠CFE+∠EFB=180°,∴∠EBF=∠EFB,∴BE=EF,∴DE=EF;
(2)∵四边形 DEFG为矩形,DE=EF,∴四边形 DEFG 为正方形,∴DE=DG,
∵四边形 ABCD 为正方形,∴AD=DC,∠ADC=90°=∠EDG,∴∠ADE=∠CDG,
∴△ADE≌△CDG(SAS),∴AE=CG,
∵AB=4,
(3)当∠ADE=35°时,如图2,
当 时,如图3,
综上所述, 或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
3 正方形的性质与判定
第2课时 正方形的判定
轻松过关
1.学习了正方形之后,老师提出问题:要判断一个四边形是正方形,有哪些思路
甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:先判定四边形的对角线相等,再确定对角线互相垂直;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是 ( )
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丁
2.一个四边形顺次添加下列条件中的三个条件便得到正方形:a.两组对边分别相等;b.一组对边平行且相等;c.一组邻边相等;d.一个角是直角.顺次添加的条件:①a→c→d ②b→d→c ③a→b→c.其中正确的是 ( )
A. ①② B. 仅③ C. 仅① D. ②③
3.如图, 在 △ABC 中,∠ACB=90°, BC 的垂直平分线 EF 交 BC 于点D,交 AB 于点 E,且BE= BF,添加一个条件,仍不能证明四边形BECF 为正方形的是 ( )
A. BC=AC B. BD=DF C. AC=BF D. CF⊥BF
第3题图 第4题图
4.如图,AC,BD 是四边形ABCD 的对角线,点E,F分别是AD,BC 的中点,点 M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是 ( )
∥
5.在矩形 ABCD中,M,N,P,Q分别为边 AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下列结论:①存在无数个四边形 MNPQ是平行四边形 ②存在无数个四边形 MNPQ是矩形 ③存在无数个四边形 MNPQ是菱形 ④至少存在一个四边形 MNPQ是正方形.
其中正确结论的序号是 ( )
A. ①③ B. ②③ C. ①②③ D. ①②③④
6.如图,在平行四边形ABCD中,对角线 AC与BD 相交于点E,点 G 为 AD 的中点,连接 CG,CG 的延长线交BA 的延长线于点 F,连接 DF.当 满足__________时,四边形 ACDF 为正方形.
第6题图 第7题图
7.如图,在矩形ABCD中,AC交 BD 于点O,且. 10 cm,将AC绕点C 顺时针旋转 至CE,连接AE,且 F,G分别为AE,EC的中点,则四边形 OFGC 的面积是________.
8.如图,□ABCD的对角线 AC,BD 相交于点 O,且 AE∥BD,BE∥AC,OE=CD.若AD=2,则当四边形ABCD 的形状是_时,四边形 AOBE的面积取得最大值是___________.
第8题图 第9题图
9.已知平行四边形ABCD,对角线AC与BD 相交于点O,点 P在边AD上,过点 P 分别作PE⊥AC,PF⊥BD,垂足分别为点 E,F,PE=PF.
(1)如图,若∠EPF=60°,EO=1,则 PE 的长_____________;
(2)若点 P 是AD的中点,点 F 是DO的中点.则平行四边形 ABCD 是___________形.
10.如图,在Rt△ABC中,∠ABC=90°,BP平分∠ABC 交AC 于点P,过点 P 作 PM⊥AB 于点 M,PN⊥BC 于点N,求证:四边形 BMPN为正方形.
11. 如图,在四边形 ABCD 中, ∥, E是对角线 BD 上一点,且
(1)求证:四边形 ABCD 是菱形;
(2)如果 且 2:3,求证:四边形 ABCD 是正方形.
12.如图1,在正方形 ABCD 中,点 E,F 分别在AB,BC上,且AE=BF.
(1)试探索线段AF,DE的大小关系,写出你的结论并说明理由;
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,顺次连接,得到四边形HIJK.
①请在图2中补全图形;
②四边形 HIJK 是什么特殊平行四边形 请说明理由.
13.如图,在等腰直角三角形ABC中, D是AB 的中点,E,F 分别是AC,BC 上的点(点E 不与端点 A,C重合),且连接 EF 并取EF 的中点O,连接DO并延长至点G,使 连接DE,DF,GE,GF.
(1)求证:四边形 EDFG是正方形;
(2)当点 E 在什么位置时,四边形 EDFG的面积最小 并求四边形 EDFG 面积的最小值.
快乐拓展
14.如图,以△ABC的三边为边在 BC上方分别作等边△ACD,△ABE,△BCF,且点 A 在△BCF 内部.给出下列结论:①四边形ADFE 是平行四边形 ②当AB=AC时,四边形 ADFE 是菱形③当∠BAC=90°时,四边形ADFE 是矩形 ④当AB=AC,且 时,四边形ADFE 是正方形.其中正确结论有__________(填序号).
15.四边形ABCD为正方形,点 E 为对角线AC上一点,连接 DE,BE.过点 E作交射线 BC 于点 F.
(1)如图 1,若点 F 在边 BC 上,求证:
(2)如图 2,以 DE,EF 为邻边作矩形DEFG,连接CG,若 求CG的长度;
(3)若矩形 DEFG 的边 DE 与正方形ABCD一边的夹角是时,直接写出的度数.
参考答案
1. D 2. A 3. C 4. A 5. C
6. AB=AC,∠BAC=90° 8.正方形 2 (2) 正方
10.证明:∵PM⊥AB,PN⊥BC,∴∠PMB=∠PNB=90°,
∵∠ABC=90°,∴四边形 BMPN 是矩形,
∵BP平分∠ABC,PM⊥AB,PN⊥BC,∴PM=PN,∴四边形 BMPN 为正方形.
11.证明:(1)在△ADE与△CDE中,
∴△ADE≌△CDE(SSS),∴∠ADE=∠CDE,
∵AD∥BC,∴∠ADE=∠CBD,∴∠CDE=∠CBD,∴BC=CD,
∵AD=CD,∴BC=AD,∴四边形 ABCD为平行四边形,
∵AD=CD,∴四边形 ABCD 是菱形;
(2)∵BE=BC,∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,
∵四边形 ABCD 是菱形,∴∠ABE=45°,∴∠ABC=90°,∴四边形 ABCD 是正方形.
12.解:(1)AF=DE,理由如下:
∵四边形 ABCD是正方形,∴AD=AB,∠DAE=∠ABF=90°,
∵AE=BF,∴△DAE≌△ABF(SAS),∴AF=DE;
(2)①如图:
②四边形 HIJK 是正方形.理由如下:
∵H,I分别是AE,EF的中点,∴HI是△AEF的中位线, ∥
同理 ∥∴HI=KJ,HI∥KJ,同理 HK=IJ,HK∥IJ,
∵AF=DE,∴HI=KJ=HK=IJ,∴四边形 HIJK 是菱形.
∵△DAE≌△ABF,∴∠ADE=∠BAF,
∵∠ADE+∠AED=90°,∴∠BAF+∠AED=90°,∴∠AOE=90°,
又∵ED∥HK,HI∥AF,∴HK⊥HI,∴∠KHI=90°,
∴四边形 HIJK 是正方形.
13.解:(1)证明:连接CD,如图1所示.
∵△ABC为等腰直角三角形,∠ACB=90°,D是AB 的中点,∴∠A=∠DCF=45°,AD=CD.
在△ADE和△CDF中,∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF.
∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,∴△EDF为等腰直角三角形.
∵OE=OF,OG=OD,∴四边形 EDFG为平行四边形,
∵DE=DF,∴平行四边形 EDFG 为菱形,
∵∠EDF=90°,∴四边形 EDFG 是正方形;
(2)过点 D 作. 于点 如图2所示.
∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC=4,
点 E'为AC的中点,
(点E 与点 重合时取等号).
∴当点 E 为线段 AC 的中点时,四边形EDFG的面积最小,该最小值为4.
14. ①②
15.解:(1)证明:
∵四边形 ABCD 是正方形,AC 为其对角线,∴BC=DC,∠BCE=∠DCE,
∵EC=EC,∴△BCE≌△DCE(SAS),∴∠EBF=∠EDC,BE=DE,
∵四边形 ABCD是正方形,∴∠DCF=90°,
∵DE⊥EF,∴∠DEF=90°,∴∠CDE+∠CFE = 360°-(∠DCF+∠DEF)=180°,
∵∠CFE+∠EFB=180°,∴∠EBF=∠EFB,∴BE=EF,∴DE=EF;
(2)∵四边形 DEFG为矩形,DE=EF,∴四边形 DEFG 为正方形,∴DE=DG,
∵四边形 ABCD 为正方形,∴AD=DC,∠ADC=90°=∠EDG,∴∠ADE=∠CDG,
∴△ADE≌△CDG(SAS),∴AE=CG,
∵AB=4,
(3)当∠ADE=35°时,如图2,
当 时,如图3,
综上所述, 或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
